基于Bayes混合验前分布的成败型产品可靠性评估

张文杰，杨华波2，张士峰2

（1.92853部队，辽宁兴城125109；2.国防科学技术大学航天科学与工程学院，湖南长沙410073）

基于Bayes混合验前分布的成败型产品可靠性评估

张文杰1，2，杨华波2，张士峰2

（1.92853部队，辽宁兴城125109；2.国防科学技术大学航天科学与工程学院，湖南长沙410073）

针对小子样成败型产品可靠性评估问题，引入混合验前分布构造方法，推导了Bayes混合验前分布下成败型产品可靠度参数的验后概率分布函数，研究了验前分布参数对于验后估计的影响，并总结了验前分布参数选择的一般性原则。分析对比了传统Bayes方法和混合验前分布方法的参数验后估计，其结果表明后者能够有效避免验前信息淹没现场信息的问题。对验后均方误差的分析表明混合验前分布方法能够一定程度上改善估计的效果。与幂验前方法的对比结果表明，当验前样本容量较大时，混合验前分布方法的估计效果优于幂验前方法。

系统评估与可行性分析；可靠性评估；成败型；Bayes方法；混合验前分布

0 引言

成败型产品通常是指每次使用都相互独立，并且只有成功或失败两种可能结果的工业品［1］。在可靠性评定领域，涉及到大量的成败型数据［2］，如固体火箭发动机可靠性试验［3］，核电站的应急柴油发动机启动过程［4］。对于一些造价昂贵、危险性高的工业设备，不可能做大量的现场试验进行可靠性评估，这就面临着小子样情况下设备可靠性评估的问题［5］。

Bayes方法是研究小子样问题的一种有效途径，并且在很多领域得到了很好的应用［6］。Bayes方法综合利用验前信息和现场试验信息以实现参数的统计推断［7］。如何合理有效地使用验前信息，是Bayes评定中的关键问题。由于验前信息和现场试验信息并不完全服从同一总体，如果按照经典Bayes方法不加区别地利用验前信息，难免会出现大量的验前信息淹没小样本现场试验信息的情况。为此国内外专家学者进行了一系列研究。Zellner［8］通过引入数据质量因子来描述验前信息和现场试验信息的质量；Ibrahim等［9-10］研究了幂验前分布，并将该方法应用于回归估计中，取得了良好的效果；杨华波等［11］将修正幂验前分布应用于成败型产品的可靠性评估；张士峰等［12］、明志茂等［13］通过引入继承因子，并将继承因子看成随机变量，从而实现可靠性参数的验后统计推断；Helminen［14］则利用Bayes网络来描述不同来源验前信息的差异；杨华波等［15］针对小子样条件下制导精度评定问题，提出了混合验前分布的方法，该方法能够有效避免验前信息“淹没”现场信息的问题。

本文将混合验前分布方法应用于成败型产品的可靠性评估，详细推导了Bayes混合验前分布下产品可靠性参数的验后概率密度函数，研究了混合参数的验前分布参数对于验后估计的影响，并总结了选择这些分布参数的一般性原则，分析了验前信息和现场试验信息的差异对参数验后统计推断的影响。仿真分析表明，与传统的基于似然函数的验前分布构造方法相比，该方法能够有效避免验前信息淹没现场试验信息的问题。对验后均方误差（MSE）的分析表明，混合验前分布方法能够在一定程度上改善Bayes估计的效果。最后将本文所介绍的混合验前分布方法与幂验前分布方法进行比较，当验前样本容量较大时，混合验前分布方法估计效果更好。

1 基于似然函数的验前分布

对某成败型产品进行可靠性试验，其结果服从二项分布B（n，R），其中，n为试验的次数，R为该产品的可靠度。基于Bayes方法的可靠性评估就是综合利用产品的验前信息和现场试验信息实现R的统计推断。假设该产品可靠性试验存在验前信息D0=（n0，s0），现场试验信息D=（n，s），（n0，s0）和（n，s）分别表示验前和现场的可靠性试验次数以及成功的次数，并且D0和D相互独立，L（R|D0）和L（R|D）分别为基于验前信息和现场试验信息的参数R的似然函数，即二项分布的似然函数：

则传统的基于似然函数的验前分布构造方法如下：

式中：π（R）为参数R的初始验前，通常取为无信息验前。则参数R验后分布为

为得到解析的结果，R的无信息验前通常取为二项分布的自然共轭分布：

即

式中：αR、βR为R的验前分布参数；B（αR，βR）为Beta函数。将（1）式、（4）式代入（3）式，并忽略常数项，即可得

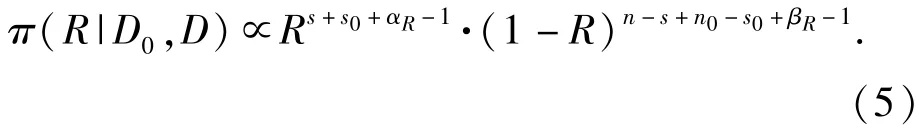
（5）式表明参数R基于似然函数的验后分布仍是Beta分布。根据Beta分布的统计特性，可得R的验后均值为

从参数R的验后表达式（3）式中可看出，这种传统的基于似然函数的验前分布构造方法，实际上是将验前信息D0和现场试验信息D无差别对待，当D0和D不一致或者部分不一致时，上述方法的正确性值得商榷。

通常情况下，验前试验次数n0比现场试验次数n大得多，分析（6）式可知，这种验前信息构造方法，难以避免验前信息“淹没”现场试验信息的问题。

2 混合验前分布

针对上述方法存在的问题，引入混合验前分布

π（R|D0，c）=c·π（R|D0）+（1-c）·π（R），（7）式中：π（R|D0，c）为混合验前分布函数；π（R|D0）为根据验前信息D0而构造的分布函数，对于成败型数据D0=（n0，s0），则为Beta（s0，n0-s0）；混合参数c为验前信息D0与现场试验信息D的相容性，并且满足c∈［0，1］，若c=0，则D0和D不相容；若c= 1，则D0和D完全相容；若0＜c＜1，则D0和D部分相容。

由Bayes公式，可得

将（1）式、（2）式、（4）式、（7）式代入（8）式，并结合Beta分布函数的形式，稍加整理，可得

式中：

通常混合参数c的确定比较困难，本文的做法是将其视为随机变量，并假设参数c的验前分布函数为π（c），由于c∈［0，1］，因此π（c）可以取为Beta（αc，βc），其中，αc、βc为混合参数c的验前分布参数。则（R，c）的联合验后密度函数为

（10）式对R积分，即得混合参数c的验后密度函数

（10）式对c积分，即得可靠度R的验后密度函数

故参数R、c的验后估计可以通过计算各自边缘分布的期望来获得。即

根据Beta分布的统计特性，对（13）式整理得

3 验前分布参数的选择

由（6）式可得传统Bayes方法的可靠度验后估计；由（15）式可得混合验前分布下的验后估计，为方便陈述，称前者为传统方法，后者为混合方法。

在前面的公式推导中分别引入了参数R和c的验前分布参数αR、βR以及αc、βc.由（6）式可以看出，R的验前分布参数αR、βR是有实际物理意义的，因此这里主要研究αc、βc的选择问题，αc、βc的取值影响混合参数c的分布如图1所示。

图1　不同验前分布参数下混合参数c的分布密度函数Fig.1 Distribution density function of hyprid parameter c with respect to different prior distribution parameters

为了说明参数αc、βc对于验后估计的影响，作如下分析：

假设验前信息由二项分布B（n0，p0）抽样得到，现场试验信息由二项分布B（n，p）抽样得到，其中，p0和p分别为验前信息和现场试验信息可靠度真值。令n=10，n0=100，p=0.9，p0=0.5，0.7，0.9，而αc、βc取为不同的组合，仿真5 000次求均值，分别计算传统方法和混合方法的可靠度、混合参数验后估计值计算结果如表1所示。

对比分析表1和图1，不难发现：

1）当验前和现场信息相容性较差时，混合参数c应该适当小一些，这样才能得到更加接近真实值的估计，如p=0.9，p0=0.5，则αc=2，βc=5对应的验后估计0.816 3最接近真实值0.9，因为从图1中可以看到αc=2，βc=5所对应的分布密度曲线的峰值处于（0，0.5）区间之内；相类似地，当验前和现场信息相容性较好时，混合参数c应该适当大一些，如p=0.9，p0=0.9，则αc=5，βc=2对应的验后估计0.884 9最接近真实值0.9，原因就在于αc=5，βc=2在图1中所对应的分布密度曲线的峰值处于（0.5，1）区间之内。

表1　不同验前分布参数下的验后估计结果Tab.1 Results of posteriori estimation with respect to different prior distribution parameters

2）当αc=βc时，从图1中可以看到，其分布密度函数关于直线x=0.5对称，并且只要给定p和p0，无论αc（或者βc）取1还是2，其混合方法的估计值 ^R都相等，而且估计效果介于αc=2、βc=5和αc=5、βc=2之间。

如果已知验前现场信息相容性较好，则应该适当增大βc，使得混合参数c的分布密度函数峰值处于（0.5，1.0）区间；相反，如果验前现场信息相容性较差，则应该适当增大αc，使得混合参数c的分布密度函数峰值处于（0，0.5）区间；如果验前现场信息的相容性并不确定，则应该选择αc=βc，至于具体取何值，这对于可靠性参数的验后点估计 ^R没有影响。

这里给出工程上常见的一种选择方法。参数αc、βc的物理意义不明确，考虑引入Beta分布函数的均值μ∈（0，1）和方差σ2＞0，均值和方差的数值大小反映了验前信息和现场信息的相容程度。验前信息由半实物仿真试验获得，根据半实物仿真系统与实际试验系统的相似程度确定μ和σ2.若二者相似程度很高，则令均值μ取值稍大一些，方差σ2取值稍小一些；相反，若二者相似程度不高，则μ可取小一些，σ2取大一些。如某次半实物仿真试验与现场试验相似程度很高，则令μ=0.8，σ2=0.05.根据Beta分布的统计特性，αc、βc和μ、σ2满足关系式：

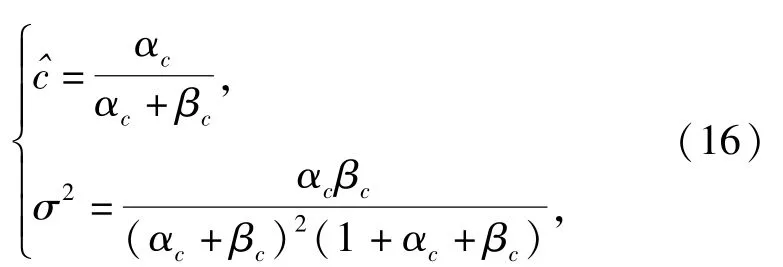
可以反解出αc=1.76，βc=0.44.

4 仿真分析

本文主要研究验前信息和现场试验信息的差异对可靠度R统计推断的影响。事实上，验前信息和现场试验信息的差异主要表现在样本数目和可靠度两个方面，下面分别分析这两种差异对可靠度R验后统计推断的影响。

1）样本容量差异对R统计推断的影响。仿真参数设定为：αR=1，βR=1，αc=1.76，βc=0.44，n= 10，p=0.9，p0=0.4.令n0变化，可以得到传统方法和混合方法下，可靠度R的验后估计随n0的变化情况，如图2所示，图中另一条曲线表示混合方法中参数c的验后估计随n0的变化情况。

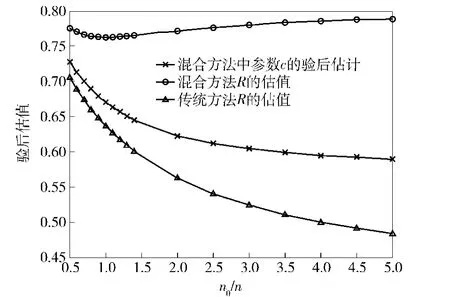
图2　样本容量差异对验后估值的影响Fig.2 Effects of different sample sizes on posteriori estimation

2）可靠度差异对R统计推断的影响。仿真参数设定为：αR=1，βR=1，αc=1.76，βc=0.44，n= 10，p=0.75，n0=100，令p0变化，同样可以得到可靠度R的验后估计随p0的变化情况，如图3所示。

图3　可靠度差异对验后估值的影响Fig.3 Effects of different reliabilities on posterior estimation

分析图2和图3可得到以下结论：

1）图2中，随着n0/n增大，混合方法R的估值始终稳定在0.75～0.80左右（现场信息可靠度真值为0.90），而传统方法R的估值一直减小，由于验前信息的可靠度为0.4，可以预测，如果n0/n继续增大，传统方法 R的估值还会持续减小，最终趋近0.4.这充分说明了混合方法能较好地避免验前信息“淹没”现场试验信息的问题。

2）图3中，横坐标p0-p表示了验前信息和现场试验信息之间的差异。当p0-p为0时，混合方法和传统方法验后估计结果相近，均在0.75（现场信息可靠度真值为0.75）左右，这说明如果验前信息和现场试验信息服从同一总体，则传统方法和混合方法之间的差异并不明显。随着|p0-p|增大，两种方法得到的估值差异变得明显，其中传统方法R的估值基本上和验前信息可靠度真值p0相同，而混合方法R的估值在0.55～0.85之间变化，这也充分说明传统方法不能避免验前信息“淹没”现场试验信息的问题，而混合方法则可以较好地做到这一点。图3中，混合方法中参数c的验后估计曲线解释了混合方法具有这种优势的原因。当|p0-p|=0时达到最大值，即此时相容性最大；随着|p0-p|逐渐增大，c的验后估值减小，于是削弱了验前信息对于R验后估值的影响，因此混合验前分布方法可以有效避免“淹没”问题。

5 MSE分析

前面的分析表明，相对于传统方法而言，混合验前分布方法在一定程度上确实能够避免“淹没”的问题，但是其验后估计特性还需要进一步分析。下面用Monte Carlo仿真方法来分析验后估计的MSE.假设可靠度R的估值为其真值为p，则验后

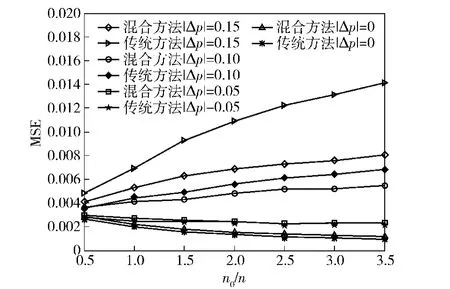
图4　验后MSE分析Fig.4 Analysis of posteriori mean square error

分析图4可以得到以下结论：

1）验后MSE的大小与验前信息的可靠度有关。从图4中可以看到，对于同一种方法而言，当样本容量一定时，|p0-p|越小，其验后MSE就越小，这说明无论是传统方法还是混合验前分布方法，验前信息和现场试验信息可靠度相差越小，其估计效果就越好，反之，估计效果就越差。

2）当|p0-p|=0，0.05时，两种方法的验后估计MSE均随着n0/n的增大而减小；除此之外，其他情况都是随着n0/n的增大而增大。这说明如果验前信息和现场试验信息的可靠度比较接近（例如本次仿真算例中|p0-p|≤0.05），则可以适当增大验前信息的样本容量来改善估计的效果；反之，如果验前信息和现场试验信息的可靠度相差较大（例如本次仿真算例中|p0-p|≥0.1），验前信息样本容量越大，其估计的效果反而变差。该结论与直观上的认识是一致的。

3）当|p0-p|≥0.10时，传统方法的验后MSE普遍大于混合方法的MSE；这说明混合方法确实能够改善估计的效果；而当|p0-p|=0.05时，两种方法的验后MSE基本相当；当|p0-p|=0，传统方法的MSE普遍小于混合方法的MSE，造成上述现象的原因是混合参数c取值不合理，因为上述分析都是在 αc=1.76，βc=0.44的条件下进行的，而当|p0-p|=0时，验前信息和现场试验信息是完全相容的，理想情况下，应该有c=1，根据前面的分析可知，αc应该取较大的值，βc应该取较小的值，在这种情况下，两种方法得到的验后MSE是基本相当的。

美国学者Ibrahim等将幂验前方法应用于线性模型的回归分析［9-10］，同样可以处理验前信息与现场试验信息不完全相容的情况。这里通过一个数值算例，将幂验前方法与本文所介绍的混合方法进行对比。仿真参数设定为：αR=1，βR=1，αc=1.76，βc=0.44，n=10，p=0.9，p0=0.4.令n0变化取值，分别用混合方法和幂验前方法对可靠度R进行估计，结果如图5所示。

图5　两种方法的估计结果Fig.5 Estimated results of hyprid prior and power prior approaches

从图5中可发现，两种方法的估计结果较为接近，均在0.760～0.790之间变化。n0/n＞1.5后，幂验前方法得到的估值趋于稳定；随着n0/n增大，混合方法所得到的估值更接近于现场数据仿真设定的真实值（仿真真值为0.9），即本文所提出的混合方法具有一定的优势。利用相同的仿真设定参数，对这两种方法进行MSE分析，结果如图6所示。

分析图6，当n0/n＜3.0时，幂验前方法的MSE小于混合方法的MSE；当n0/n＞3.0时，幂验前方法的MSE迅速增大，而混合方法的MSE较为平稳。这说明当n0/n较小时，幂验前方法的估计效果优于混合方法，当n0/n＞3.0以后，混合方法的估计效果则优于幂验前方法。

6 结论

本文针对成败型产品可靠性评定的问题，利用混合验前分布的方法构造验前分布，引入混合参数，并根据Bayes方法得到可靠度参数和混合参数的联合概率密度函数，最后通过边缘分布的方法获得混合参数和可靠度参数的验后估计值。研究了混合参数的验前分布参数对于验后估计的影响，并指出了这些分布参数选择的一般性原则。仿真算例表明，与传统Bayes方法相比，混合验前分布方法能够有效避免验前信息“淹没”现场信息的问题。对验后估计的MSE分析表明，本文所提出的混合验前分布方法能够改善估计的效果。与幂验前分布方法的对比结果表明，这两种方法的估计结果相接近，当验前样本容量较大时，本文所提出的混合验前分布方法更具优势。同时也应该注意到该方法的局限性，在最后给出了工程上确定参数αc、βc的方法，但是该方法选择参数μ、σ2需要凭借一定的工程经验，这一不足之处不利于该方法的推广应用，因此如何更加客观合理地选择参数μ、σ2，也就成为了下一步的重点研究方向。

（References）

［1］ 刘晗，郭波.研制阶段的成败型产品可靠性Bayes评估［J］.电子产品可靠性与环境试验，2006，24（5）：25-29. LIU Han，GUO Bo.Bayes assessment for reliability of success or failure product in the development phases［J］.Electronic Product Reliability and Environmental Testing，2006，24（5）：25-29. （in Chinese）

［2］ 张士峰，杨华波，张金槐，等.小样本成败型设备可靠性评估方法［J］.核动力工程，2006，27（5）：79-83.ZHANG Shi-feng，YANG Hua-bo，ZHANG Jin-huai，et al.Reliability assessment methods with small-sample for device with only safe-or-failure pattern［J］.Nuclear Power Engineering，2006，27（5）：79-83.（in Chinese）

［3］ 张士峰，蔡洪.固体火箭发动机性能可靠性评估的Bayes方法［J］.固体火箭技术，2003，26（4）：9-11. ZHANG Shi-feng，CAI Hong.Bayesian approach of performance reliability assessment of solid rocket motors［J］.Journal of Solid Rocket Technology，2003，26（4）：9-11.（in Chinese）

［4］ 茆定远，薛大知.核电站PSA分析中可靠性数据处理的贝叶斯方法［J］.核动力工程，2000，21（5）：451-455. MAO Ding-yuan，XUE Da-zhi.The Bayesian method of data processing in nuclear power plant［J］.Nuclear Power Engineering，2000，21（5）：451-455.（in Chinese）

［5］ 毛昭勇，宋保维，胡海豹，等.基于AMSAA增长模型的鱼雷系统Bayes可靠性分析［J］.兵工学报，2009，30（10）：1401-1404. MAO Zhao-yong，SONG Bao-wei，HU Hai-bao，et al.The Bayes reliability evaluation method based on AMSAA model for torpedo system［J］.Acta Armamentarii，2009，30（10）：1401-1404. （in Chinese）

［6］ 韩明.可靠性工程中参数的E-Bayes估计法及其应用［J］.兵工学报，2009，30（11）：1473-1476. HAN Ming.E-Bayesian estimation method of parameter and its applications in reliability engineering［J］.Acta Armamentarii，2009，30（11）：1473-1476.（in Chinese）

［7］ 谭源源，张春华，陈循，等.基于狄氏先验分布的机电产品主要失效模式贝叶斯分析［J］.兵工学报，2012，33（2）：209-213. TAN Yuan-yuan，ZHANG Chun-hua，CHEN Xun，et al.Bayesian analysis based on dirichlet prior distribution of dominant failure modes for electromechanical products［J］.Acta Armamentarii，2012，33（2）：209-213.（in Chinese）

［8］ Zellner A.Information processing and Bayesian analysis［J］.Journal of Econometrics，2002，107（1）：41-45.

［9］ Ibrahim J G，Chen，M H，Sinha D，et al.On optimality properties of the power prior［J］.Journal of the American Statistical Association，2003，98（1）：204-213.

［10］ Ibrahim J G，Chen M H.Power prior distributions for regression models［J］.Statistical Science，2000，15（1）：46-60.

［11］ 杨华波，张士峰，蔡洪，等.成败型产品可靠性评估的Bayes修正幂验前方法［J］.固体火箭技术，2009，32（2）：131-134. YANG Hua-bo，ZHANG Shi-feng，CAI Hong，et al.Bayesian modified power prior approach for product reliability assessment with only safe-or failure pattern［J］.Journal of Solid Rocket Technology，2009，32（2）：131-134.（in Chinese）

［12］ 张士峰，樊树江，张金槐，等.成败型产品可靠性的Bayes评估［J］.兵工学报，2001，22（2）：238-240. ZHANG Shi-feng，FAN Shu-jiang，ZHANG Jin-huai，et al. Bayesian assessment for product reliability using pass-fail data ［J］.Acta Armamentarii，2001，22（2）：238-240.（in Chinese）

［13］ 明志茂，陶俊勇，陈循，等.基于混合Beta分布的成败型产品Bayes可靠性鉴定试验方案研究［J］.兵工学报，2008，29（2）：204-207. MING Zhi-mao，TAO Jun-yong，CHEN Xun，et al.A Bayes plan of reliability qualification test based on the mixed Beta distribution for success/failure product［J］.Acta Armamentarii，2008，29（2）：204-207.（in Chinese）

［14］ Helminen A.Reliability estimation of safety-critical softwarebased systems using Bayesian networks，STUK-YTO-TR178［R］. Helsinki，Finland：Radiation and Nuclear Safety Authority，2001.

［15］ 杨华波，蔡洪，张士峰，等.基于混合验前分布的制导精度评定方法［J］.航空学报，2009，30（5）：855-860. YANG Hua-bo，CAI Hong，ZHANG Shi-feng，et al.Evaluation of missile guidance precision based on hybrid prior distribution ［J］.Acta Aeronautica et Astronautica Sinica，2009，30（5）：855-860.（in Chinese）

Reliability Assessment for Device with Only Safe-or-failure Pattern Based on Bayesian Hyprid Prior Approach

ZHANG Wen-jie1，2，YANG Hua-bo2，ZHANG Shi-feng2
（1.Unit 92853 of PLA，Xingcheng 125109，Liaoning，China；2.School of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，Hunan，China）

For the reliability evaluation of device with only safe-or-failure pattern，a hyprid prior approach is introduced，and the posteriori probability distribution function of reliability parameter is deduced by Bayesian method.The influence of prior distribution parameters on the posterior estimation is considered，and the general rules of choosing these parameters are summarized.The parameter posterior estimates of traditional Bayesian method and hyprid prior approach are compared.The results indicate that the hyprid prior approach can avoid the problem of that the prior data inundate the posteriori data effectively.The analysis of posteriori mean square error demonstrates that the hyprid prior approach can improve the performance of estimation to some extent.Through the comparison with power prior approach，it is proved that the estimation effect of hyprid prior approach is better than that of power prior approach，especially when prior sample size is larger.

system assessment and feasibility analysis；reliability assessment；safe-or-failure pattern；Bayesian method；hyprid prior approach

TB114.3

A

1000-1093（2016）03-0505-07

10.3969/j.issn.1000-1093.2016.03.016

2015-03-22

张文杰（1991—），男，硕士研究生。E-mail：zhangwenjie_0731@163.com；张士峰（1971—），男，教授，博士生导师。E-mail：zhang_shifeng@hotmail.com