未知包络多分量线性调频脉冲信号参数估计

徐舟，张浩，程水英

（电子工程学院雷达对抗系，安徽合肥230000）

未知包络多分量线性调频脉冲信号参数估计

徐舟，张浩，程水英

（电子工程学院雷达对抗系，安徽合肥230000）

针对雷达侦察中的未知包络线性调频（LFM）信号参数估计问题，基于时频分析与相干积累，提出了脉冲数、调频率、中心频率、时延和脉宽参数的估计方法。利用时频分析对脉冲数与调频率进行粗估计，结合分数阶傅里叶变换（FRFT）完成脉冲数与调频率精估计；进行局部相干积累，提取中心频率、时延和脉宽。仿真分析表明：多分量LFM信号中的强脉冲可能对弱脉冲信号的参数估计产生干扰。针对该问题，在FRFT域对强脉冲进行了遮蔽处理。推导了估计参数的克拉美劳下界，并对估计误差进行了分析，结果表明：对于多分量LFM脉冲信号，遮蔽强脉冲信号后，弱脉冲信号的脉宽估计精度可显著提高。

雷达工程；多分量线性调频信号参数估计；时频分析；分数阶傅里叶变换；克拉美劳下界

0 引言

线性调频（LFM）信号能够利用大的时宽和带宽积，获得距离高分辨，在通信、雷达等微波领域具有广泛的应用，LFM信号的参数估计是一个重要的研究课题［1-2］。

目前，多分量LFM信号参数估计方法主要有：基于时频分布直线提取的参数估计方法［3-4］（如Radon-Ambiguity变换，Wigner-Hough变换），基于分数阶傅里叶变换［5-7］（FRFT）的参数估计方法。基于时频分布直线提取的参数估计方法主要利用LFM信号在时频图中的直线特征，直线的斜率对应信号的调频率，通过估计时频图中直线的斜率完成对信号调频率的估计。常用的时频变换有短时傅里叶变换［8］（STFT）、Wigner-Ville变换（或模糊函数）［9］，STFT为一次时频变换，计算速度快，但是时频分辨率受到Heisenberg测不准原理的限制，估计精度受限，Wigner-Ville分布精度较高，但是存在交叉项干扰问题。FRFT通过旋转频率空间，在特定阶次上聚集LFM信号的能量，等价于脉冲压缩，参数估计精度高，但是FRFT需要进行二维谱峰搜索，计算量较大。文献［10］提出了基于Radon-Ambiguity变换和FRFT的谱校正参数估计方法，将二维搜索问题转化为了两次一维搜索问题。文献［11］将离散多项式变换与FRFT相结合对加速运动的目标进行检测，其本质也是LFM信号的检测与估计问题。对于多分量信号而言，其参数估计问题一般按照信号能量的强弱依次提取并进行估计。

纵观以上方法，多分量LFM信号参数估计问题主要集中在已知基带信号的调制参数估计。然而，在实际的电子侦察系统中，脉冲信号的上升沿、下降沿、脉宽、到达时间等参数是不完全已知的，也就是说信号的包络是未知的。对于电子侦察系统，信号脉宽、到达时间等参数同样需要进行估计［12-14］，在该条件下，以上LFM参数估计方法或者无法使用，或者搜索维数急剧增大，效率大幅度降低。鉴于此，本文对未知包络多分量LFM脉冲信号的参数估计问题展开研究，推导了信号调频率、中心频率、脉冲时延和脉宽参数估计子，并分析了估计误差，具有一定的实用价值。

1 未知包络LFM脉冲信号时频域检测

1.1未知包络LFM脉冲信号模型

在电子侦察系统中，脉冲调制LFM信号模型可以表示为式中：N为脉冲数目；Ai为第i个脉冲的幅度为第i个脉冲的时间延迟为第i个脉冲的中心频率；ki为第i个脉冲的调频率；w（t）是高斯复噪声；pi（·）为第i个脉冲的实包络。图1给出了信号包络及相关参数示意图。

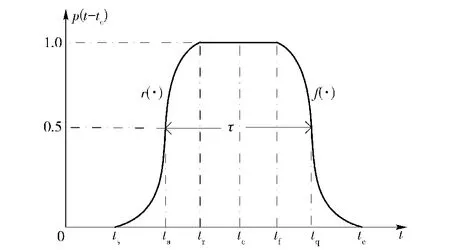
图1　脉冲包络示意图Fig.1 Pulse envelope

图1中：r（·）、f（·）分别表示脉冲的上升沿与下降沿；ts为脉冲起始时刻；ta为脉冲上升到0.5的时刻（通常该时刻称为脉冲到达时刻）；tr为脉冲幅度饱和时刻；tc为脉冲时延；tf为脉冲下降时刻；tq为脉冲下降到0.5的时刻；te为脉冲结束时刻。脉冲宽度τ=tq-ta.本文假定r（·）、f（·）关于中心时刻对称。

1.2STFT时频域检测

为更好地估计LFM信号参数，首先需要对信号中包含的脉冲进行检测并估计脉冲数目。LFM脉冲信号在时频域上具有有限支集，而噪声在整个时频域均有分布，因此在二维时频域检测信号更加合适。考虑到信号交叉项干扰与运算速度问题，本文在STFT域对信号进行检测［15］，信号s［n］的离散STFT 定义为

式中：L为采样点数；g［n］为离散窗函数；m、l为二维时频图中的位置。

记H0假设为信号中仅包含噪声，H1假设为信号中同时包含噪声与感兴趣信号。H0条件下，

式中：Re｛·｝和Im｛·｝分别表示复数的实部和虚部。设Re｛w［n］｝、Im｛w［n］｝是0均值、方差为σ2的高斯白噪声且相互独立，Re｛Gs［m，l］｝和Im｛Gs［m，l］｝是Re｛w［n］｝与Im｛w［n］｝的线性变换，因此Re｛Gs［m，l］｝和Im｛Gs［m，l］｝均服从高斯分布且实部与虚部相互独立。

通常情况下，g［n］具有单位能量。统计量|Gs［m，l］|服从瑞利分布：

得时频域判决表达式

式中：Q1为虚警率所确定的门限，可由瑞利分布的分位点计算得到。

2 LFM脉冲参数估计

2.1脉冲数与调频率估计

2.1.1脉冲数与调频率粗估计

经时频域检测后，时频图 Gs［m，l］二值化为时频图的二值化可减小信号幅度对脉冲数目提取的影响。信号在二值时频图中表现为直线线段，记H［θ，ρ］为的Hough变换，提取H［θ，ρ］的局部谱峰完成脉冲数和调频率粗估计，局部谱峰的判决表达式如下：

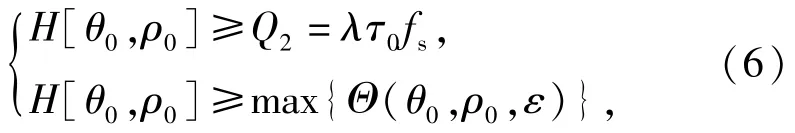
式中：Q2为阈值；λ为不超过1的系数；τ0为脉冲信号的脉宽粗略值；fs为离散采样率；Θ（θ0，ρ0，ε）为以（θ0，ρ0）为中心的ε邻域，受到STFT分辨率的影响，高于阈值的点可能比较多，因此需要进行局部极大值判断。根据峰值数目和位置获得脉冲数与调频率的粗估计

2.1.2脉冲数与调频率精估计

FRFT是傅里叶变换的广义形式，它在统一的时频域上进行信号处理。对于LFM信号，其最佳阶次的FRFT相当于脉冲压缩，具有输出信噪比高、稳健性好等优点。对于给定的LFM脉冲信号，

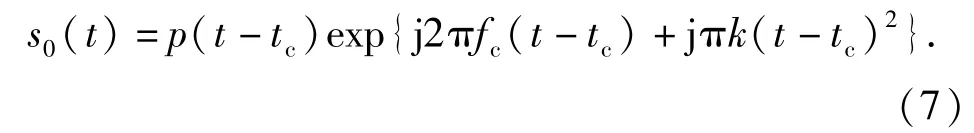
其最佳变换阶次为α0=-acot（k），FRFT模值［7］表示为

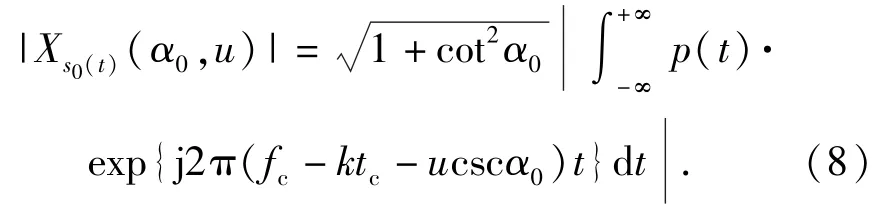
（8）式表明，无论信号包络 p（t）的形式如何，|Xs0（t）（α，u）|在（α0，u0）处获得谱峰，且

（9）式第一个分式确定了LFM信号调频率的估计值，第二个分式确定了信号的时频关系。

STFT的时频分辨率受到Heisenberg测不准原理的限制，因此需要使用FRFT对脉冲数与调频率进行精估计。以脉冲数与调频率的粗略估计值为先验，在其邻域内进行FRFT并对谱峰进行搜索，记录谱峰位置，获得调频率的精估计。若存在两个以上的脉冲谱峰位置一致，则认为粗估计中存在重复脉冲，对重复脉冲进行剔除。

综合以上分析，LFM脉冲数与调频率精估计步骤归纳于表1中。

表1　脉冲数与调频率精估计处理步骤Tab.1 Processing steps for fine estimation of pulse number and frequency modulation rate

2.2脉冲时延与中心频率估计

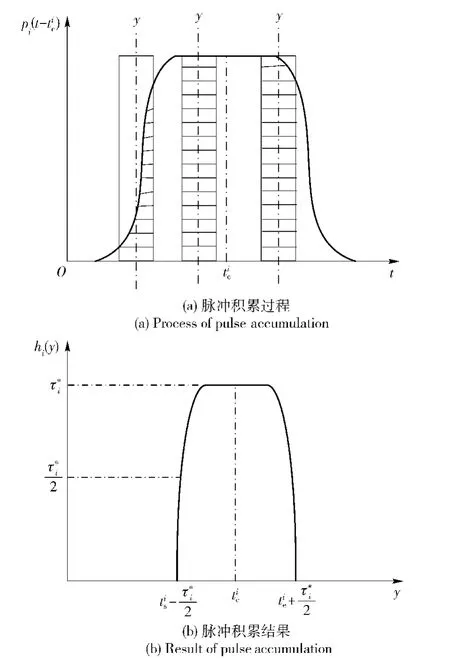
图2　脉冲积累示意图Fig.2 Accumulation of pulse

鉴于以上分析，只要脉冲包络的上升沿与下降沿是对称的，或者近似对称的，无论其具体函数形式如何，脉冲积累函数hi（y）的自相关函数在处获得最大值。因此，脉冲时延与中心频率估计子可表示为

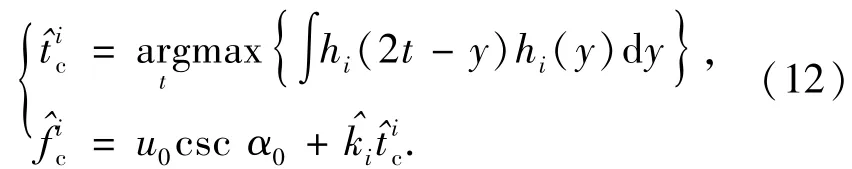
2.3脉冲宽度估计

提取hi（y）的左半部分hi（y）与右半部分h+i（y），其自相关分别表示为

式中：

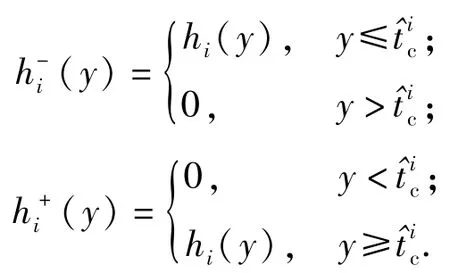
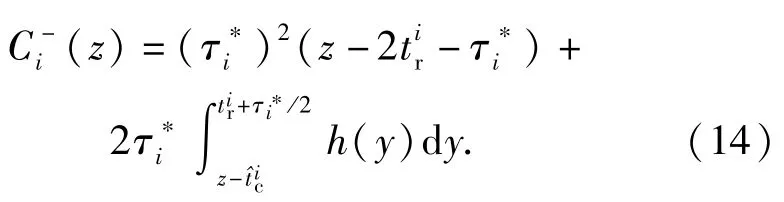
对自变量求微分并令其等于0，得

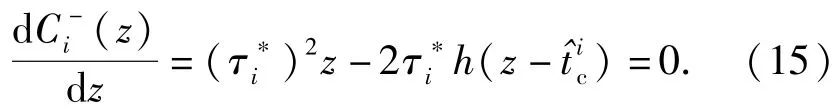
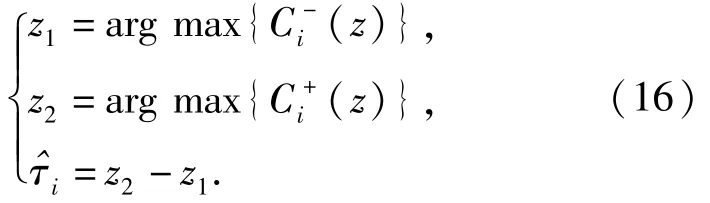
（16）式表明，只要时延估计误差不超出hi（y）的稳定最大值范围内，则脉宽的估计与时延无关。

3 仿真实验与误差分析

3.1仿真实验

图3（a）仿真了3个幅度为［0.5 mV，0.7 mV，1.0mV］，时延为［4 μs，8 μs，15 μs］的LFM脉冲信号，包络函数由以下表达式确定，中心频率为［20 MHz，30 MHz，10 MHz］，调频率为［3.0 MHz/μs，5.0 MHz/μs，1.0 MHz/μs］，采样率设置100 MHz；图3（b）为加噪声的信号，噪声方差为0.5，对应信噪比为［-3 dB，0 dB，3 dB］.

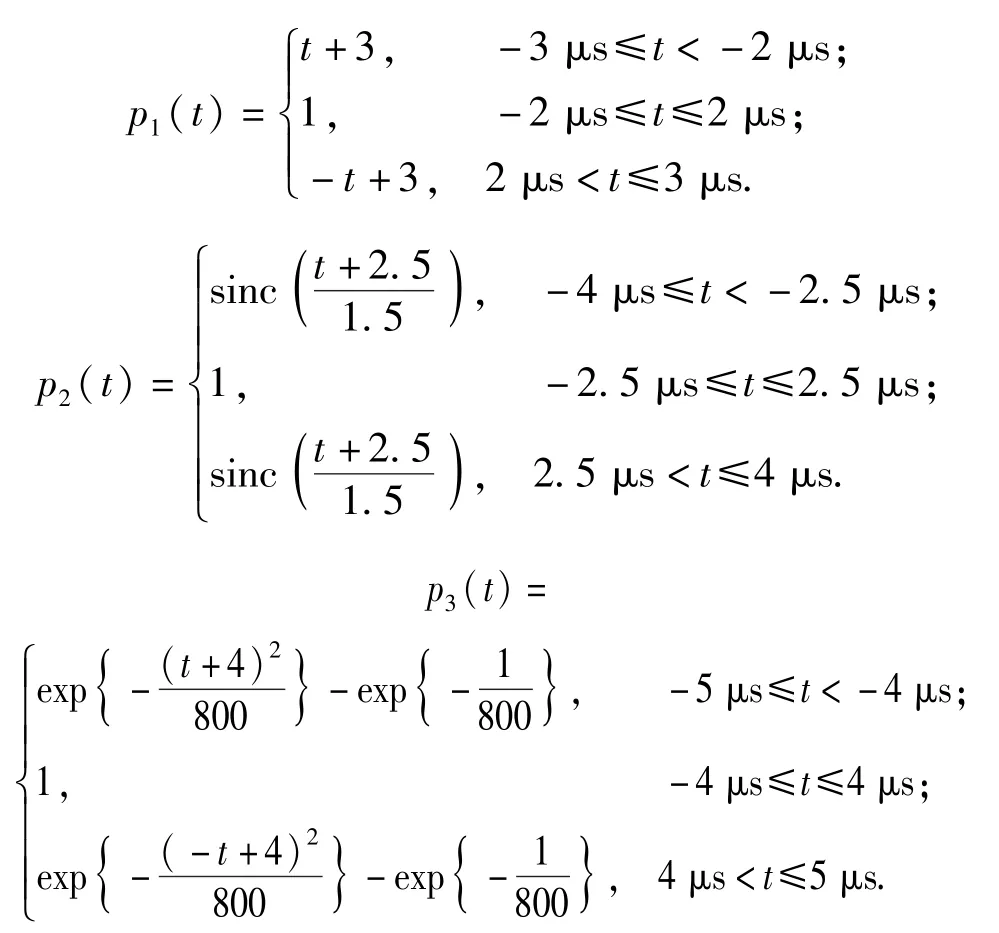
图3　多分量LFM脉冲信号仿真Fig.3 Simulation of multicomponent LFM signal

图4（a）和图4（b）给出了信号的STFT检测，窗函数设置为高斯型，窗长55个采样点，虚警率设定为0.05；对二值时频图进行Hough变换，完成脉冲数目与调频率的粗估计，一般情况下，LFM脉冲信号的脉宽均会大于5 μs，因此将λ设定为0.8，τ0设定为5 μs；对脉冲数与调频率进行精估计，结果列于表2中。

图4　多分量LFM脉冲检测Fig.3 Detection of multicomponent LFM signal

表2　FRFT调频率与时频关系精估计参数表Tab.2 FRFT fine estimation of pulse number and frequency modulation rate

研究发现，脉冲数目和调频率估计会对后续参数估计产生较大影响。虽然精估计能够提高调频率估计精度并剔除重复脉冲。但是粗估计中发生的漏检问题无法恢复，因此在粗估计过程中可将Q2取得略小一些，防止漏检。STFT变换的窗长应该适中选取，当窗长较小时，频率分辨率低，杂波在频率域上发生了扩展，不利于时频图的二值化与脉冲数目估计；而窗长过大时，时域分辨率低，容易导致时频图中的直线在时间域上产生模糊，也不利于参数估计，经仿真研究STFT窗长设置为0.4～0.6 μs较为合适。

从二值时频图中提取满足时频关系的线段，为防止小信噪比情况下漏警造成线段开裂，在提取之前先对时频图做形态学膨胀处理。取图5给出了对应的局部积累曲线

图5　脉冲积累曲线Fig.5 Pulse accumulation curve

从图5中不难看出，积累曲线的幅度和平坦度受到信噪比的影响。总的趋势是信噪比越高，累积曲线的幅度越大且平坦度越好。从这个意义上讲，大信噪比有利于提高参数估计精度，表3列出了各个脉冲参数的估计值与真实值以供对比。

表3　参数估计值与真实值对比表Tab.3 Comparison of estimation value and true value

表3中数据显示：对于信噪比为3 dB的脉冲，调频率、中心频率、中心时刻、脉宽均具有较高的估计精度；对于信噪比-3 dB、0 dB的脉冲，除调频率参数估计较为准确外，其余参数均产生了一定的误差，尤其是脉冲宽度偏差较大。仔细分析，主要原因有两点：其一，脉冲信号的信噪比较低，导致了参数估计的均方误差增大，误差起伏增加；其二，强脉冲信号能量泄漏至弱脉冲，导致弱脉冲的积累曲线产生偏差。从时频图4（a）中看出，调频率为5.0 MHz/μs的信号（2号脉冲，信噪比0 dB）邻近脉冲结束处与调频率为1.0 MHz/μs的信号（3号脉冲，信噪比3 dB）在时频域内存在交叠，与调频率为3.0 MHz/μs （1号脉冲，信噪比-3 dB）的信号在时域内存在交叠，由于3号脉冲能量较强，直接导致了2号脉冲的中心频率与中心时刻估计值向右偏移，脉冲宽度估计值增大。

为克服强脉冲干扰弱脉冲的现象，参照文献［7］方法，在弱脉冲相干积累之前，在FRFT域对强脉冲做遮蔽处理，然后将信号变换回时域对弱脉冲参数进行估计。图6给出了强脉冲遮蔽后的积累曲线，表4列出了强脉冲遮蔽后的LFM参数估计值与真实值以供对比。

从图6中曲线看出：1号脉冲的积累曲线也变得相对平坦，但是由于信噪比较低，仍然存在一定的起伏；2号脉冲积累曲线的下降沿更加平滑，受到强脉冲的干扰降低。从表4中数据看出，因为调频率估计是在强脉冲遮蔽处理之前，因此调频率估计值没有变化，而强脉冲遮蔽后，1号脉冲、2号脉冲的中心频率、中心时刻、脉宽参数的估计误差显著下降。

3.2误差分析

3.1节对LFM脉冲信号的参数估计进行了仿真实验，本节主要对参数估计的精度进行分析。首先推导信号参数估计的克拉美劳下界（CRLB）［16-17］。

图6　脉冲积累曲线（强脉冲遮蔽）Fig.6 Pulse accumulation curve（strong pulse filtering）

表4　LFM脉冲参数估计值与真实值对比表（强脉冲遮蔽）Tab.4 Comparison of estimation value and true value（strong pulse filtering）

记信号观测向量x=［x［1］，x［2］，…，x［L-1］］T，估计参数集ξ=［fc，k，nc，τ］T，分别对应信号的中心频率、调频率、时延和脉宽，对数似然函数：

式中：s0［n］为信号s0（t）的离散采样。计算Fisher信息阵，进而得到参数估计的CRLB：

采用蒙特卡洛实验绘制参数估计的均方误差曲线。仿真幅度参数设置A3=0，A2=2A1，其余参数与3.1节一致。图7以1号脉冲（梯形上升沿）为例绘制了不同信噪比条件下参数估计的均方根误差曲线。

从图7中看出，随着信噪比的增大，参数估计的均方误差呈下降趋势。调频率参数的估计精度几乎达到CRLB，这是因为FRFT能够获得高的峰值信噪比，稳健性较好。然而，其他估计参数的均方误差与CRLB仍然存在一定的距离，原因有两个：1）参数的估计不是独立的，调频率的估计误差会导致脉冲积累失配，直接影响到中心频率、时延、脉宽参数的估计精度；2）中心频率、时延、脉宽参数估计时只对脉冲进行了部分相干积累，峰值信噪比较低，导致了较大的偏差。图7中曲线显示，在调频率存在一定区分的条件下，强脉冲对弱脉冲的调频率、中心频率、中心时刻参数估计影响较小，而对脉宽参数估计的影响较大。当对强脉冲进行遮掩后，脉宽参数的估计精度显著提高。

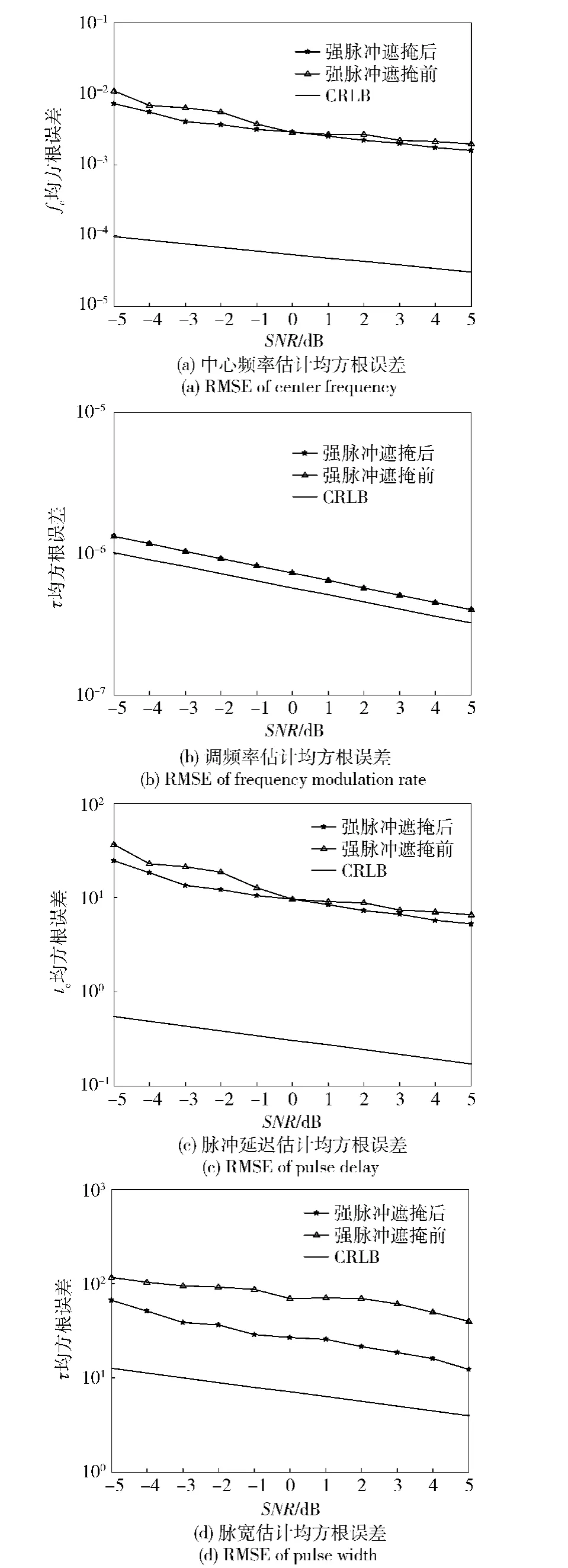
图7　不同信噪比下参数估计的均方根误差曲线Fig.7 RMSEs of parameter estimation under different SNRs

4 结论

实际遇到的雷达侦察问题，脉冲到达时间、脉冲包络等参数均是未知的。本文提出了未知包络多分量LFM脉冲信号参数估计方法，特别适用于对LFM脉冲雷达的侦察，并得出以下结论：

1）对于中心频率、调频率、到达时间均未知的LFM脉冲，FRFT能够较好地估计信号的调频率，但是无法准确估计中心频率与到达时间。

2）对于“钟形”包络脉冲，利用局部自相关方法可以较好地估计中心频率、到达时间、脉宽等参数，并具有稳健性。

3）在利用局部自相关方法进行参数估计时，时频域相邻较近的强信号容易对弱信号产生影响，进行强脉冲抑制后可提高估计精度。

（References）

［1］ Zaugg E C，Long D G.Generalized frequency scaling and backprojection for LFM-CW SAR processing［J］.IEEE Transactions on Geoscience and Remote Sensing，2015，53（7）：3600-3614.

［2］ Su J，Tao H，Rao X，et al.Coherently integrated cubic phase function for multiple LFM signals analysis［J］.Electronics Letters，2015，51（5）：411-413.

［3］ Zhang Z，Luo M.New integral transforms for generalizing the Wigner distribution and ambiguity function［J］.IEEE Signal Processing Letters，2015，22（4）：460-464.

［4］ Li Y，Xiao X.Recursive filtering Radon-ambiguity transform algorithm for detecting multi-LFM signals［J］.Journal of Electronics （China），2003，20（3）：161-166.

［5］ Cowell D M J，Freear S.Separation of overlapping linear frequency modulated（LFM）signals using the fractional Fourier transform ［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2010，57（10）：2324-2333.

［6］ 王瑞，马艳.基于分数阶傅里叶变换的线性调频脉冲信号波达方向估计［J］.兵工学报，2014，35（3）：422-427. WANG Rui，MA Yan.DOA estimation of wideband linear frequency modulated pulse signals based on fractional fourier transform［J］.Acta Armamentarii，2014，35（3）：422-427.（in Chinese）

［7］ Qi L，Tao R，Zhou S，et al.Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform［J］.Science in China Series F：Information Sciences，2004，47（2）：184-198.

［8］ Pei S C，Huang S G.STFT with adaptive window width based on the chirp rate［J］.IEEE Transactions on Signal Processing，2012，60（8）：4065-4080.

［9］ Pei S C，Ding J J.Fractional Fourier transform，Wigner distribution，and filter design for stationary and nonstationary random processes［J］.IEEE Transactions on Signal Processing，2010，58（8）：4079-4092.

［10］ 罗蓬，刘开华，黄翔东，等.高精度LFM信号参数估计的谱校正方法［J］.系统工程与电子技术，2011，33（6）：1237-1242. LUO Peng，LIU Kai-hua，HUANG Xiang-dong，et al.High-accuracy parameter estimation for LFM signals based on spectrum correction［J］.Systems Engineering and Electronics，2011，33（6）：1237-1242.（in Chinese）

［11］ 庞存锁.基于离散多项式相位变换和分数阶傅里叶变换的加速目标检测算法［J］.电子学报，2012，40（1）：184-188. PANG Cun-suo.An accelerating target detection algorithm based on DPT and fractional Fourier transform［J］.Acta Electronic Sinica，2012，40（1）：184-188.（in Chinese）

［12］ Yu J，Zhang L，Liu K.Coherently distributed wideband LFM source localization［J］.IEEE Signal Processing Letters，2015，22（4）：504-508.

［13］ Chan Y T，Lee B H，Inkol R，et al.Estimation of pulse parameters by sutoconvolution and least squares［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（1）：363-374.

［14］ 邓兵，王旭，陶然，等.基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析［J］.兵工学报，2012，33（6）：764-768. DENG Bing，WANG Xu，TAO Ran，et al.Performance analysis of time delay estimation for linear frequency-modulated pulse based on fractional Fourier transform［J］.Acta Armamentarii，2012，33（6）：764-768.（in Chinese）

［15］ Duan Y，Wang J Z，Su S Y，et al.Detection of LFM signals in low SNR based on STFT and wavelet denoising［C］∥IEEE 2014 International Conference on Audio，Language and Image Processing（ICALIP）.Shanghai，China：IEEE，2014：921-925.

［16］ Peleg S，Porat B.The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase［J］.IEEE Transactions on Signal Processing，1991，39（3）：749-752.

［17］ Ristic B，Boashash B.Comments on“the Cramer-Rao lower bounds for signals with constant amplitude and polynomial phase”［J］.IEEE Transactions on Signal Processing，1998，46（6）：1708-1709.

Parameter Estimation of Unknown Envelope Multicomponent LFM Signal

XU Zhou，ZHANG Hao，CHENG Shui-ying
（Department of Radar Countermeasures，Electronic Engineering Institute，Hefei 230000，Anhui，China）

For the estimation of unknown envelope multicomponent linear frequency modulation（LFM）signal in radar reconnaissance，the methods for the estimation of pulse number，frequency modulation rate，center frequency，delay and pulse width are proposed based on time-frequency analysis and coherent accumulation.A rough estimation is done for the parameters of pulse number as well as frequency modulation rate by time-frequency analysis，after which a fine estimation is conducted based on fractional Fourier transform（FRFT）.Then some parameters，such as center pulse，delay and pulse width，can be extracted by coherent accumulation.Simulation results show that the weak pulse parameters estimation may be affected by strong pulse，which can be solved by filtering in FRFT domain.At last，Cramer-Rao low bounds of parameters are derived，and the estimation errors of parameters are analyzed.Results show that the estimation accuracy of width of weak pulse can be improved significantly after strong pulse filtering.

radar engineering；multicomponent linear frequency modulation signal parameter estimation；time-frequency analysis；fractional Fourier transform；Cramer-Rao low bound

TN911

A

1000-1093（2016）03-0462-09

10.3969/j.issn.1000-1093.2016.03.011

2015-07-09

国家自然科学基金项目（61201379）

徐舟（1990—），男，助教，硕士。E-mail：zhouzhou900521@126.com；张浩（1986—），男，讲师，硕士。E-mail：zhang-g03@163.com