旋转矢量在高动态全姿态飞行器运动方程中的应用
王红辉,杨绍卿1,吴成富2,郝峰1,车晓涛1
(1.西安现代控制技术研究所,陕西西安710065;2.西北工业大学自动化学院,陕西西安710072)
旋转矢量在高动态全姿态飞行器运动方程中的应用
王红辉1,2,杨绍卿1,吴成富2,郝峰1,车晓涛1
(1.西安现代控制技术研究所,陕西西安710065;2.西北工业大学自动化学院,陕西西安710072)
基于旋转矢量是表示角位置变化所对应的等效旋转而不是角位置本身这一基本思想,同时借鉴旋转矢量在捷联惯性导航算法中的应用,建立了将旋转矢量应用于高动态全姿态飞行器运动方程的数学框架。既克服了欧拉角法不适于全姿态解算的缺点,同时,相比于四元数法又提高了高动态角运动情况下姿态解算的效率。对旋转矢量法、四元数法和欧拉角法在数值解算中的不可交换误差进行了分析。据此,针对单通道具有高动态特性的轴对称飞行器,建立了基于准弹体系的旋转矢量法,提高了解算效率。基于某型滚转导弹运动方程的数字仿真表明了旋转矢量法在姿态解算中的有效性和广泛性。
飞行器控制、导航技术;旋转矢量;欧拉角;四元数;高动态;全姿态
0 引言
飞行器运动方程是表征飞行器运动规律的数学模型。对飞行器运动方程进行快速精确的数值解算,具有重要的理论和应用价值。其中,姿态解算是整个运动方程解算中十分重要的一环。
在飞行器的运动姿态解算中,常用的有欧拉角法和四元数法[1-2]。任意转动都可通过坐标轴的连续3次旋转来描述,这3个转角就形成了一组欧拉角[3]。关于欧拉角的转动次序,科学界尚未达成统一,对3次连续转动的唯一约束为两次相邻转动轴不能是同一个坐标轴。据此,欧拉角共有12种合法定义[4]。欧拉角在姿态描述中的优点是物理意义明确,但是在某些角度会出现运动学奇点。对不同的欧拉角转动次序,出现的奇点会有所不同,因此,欧拉角不适于全姿态的解算。四元数是在19世纪中期由爱尔兰数学家Hamilton引入数学中的,直到20世纪60年代才被应用于姿态解算中[5]。四元数在姿态解算中的优点是不会出现奇点,且四元数的运算律适于进行姿态解算。四元数的缺点是其4个参数的物理意义不明确,用于描述转动的4个参数必须满足归一化条件[6-7]。但是,在姿态数值解算过程中,这种归一化条件将会丧失,从而需要重新进行归一化[8-9]。这说明四元数在姿态解算中存在明显的归一化误差。同时,在刚体做有限转动时,刚体的空间角位置与旋转次序有关,即在姿态解算中存在旋转的不可交换性误差。龙格-库塔法是飞行器运动微分方程比较常用的一种数值解法。四元数的龙格-库塔法实际上相当于四元数毕卡算法的有限阶近似,本文将对此予以分析。但四元数的毕卡算法仅为单子样算法,数值解算的不可交换性误差较大,尤其在高动态环境中,这种不可交换性误差将更加严重[7]。为了提高四元数解算的精度,只能通过降低数值解算的步长来减小算法误差。
除了欧拉角法和四元数算法外,可用于姿态解算的还有方向余弦矩阵法、罗德里格参数(或称为吉布斯矢量)法[10-12]、等效旋转矢量法[13-15]等。方向余弦矩阵可以根据两个坐标系之间夹角的余弦定义,也可根据一个坐标的基矢量在另一个坐标的投影来定义[3,16]。因此,方向余弦矩阵的优点是物理意义明确,但其缺点是在求解时待定参数较多,并且存在正交归一化误差。罗德里格参数实质上是四元数在三维超平面上的投影,它去除了四元数的一个冗余度,因此存在和四元数同样的误差,同时在某些角度也会出现奇异性。等效旋转矢量的概念由Bortz和Jordan于1971年提出[13,17-18]。Bortz根据方向余弦矩阵和旋转矢量的解析关系,严格推导了旋转矢量所满足的微分方程,得出旋转矢量的微分等于角速度加上非交换误差项,从而将由旋转的不可交换性引入的姿态误差分离了出来。Bortz的工作为姿态解算的不可交换性误差的分析和校正提供了严格的理论基础。
等效旋转矢量可由坐标系内的一个方向及坐标系在该方向上的旋转角度定义,它表征不同时刻角位置变化所对应的一次性等效旋转而不反映其中间过程。由于旋转矢量对不可交换性误差的分离,它在适于高动态角运动的捷联惯性导航算法中应用广泛[14,19-25]。旋转矢量和欧拉角、罗德里格参数一样,均为姿态的三维参数化表示,可表示任意姿态。Stuelpnagel从三维转动群的角度表明姿态的三维参数化表示无法同时满足全局性和非奇异性[26]。因此,Bortz方程在某些角度同样呈现出奇异性。这影响了它在全姿态飞行器运动方程中的直接应用。目前,尚没有公开的文献对旋转矢量在飞行器运动方程中的数值解算进行过详细的研究。
基于旋转矢量是表示角位置变化所对应的等效旋转而不是角位置本身这一基本思想,同时借鉴旋转矢量在捷联惯性导航算法中的应用,本文建立了将旋转矢量应用于高动态全姿态飞行器运动方程的数学框架。其基本思想是把姿态信息以不具有奇异性的四元数的形式表示,把姿态变化信息以旋转矢量的形式表示。在每次数值解算之后,把姿态变化信息从旋转矢量的表示中转移到四元数的表示中。如此,旋转矢量在每次数值解算更新之前始终为0,而更新之后始终是一个小量,从而远离其运动学奇点。同时,由于旋转矢量是姿态的无约束表示,在整个计算过程中,四元数能够始终满足归一化条件。这样,既克服了欧拉角和四元数算法的缺点,又保留了其优点。基于某型滚转导弹运动方程的数字仿真验证了该算法的有效性。对于非全姿态运动的情况,本文详细分析了欧拉角法和旋转矢量算法的不可交换性误差,指出了在某些特定情况下欧拉角法比旋转矢量算法解算精度偏高的原因。据此,针对轴对称飞行器(如滚转导弹),建立了在单通道高动态情况下应用旋转矢量的数学框架,从而使得旋转矢量法取得了和欧拉角法相当的解算精度。
1 坐标系定义和符号约定
为便于分析,本文运动方程的建立采用平板地球假设,即不考虑地球曲率的影响。
地面坐标系(g系):地面坐标系与地球固连,坐标原点位于发射点,x轴与发射点和目标连线重合,指向目标为正;y轴沿地垂线,指天为正;z轴按右手定则来确定。
弹体坐标系(b系):坐标原点位于导弹的质心,x轴与弹纵轴方向一致,指向头部为正;对于轴对称型导弹,其余两轴与弹体固联。对于面对称型,y轴位于弹体纵向对称面内与x轴垂直,指向上为正,z轴按右手定则来确定。
准弹体坐标系(q系):坐标原点位于导弹的质心,x轴与弹纵轴方向一致,指向头部为正;y轴在铅垂面内,通过原点O垂直于x轴,指向上方为正;z轴按右手定则来确定。
在上述坐标系定义下,弹体姿态欧拉角(ψ,ϑ,γ)采用yzx的转动次序。单位四元数q记为q= (q0,q1,q2,q3)T,qv=(q1,q2,q3)T为矢量部分,q0为标量部分。q的共轭为q*=(q0,-q1,-q2,-q3)T,其逆为q-1=q*.四元数p和q的乘法满足

或

对于任一矢量u,定义p=(0,u),则有
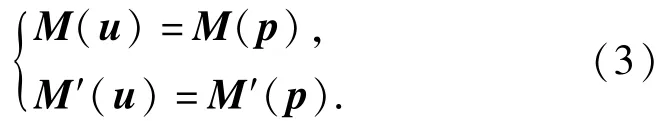
在上述定义下,欧拉角(ψ,ϑ,γ)可根据姿态四元数q计算如下:

矢量u和v的叉乘可写为
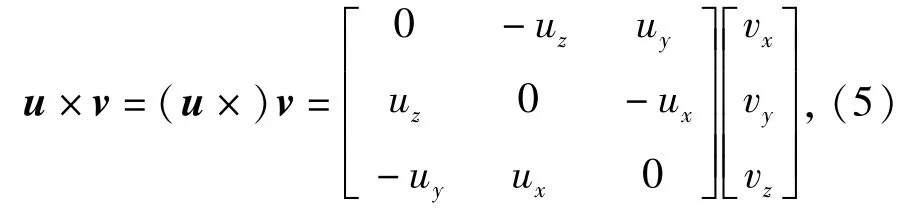
式中:(u×)为矢量u的斜对称矩阵。
任意两个坐标系的坐标变换可以看做是经过无中间过程的一次性等效旋转形成,可表示为旋转矢量的形式:

式中:ua为在任意坐标系a系下的旋转瞬轴;φ为旋转角度。旋转矢量Φ对应的姿态变化四元数为
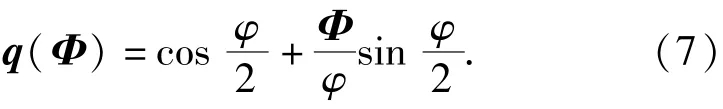
2 基于旋转矢量法的姿态解算
2.1数学框架
旋转矢量Φ的运动学方程,即Bortz方程[13-15]为

旋转矢量虽然不具有全局非奇异性,却满足局域非奇异性。基于此,可以采用旋转矢量的小量形式进行姿态解算,即把Φ看成是弹体坐标系从tk时刻到tk+1时刻角位置变化所对应的等效旋转矢量,而不是看成g系到b系的等效旋转矢量。这样,把每次数值解算之后以旋转矢量形式表示的姿态变化转移到姿态四元数当中,从而使得旋转矢量始终保持为小量。具体解算流程如下:
初值:已知初始姿态角(ψ0,ϑ0,γ0),则初始姿态四元数可表示为
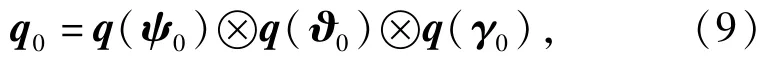
式中:ψ0=(0,ψ0,0);ϑ0=(0,0,ϑ0);γ0=(γ0,0,0).旋转矢量的初值为Φ0=(0,0,0).
龙格-库塔法解算:对于φ≠0,直接根据(7)式和(8)式计算姿态变化四元数和旋转矢量。对于φ=0,无法直接代入(7)式和(8)式进行计算。这时,根据旋转矢量的定义,(7)式取为
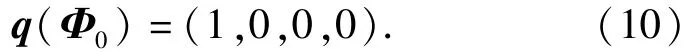
(8)式求极限可得

龙格-库塔法每次解算之后得到新的旋转矢量Φ,然后按(12)式计算姿态四元数:
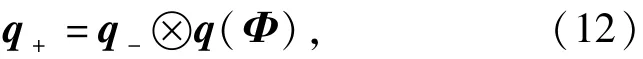
式中:q+为更新后的姿态四元数;q-为更新前的姿态四元数。由更新后的姿态四元数按(4)式可计算姿态角。当一个完整积分步长的计算完毕并且姿态四元数更新之后,置Φ=Φ0.
Bortz方程和其他关于位置、速度等变量的运动学和动力学方程构成了一组描述飞行器运动的、完备的常微分方程组[1-2]。整个运动方程中基于旋转矢量法的姿态计算流程如图1所示。

图1 基于旋转矢量法的姿态计算流程图Fig.1 Flow chart of attitude solution based on rotating vector
2.2旋转矢量法和四元数法
姿态四元数的运动学方程为

该方程的解[6]为
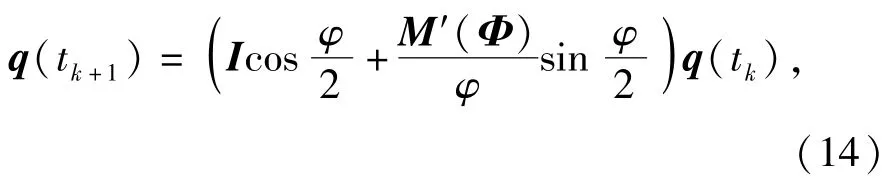
式中:

在采用龙格-库塔法进行数值解算时,旋转矢量Φ相当于采用(16)式近似计算:

式中:Δθ为由角速度直接积分得到的角增量。这相当于Bortz方程只保留了第一项。此时,(14)式即为四元数的毕卡算法。
置Φ=Δθ,对(14)式以Δθ为变量进行级数展开,可得四元数的有限阶近似算法。如对于4阶近似算法,有

已知4阶龙格-库塔法的截断误差为O(h5),h为计算步长[27]。由于每一步长h对应的角增量为Δθ,因此4阶龙格-库塔法的截断误差相当于O(Δθ5),即4阶龙格-库塔法等价于(17)式。类似分析可得,各阶龙格-库塔法等价于四元数毕卡算法相应阶次的近似算法。
由于四元数的毕卡算法只相当于旋转矢量的单子样算法[7],对有限转动引起的不可交换误差的补偿程度不够,所以不适合高动态飞行器运动姿态的解算。
另外,在对(13)式采用龙格-库塔法进行数值解算时,四元数会丧失其归一化特性,在每次数值更新之后需重新进行归一化。因此,基于四元数的姿态解算存在着归一化误差。由于旋转矢量是姿态的无约束表示,在由(7)式和(12)式计算姿态四元数时,整个过程归一化自动满足,只存在计算机的舍入误差。
2.3旋转矢量法和欧拉角法

由(18)式可见,如果ωx≫ωy,ωz≈0,即滚转通道是高动态的,另外两个通道是低动态的,那么由数值计算得到的Φy和Φz的不可交换误差将大于Φx的不可交换误差。但考虑到姿态角还需要按照(12)式进行计算,因此,基于旋转矢量算法的数值解算产生的不可交换误差对3个姿态角均有相当程度的影响。
另一方面,欧拉角的运动学方程为
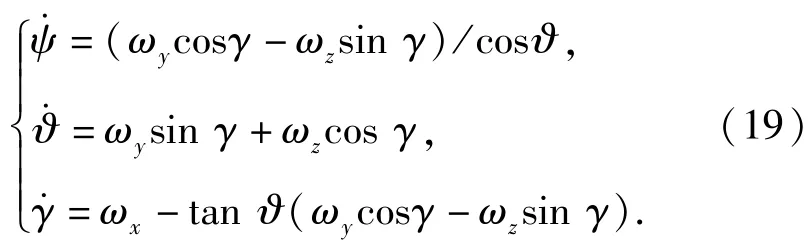
由(19)式可看出,3个欧拉角和角速度各分量之间相互耦合。对于面对称型飞行器来说,欧拉角法和旋转矢量法精度相当。对于轴对称飞行器(如滚转导弹)来说,一般采用准弹体坐标系来描述飞行器的运动,此时,(19)式变为

式中:ωqx、ωqy、ωqz为弹体坐标系b相对于地面坐标系g的角速度在准弹体坐标系q下的投影,它直接由描述转动动力学方程产生,不经过中间过程[1]。由(20)式可看出,对于滚转通道具有高动态的轴对称飞行器来说,滚转角的解算对另外两个姿态角解算没有直接影响,它只以滚转角速度的形式参与到描述转动的动力学方程中[1]。偏航角ψ虽然受不可交换误差的影响,但由于偏航和俯仰通道都是低动态的,因此解算精度也比较高。俯仰通道不存在不可交换项。这样,就通过准弹体坐标系的建立,把低动态的俯仰/偏航通道和高动态的滚转通道相对隔离开来。因此,基于准弹体系的欧拉角法的解算精度要比直接利用基于弹体系的旋转矢量法解算精度高。
为适于对滚转导弹这类飞行器进行姿态解算,同样可以建立基于准弹体系的旋转矢量算法。准弹体坐标系相对于地面坐标系只需要两个欧拉角(ψ,ϑ)即可描述。设Φ表示准弹体坐标系的角位置变化,则Bortz方程变为


(21)式和(22)式构成了滚转通道具有高动态的轴对称飞行器的姿态解算方程。
3 仿真验证
基于某型滚转导弹的运动方程对本文所提算法进行仿真验证。基准弹道基于欧拉角法解算,步长为0.1 ms.不同的姿态角算法只要步长足够小,都可以作为基准弹道的解算方法。数值计算方法采用4阶龙格-库塔法。下面对不同步长不同姿态角算法下的数值计算和基准弹道进行比较分析。
3.1旋转矢量法和四元数法
旋转矢量法和四元数法分别采用(8)式和(13)式进行计算,计算步长均为5 ms,时长为60 s.仿真结果如图2~图4所示。
由图2~图4可见,相比于旋转矢量法,采用四元数法计算时,不可交换误差和归一化误差影响十分明显。由于滚转通道动态比较大,因此,滚转角解算误差也较大。
3.2旋转矢量法和准弹体系下的欧拉角法
旋转矢量法和欧拉角法分别采用(8)式和(20)式进行计算。为对比明显,计算步长取为10 ms,时长为60 s.仿真结果如图5~图7所示。
由图5~图7可见,同样步长下,基于弹体系的旋转矢量法比基于准弹体系的欧拉角法解算精度要低。同时,由于步长的增大,旋转矢量法由于各通道耦合比较严重,低动态的俯仰和偏航通道由于受到滚转通道的影响,出现了明显的振荡现象,并有发散的趋势。
3.3准弹体系下的旋转矢量法和欧拉角法
旋转矢量法采用(21)式和(22)式,欧拉角法采用(20)式,计算步长取20 ms,时长60 s.仿真结果如图8~图10所示。
由图8~图10可看出,基于准弹体系的旋转矢量算法和欧拉角法解算精度几乎完全一样。这说明了旋转矢量算法应用的广泛性。

图2 偏航角误差曲线Fig.2 Curves of yaw angle error

图3 俯仰角误差曲线Fig.3 Curves of pitch angle error
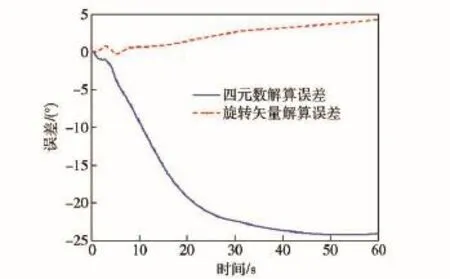
图4 滚转角误差曲线Fig.4 Curves of roll angle error

图5 偏航角误差曲线Fig.5 Curves of yaw angle error

图6 俯仰角误差曲线Fig.6 Curves of pitch angle error
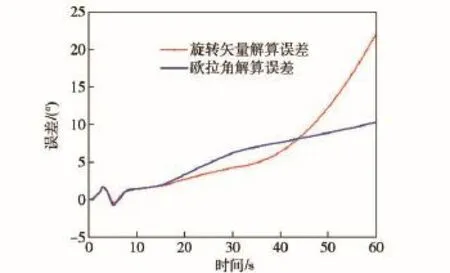
图7 滚转角误差曲线Fig.7 Curves of roll angle error

图8 偏航角误差曲线Fig.8 Curves of yaw angle error

图9 俯仰角误差曲线Fig.9 Curves of pitch angle error
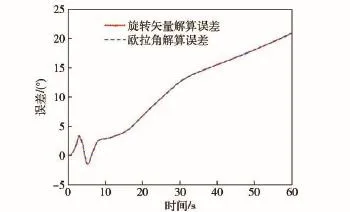
图10 滚转角误差曲线Fig.10 Curves of roll angle error
4 结论
1)基于旋转矢量是表示角位置变化所对应的等效旋转而不是角位置本身这一基本思想,同时借鉴旋转矢量在捷联惯性导航中的应用,本文建立了将旋转矢量应用于高动态全姿态飞行器运动方程的数学框架。既克服了欧拉角法不适于全姿态解算的缺点,同时,相比于四元数法又提高了高动态角运动情况下进行姿态解算的效率。
2)分析了不可交换误差和归一化误差对四元数法的影响,表明了旋转矢量算法的优越性。
3)比较分析了不可交换误差对旋转矢量法和欧拉角法在姿态解算中的影响。指出了在某些特定情况下欧拉角法解算精度优于旋转矢量法的原因,并据此建立了在单通道高动态情况下应用旋转矢量法的数学框架,从而使得旋转矢量法在这种情况下取得了和欧拉角法相当的解算精度。
4)数值仿真结果表明,本文提出的旋转矢量法不仅特别适用于高动态全姿态飞行器运动方程的解算,而且具有应用的广泛性。
(References)
[1] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008. QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Flight mechanics of missiles[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)
[2] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2012. FANG Zhen-ping,CHEN Wan-chun,ZHANG Shu-guang.Flight dynamics of aero vehicles[M].Beijing:Beihang University Press,2012.(in Chinese)
[3] Diebel J.Reprsenting attitude:Euler angles,unit quaternions,and rotationvectors[D].Standford:Standford University,2006.
[4] Greenwood D T.Principles of dynamics[M].Upper Saddle River,New Jersey:Prentice Hall,1988.
[5] 武元新.对偶四元数导航算法与非线性高斯滤波研究[D].长沙:国防科学技术大学,2005. WU Yuan-xin.Research on dual quaternion navigation algorithm andnonlinear Gaussian filtering[D].Changsha:National University of Defense Technology,2005.(in Chinese)
[6] 高钟毓.惯性导航系统技术[M].北京:清华大学出版社,2012. GAO Zhong-yu.Inertial navigation system technology[M].Beijing:Tsinghua University Press,2012.(in Chinese)
[7] 秦永元.惯性导航[M].北京:科学出版社,2010. QIN Yong-yuan.Inertial navigation[M].Beijing:Science Press,2010.(in Chinese)
[8] Deutschmann J,Markley F L,Bar-Itzhack I Y.Quaternion normalization in spacecraft attitude determination[C]∥Proceedings of the AIAA Guidance,Navigation,and Control Conference.Washington DC,US:AIAA,1991:908-916.
[9] Bar-Itzhack I Y,Deutschmann J,Markley F L.Quaternion normalization in spacecraft attitude determination[C]∥Flight Mechanics and Estimation Theory Symposium.Hilton Head Island:AIAA,1992:441-454.
[10] Schaub H,Junkins J L.Stereographic orientation parameters for attitude dynamics:a generalization of the Rodrigues parameters [J].Journal of the Astronautical Sciences,1996,44(1):1-19.
[11] Idan M.Estimation of Rodrigues parameters from vector observations[J].IEEE Transactions on Aerospace and Electronic Systems,1996,32(2):578-586.
[12] Crassidis J L,Markley F L.Attitude estimation using modified Rodrigues parameters[C]∥Proceedings of Flight Mechanics/Estimation Theory Symposium.Greenblt,MD:NASA-Goddard Space Flight Center,1996:71-83.
[13] Bortz J E.A new mathematical formulation for strapdown inertial navigation[J].IEEE Transactions on Aerospace and Electronic Systems,1971,AES-7(1):61-66.
[14] Savage P G.Strapdown inertial navigation integration algorithm design part 1:attitude algorithms[J].Journal of Guidance,Control,and Dynamics,1998,21(1):19-28.
[15] Shuster M.The kinematic equation for the rotation vector[J]. IEEE Transactions on Aerospace and Electronic Systems,1993,29(1):263-267.
[16] 杨绍卿.火箭外弹道偏差与修正理论[M].北京:国防工业出版社,2011. YANG Shao-qing.The trajectory error and correction theory of rockets[M].Beijing:National Defense Industry Press,2011. (in Chinese)
[17] Jordan J W.An accurate strapdown direction cosine algorithm [M].Washington DC,US:National Aeronautics and Space Administration,1969.
[18] Bortz J E.A new concept in strapdown inertial navigation[M]. Washington DC,US:National Aeronautics and Space Administration,1970.
[19] Miller R B.A new strapdown attitude algorithm[J].Journal of Guidance,Control,and Dynamics,1983,6(4):287-291.
[20] Lee J G,Mark J G,Tazartes D A,et al.Extension of strapdown attitude algorithm for high-frequency base motion[J].Journal of Guidance,Control,and Dynamics,1990,13(4):738-743.
[21] Jiang Y F,Lin Y P.Improved strapdown coning algorithms[J]. IEEE Transactions on Aerospace and Electronic Systems,1992,28(2):484-490.
[22] Musoff H,Murphy J H.Study of strapdown navigation attitude algorithms[J].Journal of Guidance,Control,and Dynamics,1995,18(2):287-290.
[23] Savage P G.Strapdown inertial navigation integration algorithm design part 2:velocity and position algorithms[J].Journal of Guidance,Control,and Dynamics,1998,21(2):208-221.
[24] Wang Z,Yin X,Li P,et al.Application of rotation vector algorithm for SINS attitude updating[C]∥Proceedings of the 12th IEEE International Conference on Signal Processing.Hangzhou,China:IEEE,2014:2390-2393.
[25] Wang Z,Chen X,Zeng Q.Comparison of strapdown inertial navigation algorithm based on rotation vector and dual quaternion [J].Chinese Journal of Aeronautics,2013,26(2):442-448.
[26] Stuelpnagel J.On the parametrization of the three-dimensional rotation group[J].SIAM Review,1964,6(4):422-430.
[27] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008. LI Qing-yang,WANG Neng-chao,YI Da-yi.Numerical analysis [M].Beijing:Tsinghua University Press,2008.(in Chinese)
Application of Rotating Vector in Equations of Motion for All-attitude Aircrafts
WANG Hong-hui1,2,YANG Shao-qing1,WU Cheng-fu2,HAO Feng1,CHE Xiao-tao1
(1.Xi’an Modern Control Technology Research Institute,Xi’an 710065,Shaanxi,China;2.School of Automation,Northwestern Polytechnical University,Xi’an 710072,Shaanxi,China)
A mathematical framework to apply a rotation vector in the equations of motion for all-attitude aircrafts is established based on the basic idea of that the rotation vector is to express an equivalent rotation corresponding to the change in angular position rather than the angular position.This idea is stimulated by the rotating vector in the strapdown attitude algorithm.The rotation vector method is available for all-attitude solution while the Euler angle method is not.Meanwhile,compared with the quaternion method,the rotation vector method can improve the efficiency of attitude solution.The non-commutative errors in the rotation vector method,the quaternion method and the Euler angle method are analyzed in detail. A rotation vector method based on the quasi-body frame is developed to improve the efficiency of attitude solution for axial-symmetry aircrafts of which a single channel has high dynamic characteristics.The digital simulations based on the equations of motion for some rolling missile show the effectiveness and generality of the rotation vector method.
control and navigation technoogy of aerocraft;rotation vector;Euler angle;quaternion;high-dynamic;all-attitude
TJ765.1
A
1000-1093(2016)03-0439-08
10.3969/j.issn.1000-1093.2016.03.008
2015-07-02
总装备部预先研究项目(1020702);陕西省博士后科研项目(2015年)
王红辉(1985—),男,博士后。E-mail:wanggh06@outlook.com;杨绍卿(1941—),男,中国工程院院士。E-mail:bq203rjc@163.com

