基于观测器与前馈控制技术的动态转台控制实验研究
张鹏,朱志刚,孙文利,胡吉昌
(北京航天控制仪器研究所,北京100039)
基于观测器与前馈控制技术的动态转台控制实验研究
张鹏,朱志刚,孙文利,胡吉昌
(北京航天控制仪器研究所,北京100039)
基于前馈控制技术对动态转台进行控制研究,分析了PID控制在动态转台控制中对于响应带宽提高的缺点。通过实验与Matlab结合辨识了开环系统模型,并与实际数据进行了比对。建立了系统状态观测器,并设计了基于观测器与前馈控制结合的控制器,证明了观测器与控制器的稳定性。最后通过实验证明了观测器与控制器的有效性。
状态观测器;模型辨识;带宽;双十;动态转台
0 引言
动态转台最初用于挠性陀螺的二倍频试验,速率陀螺固有频率、阻尼比、漂移测试和角加速度陀螺频率特性测试等[1],其性能指标直接关系被检测产品的检测精度。近年来,光纤陀螺及激光陀螺等高精度和小型化陀螺广泛应用于航天、航空领域的飞行器以及导弹等武器的导航与制导。航空、航天领域对飞行器及武器装备的机动性要求越来越高,对陀螺的频响带宽有了更高的要求。目前,光纤陀螺及激光陀螺的带宽基本达到100Hz以上,对性能指标要求高于惯性器件的角振动转台自然也面临着朝高频、大加速度方向发展[2]。同时,由动态转台发展成的仿真转台,是飞行控制系统进行地面仿真的关键设备[3],能模拟飞机飞行姿态和飞行动态特性,从而达到检验惯性导航与制导系统性能的目的,为实际试飞和进一步改进系统性能提供必要的、科学的参考数据。
对于动态测试转台一般以-3dB指标衡量系统的带宽,对于仿真转台为了系统能够真实地模拟实际情况常以“双十”指标(幅值误差小于10%,相位误差小于10°)衡量,可以看出仿真转台的指标要求比动态测试转台要严格很多。Yao Zhichao等提出了一种针对转台混合自适应控制算法,证明了系统的稳定性,并进行了仿真[4]。目前为止,对于仿真转台的控制基本采用一些经典的控制方法。梅等建立了三轴仿真转台的模型,并通过仿真证明了模型的有效性[5]。Long Manlin等提出了一种主动防扰动控制器,能克服干扰和非线性因素的影响[6]。Havlicsek等通过在台体上安装应力角加速度传感器,对角振动台进行控制[7]。以上的控制方法或者太复杂不容易在实际工程中实现,或者需要安装额外的传感器,也会增加系统的成本与结构复杂性。
基于观测器的控制方法避免了额外传感器的复杂性,同时实施起来比较简单。Liu Huixian等采用了预测控制方法研究了PMSM的速度调节问题,为了克服干扰的影响提出了预测控制加扩展观测器的方法[8]。Lee等基于状态扰动观测器研究了硬盘读写的鲁棒跟踪控制问题[9]。Gan等基于滑模滤波观测器研究了伺服转台低速时的摩擦补偿问题[10]。Yang等基于观测器研究了伺服电机驱动模型的在线辨识问题[11]。Wu Zhong等研究了伺服电机控制的位置与速度观测器[12]。以上的控制方法基本上限制于理论与实验室阶段,在工程中应用较少。
本文分析了在动态伺服系统PID调节中的弱点,采用实验辨识方法建立了开环系统传递函数模型。基于LabView软件建立了数字观测器,观测系统的速度状态,并通过引入速度反馈进入系统控制器,形成速度位置双闭环对系统进行控制。为了减小以误差项为主的控制器的天然劣势,在双闭环控制器的基础上,引入了前馈补偿控制技术,与双闭环控制相比增大了系统的响应带宽。为了验证对干扰的抑制能力,对低频小幅值正弦指令进行了实验。通过设计过程与实验结果可以证明本文的方法简单有效,并可用于实际工程。
1 开环传递函数模型辨识技术
机理建模法一般仅适用于简单系统的建模。对于复杂系统,要给出符合实际情况的合理假设有时是非常困难的。国外研究表明,当前系统辨识建模从精度、适用性、成本等各个方面都具备更好的发展和应用前景,可以成为机理建模的良好补充甚至是替代方法。由于整个系统的响应带宽比较宽,因此采用频率方法辨识系统模型。以某型单轴高频角振动转台为例,说明模型辨识的过程及准确性。在系统采样周期为125μs条件下,分别辨识不同转动惯量下的开环系统模型。
(1)负载转动惯量0.02kg·m2
采用Matlab频率辨识方法可得如下的离散模型:

转换为连续传递函数:

通过Matlab数值计算,可以得出实际曲线与辨识模型的近似度为99.23%,最终模型误差为0.1353,均方差为0.1258。
(2)负载转动惯量0.124kg·m2
采用Matlab频率辨识方法可得如下的离散模型:
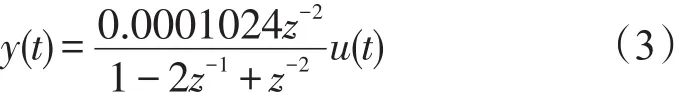
转换为连续传递函数:

通过Matlab数值计算,可以得出实际曲线与辨识模型的近似度为99.32%,最终模型误差为0.002017,均方差为0.001932。
(3)负载转动惯量0.19kg·m2
采用Matlab频率辨识方法可得如下的离散模型:

转换为连续传递函数:
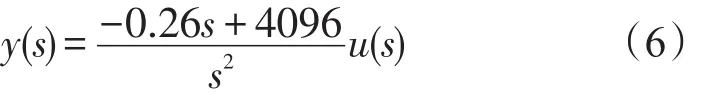
通过Matlab数值计算,可以得出实际曲线与辨识模型的近似度为98.77%,最终模型误差为0.002891,均方差为0.002728。
从以上的例子可以看出,在不同的负载情况下系统模型的结构是固定的,横型参数随着负载的不同而发生改变,同时也可以看出参数的变化关系基本和负载的变化一致。在本文的控制结构中采用扭矩控制,因此控制输入变量u可以看作电流、力矩或者加速度,它们三者之间存在比例关系,由此从式(2)、式(4)和式(6)可以比较直观地分析出系统响应与输入关系,输入的一次积分可以表示为与速度有关的变量,两次积分为位置相关的变量,因此系统输出为位置变量减去与速度相关的阻尼。
整个动态转台系统通用开环离散模型描述如下:

其中,M1、M2为传递函系数,当系统阻尼可以忽略时,M1=1,M2=2。
2 PID控制分析
2.1问题分析
到目前为止,PID控制算法仍然是工程上应用最广泛的方法。然而由于微分/差分项的存在,PID控制算法在动态转台的控制上有自身的弱点。假设传递校正函数表达式如下:

PID控制时系统的闭环传递函数为:
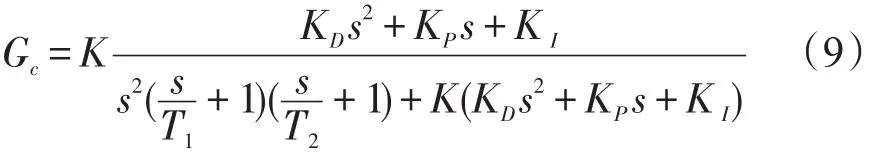
经推导可以得到动态转台系统响应幅值与相位与PID的参数存在如下的近似关系。
幅值特性为:

相位特性为:

其中,K'为与系统有关的常值。在结构带宽限制范围内,理论上只要增大PID参数就可以得到响应带宽很高的伺服系统,然而随着频率的增大,需要的KD越来越大,在实际系统中,当KD增大到一定程度会引起系统剧烈抖动,这种情况与系统存在扰动使系统反馈信号不平滑有很大关系。
2.2示例
为了验证存在谐波信号的正弦信号经过微分/差分后谐波信号幅值变大,通过对比带白噪声的正弦信号与差分/微分后的信号证明了分析的合理性。
图1中的信号在动态转台中可以看作为编码器采集信号与指令信号的误差,从图1可以看出,由于干扰的存在测量信号必然存在数字跳动,因此误差信号也会存在波动,虽然波动占误差信号比重不大,然而从差分后的图2(对应数字PID控制差分项)可以看出信号波动很大。差分/微分作用对小信号响应特别明显,主要体现在低频低幅与高频低幅区域。为了进一步提高系统的响应带宽,解决途径主要有两方面:抑制干扰;消除差分项。由于各种外界因素的存在,扰动信号不可能被完全消除,因此有必要设计一种不带差分项的控制方法,现代控制理论的状态空间与状态反馈是一种合适的选择。

图1 转台位置误差Fig.1Position error of turntable

图2 转台位置误差差分/微分Fig.2Difference of turntable's position error
3 状态观测器及控制器设计
为了利用状态进行反馈,必须用传感器来测量状态变量,但是并不是所有的状态变量在物理上都可测量,在转台控制系统中所需测量的状态主要为位置与速度,位置可由高精度编码器测量,然而速度传感器的安装实现存在着很多问题,比如增加结构复杂性、增加成本,同时也存在多传感器的信息融合问题等,于是提出了用状态观测器给出状态估值的问题,当模拟系统的估值与转台一致时,就可以用模拟系统的状态变量部分或者全部替代实际状态,进行状态反馈控制。
3.1状态观测器设计
在现代控制理论中,输入和输出构成系统的外部变量,而状态为系统的内部变量,这就存在着系统内的所有状态是否受输入影响和是否可由输出反映问题,也就是可控性和可观性问题。动态转台的离散状态方程表示如下:
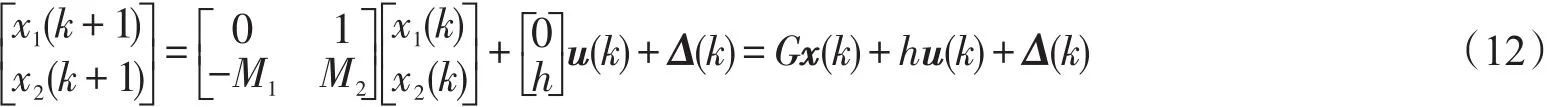
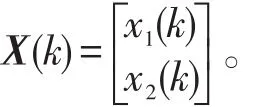

把式(13)代入式(12)可得:

则式(14)可以转化为如下状态方程:

在式(14)中,状态v1为位置变量,状态v2速度变量。
当系统模型精确时,可按极点配置的方法设计观测器参数,所谓的极点配置就是利用状态反馈和输出反馈使闭环系统的极点位于所希望的极点位置。由于系统的性能和它的极点位置密切相关,因此极点配置问题在系统设计中是很重要的。
被控对象的状态方程为:
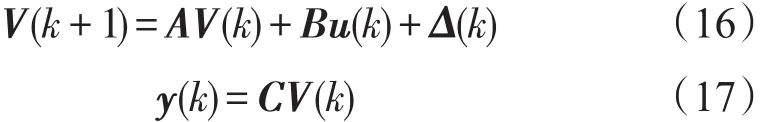
创建的模拟被控系统为:
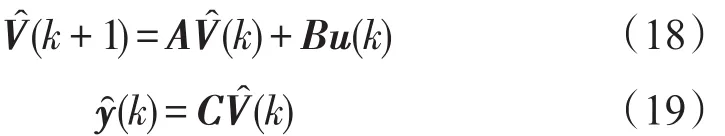
当模拟系统与被控对象的初始状态向量相同时,在同一输入作用下,有V̂(k)=V(k),可用V̂(k)作为状态反馈所需用的信息。然而在大多数情况下,两个系统的初始状态总有差异,既是两个系统的A、B、C矩阵完全一样,也必定存在误差V̂(k)-V(k)=e(k),从而导致误差ŷ(k)-y(k)存在,而被控系统的输出量是可以用传感器测量的,于是根据一般反馈原理设计观测器参数使V̂(k)-V(k)尽快逼近于零。
根据全维观测器及观测器原理图,观测器的动态方程为:
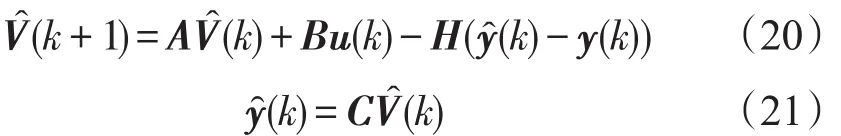
根据式(11)~式(20)可得:

由前面的可观性推导可得矩阵(A-HC)的极点可以任意配置。要想使系统误差尽快趋近于零,要求离散系统的极点位于单位圆内,然而离散系统的动态特性与闭环极点在单位圆内的分布密切相关。以下通过简单的方法证明极点关系与误差情况。
构造李雅普诺夫函数如下:
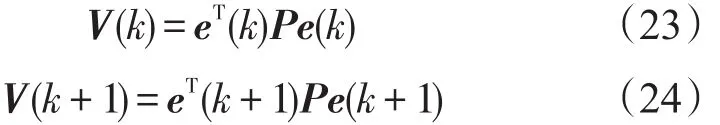
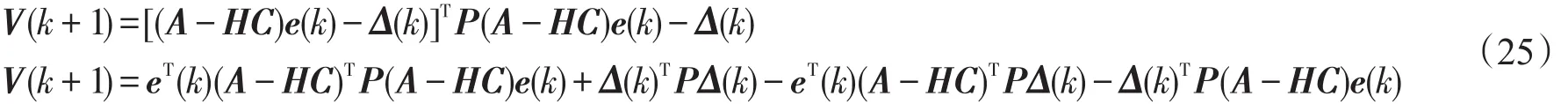
因此,
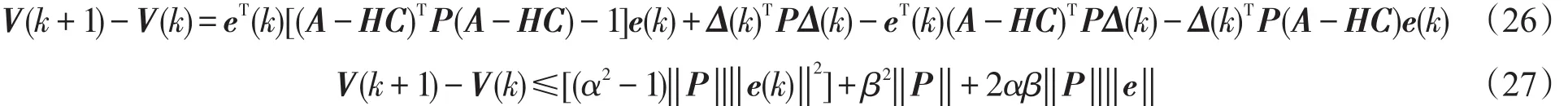
为了保证系统渐进稳定,
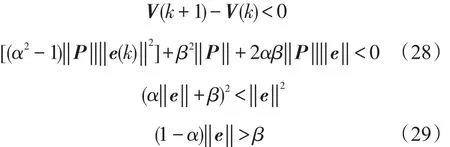
因此,α越小即特征值越接近原点,误差越小,α特征值由观测器矩阵H决定。
3.2状态反馈控制器设计
前面的观测器设计很好地解决了状态的估值问题,当模拟系统能够准确地跟踪实际系统时,模拟系统的状态变量可以用作实际系统的状态反馈,因此我们可以从模拟系统中提取速度分量,形成速度闭环,因此整个控制系统分成了电流环、速度环、位置环。
设计适当的位置与速度控制器,可以得到响应带宽很高的动态转台。为了便于分析系统误差与响应关系,在连续状态下分析了控制器的设计。控制中比例控制器,比例系数分别为kp和kv。假设此时的模拟系统能够精确跟踪转台实际系统,因此速度ẋ可以用模拟的速度x̂̇辨识得到。
(1)加速度前馈
设计的加速度前馈控制器连续状态下可表示为:

把控制器带入到系统状态方程可以得到:
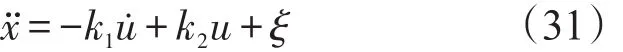
令e=x-xd,把式(30)代入式(31)可得系统闭环方程:

从式(31)可以得出,只要设计适当的参数kp和kv,保证1-k1kv>0,k2kv-k1kp>0,可以使误差趋近一个有界范围。同时,可以通过解式(32),计算系统的收敛时间。从式(32)可以得到系统的稳态误差为:
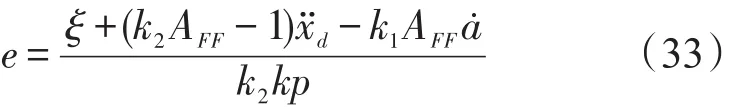
带有速度反馈的双闭环控制系统的控制效果要比单闭环的位置环控制效果好很多,能够达到比较宽的响应带宽,并且系统的控制结构比较简单。
(2)速度加速度前馈
基于速度加速度的前馈控制器连续状态下可表示为:

把式(34)代入式(31)可得系统闭环方程:
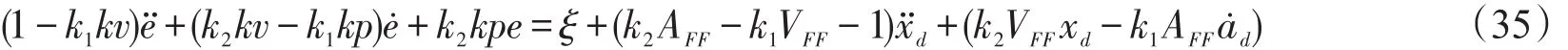
同样,从式(35)可以得出,只要设计适当的参数kp、kv、AFF、VFF,保证1-k1kv>0,k2kv-k1kp>0,可以使误差趋近一个有界范围。
kp为位置反馈增益,kv为速度反馈增益,VFF为速度前馈增益,AFF为加速度前馈增益。xd、vd、ad分别为指令位置、速度及加速度。

式(34)可以转化为如下结构:

设计适当的参数可以得到如下等式:
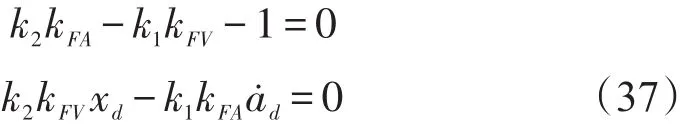
设李雅普诺夫函数如下:

Q是正定矩阵,
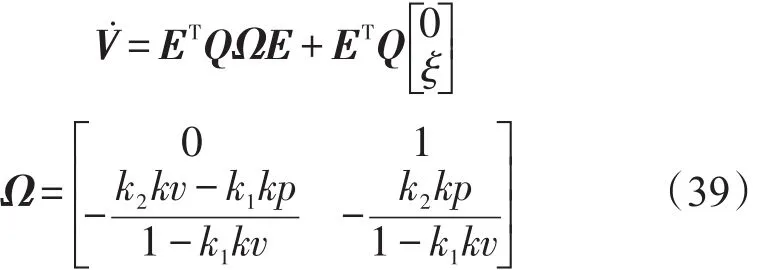
φ=maxλ(Ω),φ是Ω的最大特征值,因此:

为了保持稳定性,有:
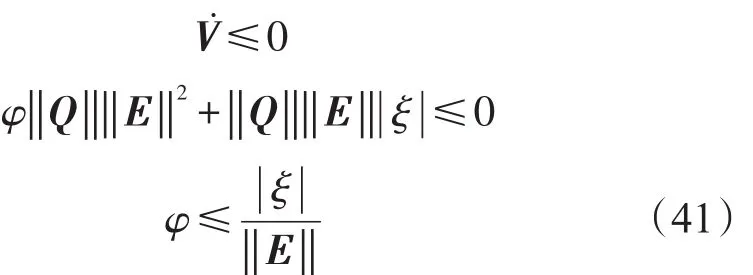
上述推导证明了系统稳定性条件及误差范围。
4 实验结果
4.1控制效果
为了验证观测器与控制器的控制效果,分别对带不同负载的情况进行研究。文中所用编码器线数为18000,因此整圈脉冲数为18000×4×32=2304000,1°对应的脉冲为6400,具体体现在实验结果图中。

图3 J=0.124kg·m2响应Fig.3Response of J=0.124kg·m2
当转动惯量J=0.124kg·m2时,如图3所示。设计的观测器参数H1=1.8,H2=1.81,此时的两个离散极点为0.1,为了保证系统快速跟踪输入的正弦函数,动态控制参数为kp=12,kv=0.15,kI=1,Ilim=500,VFF=-0.01,AFF=0.00012。
从实验结果曲线可以发现,观测器输出与编码器采集信号之间存在一个采样周期,即125μs误差,能够比较准确地跟踪实验值。
当系统转动惯量变为J=0.19kg·m2,为了使系统仍达到原来的带宽,此时控制参数为kp=25,kv=0.28,kI=1,Ilim=1000,VFF=-0.013,AFF=0.00018。观测器参数不变,系统的跟踪效果如图4所示。
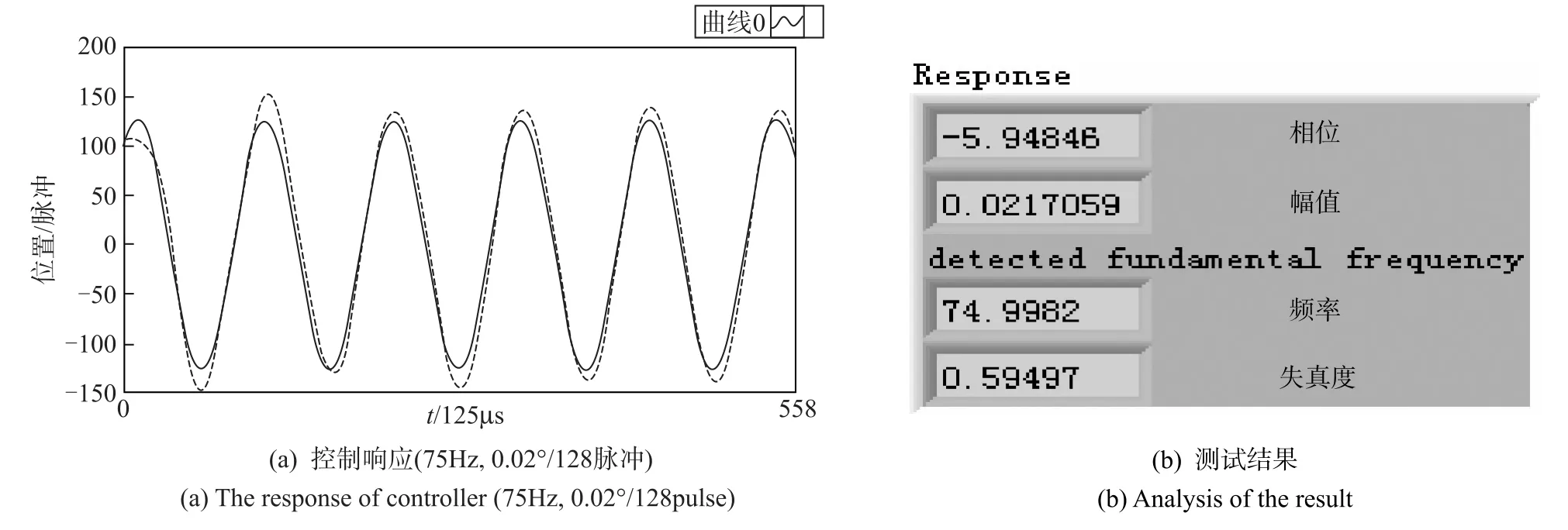
图4 J=0.19kg·m2定频响应Fig.4Response of J=0.19kg·m2
可以看出文中所设计的控制器在转台响应带宽的控制中有很好的效果,在转台负载变化的条件下仍可以得到较高的响应带宽。
4.2低频小信号指令响应分析
对于动态转台除了要提高系统的响应带宽,对于低频小信号的跟踪能力也是一个严苛选项。为了验证动态转台具备低频、小信号精确跟踪能力,给出了某型动态转台的低频小信号角振动跟踪实测结果,如图5所示。其中控制方法采用基于观测器的控制,实时计算机的循环周期为1ms,数字化控制环节的采样周期为125μs。
从实际检测曲线可以看出,设计的观测器控制器系统在满足大动态加速度带宽条件下,同时也很好地兼顾了跟踪低频小信号的要求。
5 总结
本文对模拟转矩控制的动态转台的模型进行了实验研究,给出了模型的表达式,设计了状态观测器,用来观测状态反馈控制中的状态变量,
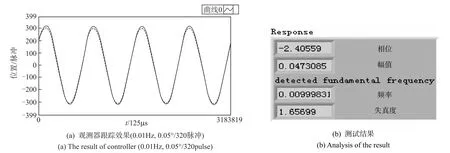
图5 低频小信号响应分析Fig.5The result of low frequency and small amplitude
基于状态变量设计了位置/速度双闭环控制器,并通过前馈控制技术补偿了相位与幅值误差。最后通过对转台响应带宽进行实验,验证了观测器与控制器的有效性。与PID控制相比双闭环控制对转台响应带宽的提高比较大,然后这种控制方法仍然是以误差控制为主,控制量中存在干扰信号,需要在接下来的研究中解决。
[1]陈振,刘向东,等.一种改进的重复控制器在高频角振动转台中的应用[J].电工技术学报,2008,23(11):178-182. CHEN Zhen,LIU Xiang-dong et al.A modified repetitive controller and its application to high-frequency angular-vibration table[J].Transactions of China Electrotechnical Society,2008,23(11):178-182.
[2]王雪峰.飞行仿真转台品质整定与先进控制方法研究[D].南京航空航天大学,2004. WANG Xue-feng.Research on performance improvement and advanced control method of flight simulator[D].Nanjing University ofAeronautics andAstronauics,2004.
[3]马骥,李大琦,邹秀斌,等.高频角振动转台控制系统设计与仿真分析[J].航空精密制造技术,2012,48(2):21-24. MA Ji,LI Da-qi,ZOU Xiu-bin,et al.Computer simulation analysis and design of high frequency angular vibration turntable system[J].Aviation Precision Manufacturing Technology,2012,48(2):21-24.
[4]Zhichao Yao,Weihong Wang,Lianqiang Zheng,et al.A hybrid adaptive control for flight simulator turn table[C]. International Conference on Mechatronics and Automation,2010:773-777.
[5]Xiaorong Mei,Ming Chen,Guizhen Bai,et al.Modeling and simulation of three-axle flight simulation table[C]. Proceedings of the 6thWorld Congress on Intelligent Control andAutomation,2006:6165-6168.
[6]Manlin Long,Yongling Fu,Shuangqiao Chen,et al. Flight simulator table servo control based on ADRC strategy[C].Proceedings of the 29thChinese Control Conference,2010:3497-3501.
[7]Howard S.Havlicsek.Strain gage angular acceleration sensor facilitates precise control of vibration table[C]. Symposium Gyro Technology,Stuttgart,Germany,1999.
[8]Huixian Liu,Shihua Li.Speed control for PMSM servo system using predictive functional control and extended state observer[J].IEEE Transactions on Industrial Electronics,2012,59(2):1171-1183.
[9]Seung-Hi Lee,Hyun Jae Kang,Chung Choo Chung.Robust fast seek control of a servo track writer using a state space disturbance observer[J].IEEE Transactions on Control Systems Technology,2012,20(2):346-355.
[10]Minggang Gan,Huixia Ma.Repetitive adaptive control based on sliding filter observer in servo turntable[C]. Proceedings of the 10thWorld Congress on Intelligent Control andAutomation,2012:116-121.
[11]Shengming Yang,Jinde Lin.Observer-based automatic control loop tuning for servo motor drives[C].IEEE 10thInternational Conference on Power Electronics and Drive Systems(PEDS),2013:302-305.
[12]Zhong Wu,Yuntao Wu.Design of angular position and velocity observer for servo motors with reslovers[C]. Proceedings of the 31stChinese Control Conference,2012:4350-4355.
Model Identification and Control Study Based on State Observer of Dynamic Turntable
ZHANG Peng,ZHU Zhi-gang,SUN Wen-li,HU Ji-chang
(Beijing Institute ofAerospace Control Devices,Beijing 100039)
The control based on state observer of dynamic turntable is studied.The disadvantage of PID in increasing the bandwidth of dynamic turntable is analyzed.In order to design the state observer,the experiment of open-loop is carried out.The open-loop model is got by Matlab.The model and experimental data are compared.The state observer and the controller based on the observer are designed.The stability of observer and controller is proven.The effectiveness of the observer and controller is proven by the experiment in single axis turntable.
state observer;model identification;bandwidth;double ten;dynamic turntable
U666.1
A
1674-5558(2016)05-01037
10.3969/j.issn.1674-5558.2016.01.019
张鹏,男,博士,工程师,研究方向为伺服控制。
2014-12-09

