蚁群算法在多目标TSP问题中的应用研究

刘争艳，江洁莉，李　絮

（阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037）

蚁群算法在多目标TSP问题中的应用研究

刘争艳，江洁莉，李絮

（阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037）

鉴于蚁群算法在处理组合优化问题中的优势，本文针对多目标TSP问题，对蚁群算法进行深入研究，探索多目标环境下蚁群算法的运行机制，同时构建多目标蚁群算法框架，并设计优化算子。仿真实验结果验证了本文算法的可行性与有效性。

蚁群算法；Pareto最优；多目标优化；旅行商问题

蚁群算法是受自然界中蚂蚁觅食行为的启发，由意大利学者Marco Dorigo等人于1991年提出的一种启发式仿生优化算法。由于具有分布式控制，正反馈自催化机制以及潜在的并行性等特点，蚁群算法被越来越多的应用到各类优化问题中，并在求解诸如旅行商问题（Traveling Salesman Problem，TSP）之类的组合优化问题中效果显著［1-4］。前期我们对蚁群算法进行了一些研究，并应用到单目标TSP问题的求解中，取得了良好的效果［5］。然而，现实世界中的很多问题通常不止一个优化目标，往往是由相互冲突的多个目标组成，以具体的TSP问题为例，现实中需要考虑的常常不止路程最短这一个目标，还要同时考虑诸如时间最少、费用最省、风险最小等方面的目标［6］。因此，对多目标TSP问题进行研究更具有现实意义。

1　多目标TSP问题

TSP问题可叙述如下：某旅行商要经过n个城市并回到原出发城市，除起点外，每个城市都必须且只允许经过一次，要求寻找所有城市之间一条最短的路径。因此，通常的TSP问题只有一个目标，即路径最短，而多目标TSP问题的目标除了路径最短之外，还有诸如时间最少、费用最省、风险最小等方面的目标。

为了能够更好地描述该问题，选择两个目标建立数学模型，一个目标为路程最短，用目标函数f1表示，另一个目标为费用最省，用目标函数f2表示，那么多目标TSP问题数学模型定义如下［7］：

其中，D（i，i+1）表示城市i和城市i+1间的距离，C（i，i+1）表示城市i和城市i+1间的费用。

2　求解多目标TSP问题的蚁群算法

2.1算法流程

算法的基本流程描述如下：

步骤1针对优化问题的各个目标，分别进行参数初始化；

步骤2利用蚂蚁构建优化问题的可行解；步骤3根据各目标参数，对可行解进行局部信息素更新；

步骤4对可行解进行非支配解的计算，并更新非支配解外部存档；

步骤5对外部存档中所有非支配解进行全局信息素更新；

步骤6终止条件不满足，转步骤2；

其中，步骤4非支配解的计算方法采用NSGA-ⅠⅠ中非支配排序算法［8］。下面对算法中涉及的其他关键操作进行详细介绍。

2.2参数初始化

算法的参数初始化主要是对信息素值和启发式信息值进行初始设置。信息素值的初始化与ACS算法［9］的初始设置类似，即针对每个优化目标，首先使用最近邻方法计算得到该目标的初始最优值Len，然后再计算得到该目标信息素的初始值。如第k个优化目标的信息素初始值表示如下：

其中，n为蚂蚁个数。

启发式信息值的初始化一般取权重（如城市间的距离、费用等）的倒数，同时，为了使算法能够在各个目标间均衡搜索，对所有目标的启发式信息值进行标准化，将其统一到一个相同的标准下。如第k个优化目标中路径（i，j）上的启发式信息值表示如下：

2.3可行解的构建

在参数初始化之后，利用蚂蚁构建多目标优化问题的可行解。算法中选择下一个城市节点采用伪随机比例选择机制，如以两个优化目标为例，蚂蚁m由所在城市i选择下一城市j的方式如下：

其中，J按下式所示的概率选择下一节点：

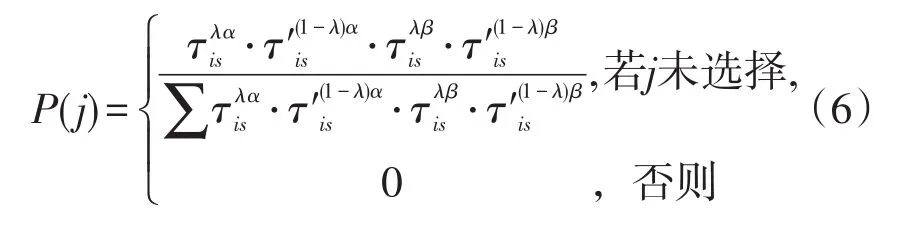
在式5和式6中，s为蚂蚁未经过的城市列表，和分别为两个目标在边（i，j）上的信息素值，和为对应的启发式信息值，α和β为启发式因子，λ为目标权值参数，q为［0，1］之间任一随机数，设置每只蚂蚁代表不同的目标权值，蚂蚁m的λ值通过下式给出：

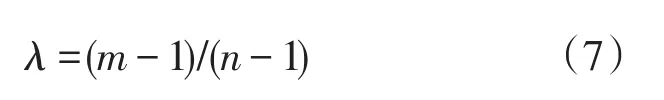
其中，n为蚂蚁个数。

2.4信息素更新方式

本文算法中采用局部信息素和全局信息素相结合的信息素更新方式。

在蚂蚁构建得到可行解之后，首先进行局部信息素更新，即针对不同目标对可行解路径进行信息素的挥发控制，具体更新方式如下：

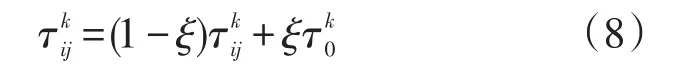
在局部信息素更新后，使用非支配排序算法对所有可行解进行计算，得到非支配解集，并更新非支配解外部存档，同时对外部存档中所有非支配解进行全局信息素更新。具体更新方式如下：

3　仿真实验

本文从TSP实例库TSPLⅠB（http：//elib.zib.de/ pub/mp-testdata/tsp/tsplib/）中选取两个具有100个城市节点的TSP问题：kroA100和kroC100，其城市节点间的距离分别作为路径长度权值和费用权值。实验参数设置如表1所示。

表1　实验参数

为了避免受随机性的影响，对算法进行5次独立实验，绘出算法求出的Pareto最优前沿面，同时为了观察目标权值参数λ对不同目标的影响，将路径长度目标和费用目标权值分别按照公式7进行设置，运行结果如图1和图2所示。同时，对5次实验找到的各目标上的最优值以及非支配解集的最大个数进行统计和分析，结果如表2所示。

图1　实验运行结果（路径目标权值取λ）

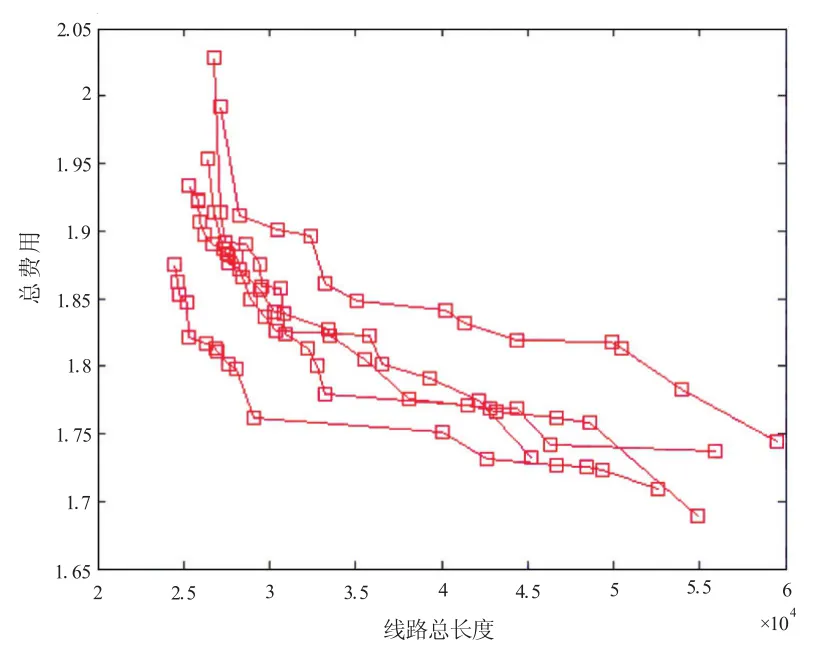
图2　实验运行结果（费用目标权值取λ）

从图1、图2和表2中可以发现本文算法得到的Pareto前沿分布较均匀，范围较广，也能够观察到目标权值对不同目标的影响。表2中算法找到的路径长度最优值约为24 495，接近TSPLⅠB中给出的kroA100问题的最优值21 282，费用最优值约为23 631，也接近kroC100问题的最优值20 749。因此，本文设计的算法是可行且有效的。

表2　实验结果数据分析

4　结束语

本文结合多目标优化问题及TSP问题的特点，对蚁群算法进行了深入研究，探索多目标环境下蚁群算法的运行方式，并构建了多目标蚁群算法框架。最后通过对典型的双目标TSP问题进行仿真实验，验证本文设计的算法是可行且有效的。下一步的工作主要是拟结合云模型理论，来继续完善算法自身机制，进一步提高算法性能。

［1］ 裴振兵，陈雪波.改进蚁群算法及其在机器人避障中的应用［J］.智能系统学报，2015，10（1）：90-96.

［2］ 费腾，张立毅，孙云山.基于DNA-蚁群算法的车辆路径优化问题求解［J］.计算机工程，2014，40（12）：205-208，213.

［3］ 李擎，张超，陈鹏，等.一种基于粒子群参数优化的改进蚁群算法［J］.控制与决策，2013，28（6）：873-878.

［4］ 刘全，陈浩，张永刚，等.一种动态挥发率和启发式修正的蚁群优化算法［J］.计算机研究与发展，2012，49（3）：620-627.

［5］ 李絮，刘争艳.基于云模型的模糊自适应蚁群算法研究［J］.计算机工程与应用，2016，52（2）：24-27.

［6］ 魏心泉，王坚.多目标资源优化分配问题的Memetic算法［J］.控制与决策，2014，29（5）：809-814.

［7］ 朱云飞，蔡自兴，袁琦钊，等.求解多目标旅行商问题的混合遗传算法［J］.计算机工程与应用，2011，47 （7）：52-56.

［8］ Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-ⅠⅠ［J］.ⅠEEE Transactions onEvolutionary Computation，2002，6 （2）：182-197.

Application of ant colony algorithm in multi-objective TSP problem

LⅠU Zheng-yan，JⅠANG Jie-li，LⅠXu

（School of Computer and Information Engineering，Fuyang Normal University，Fuyang Anhui 236037，China）

Because of the advantages of ant colony algorithm in combination optimization problems，this paper studies deeply ant colony algorithm for multi-objective TSP.The paper mainly explores operating mechanism of ant colony algorithm in multi-target environment，builds the framework of multi-objective ant colony algorithm，and designs optimization operator.Simulation results prove the feasibility and effectiveness of the proposed algorithm.

ant colony algorithm；Pareto optimal；multi-objective optimization；traveling salesman problem

TP242

A

1004-4329（2016）01-055-03

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）01-055-03

2015-10-20

安徽省教育厅自然科学基金项目（2014KJ021，2014KJ023）；安徽省质量工程项目（AH201410371029，2013zy167）；阜阳师范学院质量工程项目（2013ZYSD05，2014JXTD01）资助。

刘争艳（1981-），男，硕士，讲师，研究方向：视频图像处理、智能优化。