英国数学英才选拔考试MAT命题技术分析
廖运章,王华娇
英国数学英才选拔考试MAT命题技术分析
(1.广州大学数学与信息科学学院,广东广州 510006;2.广州大学附属东江中学,广东河源 517500)
数学入学考试MAT是英国重要的数学英才选拔考试,是牛津等大学数学、计算机及相关专业的入学条件之一,数学知识与方法相当于A水平核心数学C1和C2模块水平,但问题设计却不同,重在考查考生理解A水平数学的深度而非广度.MAT的命题特征是:控制运算量,解题思维多样;分层递进设计,考查数学探究能力;构建新情境,渗透数学建模思想,考核信息加工能力;因循专业所需,甄别不同数学能力.
数学英才;牛津大学;MAT;命题技术
近年来,英国学生在国内GCSE和GCE-A水平数学考试获或的人数屡创新高,如首次引入GCSE成绩等级的1994年只有10.5%学生获或,2013年这一数据则变为22.6%.但英国学生在PISA和TIMSS等国际学生能力评价中成绩却持续下降,不尽如人意,如英国15岁学生PISA数学成绩排名2009年第28位,2012年第26位,用人单位和高校也抱怨学生没有具备工作或进一步学习所必需的基本数学知识技能,中小学数学教育质量受到公众的普遍质疑,引起英国朝野关注,并由此提出基于国际证据的改革教育新主张[1].
为遴选数学英才,剑桥和牛津对报读其数学、计算机及相关专业的申请人设置数学附加入学考试,剑桥的第六学期考试STEP(Sixth Term Examination Papers)[2],牛津的数学入学考试MAT(Mathematics Admissions Test)正是英国两项久负盛名的数学英才选拔考试(其他大学如帝国理工学院等也鼓励申请者参加该两项考试).其中,MAT重在考查考生理解数学的深度而非广度,对中国数学考试命题(尤其是大学自主招生考试)具有借鉴意义.以下依MAT官网公布的2007—2014年试题,从内容领域、题型题量、命题方法等方面,分析MAT试题的命题技术及其启示作用[3].
1 MAT试题的内容分布
MAT主要依据其2007年发布的考试大纲命题,内容要求相当于A水平核心数学C1和C2模块水平[4~8],但问题设计却不同,考纲包括多项式、代数、微分、积分、图象、对数和乘方、变换、几何、三角函数、数列与级数等10部分内容.
MAT考试时长2.5小时,全卷满分100分,共7大题.2007—2013年第1题为单项选择题,含A~J共10小题,每小题4分,共40分,2014年起选项由4个变为5个;第2~7题为解答题,考生需根据申请专业选做其中的4题,每题15分,多做或做其他专业的题不得分;牛津大学的数学、数学与哲学、数学与统计学专业/课程做1、2、3、4、5大题,数学与计算机科学专业/课程做1、2、3、5、6题,计算机科学、计算机科学与哲学专业/课程做1、2、5、6、7题,帝国理工学院数学、计算机及相关专业做1、2、3、4、5题;考试不能使用计算器、公式表、词典[9].不难发现,题1、2、5共用,数学(含统计)和计算机科学兼有的共性题是3和6,区分两者之差异的题为4和7,分层设计试题的理念显而易见.
为合理统计选择题的学科领域分布,采用主知识点划分原则,即若题中涉及多个知识点以一个主要知识点所在领域为准,如2011年第1-F题:已知满足0≤<,且方程表示圆,则取值范围是,,,任意值.方程化为,由半径有,又0≤<≥0,故,选.本题涉及多项式中的完全平方式、代数中的解简单不等式、图象中的用图象解不等式、几何中的圆方程、三角函数中的恒等变形等知识点,但主体应为三角,所有归为三角函数领域.依此统计,第1题选择题中,微积分19道(微分8道、积分11道)、方程和不等式17道(多项式12道、代数5道)、函数及其图象19道(图象9道、对数和乘方9道、变换1道)、几何与三角18道(几何7道、三角11道)、数列9道,内容布列均匀,体现了各专业对数学的共同要求.
统计显示,解答题的内容领域是相对稳定的,一般地,第2题主要考查函数、方程、不等式与数列(2007、2012函数迭代,2008、2009递推数列,2010、2011方程与圆,2013函数方程,2014方程和不等式),第3题以微积分为主,第4题重在三角、几何,第5题是新信息迁移问题,第6题是逻辑推理问题,第7题是与计算机科学相关的问题.
2 MAT试题的命题特色
MAT试题的基本特点表现为题型题量保持相对稳定,背景单纯、知识点不多、难度维持在0.5左右(近5年1~5题的平均分为),这得益于其命题设计上的持续创新.
2.1 控制运算量解题思维多样
“减少运算量,增加思维量”一直是中国高考数学命题追求的理想愿景,多年命题亦不遗余力地付诸实践并取得一定成绩,但距离实现这一目标仍任重道远,如何予以改善?MAT的积极探索,可谓他山之石.宏观上,MAT把重思维轻运算理念作为贯穿整套试卷始终的设计原则,整体减少运算量,所有试题的解答无需繁杂计算,但要有数学的头脑、严密的思维,解题思维多样;微观上,从隐性与显性维度控制运算量,确保较好的区分度.
本题就是一道比较典型的隐性控制运算量问题,解题入口宽,方法多样,思辨地解答则方便快捷,用算法化计算耗时费力、容易出错.注意到对称变换(反射)的保持长度不变之性质(和长度相等),以及是单位向量,易知为正确答案;也可用极端化思想,即若越来越大则直线越逼近轴,最终只有能取到点(-1, 0).如若用常规方法,设点的坐标建立过两对称点且垂直于对称轴的直线方程解联立方程组求出垂线中点坐标再由中点公式求出的坐标(“垂直又平分”),过程冗长,即便利用的特殊值计算,出错率也不低(不凑效).
对于显性控制运算量,指的是在题中明示不用计算,而是要求说理,“无需计算,解释为什么……”、“解释你的答案”、“无需求拐点坐标”等是常见的用词,这种告白式减少运算量的做法,中国并不多见.
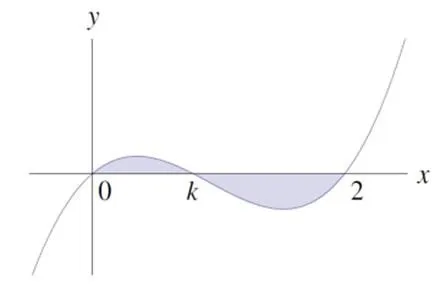
图1 函数的图象
如例2的问题,历届MAT试题数量不少,其目的是尽量减少无谓的运算,着眼于考量数学思维量.显然,,该积分可化为,其中、分别是2次和3次多项式,若设其积分依次为、,则,易知这是次数不超过4的多项式.因无需进行定积分运算求,避免了因出错而导致(ii)、(iv)、(v)的正确解答,各小问环环紧扣,层次分明,淋漓尽致地展现了少运算重思维的命题技术.当然,如果直接计算
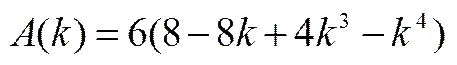
那么题目就直白平淡了.
中国近年全国及分省命制的高考数学试题,每年几乎都设有形如的含参函数问题,但试题设计与例2大相径庭,形式单一,大都涉及利用导数解决有关函数单调性、零点、最值、不动点、不等式以及由衍生的数列迭代等问题,运算量大(如反复多次构造函数求导),往往作为压轴大题出现,难度可想而知.
2.2 分层递进设计考查数学探究能力
遵循数学思维的内在步骤,从特殊到一般、由易及难、分层布列试题,以探究数学对象的规律和解决数学问题的规律,考查学生数学探究能力,是MAT命题的常态,MAT解答题几乎都如此设计,一题多问、一个关键思维节点设问、逐次递进等是常用的命题手段,即前几问较为简单,但渗透着解决这类问题的思路或方法,并将这一思路或方法迁移到后面复杂问题的解决.这样设计,既有利于学生在新情境中学习新方法,更重要的是考查申请者学习数学的潜力.
这是函数迭代问题,若只要求完成(iii)、(iv),需要重复使用和迭代,直接计算有难度,且不易发现两小题间的内在关系,使人望题怯步、无从下手.通过(i)、(ii)小题的铺垫和引导,就能逐次迭代得出结果,从而由推出(iv).如果直接要求解决(iv),解题难度更大.可见,本题倘若没有分层递进设计,运算量“繁死你”、思维量“想死你”(想不出解题思路)难免发生.
2.3 构建新情境并渗透数学建模思想以考核信息加工能力
构建问题情境(实际情境和数学抽象情境)是MAT命题的重要特色,与STEP等其他测试不同,MAT试题涉及的实际情境(个人生活、公共生活与科学情境)数量有限,一般分布在第5、6、7题,除科学情境外大多平实简单,渗透最基本的数学建模思想;而数学抽象情境属于新概念、新运算、新定理等“新信息迁移问题”,重在考查学生在新的信息和情境下,独立获取、加工和运用新信息的能力,以及继续学习数学的潜能和创新意识.面对数学新情境,无现成经验借鉴,现场读懂新概念、理解新原理、获取新信息,恰当表征所定义数学概念或符号的涵义是正确解题的前提或关键.
例4(2012年第5题) 一特定机器人可执行以下3个命令,即:向前移动1个单位距离;:向左转90°;:向右转90°.程序就是一系列命令,程序≥0)定义如下:表示机器人只执行向前命令;≥0)表示先执行、继而左转、再执行、最后右转,即,如.(i)写出;(ii)执行程序后,机器人走了多远?即它执行了几次命令;(iii)设为程序中执行的命令总数,如,,建立与的关系方程,并写出关于的表达式,不需证明(提示:考虑);(iv)机器人面朝轴正向、从原点出发,执行程序后,面朝哪个方向?(v)图2左是机器人执行程序的行走路径,在图2右中画出机器人执行程序的行走路径;(vi)设为机器人执行后的坐标,如,,求与的关系方程,并计算、的值.
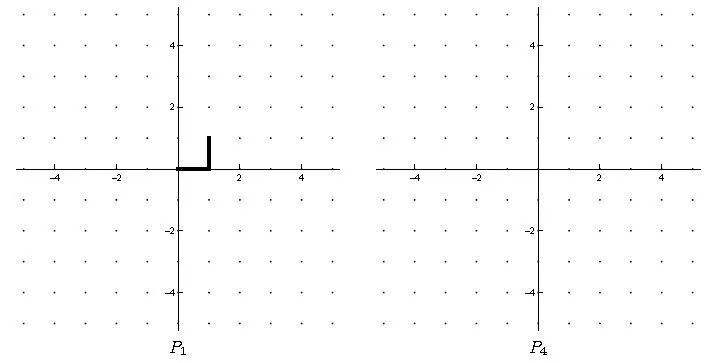
图2 机器人行走路径
这道背景简洁的数列新定义试题,蕴含着素朴本真的数学建模思想,准确把握程序的递归定义就不难解决,这也是衡量考生是否具备数学“可持续发展能力”的重要尺度.由递归定义易得:;若记为程序中执行命令的个数,则,而,故;同时,可求;因每个包含、的数量相同,机器人执行程序后仍面朝轴正向,路径图亦不难作出(此略);,注意到,,,于是,.
2.4 因循专业所需甄别不同数学能力
除要求学生具有良好的共有数学基础外,根据不同专业的数学需求,设置不同层次的数学试题以考查不同的数学能力是MAT命题的又一亮点.第4题主要针对数学专业(含统计),内容侧重函数、三角与几何的综合,试题年年附有图象,提倡数形结合;第7题是专为计算机科学专业设计的,一般不涉及高深的数学知识,往往与计算机科学中的编程等密切相关,如字符串排列、有限自动机理论等;第6题是数学与计算机领域兼有的逻辑推理问题,突出逻辑推理能力的考查,要求考生具备缜密的逻辑思维.
例5(2007年第6题) Alf、Beth和Gemma三人坐在同一房间里,他们中有一人只说真话、一人总说谎话、另一人有时说谎话有时说真话.在下列情形中,请你确定每个人话语的真实性.(i)假设Alf说“我总说谎”,Beth说“对,Alf总说谎”;那么谁总说谎话?谁总说真话?简要解释你的答案.(ii)若Gemma说“Beth一直说实话”,Beth说“这是错的”;那么谁一直说谎?谁一直说真话?简要解释你的结论.(iii)假如Alf说“Beth有时说谎,有时说真话”,Gemma说“Alf一直说谎”,而Beth说“你所听到的足够判断谁一直说真话”;那么谁一直说谎?谁一直说真话?简要解释你的答案.
这是一道逻辑判断题,无需复杂的数学知识与方法,却需要进行合理的逻辑推理.通过分析、判断、推理易知,只有有时说谎话有时说真话的人才能说出“我一直说谎”,从而得出(i)中,Alf即是那个有时说谎有时说真话的人,由此推出Beth说谎,最后得知Gemma说实话.(ii)在(i)同样的前提下,知道说真话的那个人不能说其他人只说真话,所以Gemma不是一直说真话的那个人;如果Gemma的话是对的,这与Beth说“这是错的”矛盾,所以Gemma的话为假,即Beth不只说真话,于是可知Alf一直说真话、Gemma一直说谎.(iii)是最佳可能问题,设表示Alf只说真话,Beth总说谎话,Gemma有时说谎话有时说真话(以下雷同),考虑全部6种情形;Alf的陈述排除和,Gemma的说法又排除,“没有”足够的信息判断谁一直说真话,故Beth说谎,排除、,只剩,即Alf只说真话、Gemma总说谎话.
从2007—2014年试题看,每年第6题都会出现类似试题,要求判断涉及“逻辑学家”等简单情境的说话真假、游戏真假问题,这似乎与大纲不符,其实这是考核基本的数学素养——逻辑推理能力,这是进一步学习数学与计算机科学所必需的.在中国,逻辑推理问题、数字与图形推理、奇偶性分析、容斥原理、抽屉原理、极端原理等,大多属于数学竞赛范畴(初中数学竞赛大纲就有明确规定),公务员考试也有所涉猎,但出现在正常的中小学数学课堂教学与考试中还不多见.
3 MAT命题技术的借鉴意义
2014年9月《国务院关于深化考试招生制度改革的实施意见》明确指出,“自主招生主要选拔具有学科特长和创新潜质的优秀学生.……试点高校要合理确定考核内容,不得采用联考方式或组织专门培训.”在这一新背景下,自主招生如何甄别数学英才的独立思考能力与解决问题能力?MAT命题技术提供了一个值得借鉴的可行路径.
首先,分层设计试题,为数学英才发展营造良性环境、拓展成才渠道.多年来,中国数学英才的主要培养模式是数学竞赛,实践中带有或多或少的功利性而备受社会质疑[10],恢复或回归数学竞赛之数学英才培育本质,拓宽数学英才培育之数学竞赛“华山一条道”,优化中国现行数学课程标准与教材,使学生聚焦核心数学,从日常教学中发现与培育范围更广、数量更多的数学英才,并通过高校自主招生(数学)考试如MAT的成功模式予以选拔,使之成为未来STEM(科学、技术、工程、数学)等领域的国家栋梁,是当下亟待解决的迫切问题[11~15].因此,汲取MAT的命题技术,根据专业需求分层设计数学试题,如有可能可否建立更加专业的考试项目,为选拔数学英才服务,改进目前重点大学自主招生(数学)考试无专业针对性,缺乏公开透明而持续稳定的数学考纲等弊端,不失为一条行之有效的方法.
其次,题型题量相对稳定,保持运算量与思维量的和谐统一.运算量是控制试卷难度的主要手段,如何协调运算量与思维量的合理比例至关重要,需要正确处理思辨与算法的关系;思辨是思想的源泉,离开了思辨,创造性无从谈起,分析问题的过程往往蕴含着许多思辨因素,数学教学与评价应引入思辨因素;数学课堂过分强调逻辑演绎能力与计算能力的培养,恰恰忽略了思辨能力的培养.弗赖登塔尔的《作为教育任务的数学》一书就给出若干值得称道的例子,比如:“设有白酒与红酒各一杯,两者份量相同.现从白酒中舀一匙羹放入红酒杯中,调匀后,舀回一匙羹放入白酒中。问白酒杯中所含红酒是否少于红酒杯中所含的白酒?”事实上两种含量一样多,其解题思路无外乎两种:算法求解和思辨求解.前者先设酒杯、匙羹的容量分别为和,后列出方程求解,过程冗繁、容易出错;后者考虑到两杯最终所盛液体份量相同,分离各杯中的红酒、白酒,则白酒杯中的红酒来自红酒杯中所失,反之亦然,答案自明.
第三,创设试题情境,强调数学理解,考核创新潜质.这是目前国内外包括MAT在内各类数学选拔性考试的共有特点与趋势,其目的是考核学生的数学阅读能力,学会数学阅读,是数学教育追求的重要目标之一.数学阅读能力是指从数学公式、图形、符号、文字等数学材料中提取信息的心理过程能力,其核心是数学现场阅读理解能力——面对新情境,能够数学现场(临场)地阅读、理解与运用数学概念、原理解决数学问题的能力,亦即现场学习数学知识、现场解决数学问题,也就是数学上的“可持续发展能力”.与语文、外语等自然语言一样,作为科学语言的数学也承担着发展学生科学阅读等数学素养的任务[16~17].
[1] Gibb N. Reforming Education through International Evidence [EB/OL]. https://www.gov.uk/government/speeches/ nick-gibb-reforming-education-through-international-evidence, 2015-01-23.
[2] 陈昂,任子朝.英国数学英才选拔考试——第六学期数学考试简介[J].数学教育学报,2012,21(4):64-67.
[3] MAT. Specimen and Past Tests [EB/OL]. https://www.maths.ox.ac.uk/study-here/undergraduate-study/maths-admissions -test, 2015-01-18.
[4] 龚益红.英国GCE A-Level数学课程之核心数学(Core Mathematics)模块解析[J].当代教育论坛,2011,(11):84-85.
[5] 王奋平,喻平.英国高中数学教材知识整体结构设计研究——以CIE考试委员会A水平数学教材为例[J].数学教育学报,2013,22(5):32-36.
[6] 王奋平.英国两种高中数学教材比较研究——以英国Edexcel数学课本和CIMT数学课本复数为例[J].数学教育学报,2013,22(2):76-80.
[7] 王奋平.中英高中数学教材复数内容比较研究——以英国AQA数学课本和人教版A版数学课本为例[J].数学教育学报,2011,20(3):83-86.
[8] 王奋平.中英高中数学教材比较研究——以英国AQA考试委员会与北师大版高中数学教材平面向量为例[J].数学教育学报,2011,20(6):51-55.
[9] 卢建川,廖运章,王华娇.英国数学英才选拔考试MAT综合难度分析[J].数学教育学报,2015,24(6):31-34.
[10] 廖运章.美国基于CCSSM的高中数学课程设计模式[J].课程·教材·教法,2012,(9):113-121.
[11] 李亚玲,张英伯.数学英才教育的国际比较[J].数学教育学报,2011,20(2):102.
[12] 倪明,熊斌,夏海涵.俄罗斯高中课程改革的特色——数学课程普通教育与英才教育并举[J].数学教育学报,2010,19(5):12-16.
[13] 游安军.也论中国数学竞赛的教育性质——与罗增儒先生商榷[J].数学教育学报,2009,18(1):48-51.
[14] 游安军.如何正确认识“奥数”的教育价值[J].数学教育学报,2009,18(5):69-71.
[15] 张英伯,李建华.英才教育之忧——英才教育的国际比较与数学课程[J].数学教育学报,2008,17(6):1-4.
[16] 何小亚.学生“数学素养”指标的理论分析[J].数学教育学报,2015,24(2):13-20.
[17] 桂德怀,徐斌艳.数学素养内涵之探析[J].数学教育学报.2008,17(5):22-24.
Analysis on Propositions Technology of Mathematics Admissions Test (MAT) in British Mathematical Talent Recruitment Examination
LIAO Yun-zhang1, WANG Hua-jiao2
(1. College of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China;2. Dongjiang Middle School Affiliated to Guangzhou University, Guangdong Heyuan 517500, China)
The Mathematics Aptitude Test (MAT) is one of the British mathematical talent recruitment examination, it also is a pre-interview test for applicants to the University of Oxford’s undergraduate courses in Mathematics, Computer Science and their joint schools. The mathematical knowledge and techniques required to do the questions are taken from a syllabus roughly corresponding to the C1 and C2 modules from A-level maths, though the questions are set more variously than A-level questions. It aims to test the depth of mathematical understanding of a student in the fourth term of their A-levels (or equivalent) rather than a breadth of knowledge. TMA’s propositions is characterized by: reducing the calculation cost, a variety of methods to solve problems; designing items in layered and progressively, to test applicant’s mathematical inquiry ability; building the new situation and penetrating mathematical modeling thought, to estimate applicant’s information processing ability; according to the professional, to distinguish the different mathematical ability of applicants.
mathematical talent; University of Oxford; Mathematics Admissions Test (MAT); propositions technology
[责任编校:张楠]
G633.6
A
1004–9894(2016)03–0034–04
2016–01–09
广东省高校2014年度“创新强校工程”特色创新项目(教育科研类)——英国GCSE与GCE-AS/A数学“社会化一年多考”机制研究(2014GXJK058);广州市高等学校第六批教育教学改革立项项目——基于卓越数学教师培养的《数学教学设计》课程改革与实践研究(2014-4);广州市教育科学“十二五”规划2013年度课题——中小学幼儿园数学课程标准的国际比较研究(2013A012)
廖运章(1964—),男,仫佬族,广西罗城人,教授,主要从事数学课程与教学论研究.

