BIFURCATIONS OF TRAVELING WAVE SOLUTIONS OF INTEGRABLE EVOLUTION EQUATIONS FOR SURFACE WAVES IN DEEP WATER

MO Da-long，LU Liang，2，GUO Xiu-feng

(1.School of Sciences，Hezhou University，Hezhou 542899，China）

(2.Guangxi Key Laboratories of Hybrid Computation and Integrated Circuit Design Analysis，Nanning 530006，China）

BIFURCATIONS OF TRAVELING WAVE SOLUTIONS OF INTEGRABLE EVOLUTION EQUATIONS FOR SURFACE WAVES IN DEEP WATER

MO Da-long1，LU Liang1，2，GUO Xiu-feng1

(1.School of Sciences，Hezhou University，Hezhou 542899，China）

(2.Guangxi Key Laboratories of Hybrid Computation and Integrated Circuit Design Analysis，Nanning 530006，China）

In this paper，we investigate the traveling wave solutions of a small-aspect-ratio wave equation and an integrable evolution equation for surface waves in deep water.By applying the qualitative theory of differential equations，we analyze the phase portraits of the traveling wave systems and obtain the exact explicit representations of solitary wave solutions.

traveling wave solutions；bifurcations of phase portraits；integrable systems；surface waves equations

2010 MR Subject Classification：35Q51；35C07；37G10

Document code：AArticle ID：0255-7797（2016）05-0963-12

1 Introduction

In order to describe the dynamics of monochromatic surface waves in deep water，a asymptotic model for small-aspect-ratio wave was derived in［1］as follows

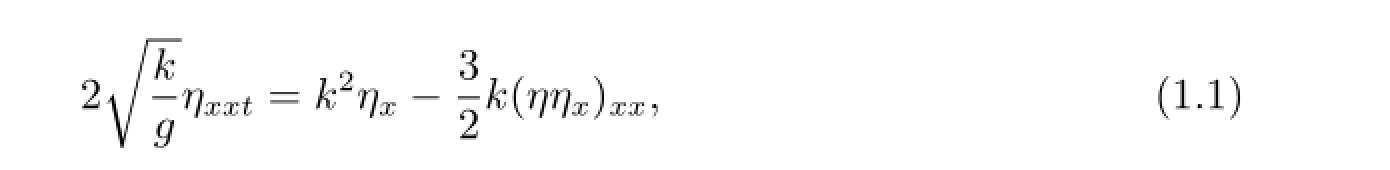
where g is the gravitation constant and k is wave vector.The equation（1.1）has a kdependent coefficient and it can be considered as belonging to both of the two categories：that of Korteweg-de Vries models（KdV，modified KdV，Benjamin-Bona-Mahony-Peregrine，Camassa-Holm，etc.）describing evolutions of wave profiles and that of NLS-type equations（modified NLS［2］，Davey-Stewartson［3］，etc.）describing modulation of wave profiles and having k-dependent coefficients.Moreover，in order to find a steep rotational Stokes wave，paper［1］also start with equation（1.1）in the frame as

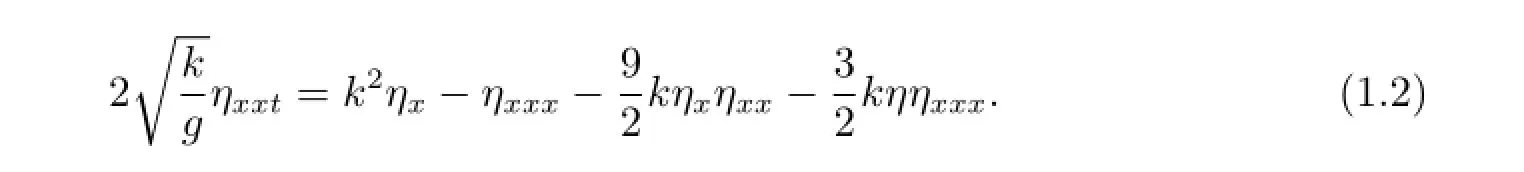
In this paper，since（1.1）and（1.2）are meaningful equations for surface waves in deep water，we will employ the bifurcation method and qualitative theory of dynamical systems ［4］to investigate these equations.The phase portraits and the explicit expressions of the bounded traveling wave solutions for the equations will obtained in the paper.To the best of our knowledge，bifurcations of traveling wave solution for above equations have not yet been considered.

It is well known that traveling waves propagation in nonlinear media was the subject of intense investigations in recent years.The study of nonlinear wave equations and their solutions were of great importance in many areas of physics（see［5-9］and the references therein）.Traveling wave solution is an important type of solutions for the nonlinear partial differential equations（NLPDEs）which were found to have a variety of traveling wave solutions（see［10，13，14，30，32］）.

In recent years，various powerful methods were developed to construct traveling wave solutions of nonlinear partial differential equations，such as the trigonometric function series method［15］，the modified mapping method and the extended mapping method（see［16］），theexpansion method（see［17，18］），the homogeneous balance method（see［19，20］），the tanh and extended methods（see［21］）and so on.Meanwhile，the bifurcation method of phase plane was developed to obtain traveling wave solutions of NLPDEs（see［22-24］）.Therefore，it is a good way to understand the behavior of traveling wave solutions of NLPDEs.What is more，breaking three solutions have attracted a great deal of interest（see［25-35］）since Konno et al.（see［37］）first reported the breaking three solutions in a nonlinear oscillation model of an elastic beam with tension.

Motivated by above mentioned works，we consider equation（1.1）and（1.2）by using the bifurcation method and qualitative theory of dynamical systems.The paper is organized as follows.In Section 2，we discuss the dynamical behavior of solutions of small-aspect-ratio wave model（1.2）and give exact parametric expressions of traveling wave solutions for the equations.In Section 3，the dynamical analysis and exact explicit representations of solitary wave solutions of an integrable evolution equation are given.At the last section，we give the conclusions of this paper.

2 Dynamical Analysis and Exact Parametric Traveling Wave Solutions

In this section，we investigate the traveling wave solutions of a small-aspect-ratio waves equation（1.1）.A breaking three solution and a family of periodic breaking three solutions are found by employing the method of the phase plane.In addition，the relationship betweenthe loop-soliton solution and the periodic loop solutions is as well investigated.The analysis may be helpful in understanding the significance of dynamical behavior of eq.（1.1）.

It is well known that a traveling wave solution of（1.1）with wave speed c is the solution having the form η=φ（ξ）with ξ=x-ct.Substituting the traveling wave solution η（x，t）=φ（x-ct）for the constant wave speed c into（1.1），we have the following ordinary differential equation

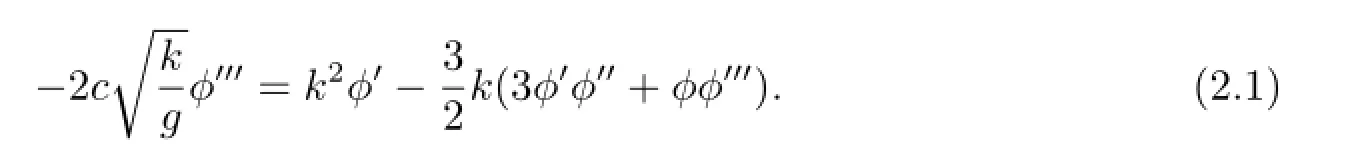
Integrating（2.1），we have

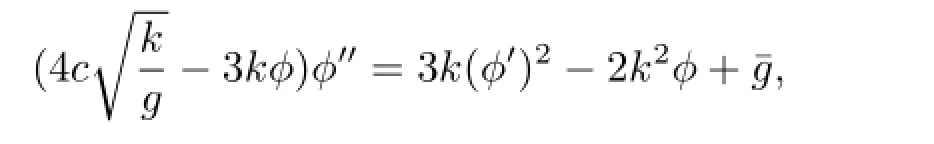
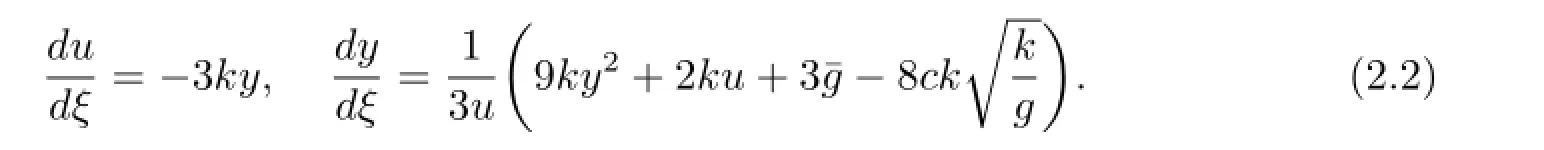
It is easy to see that system（2.2）has the first integral

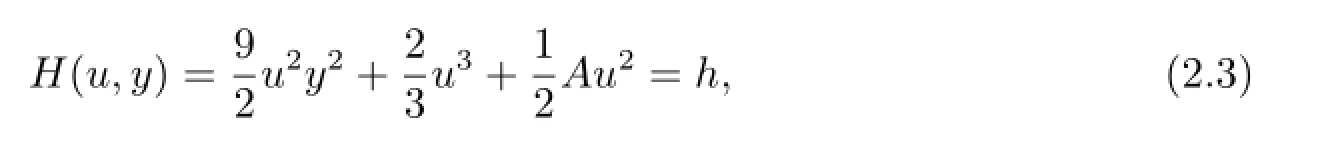
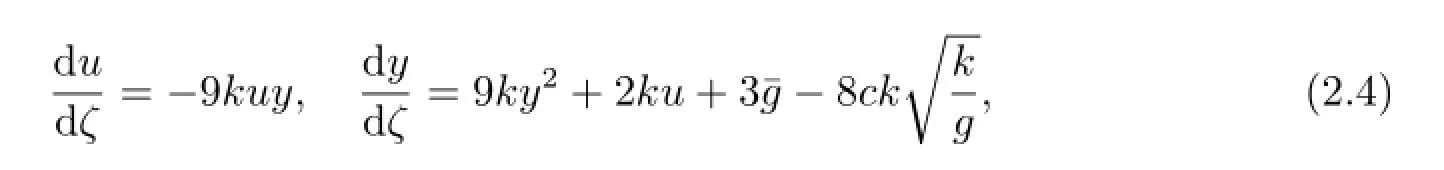
which is obtained from（2.2）by letting dξ=3udζ.System（2.4）has the same first integral H（u，y）and the same topological phase portraits as system（2.2）except for the straight line u=0.Clearly，system System（2.4）has two types of singular points of system（2.4），as follows（see Fig.1）.Using qualitative theory of differential equations［29，30］，we can easily verify the following proposition.

Proposition 2.1 Denote h0=H，the pointsand，respectively，then

Case I If A＜0，then P is a center，P1and P2are saddle points，which shown in Fig.1（a）.For h∈（h0，0）defined by（2.3），（1.1）has a family of smooth periodic wave solutions（see Fig.2（a））.For h=h0defined by（2.3），（1.1）has a unique periodic cuspon solution shown in Fig.2（b）.

Case II If A＞0，then P is saddle point（Fig.1（b））；for h=h0defined by（2.3），（1.1）has a unique breaking three solution shown in Fig.2（c）；for h∈（0，h0），there exists afamily of uncountably infinite many periodic breaking three solutions of（1.1）shown in Fig. 2（d）.Moreover，the periodic loop solutions converge to the breaking three solutions as h approaches h0.

Now，we will give the exact parametric representations of smooth traveling wave solutions，periodic cuspons，breaking three solution and periodic breaking three solutions of the small-aspect-ratio waves equation（1.1）.

（a）Smooth periodic wave solutions.

First，corresponding to Fig.1（a），when A＜0，a family of smooth periodic wave solutions of（1.1）exist，which correspond to a family of periodic orbits defined by H（u，y）=h，where h∈（h0，0）.The numerator of（2.3）can be decomposed into

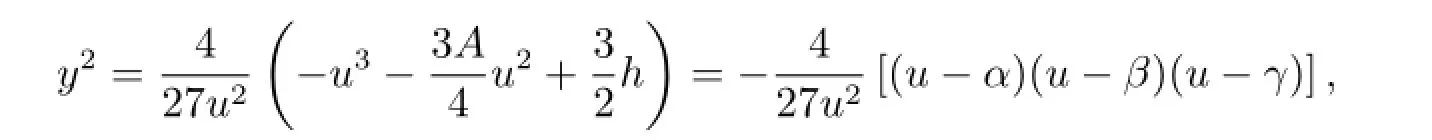
where α＞β＞0＞γ are function of c，k，g， g，which can be rigorously determined by the formula for cubic algebraic equations.Then for β＜u＜α，and by y=，we have

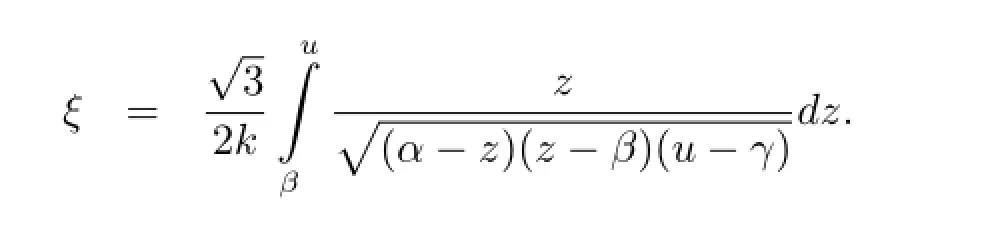
Then we obtain the following exact parametric representations of smooth periodic wave solutions of（1.1）as follows（see［36］）

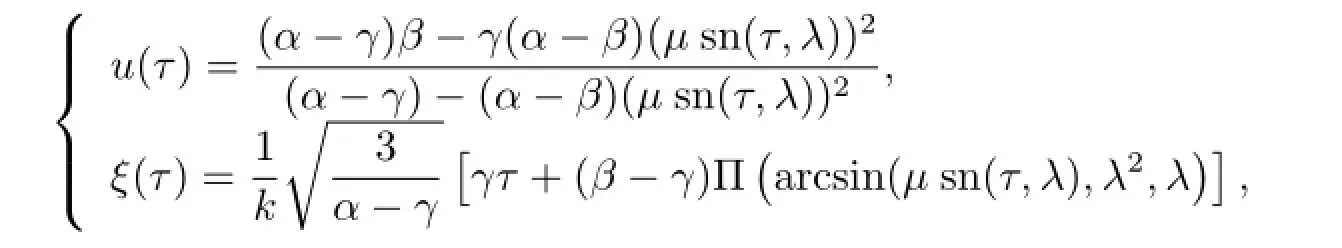
where λ2=（α-β）/（α-γ），sn（τ，λ）is Jacobian elliptic functions with the modulus λ，Π（···）is the elliptic integral of the third kind andµis a appropriate parameters.

（b）Periodic cuspons

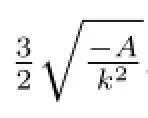
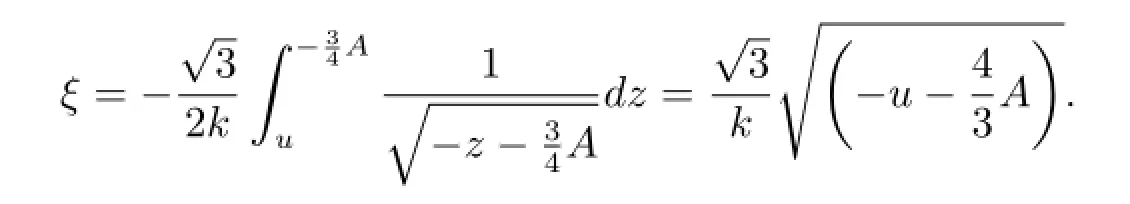
Let T=，we obtain the following periodic cuspon（see Fig.2（b））

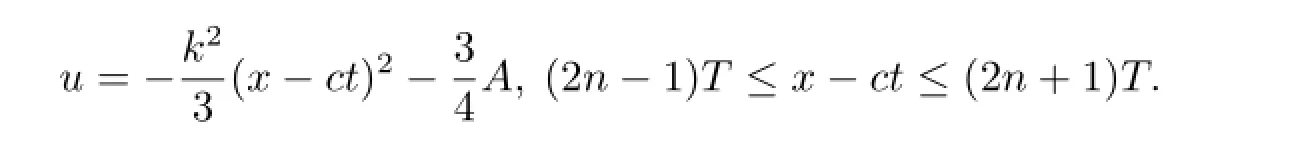
（c）Breaking three solutions

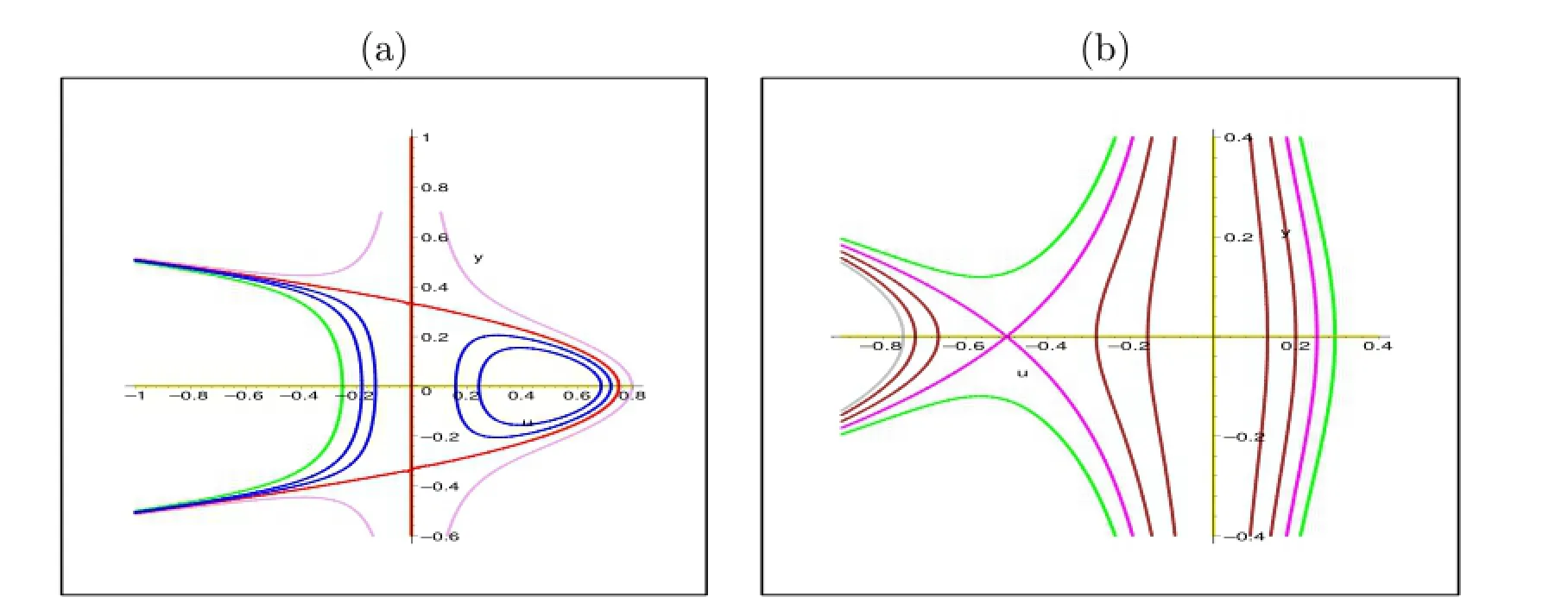
Fig.1：phase portraits of system（3.4）.（a）for A＜0，（b）for A＞0. （a）（b）

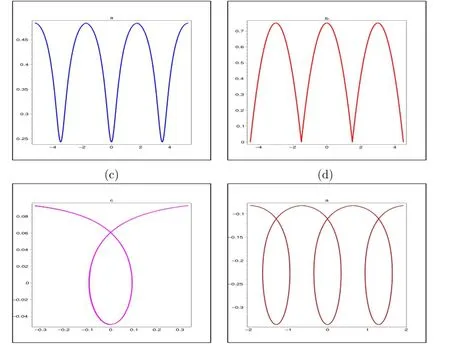
Fig.2：wave profiles.（a）smooth periodic wave solutions，（b）periodic cuspons，（c）breaking three solutions，（d）periodic breaking three solutions.

Corresponding to Fig.1（a），when A＞0 and h=h0，the equilibrium point P（-A/2，0）is a saddle point.By using the first equation of system（2.2）to perform the integration along the three orbits for the initial value u（0）=and u（0）=，respectively，we have

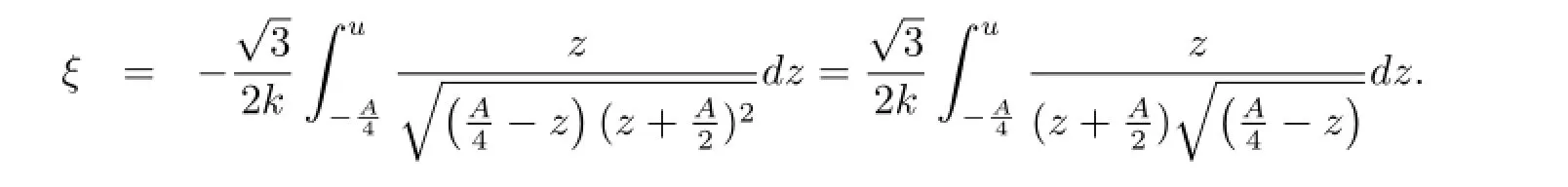
Then we obtain the following parametric representations of the traveling wave solutions of （1.1）（see Fig.2（c））

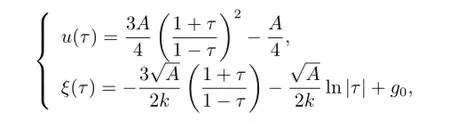
where

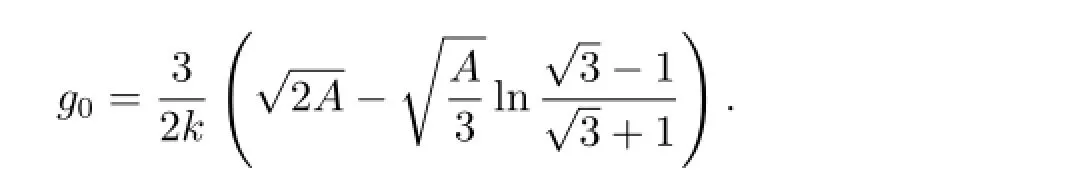
（d）Periodic breaking three solutions

Corresponding to Fig.2（d），when A＞0，the graph defined by H（u，y）=h，h∈（0，h0）consists of two open-end curves，passing through the points（β，0）and（α，0），respectively，where-A/2＜β＜0＜α.

By the algebra curve the numerator of（2.3），we have the similar representations of smooth periodic wave solutions as in（a）by doing similar procedure，we also have

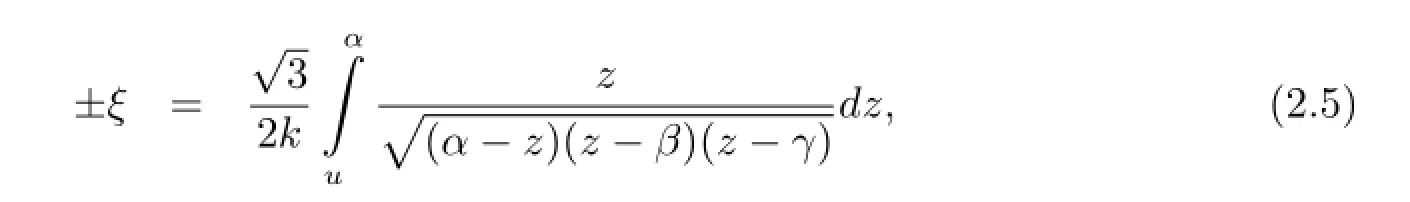
where α＞0＞β＞γ are function of c，k，g，，and we obtain the following exact parametric representations of smooth periodic wave solutions of（1.1）（see Fig.2（d））as follows

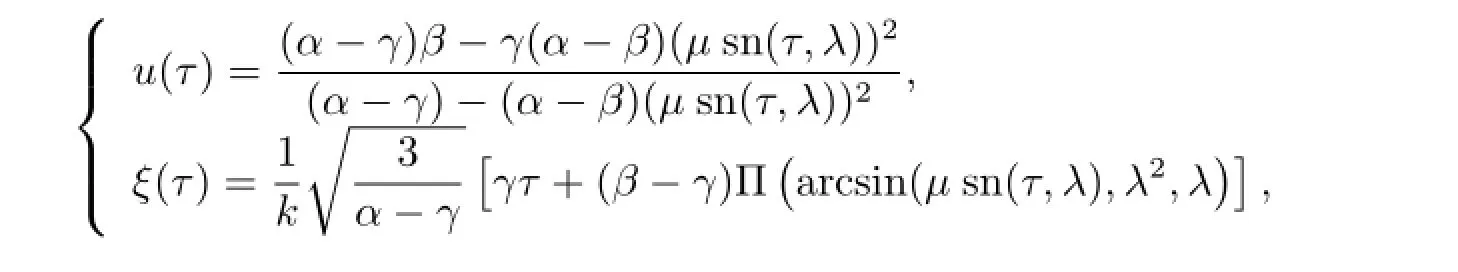
where λ2=（α-β）/（α-γ），sn（τ，λ）is Jacobian elliptic functions with the modulus λ，Π（···）is the elliptic integral of the third kind andµis a appropriate parameter.

3 Dynamical Analysis and Exact Traveling Wave Solutions of（1.2）

In this section，we investigate the periodic traveling wave solutions of（1.2）which has a great relationship with the steep rotational Stokes wave equation.Moreover，the results have some different from（1.1）.

First，by substituting η（x，t）=φ（ξ）with ξ=x-ct for the constant wave speed c into （1.2），we have the following ordinary differential equation

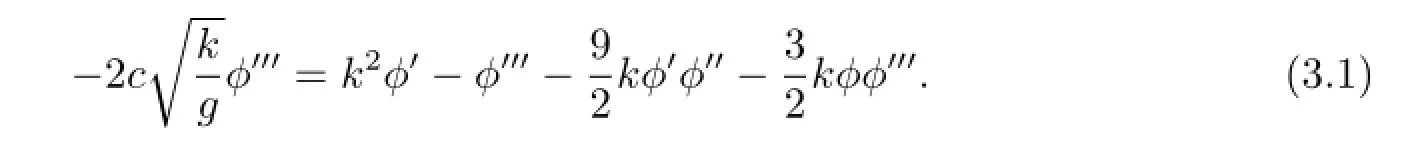
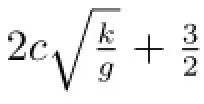
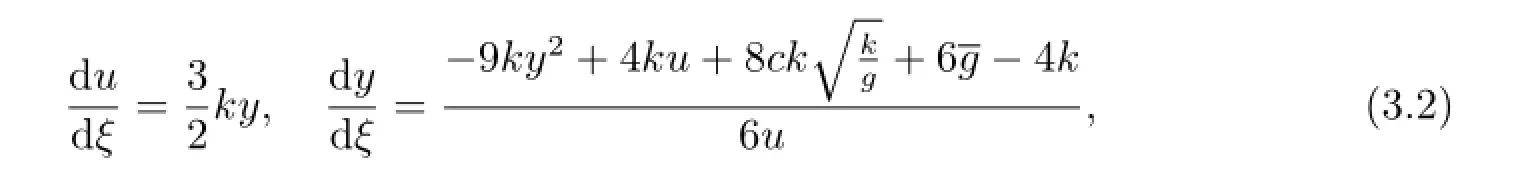
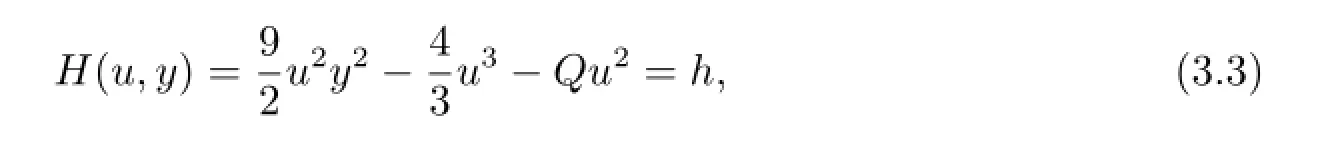
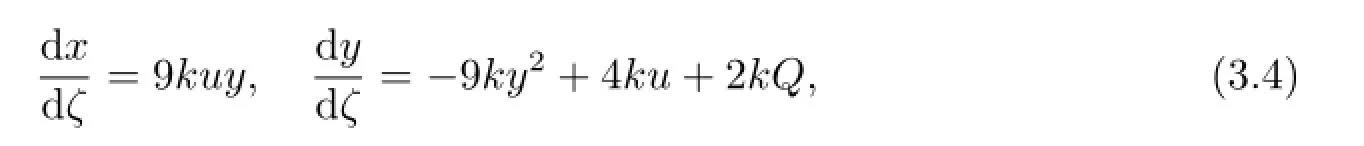
which is obtained from（3.2）by letting dξ=6udζ.System（3.4）has the same first integral H（u，y）and the same topological phase portraits as system（3.2）except for the straight line u=0.Clearly，system（3.4）also has two types of singular points，as follows（see Fig.1）.Using qualitative theory of differential equations，we can easily verify the following statement.

Proposition 3.1 Denote

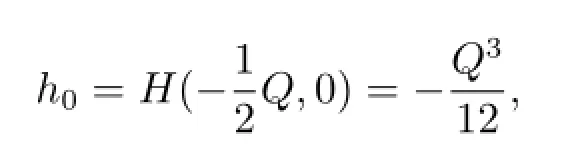
Case I If Q＞0，then P is a center；P1and P2are saddle points（see Fig.3（a））.For h∈（h0，0）defined by（3.3），（1.2）has a family of smooth periodic wave solutions（Fig.4（a））. For h=0 defined by（3.4），（1.2）has a unique periodic cuspon shown in Fig.4（b）.

Case II If Q＜0，then P is saddle points（see Fig.3（b）；For h=h0defined by（3.4），（1.2）has a unique breaking three solution which is shown in Fig.4（c）.For h∈（0，h0），there exists a family of uncountably infinite many periodic loop solutions of（1.2）shown in Fig.3（d）.Moreover，the periodic breaking three solutions converge to the breaking three solutions as h approaches h0.

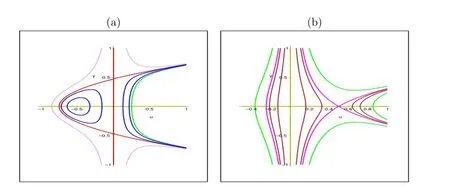
Fig.3：phase portraits of system（3.4），（a）for Q＞0，（b）for Q＜0. （a）（b）

Fig.4：（color online）wave profiles.（a）smooth periodic wave solutions，（b）periodic cuspons，（c）breaking three solutions，（d）periodic breaking three solutions.

In the following，we will give the exact representations of the smooth periodic traveling wave solutions，periodic cuspons，the breaking three solution and periodic breaking three solutions of equation（1.2）.

（a）Smooth periodic wave solutions.

Corresponding to Fig.3（a），when Q＞0，a family of smooth periodic wave solutions of （1.1）exist，which correspond to a family of periodic orbits defined by H（u，y）=h∈（h0，0），we have

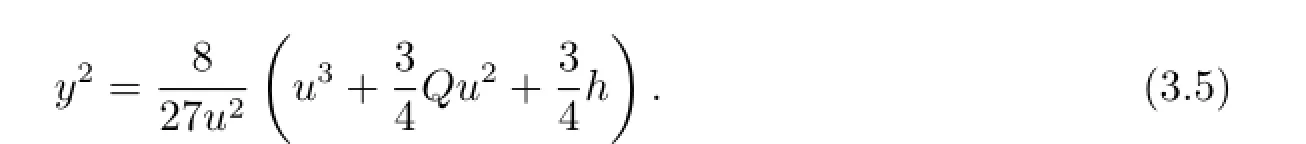
By using the first equation of system（3.2），we have

where γ＜β＜0＜α are function of c，k，g，，which can be rigorously determined by the formula for cubic algebraic equations.Then we obtain the following exact parametric representations of smooth periodic wave solutions of of eq.（1.2）

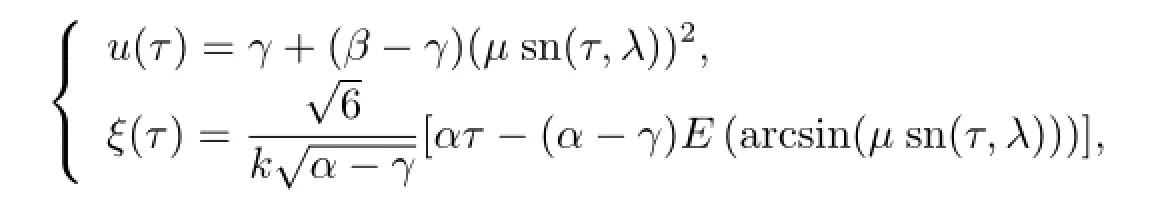
where λ2=（β-γ）/（α-γ），sn（τ，λ）is Jacobian elliptic functions with the modulus λ，E（·）is the elliptic integral of the second kind andµis a appropriate parameters.

（b）Periodic cuspons

Corresponding to Fig.3（b），when Q＞0 and h=0，a periodic cuspon of（1.2）exists，which corresponds to the heteroclinic orbits defined by H（u，y）=h=0.We have the following traveling wave solution of（1.2）

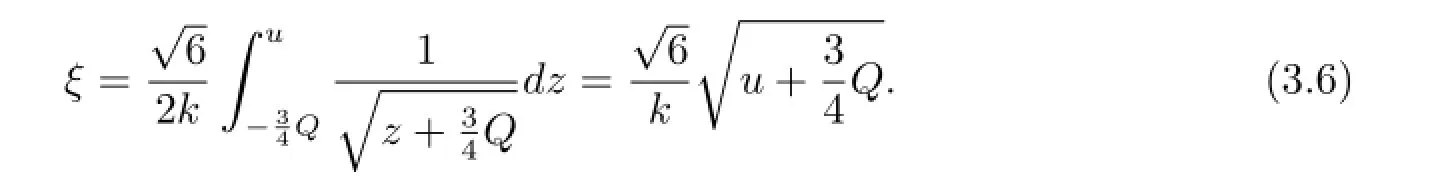
Thus we have the periodic cusp wave solutions of equation（1.2）（see Fig.4（b））

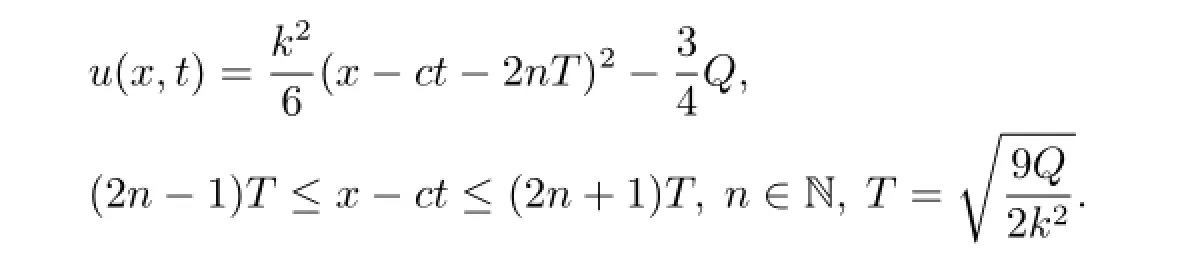
（c）Breaking three solutions

Corresponding to Fig.3（b），when Q＜0 and h=h0，the equilibrium point P（-Q/2，0）is a saddle point.By using the first equation of system（3.2）to perform the integration along the three orbits for the initial value u（0）=Q/4 and u（0）=-Q/4，respectively，we have

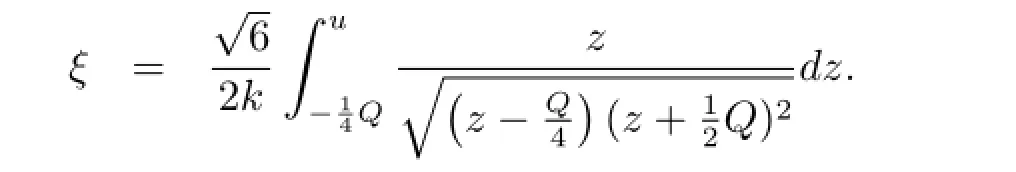
Then we obtain the following parametric representations of the traveling wave solutions of （1.2）（see Fig.4（c））

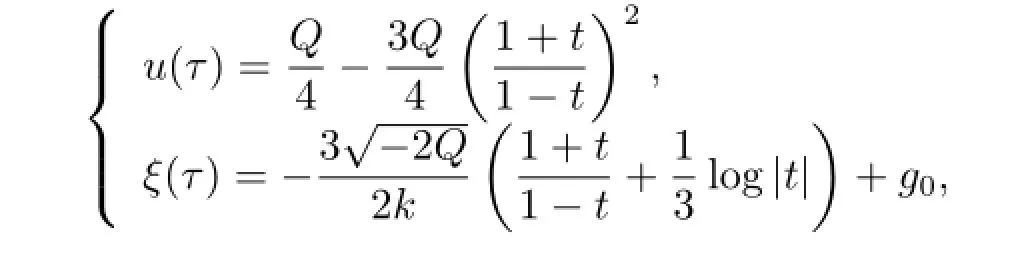
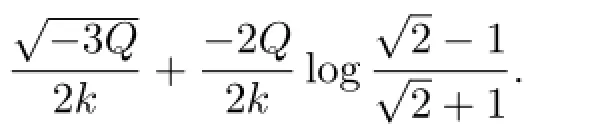
（d）Periodic breaking three solutions

Corresponding to Fig.3（b），when Q＜0 and h∈（0，h0），the graph defined by H（u，y）= h∈（0，h0）consists of two open-end curves，passing through the points（γ，0）and（β，0），respectively，where γ＜0＜β＜.By calculating，we obtain following exact parametric representations of the periodic breaking three solutions of（1.2）［see Fig.4（d）］

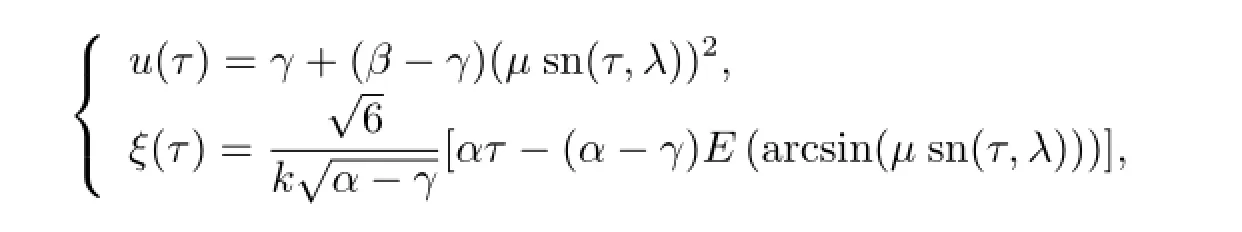
where λ2=（β-γ）/（α-γ），sn（τ，λ）is Jacobian elliptic functions with the modulus λ and µis a appropriate parameter.

4 Conclusions

In this paper，by using the qualitative theory of differential equations，a small-aspectratio wave equation（1.1）and an integrable evolution equation（1.2）for surface waves in deep water are studied.The phase portraits of the traveling wave systems are analyzed（see Fig. 1 and Fig.3）and exact explicit representations of solitary wave solutions such as smooth periodic wave solutions，periodic cuspons，breaking three solution and periodic breaking three solutions（see Fig.2 and Fig.4）are give in Section 2 and Section 3，respectively.By comparing the results of these two equations，the phase portraits and exact explicit representations of solitary wave solutions are obtained under some different parameter conditions.

References

［1］Kraenkel R A，Leblond H，Manna M A.An integrable evolution equation for surface waves in deep water［J］.Phys.A：Math.Theor.，2014，47：1-17.

［2］Dodd R K，Eilbeck J C，Gibbon J D，Morris H C.Solitons and nonlinear wave equations［M］.London：Academic，1982.

［3］Davey A，Stewartson K.On three-dimensional packets of surface waves［J］.Proc.R.Soc.Lond.A.，1974，338：101-110.

［4］Nemytskii V，Stepanov V.Qualitative theory of differential equations［M］.New York：Dover，1989.

［5］Biswas A，Yildirim A，Hayat T，Aldossary O，Sassaman R.Soliton perturbation theory for the generalized Klein-Gordon equation with full nonlinearity［J］.Proc.Rom.Acad.Ser.A Math.Phys. Tech.Sci.Inf.Sci.，2012，13：32-41.

［6］Lenells J.Traveling wave solutions of the Camassa-Holm equation［J］.J.Differ.Equ.，2005，217：393-430.

［7］Liu Yu.New type soliton solutions to Korteweg-de Vries and Benjamin-Bona-Mahony equations［J］. Chin.Phys.Lett.，2010，27（9）：090201，1-4.

［8］Razborova P，Ahmed B，Biswas A.Solitons，shock waves and conservation laws of Rosenau-KdVRLW equation with power law nonlinearity［J］.Appl.Math.Inf.Sci.，2014，8：485-491.

［9］Wazwaz A M.Multiple soliton solutions for an integrable couplings of the Boussinesq equation［J］. Ocean Eng.，2013，73，38-40.

［10］Johnpillai A G，Yildirim A，Biswas A.Chiral solitons with Bohm potential by Lie group analysis and traveling wave hypothesi［J］.Rom.J.Phys.，2012，57：545-554.

［32］Li Jibin，Qiao Zhijun.Peakon，pseudo-peakon，and cuspon solutions for two generalized Camassa-Holm equations［J］.J.Math.Phys.，2013，54：1-14.

［30］Li Jibin，Liu Zhengrong.Smooth and non-smooth traveling waves in a nonlinearly dispersive equation［J］.Appl.Math.Model.，2000，25：41-56.

［13］Zhang Lina，Chen Aiyong，Tang Jiade.Special exact soliton solutions for the K（2，2）equation with non-zero constant pedestal［J］.Appl.Math.Comput.，2011，218：4448-4457.

［14］Zhang Zaiyuna，Liu Zhenhai，Miao Xiujin，Chen Yuezhong.Qualitative analysis and traveling wave solutions for the perturbed nonlinear Schr¨odinger's equation with Kerr law nonlinearity［J］.J.Phys. A，2011，375：1275-1280.

［15］Zhang Zaiyun.New exact traveling wave solutions for the nonlinear Klein-Gordon equation［J］.Turk. J.Phys.，2008，32：235-240.

［16］Zhang Zaiyuna，Liu Zhenhai，Miao Xiu-jin，Chen Yuezhong.New exact solutions to the perturbed nonlinear Schr¨odinger's equation with Kerr law nonlinearity［J］.Appl.Math.Comput.，2010，216：3064-3072.

［17］Wang Mingliang，Li Xiangzheng，Zhang Jinliang.The）-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics［J］.Phys.Lett.A，2008，372：417-423

［18］Shehata A R.The traveling wave solutions of the perturbed nonlinear Schrdinger equation and the cubic-quintic Ginzburg Landau equation using the modified）-expansion method［J］.Appl. Math.Comput.，2010，217（1）：1-10.

［19］Wang Mingliang.Exact solutions for a compound KdV-Burgers equation［J］.Phys.Lett.A 1996，213：279-287.

［20］Fan Engui，Zhang Hongqing.A note on the homogeneous balance method［J］.Phys.Lett.A，1998，246：403-406.

［21］Duffy B R，Parkes E J，Travelling solitary wave solutions to a seventh-order generalized KdV equation［J］.Phys.Lett.A，1996，214：271-272.

［22］Tang Minying，Yang Chengxi.Extension on peaked wave solutions of CH-γ equation［J］.Chaos Solitons Fractals，2004，20：815-825.

［23］Li Jibin，Zhang Lina.Bifurcations of traveling wave solutions in generalized Pochhammer-Chree equation［J］.Chaos Solitons Fractals，2002，14：581-593.

［24］Liu Zhengrong，Qian Tifei.Peakons of the Camassa-Holm equation［J］.Appl.Math.Modeling，2002，26：473-480.

［25］Abbasbandy S，Parkes E J.Solitary smooth hump solutions of the Camassa-Holm equation by means of the homotopy analysis method［J］.Chaos Sol.Fract.，2008，36，581-591.

［26］Chen Aiyong，Li Jibin.Single peak solitary wave solutions for the osmosis K（2，2）equation under inhomogeneous boundary condition［J］.J.Math.Anal.Appl.，2010，369：758-766.

［27］Chen Aiyong，Huang Wentao，Xie Yongan，Nilpotent singular points and compactons［J］.Appl. Math.Comput.，2014，236：300-310.

［28］Chen Aiyong，Wen Shuangquan.Double compactons in the Olver-Rosenau equation［J］.Pramana J. Phys.，2013，80：471-478.

［29］Li Jibin，Dai Huihui.On the study for singular nonlinear wave equations：Dynamical approach［M］. Beijing：Sci.Publ.House，2007.

［30］Li Jibin.Singular nonlinear travelling wave equations：Bifurcations and exact solutions［M］.Beijing：Sci.Press，2013.

［31］Jibin Li.Dynamical understanding of loop soliton for several nonlinear wave equations［J］.Sci. China Ser.A，2007，50（6）：773-785.

［32］Li Jibin，Chen Guanrong.On nonlinear wave equations with breaking loop-solutions［J］.Inter.J. Bifur.Chaos，2010，20（2）：519-537.

［33］Rosenau P，Hyman J M.Compactons：solitons with finite wavelengths［J］.Phys.Rev.Lett.，1993，70：564-567.

［34］Rong Jihong，Tang Shengqiang，Huang Wentao，Bifurcations of traverlling wave solutions for the K（n，2n，-n）equations［J］.J.Math.，2010，30：603-612.

［35］Tang Shengqiang，Tang Qinggan，Travelling wave solutions for the generalized special type of the Tzitzeica-Dodd-Bullough equations［J］.J.Math.，2009，29：27-36.

［36］Byrd P F，Friedman M D.Handbook of elliptic integrals for engineers and scientists［M］.New York：Springer，1971.

［37］Konno K，Ichikawa Y H，Wadati M，A Loop soliton Propagating along a Stretched Rope［J］.J.Phys. Soc.Jpn.，1981，50：1025-1026.

深水表面波可积发展方程的行波解与分支

莫达隆1，卢亮1，2，郭秀凤1
（1.贺州学院理学院，广西贺州542899）
（2.广西混杂计算与集成电路设计分析重点实验室，广西南宁530006）

本文研究了small-aspect-ratio波方程和深水表面波可积发展方程的行波解问题.利用微分方程定性理论的方法，分析了行波系统的相图分支，获得了孤立波解的精确表达式.

行波解；相图分支；可积系统；表面波方程

MR（2010）主题分类号：35Q51；35C07；37G10O175.29

date：2014-09-04Accepted date：2015-04-07

Supported by National Natural Science Foundation of China Grants（11461021）；National Natural Science Foundation of Guangxi Grant（2014GXNSFAA118028）；Scientific Research Foundation of Guangxi Education Department（KY2015YB306）；the open fund of Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis（HCIC201305）；Scientific Research Project of Hezhou University（2012PYZK02；2015ZZZK16）；Guangxi Colleges and Universities Key Laboratory of Symbolic Computation and Engineering Data Processing.

Biography：Mo Dalong（1970-），male，born at Mengshan，Guangxi，associate professor，major in probability and statistics，differential equations.

Lu Liang.