一种基于KL分离度的改进矩阵CFAR检测方法

赵兴刚 王首勇



一种基于KL分离度的改进矩阵CFAR检测方法

赵兴刚*王首勇

(空军预警学院 武汉 430019)

矩阵CFAR检测器是根据信息几何理论提出的，但其恒虚警特性没有从理论上得到分析，且检测性能也有待进一步提高。该文首先根据矩阵流形上正态律的概念从理论上推导了矩阵CFAR检测器的恒虚警特性，并在此基础上，利用积累性能更好的KLD(KULLBACK-LEIBLER Divergence)代替测地线距离，提出了一种改进的矩阵CFAR检测器。最后通过仿真实验验证了改进方法具有更好的检测性能。

信息几何；恒虚警检测；统计流形；测地线距离；KULLBACK-LEIBLER分离度(相对熵)

1 引言

信息几何是近年来刚发展起来的新兴学科，文献[1]于1945年提出用Fisher信息矩阵来定义黎曼度量，开启了统计的几何学研究。1972年， 文献[2]引入了一个仿射联络族，与此同时，文献[3]定义了统计流形的曲率概念，并指出曲率在统计推断高阶渐进理论中的基本作用。此后，文献[4,5]引入了单参数的仿射联络族，建立了统计流形的对偶几何结构，极大丰富和完善了统计的几何学理论框架，进而建立了信息几何。近年来，信息几何的理论基础不断完善，已在系统理论、神经网络和统计推断等领域得到了广泛应用[6]。

信息几何在雷达信号处理中的应用主要是文献[7-9]提出了一种矩阵CFAR检测方法，该方法利用检测单元回波协方差矩阵与参考单元协方差矩阵均值之间的测地线距离作为检测量进行检测，克服了传统PD雷达CFAR检测中多普勒处理在短脉冲序列条件下所面临的多普勒分辨率降低、能量泄露、杂波谱污染等问题，有效提高了检测性能，而且利用了矩阵流形的内在结构对矩阵均值进行了准确估计，具有更稳健的恒虚警特性。然而矩阵CFAR检测方法仍存在一些不足：(1)它没有从理论上严格分析该方法是否具有恒虚警特性；(2)测地线距离的检测性能有待进一步提高。

针对以上不足，本文首先利用矩阵流形上正态律的概念从理论上推导了矩阵CFAR的恒虚警特性，得到了检测门限的理论表达式，并在此基础上，使用积累性能更好的KULLBACK-LEIBLER分离度(KULLBACK-LEIBLER Divergence, KLD)代替测地线距离，提出了一种改进的矩阵CFAR检测器，最后通过仿真实验验证了改进方法的检测性能。

2 矩阵流形的基础知识

设雷达中某个距离单元观测的复包络信号为

2.1 测地线距离

矩阵流形上的任意一个点都代表了对应于某一个协方差矩阵的零均值复高斯矢量分布，且在定义Fisher信息矩阵为统计流形黎曼度量的基础上，可以得到流形上任意两点之间的最短距离，称为测地线距离，矩阵流形上任意两点和之间测地线距离的表达式为[11]

2.2 矩阵的黎曼均值

通过利用测地线方程，取切向量的方向为目标函数的负梯度方向，就可以得到递推计算黎曼均值的梯度下降算法。对于矩阵流形上给定的个点，令，梯度下降算法的迭代计算表达式为

2.3 矩阵流形上的正态律

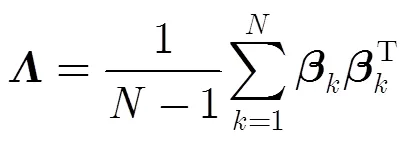
式中有

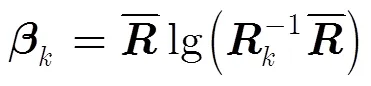
3 常规CFAR检测器面临的问题

在一般PD雷达中所采用的常规CFAR检测器属于单脉冲检测，即对单个距离单元回波信号相参积累(FFT)后，进行线性检波或平方律检波，再进行恒虚警检测，图1以CA-CFAR为例给出了其处理流程图。

图1 常规CFAR检测器

打击飞行目标要有更短的反应时间。

然而传统CFAR还不能满足这些新的处理要求，尤其是在非均匀或强杂波背景下，传统CFAR检测的恒虚警性能是较差的，另外对于多功能和多任务雷达，是通过使用较短的脉冲序列来减少时间预算，以获取更快的处理速度，然而，此时FFT处理会面临以下问题：(1)多普勒分辨率下降，如果目标多普勒频率位于两个多普勒滤波器之间，会发生能量泄露；(2)在地、海杂波等背景下，杂波谱会散布到目标所在的多普勒滤波器中，致使检测性能下降。

4 矩阵CFAR检测器

为了克服常规CFAR存在的以上问题，文献[7-9]基于信息几何理论，提出了一种在强非均匀杂波背景下，且当雷达CPI脉冲数较少时，更加有效和稳健的矩阵CFAR检测器。其主要思想是：首先根据雷达观测数据计算参考单元和检测单元的协方差矩阵，然后将这些矩阵统一看做矩阵流形上的点，进而用检测单元协方差矩阵与参考单元协方差矩阵均值之间的测地线距离作为检测量与门限比较，实现目标检测，其处理流程如图2所示。

图2 矩阵CFAR检测器

从理论上讲，协方差矩阵包含了回波的所有信息，因而直接用矩阵进行检测就避免了常规CFAR中CPI脉冲数较少时FFT的性能损失；在恒虚警特性方面，流形上的矩阵均值与传统CFAR中用到的杂波功率的一阶估计(算术平均)相比，是利用了流形上的内在结构对均值进行估计，受杂波环境影响更小，因而在一些强的非均匀杂波背景下，具有更好的稳健性。

文献[7]为改善常规CFAR存在的问题而提出了上述的矩阵CFAR检测器，但矩阵CFAR只是给出了检测策略，对于能否真正具有恒虚警特性没有进行理论分析，也就没有给出检测门限的理论值；并且流形上距离定义有多种，利用测地线距离进行检测无法保证是最优的。

5 基于KLD的矩阵CFAR检测器

针对上节分析的矩阵CFAR存在的不足，本节通过利用矩阵流形上的几何性质以及内蕴的统计特性逐一进行了分析和解决，并提出了一种改进的矩阵CFAR检测器。

5.1 恒虚警特性及门限

图3给出了矩阵CFAR检测器在流形上的示意图，在流形上参考单元的协方差矩阵可以看做流形上的一个粒子群，那么矩阵CFAR就是通过比较与这个粒子群中心点之间距离来实现检测的。在没有目标时，根据矩阵流形上的广义正态律，包括在内的所有点都服从一个如式(6)所示的广义正态分布。从图3可以得出，式(7)所示的检测器可以等价于。

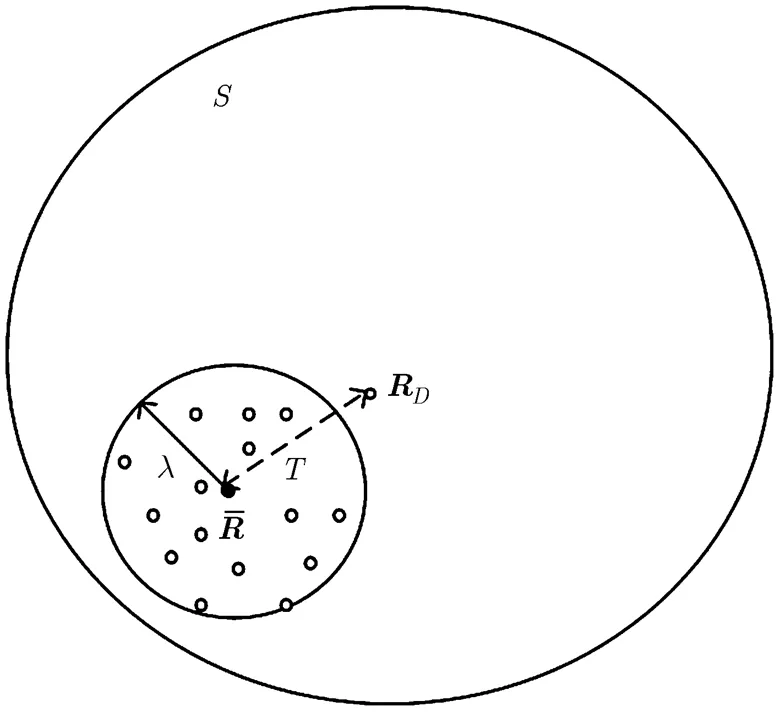
图3 矩阵CFAR在流形上的示意图

价于杂波功率的估计，因而矩阵CFAR检测器是具有恒虚警特性的。

5.2 用KLD代替测地线距离

然后，我们从信息几何的角度来解决该检测问题，在矩阵流形上，两种假设分布分别为

式中，det和tr分别代表矩阵的行列式和迹。由观测数据得到的分布为，协方差矩阵由计算得到，则根据式(13)可得流形上到和的KLD分别为

则可用KLD在信息几何框架下定义一种距离检测器[6]为

如果将式(16)中的KLD用式(3)所示的测地线距离替换，则可得基于测地线距离的距离检测器为

从直观上很难得到式(11)，式(16)，式(17)三者之间的关系，因此采用蒙特卡洛方法对3种方法的检测性能进行比较，图4给出了似然比检测(LRT)、基于KLD的距离检测器(KDD)、基于测地线距离的距离检测器(GDD)3种检测方法的性能比较曲线。

从图中可以看出，KDD与LRT检测是完全等价的，在给定虚警概率的前提下，具有最优的检测性能，而GDD的性能要差于KDD和LRT检测。在距离检测器中，距离本质上是代表了一种能量积累的方式，由检测性能的比较可以得出，KLD比测地线距离具有更好的积累性能。

实际上，通过比较式(7)和式(17)可以发现，矩阵CFAR检测在本质上可以等价于“一半”的GDD。在GDD中，假设和是已知的，而在实际应用中，这两者是很难得到的，矩阵CFAR首先舍去了式(17)中，就不需要用到，再者类比于常规CFAR检测的思想，通过计算参考单元杂波协方差矩阵的均值对进行估计，因而矩阵CFAR更便于工程应用。根据矩阵CFAR与GDD之间的关系，则同样可以利用“一半”的KDD定义一种新的矩阵CFAR检测器，即利用KLD代替式(7)中的测地线距离，

上文已经提到，KLD比测地线距离具有更好的积累性能，因而式(18)所示的基于KLD的矩阵CFAR检测器会比文献[7-9]中的矩阵CFAR具有更好的检测性能。

6 仿真实验

本节使用SIRP法仿真产生K杂波来模拟目标检测背景，对常规CFAR，矩阵CFAR和改进的矩阵CFAR 3种方法的检测性能进行比较分析。

针对第3节分析的常规CFAR在杂波背景和短脉冲序列条件下存在的杂波谱展宽、多普勒分辨率降低和能量泄露等问题，我们设置4种仿真场景，即场景1：不存在杂波谱展宽和能量泄露的影响；场景2：只存在能量泄露的影响；场景3：只存在杂波谱展宽的影响；场景4：杂波谱展宽和能量泄露的影响都存在。

4种场景的设置可以通过调节K杂波仿真中的杂波谱宽度和目标多普勒频率来实现。场景1和2的设置中，我们令K杂波仿真中的功率谱3 dB带宽为40 Hz，场景3和场景4对应为80 Hz，两种带宽的功率谱密度曲线如图5所示。

能量泄露的影响是由多普勒滤波器组和目标多普勒频率共同决定的，因为脉冲重复频率为1000 Hz，多普率滤波器的个数为8个，则可以令场景1和场景3中，场景2和场景4中，图6以多普勒滤波器组的形式给出了4种场景的示意图。

然后我们利用常规CFAR、矩阵CFAR和改进的矩阵CFAR 3种方法分别对每一种场景下的仿真目标信号进行检测，信杂比范围设置为

从图7可以看出，场景1中，由于没有杂波谱展宽和能量泄露的影响，FFT能使目标信号能量有效积累，且目标所在的多普勒滤波器中杂波能量微弱，此时常规CFAR的性能是较好的；场景2中，受到了能量泄露的影响，即在两个多普勒滤波器之间，此时常规CFAR中检测量对应的多普勒滤波器只积累了一部分信号能量，因而检测性能下降；场景3中，杂波谱展宽，即目标信号所在的多普勒滤波器也散布了一部分杂波能量，使得检测性能下降；场景4中两种影响都有，因而检测性能是最差的。矩阵CFAR和改进的矩阵CFAR都是直接利用协方差矩阵进行检测，因而上述两个方面的影响是相对较小的，除了在场景1中，常规CFAR的检测性能较好以外，在其他3种场景下，矩阵CFAR的性能有优势，但在场景2和场景4中不明显，而改进的矩阵CFAR的检测性能要明显优于矩阵CFAR和常规CFAR，这也验证了本文所提出的改进矩阵CFAR检测器的有效性。

矩阵CFAR和改进的矩阵CFAR都是利用了矩阵流形的内在结构对矩阵均值进行估计，因而它们的另一优势是稳健性，即在不同的背景下检测性能变化的程度相对较小，我们通过将3种方法在4种场景下的检测性能曲线放在一起比较，如图8所示，可以看出常规CFAR的检测性能在不同场景下的波动程度要更大，而矩阵CFAR和改进的矩阵CFAR具有更稳健的检测性能。

7 结束语

矩阵CFAR是信息几何理论在雷达目标检测中的一项重要应用，在一些场景下具有比传统方法更好的检测性能和恒虚警特性。本文在前人研究的基础上，对矩阵CFAR进行了更深入的理论分析，提出了一种改进方法，进一步提高了性能，并通过仿

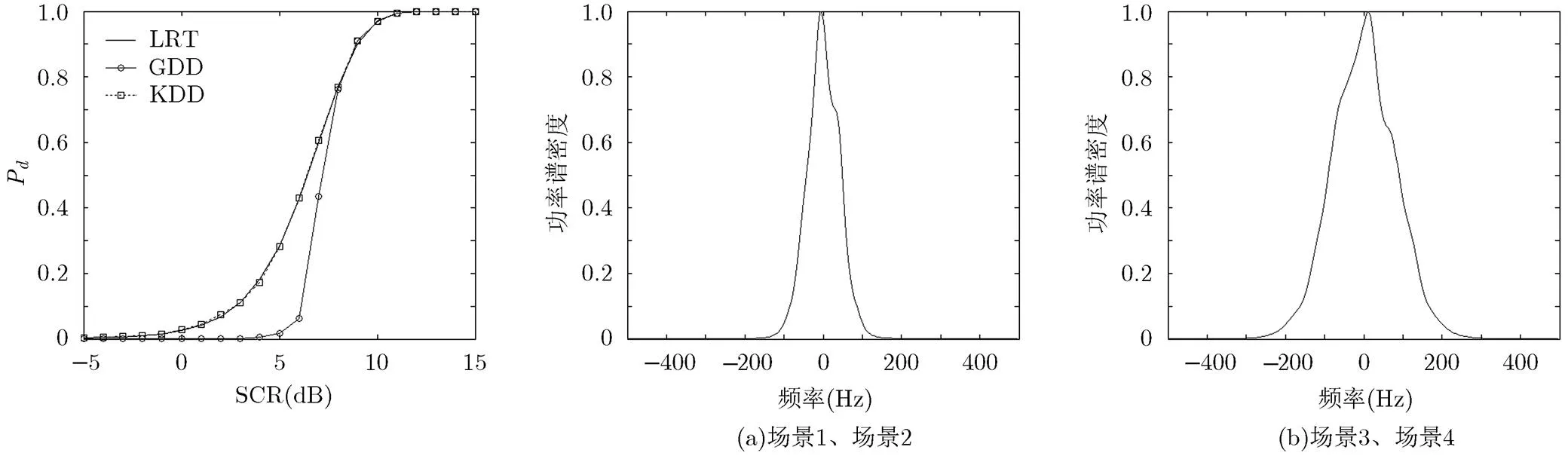
图4 LRT, KDD, GDD 3种方法检测性能比较 图5 杂波的功率谱密度曲线

图6 4种仿真场景示意图

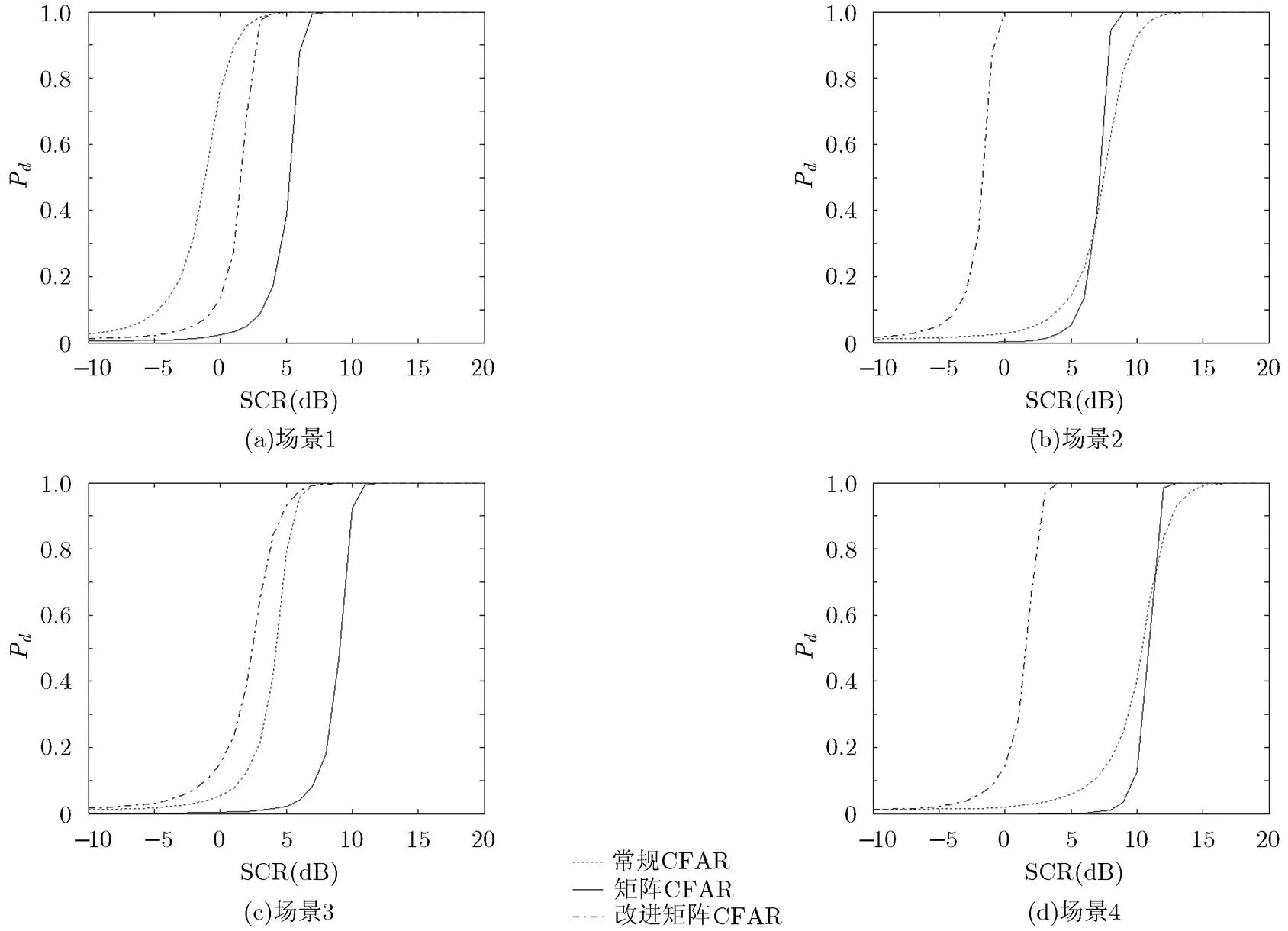
图7 检测性能曲线

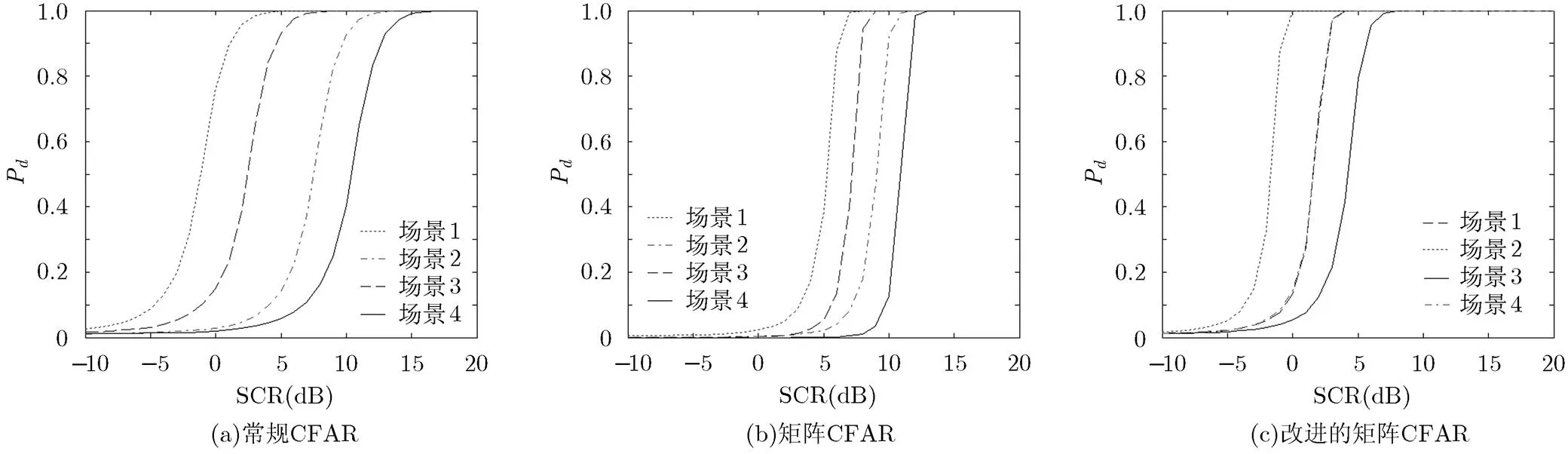
图8 3种方法在4种场景下的检测性能比较

真实验进行了验证。然而，除此之外，矩阵CFAR仍有许多问题需要继续深入研究，如矩阵流形本身是假定杂波序列服从零均值高斯分布的，那么在强非高斯杂波背景下，由于杂波类型的不准确，也会导致性能的下降[16]，这是在以后的研究中需要着重解决的问题。

[1] RAO C. Information and accuracy attainable in the estimation of statistical parameters[J]., 1945, 37(2): 81-91.

[2] CHENTSOV N N. Statistical Decision Rules and Optimal Inference[M]. Rhode Island, USA: American Mathematical Society, 1982: 55-60.

[3] EFRON B. Defining the curvature of a statistical problem (with applications to second order efficiency)[J]., 1975, 3(6): 1189-1242.

[4] AMARI S and NAGAOKA H. Methods of Information Geometry[M]. New York: Oxford University Press, 2000: 87-96.

[5] MARCELO P, Hadj B, and STEVE M.Exploiting information geometry to improve the convergence properties of variational active contours[J]., 2013, 7(4): 700-707.

[6] 赵兴刚, 王首勇. 雷达目标检测的信息几何方法[J]. 信号处理, 2015, 31(6): 631-637.

ZHAO Xinggang and WANG Shouyong. Information geometry method of radar target detection[J]., 2015, 31(6): 631-637.

[7] BARBARESCO F. Radar detection for non-stationary time-Doppler signal based on Fréchet distance of geodesic curves on covariance matrix information geometry manifold [C]. 14th International Radar Symposium, German, 2013: 307-312.

[8] LE Y, ARNAUDON M, and BARBARESCO F. Riemannian median, geometry of covariance matrices and radar target detection[C]. 7th European Radar Conference, Paris, 2010: 415-418.

[9] BARBARESCO F. Radar detection using Siegel distance between autoregressive processes, application to HF and X-band radar[C]. IEEE Radar Conference, Rome, Italy, 2008: 523-530.

[10] 孙华飞, 彭林玉, 张真宁. 信息几何及其应用[J]. 数学进展, 2011, 40(3): 257-269.

SUN Huafei, PENG Linyu and ZHANG Zhenning. Inforamtion geometry and its application[J]., 2011, 40(3): 257-269.

[11] AMARI S. Information geometry of positive measures and positive-definite matrices: decomposable dually flat structure [J]., 2014, 16(5): 2131-2145.

[12] BARBARESCO F. Information Intrinsic Geometry Flows[C]. MaxEnt’06 Conference, Paris, 2006: 133-146.

[13] LENGLET M and ROUSSON R. Statistics on the manifold of multivariate normal distributions: Theory and application to diffusion tensor MRI processing[J]., 2006, 25(3): 423-444.

[14] 郑作虎, 王首勇. 基于Alpha稳定分布杂波模型的雷达目标检测方法[J]. 电子与信息学报, 2014, 36(12): 2963-2968. doi: 10.3724/SP.J.1146.2014.00072.

ZHENG Zuohu and WANG Shouyong. Radar target detection method based on the alpha-stable distribution clutter model[J].&, 2014, 36(12): 2963-2968. doi: 10.3724/SP. J.1146.2014.00072.

[15] KULLBACK S. Information Theory and Statistics[M]. New York: Dover Publications, 1968: 162-188.

[16] 严俊坤, 刘红亮, 戴奉周, 等. 一种具有恒虚警性质的检测跟踪联合处理算法[J]. 电子与信息学报, 2014, 36(11): 2666-2671. doi: 10.3724/SP.J.1146.2013.01925.

YAN Junkun, LIU Hongliang, and DAI Fengzhou. Joint detection and tracking processing algorithm with constant false alarm rate property[J].&, 2014, 36(11): 2666-2671. doi: 10.3724/SP.J.1146.2013.01925.

赵兴刚： 男，1988年生，博士生，研究方向为雷达目标检测.

王首勇： 男，1956年生，教授，博士生导师，主要研究方向为信息与通信处理.

Foundation Items: The National Natural Science Foundation of China (61179014), Youth Science Fund Project (61302193)

An Improved Matrix CFAR Detection Method Base on KL Divergence

ZHAO Xinggang WANG Shouyong

(Air Force Early Warning Academy, Wuhan 430019, China)

The matrix CFAR detector is proposed according to information geometry theory, but its constant false alarm property is not analysed, and the matrix CFAR’s detection performance still needs to be improved. Firstly, the matrix CFAR’s constant false alarm property is analysed according to the normal law on matrix manifold, on this basis an improved matrix CFAR detector is proposed with replacing the geodesic distance with KULLBACK-LEIBLER Divergence (KLD). Finally, simulation experiments verify that the improved method has better detection performance.

Information geometry; Constant False Alarm Rate (CFAR) detection; Statistic manifold; Geodesic distance; KULLBACK-LEIBLER Divergence (KLD) (relative entropy)

TN957.51

A

1009-5896(2016)04-0934-07

10.11999/JEIT150711

2015-06-10；改回日期：2015-12-18；网络出版：2016-02-03

赵兴刚 565484636@qq.com

国家自然科学基金(61179014)，青年科学基金项目(61302193)