非均匀间隔OFD-LFM的MIMO雷达波形设计

李 慧 赵永波 冯大政 程增飞



非均匀间隔OFD-LFM的MIMO雷达波形设计

李 慧*赵永波 冯大政 程增飞

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

正交频分线性调频(OFD-LFM)信号是多输入多输出(MIMO)雷达的一种常用发射波形，在分析其空时特性的基础上，针对空域合成信号自相关旁瓣存在的问题，该文提出一种非均匀间隔的OFD-LFM波形，并给出了相应的波形设计方法。该方法建立空时联合优化的模型，采用序列二次规划求解得到各信号的频率间隔和初相。所设计波形的发射方向图近似全向，空域合成信号具有良好的相关性能。

MIMO雷达；波形设计；正交频分线性调频；序列二次规划

1 引言

多输入多输出(Multiple Input Multiple Output, MIMO)雷达的发射天线同时发射不同的信号，在接收端亦采用多个天线同时接收回波信号。对于集中式MIMO雷达[1]，其阵元间距较小，具有波形分集的优势，与传统相控阵雷达相比能够获得较高的角度分辨率和参数辨别能力。为了抑制干扰并增强不同目标回波信号的独立性，MIMO雷达一般采用相互正交的发射波形，即要求发射信号具有较低的互相关及自相关旁瓣。基于这一准则，文献[2-7]采用模拟退火、遗传算法、循环算法、约束非线性规划等设计了不同编码方式的正交波形。这些方法需要的迭代次数较多而造成了较大的运算量，而且当存在多普勒频移时性能会有较大的下降。针对这些问题，文献[8,9]设计了多普勒容忍性有所改善的正交相位编码波形，文献[10]提出了一种运算量较小的快速波形设计方法，文献[11,12]则采用空时编码提高了信号的相关性能。这些方法设计的波形性能有所改善，但是由于信号不可能理想正交，所以在对接收数据进行处理时不能实现信号的完全分离。而且这些信号都属于编码类波形，具有对多普勒频率比较敏感的固有缺陷，不利于对运动目标的检测。

线性调频信号能够解决雷达作用距离与分辨力的矛盾，同时具有对多普勒频率不敏感的优点，所以线性调频信号被应用于很多MIMO雷达发射波形中，并有很多学者提出了相应的波形设计方法。一类是将线性调频信号引入到离散频率编码波形，并通过优化设计得到相关性能良好的发射波形，但是这种波形仍然存在多普勒容忍性受限的问题。另一类就是正交频分线性调频(Orthogonal Frequency Division-Linear Frequency Modulation, OFD-LFM)信号。文献[17]对OFD- LFM信号的互相关函数进行了详细的分析，给出了最小化信号间互相关影响的参数之间的关系，指出了当频谱不重叠时发射信号间的互相关较小，但是其自相关受线性调频信号的限制旁瓣较高。文献[18]则从另一种信号处理方式(先进行接收波束形成再进行时空匹配滤波)出发，指出了频谱重叠OFD- LFM的时空匹配滤波结果(也就是空域合成信号的自相关)存在离散旁瓣，并因此设计了频谱重叠的OFD-LFM波形，但是其空域合成信号的自相关旁瓣仍然存在近区旁瓣高远区旁瓣低的缺陷。

针对该问题，本文对频谱重叠OFD-LFM空域合成信号的自相关旁瓣特性进行了分析，进而提出一种非均匀间隔的OFD-LFM波形，并基于文献[18]的信号处理方式给出一种相应的波形设计方法。所设计波形的发射方向图近似全向，空域合成信号相关性能较好，而且具有较强的多普勒容忍性，这些都能够在实际应用中提高MIMO雷达的目标检测性能。

2 OFD-LFM信号模型及空时特性

在MIMO雷达中，正交频分信号类似于步进频信号，各通道发射不同载频的信号，每个信号占用不同的频带，通过接收匹配处理和波束形成可以得到宽带效果，获得高分辨力。正如文献[17]所指出的，正交信号也可以设计为OFD-LFM信号，即每个发射信号内部采用线性调频信号，各发射通道信号占用不同的频带或频带有所重叠[18]。设MIMO雷达有个发射通道，其中第个通道发射的线性调频信号为，则有

为了得到良好的目标检测性能，文献[17]对MIMO雷达的OFD-LFM信号进行了设计，并对其正交性进行了分析，给出了最小化信号间互相关的参数设计，验证了当频谱不重叠时互相关最小，但是没有考虑空域合成信号的相关特性。从式(4)可以看出，在频谱不重叠时，影响空域合成信号自相关函数特性的主要是第1项，此时的分辨率低，且各权系数在,相同，使同相相加造成离散旁瓣；这些离散旁瓣很容易被检测到而成为假目标，造成虚警。针对该问题，文献[18]提出了频谱重叠的OFD-LFM波形，消除了离散旁瓣，但是其空域合成信号的自相关存在近区旁瓣较高的问题。

针对这两种波形的空域合成信号自相关旁瓣存在的问题，本文在对频谱重叠OFD-LFM波形的旁瓣特性进行分析的基础上，提出一种非均匀间隔的OFD-LFM波形，并针对其存在的缺陷给出一种非均匀间隔OFD-LFM的波形设计方法，该方法在方向图逼近全向的前提下，基于抑制空域合成信号的自相关旁瓣电平来进行OFD-LFM的信号设计。

3 非均匀间隔OFD-LFM的波形设计方法

上一节给出了OFD-LFM信号的空时特性，其中发射方向图反映着OFD-LFM信号的空域特性，决定着目标方向处电磁能量的大小；空域合成信号的自相关函数反映着OFD-LFM空域合成信号的时域特性，决定着脉冲压缩性能的好坏。现有方法都是在方向图全向(即信号完全正交)的条件下进行OFD-LFM信号设计的，也就是各信号间的频率间隔相等且为的整数倍，这样的要求就会造成空域合成信号的一些固有时域特性。

要解决OFD-LFM空域合成信号自相关旁瓣的问题，首先需要找出其旁瓣的固有特性。事实上，频谱重叠时影响旁瓣的主要是式(4)中后面的旁瓣项，假设造成左边旁瓣的某一项为

图2(a)为非均匀间隔OFD-LFM空域合成信号的最大自相关，即自相关峰值旁瓣电平(Auto- correlation Peak Sidelobe Level, APSL)最大。其中,，频率间隔为个互不相同且和为240 kHz的随机数，初相也是随机产生的。从图2(a)可以看出，非均匀间隔OFD-LFM空域合成信号的自相关不存在离散旁瓣，也不存在明显较高的近区旁瓣，能够有效避免虚警。但是其旁瓣依然较高，而且由于频率间隔各不相同，空域合成信号的自相关旁瓣不再具有固有特性，不同方位

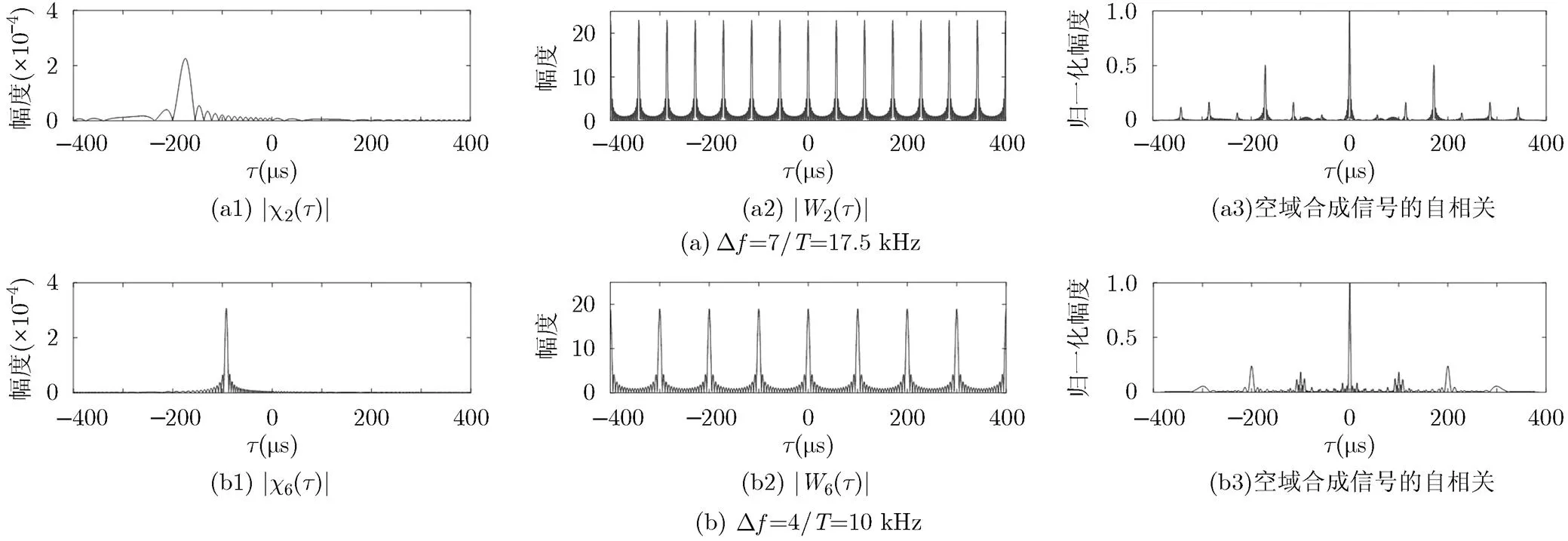
图 1 频谱重叠OFD-LFM的旁瓣特性

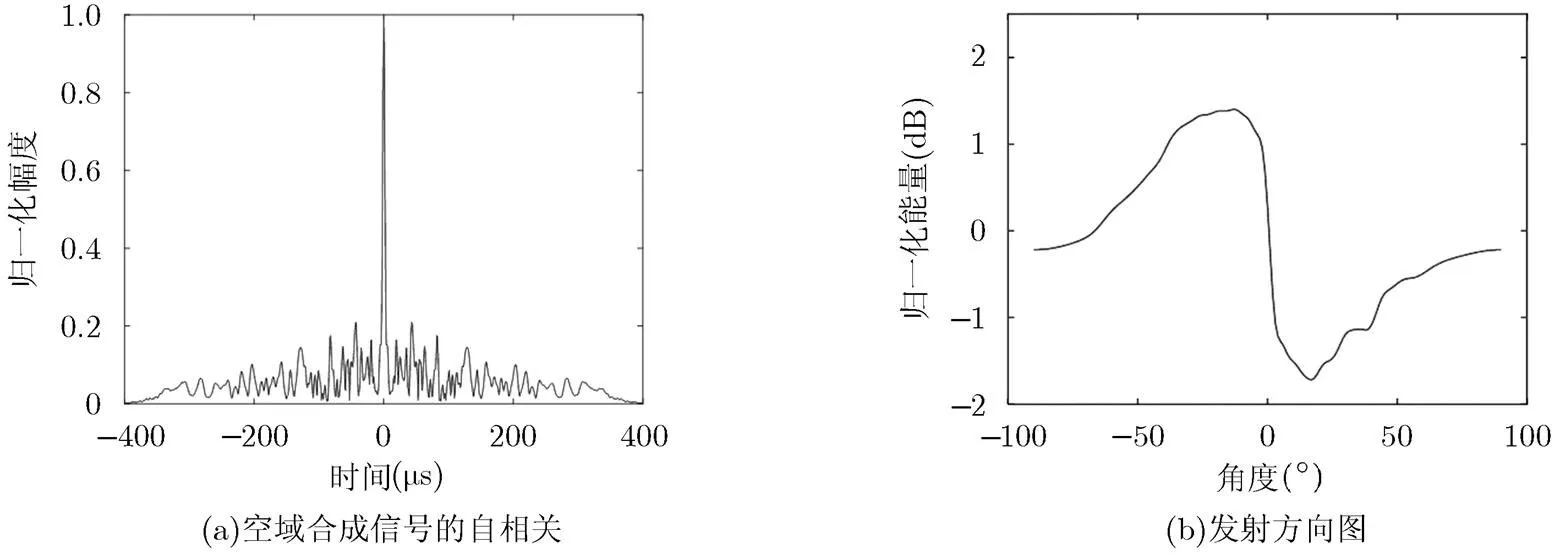
图 2 非均匀间隔OFD-LFM的空时特性

空域合成信号的自相关旁瓣就会有所不同，甚至变化较大。

图2(b)为非均匀间隔OFD-LFM的发射方向图，从图中可以看出，非均匀间隔OFD-LFM的发射方向图是高低起伏的。这是因为非均匀间隔OFD- LFM各发射信号的频率间隔各不相同且不再是的整数倍，所以各信号不能完全正交，导致发射能量不能在各方向等同分布，使发射方向图有较大的波动。

针对本文提出非均匀间隔OFD-LFM的相关特性及方向图存在的问题，我们给出一种非均匀间隔OFD-LFM的波形设计方法，该方法通过优化设计OFD-LFM的频率间隔和初相，得到空时特性良好的线性调频发射波形。为了使非均匀间隔OFD- LFM空域合成信号的自相关旁瓣在各方向都比较低，我们选择空域合成信号的最大APSL作为目标函数；同时，由式(3)可以看出，发射方向图主要取决于相关矩阵，为了使发射方向图接近全向，我们让信号的相关矩阵逼近单位阵。这样就可以对非均匀间隔OFD-LFM的波形设计建立式(7)所示的优化模型：

式(7)是一种对空时特性进行联合优化的模型，优化的目的是既要降低空域合成信号的自相关旁瓣，从而提高其脉压性能；又让发射方向图逼近全向，信号近似正交。因为该正交OFD-LFM波形设计方法是基于先接收波束形成后时空匹配滤波的信号处理结构，所以在目标函数中不考虑空域合成信号的互相关函数。需要指出的是，式(7)的目标函数是非凸的，很难求得最优解，而且具有非线性约束，因此采用序列二次规划[7](Sequential Quadratic Programming, SQP)法求解。值得考虑的一个问题是，初始点的选取会影响解的质量，由于没有准确的先验信息，我们选取和为的一组随机数作为的初始值，而的初始值在范围内随机产生。

4 仿真分析

图3(a)所示为OFD-LFM空域合成信号的最大自相关。从图中可以看出，文献[17]的波形存在离散旁瓣；文献[18]的波形没有离散旁瓣，但是近区旁瓣较高；而用本文方法设计的非均匀间隔OFD-LFM信号既不存在离散旁瓣，也没有较高的近区旁瓣，而且所有方向空域合成信号的自相关旁瓣都得到了有效抑制。总体上说，本文方法所设计的非均匀间隔OFD-LFM波形其空域合成信号的自相关旁瓣较低，分布比较均匀且平坦，具有较好的脉冲压缩性能，既避免了虚警问题，也不会影响弱目标的检测，使MIMO雷达的目标检测性能有所提高。

图3(b)所示为各波形的发射方向图，从图中可以看到，文献[17]和文献[18]的波形由于频率间隔相等且是的整数倍，信号完全正交，发射方向图为理想全向；本文方法设计的非均匀间隔OFD- LFM波形，频率间隔不相等且不能保证是1/的整数倍，能量分布无法实现理想全向，但是，因为在优化过程中让信号的相关矩阵逼近了单位阵，所以其发射方向图是近似全向的，同时也证明了该约束的有效性。

表1给出了不同调频带宽下本文方法所设计波形空域合成信号的自相关性能。从表中可以看出，用本文方法设计调频带宽不同的波形，其空域合成信号的自相关性能是略有不同的。当调频带宽特别大或特别小时，最大APSL较高；当调频带宽比较适中时，最大APSL都在-20 dB左右。为了进一步对比，表1同时给出了相同调频带宽下均匀间隔OFD-LFM的结果。通过比较可以看出，相同调频带宽下，本文方法所设计的非均匀间隔OFD-LFM空域合成信号的最大APSL都低于均匀间隔OFD- LFM，具有较好的脉冲压缩性能。

除空域合成信号的自相关外，空域合成信号的互相关同样重要。图4 给出了文献[17]、文献[18]及本文方法所设计OFD-LFM波形与空域合成信号的互相关。从图中可以看出，由于信号间频率间隔的限制，文献[17]、文献[18]空域合成信号的互相关与其自相关旁瓣类似，文献[17]具有离散旁瓣，而文献[18]在某区域具有较集中的高旁瓣。本文方法的互相关则较小且分布相对平坦。

由于OFD-LFM信号的多普勒容忍性是与信号间的频率间隔有关的，所以将本文方法的多普勒容忍性与相同调频带宽下的等间隔波形进行对比，比较结果如图5所示，其中信号的调频带宽为140 kHz。从图中可以看出，本文方法空域合成信号的多普勒容忍性比等间隔波形要差一些，特别是在

图3 OFD-LFM的时域相关特性和方向图

表 1 不同调频带宽下所设计OFD-LFM波形的性能

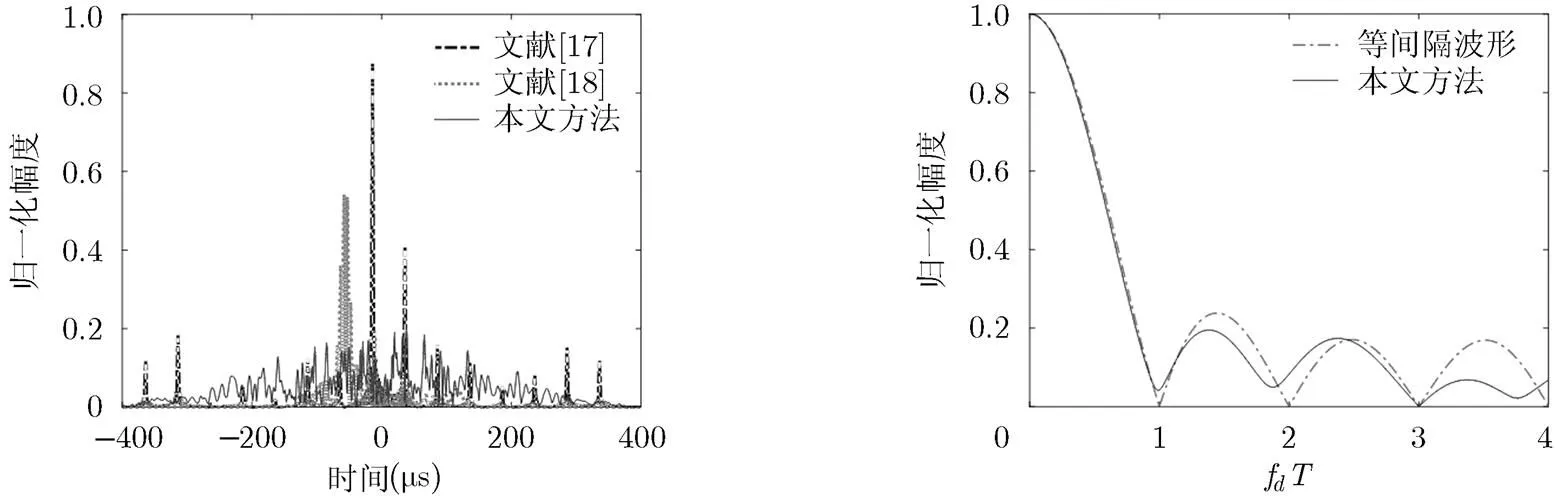
图4 空域合成信号的互相关 图5 空域合成信号的多普勒容忍性

时，这是因为本文方法所设计波形各信号间的频率间隔不相等，空域合成信号的多普勒容忍性也就失去了固有特性。

5 结论

针对OFD-LFM空域合成信号的自相关旁瓣存在的问题，本文对其旁瓣固有特性进行了分析，进而提出一种非均匀间隔OFD-LFM的MIMO雷达发射波形，并给出一种相应的波形设计方法，通过求解统一的数学模型得到各线性调频信号的频率间隔及初相。所设计的波形不仅发射方向图接近全向，而且空域合成信号的自相关旁瓣得到了有效抑制。

[1] LI J and STOICA P. MIMO radar with colocated antennas [J]., 2007, 24(5): 106-114. doi: 10.1109/MSP.2007.904812.

[2] DENG H. Polyphase code design for the orthogonal netted radar systems[J]., 2004, 52(11): 3126-3135. doi: 10.1109/TSP.2004.836530.

[3] LIU B, HE Z S, and HE Q. Optimization of orthogonal discrete frequency-coding waveform based on modified genetic algorithm for MIMO radar[C]. Proceedings of the International Conference on Communication, Circuits and Systems, Kokura, 2007: 966-970. doi: 10.1109/ICCCAS.2007. 4348208.

[4] MEHANY W, JIAO L C, and HUSSIEN K. Orthogonal discrete frequency-coding waveform design based on modified genetic algorithm for MIMO-SAR[C]. Proceedings of IEEE 9th Conference on Industrial Electronics and Applications (ICIEA), Hangzhou, 2014: 1082-1086. doi: 10.1109/ICIEA. 2014.6931325.

[5] HE H, STOICA P, and LI J. Designing unimodular sequence sets with good correlations—including an application to MIMO radar[J]., 2009, 57(11): 4391-4405. doi: 10.1109/TSP.2009.2025108.

[6] BABUR G, KRASNOV O A, YAROVOY A,. Nearly orthogonal waveforms for MIMO FMCW radar[J]., 2013, 49(3): 1426-1437. doi: 10.1109/TAES.2013.6557996.

[7] 胡亮兵, 刘宏伟, 吴顺君. 基于约束非线性规划的MIMO雷达正交波形设计[J]. 系统工程与电子技术, 2011, 33(1): 64-68. doi: 10.3969/j.issn.1001-506X.2011.01.13.

HU L B, LIU H W, and WU S J. Orthogonal waveform design for MIMO radar via constrained nonlinear programming[J]., 2011, 33(1): 64-68. doi: 10.3969/j.issn.1001-506X.2011.01.13.

[8] YANG J, QIU Z K, JIANG W D,. Poly-phase codes optimization for multi-input multi-output radars[J]., 2013, 7(2): 93-100. doi: 10.1049/iet-spr. 2012.0195.

[9] YANG J, WANG H Q, JIANG W D,. Complementary- based chaotic phase-coded waveforms design for MIMO radar[J].,&, 2013, 7(4): 371-382. doi: 10.1049/iet-rsn.2012.0123.

[10] 赵宜楠, 张涛, 李风从, 等. 基于交替投影的MIMO 雷达最优波形设计[J]. 电子与信息学报, 2014, 36(6): 1368-1373. doi: 10.3724/SP.J.1146.2013.01198.

ZHAO Y N, ZHANG T, LI F C,. Optimal waveform design for MIMO radar via alternating projection[J].&, 2014, 36(6): 1368-1373. doi: 10.3724/SP.J.1146.2013.01198.

[11] 杜晓林, 苏涛, 王旭, 等. 基于Golay互补序列空时编码的MIMO雷达波形设计[J]. 电子与信息学报, 2014, 36(8): 1966-1971. doi: 10.3724/SP.J.1146.2013.01524.

DU X L, SU T, WANG X,. Golay complementary sequence with space time coding for MIMO radar waveform design[J].&, 2014, 36(8): 1966-1971. doi: 10.3724/SP.J.1146.2013.01524.

[12] ZHOU S H, LIU H W, WANG X,. MIMO radar range- angular-doppler sidelobe suppression using random space- time coding[J]., 2014, 50(3): 2047-2060. doi: 10.1109/ TAES.2013.120681.

[13] LIU B. Orthogonal discrete frequency-coding waveform set design with minimized autocorrelation sidelobes[J]., 2009, 45(4): 1650-1657. doi: 10.1109/TAES.2009.5310326.

[14] GAO C C, TEH K C, and LIU A F. Orthogonal frequency diversity waveform with range-doppler optimization for MIMO radar[J]., 2014, 21(10): 1201-1205. doi: 10.1109/LSP.2014.2329944.

[15] WANG W Q, SO H C, HUANG L T,. Low peak-to- average ratio OFDM chirp waveform diversity design[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, 2014: 8351-8354. doi: 10.1109/ICASSP.2014.6855230.

[16] WANG W Q. Large time-bandwidth product MIMO radar waveform design based on chirp rate diversity[J]., 2015, 15(2): 1027-1034. doi: 10.1109/JSEN. 2014.2360125.

[17] 刘波, 韩春林, 苗江宏. MIMO雷达正交LFM信号设计及性能分析[J]. 电子科技大学学报, 2009, 38(1): 28-31.

LIU B, HAN C L, and MIAO J H. OFD-LFM signal design and performance analysis for MIMO radar[J]., 2009, 38(1): 28-31.

[18] 赵永波, 水鹏朗, 刘宏伟, 等. 基于线性调频信号的综合脉冲与孔径雷达波形设计方法[J]. 电子学报, 2010, 38(9): 2076-2082.

ZHAO Y B, SHUI P L, LIU H W,. Waveform design for synthetic impulse and aperture radar based on LFM signals [J]., 2010, 38(9): 2076-2082.

李 慧： 女，1990年生，博士生，研究方向为MIMO雷达发射波形设计.

赵永波： 男，1972年生，教授，博士生导师，研究方向为阵列信号处理、MIMO雷达波形设计及波达方向估计等.

冯大政： 男，1959年生，教授，博士生导师，研究方向为雷达信号处理、信号参数估计、仿大脑信息处理、场景感知、模式识别等.

MIMO Radar Waveform Design for OFD-LFM with Various Frequency Steps

LI Hui ZHAO Yongbo FENG Dazheng CHENG Zengfei

(National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

Orthogonal Frequency Division-Linear Frequency Modulation (OFD-LFM) signal is widely used in Multiple Input Multiple Output (MIMO) radar systems. For solving the problems of the auto-correlation sidelobes of the spatial synthesized signals, an analysis is made of the inherent sidelobe property. Furthermore, OFD-LFM with various frequency steps is proposed and the waveform design method is given. The optimization model is established based on the temporal property and spatial property jointly. Then, the frequency steps and initial phases are optimized by Sequential Quadratic Programming (SQP). The transmitted power of the designed waveform is approximately equal in all directions, and the spatial synthesized signals have good correlation properties.

MIMO radar; Waveform design; Orthogonal Frequency Division-Linear Frequency Modulation (OFD- LFM); Sequential Quadratic Programming (SQP)

TN958

A

1009-5896(2016)04-0927-07

10.11999/JEIT150814

2015-07-08；改回日期：2015-12-31；网络出版：2016-02-26

李慧 lihui1990happy@126.com