扩频通信中FFT捕获算法的改进
陶 峰,王静温,田梦雪
扩频通信中FFT捕获算法的改进
陶 峰1,王静温2,田梦雪2
(1.西安卫星测控中心宇航动力学国家重点实验室,陕西西安710043;2.北京遥测技术研究所,北京100076)
针对现有捕获算法中存在累积次数多、捕获时间长和捕获精度不高的问题,对传统的FFT算法进行了部分改进,即利用数据分块、补零和伪码相位的圆周移位增加了相干积分时间进而减少了非相干累积次数,并将二维捕获转化为一维捕获。在相同捕获精度下提高了捕获速度。仿真结果表明,该算法对载噪比低至30 dB的扩频信号仍能满足捕获要求。
扩频通信;扩频捕获;FFT算法;数据分块
引用格式:陶 峰,王静温,田梦雪.扩频通信中FFT捕获算法的改进[J].无线电工程,2016,46(5):41-44.
0 引言
目前,扩频信号捕获方法按相关运算实现方式的不同主要分为4种:滑动相关器算法、匹配滤波器算法、时域并行FFT算法和频域并行FFT算法[1]。由于高效的FFT处理技术可实现伪码相位或载波频率任意一维的并行搜索过程,减少了捕获时间,因此,基于FFT的捕获算法[2]成为目前工程应用的设计主流。但传统的FFT捕获算法在低信噪比时(载噪比<37 dBHz)需要较大的非相干累积次数,捕获时间无法满足任务需求[3]。
针对该问题,本文对传统的FFT算法进行了部分改进,利用双块补零(Double Block Zero Padding,DBZP)伪码圆周移位减少了非相干累积次数,并将二维捕获转化为一维捕获,提高了捕获速度[4]。本文详细分析了改进算法的原理和性能,并利用Matlab完成仿真验证,仿真结果表明在载噪比C/N0=30 dBHz、多普勒为50 kHz时,该算法可正确捕获到伪码相位。
1 算法原理
1.1 传统FFT捕获原理
FFT捕获算法是利用时域卷积等于频域相乘原理实现伪码相位的并行捕获,高效的FFT处理技术可实现伪码相位或载波频率任意一维的并行搜索过程,减少了捕获时间[5],其原理框图如图1所示。
在扩频接收机中,假设接收信号为s(n),本地伪码为p(n),捕获运算采用的是相关运算[6]。接收信号与本地信号的相关函数可表示为:
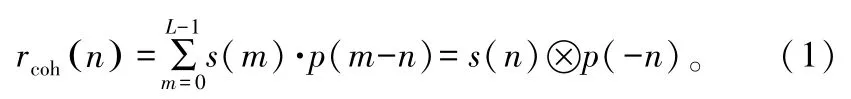
式中,L为伪码序列的周期长度;⊗表示卷积运算。由于时域卷积等于频域相乘,因此,

式中,S(K)为输入信号s(n)经过FFT变换后的频域表示;P*(K)为本地伪码序列经过FFT变换后频域的共轭[7],通过搜索逆FFT之后的幅度最大值即可得到接收信号的伪码相位值[8]该算法在较高信噪比时,捕获时间及捕获概率均能满足任务需求。但当信号信噪比较低时,需要长时间的累积增加相关能量,捕获时间随之变长,无法满足任务需求[9]。
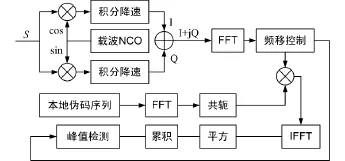
图1 传统FFT捕获原理
1.2 改进的FFT捕获算法
改进的FFT的捕获算法是在传统的FFT捕获上增加了 DBZP模块和圆周移位模块[10],如图2所示。
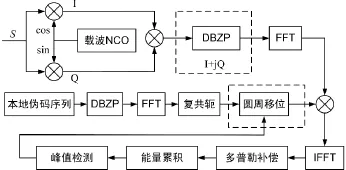
图2 改进的FFT捕获算法
DBZP模块是将长点数的相关计算转化为多段短点数FFT计算,降低FFT运算时间。圆周移位模块替换了在不同载波多普勒搜索单元下对输入信号的重复载波剥离和FFT运算,实现在多普勒搜索单元和码相位的二维搜索过程中,只需对输入信号进行一次FFT操作,减少捕获算法执行过程中的FFT运算次数[11],从而达到节省捕获时间的目的。
算法原理如下:先将接收到扩频信号变为基带信号,取一段长为Ns×Sblock的数据进行分块,其中Ns为分块数,Sblock为每块数据中采样点数。将相邻2块组合成2Sblock采样点的数据块,对其做2Ns点离散傅里叶变换[12]:
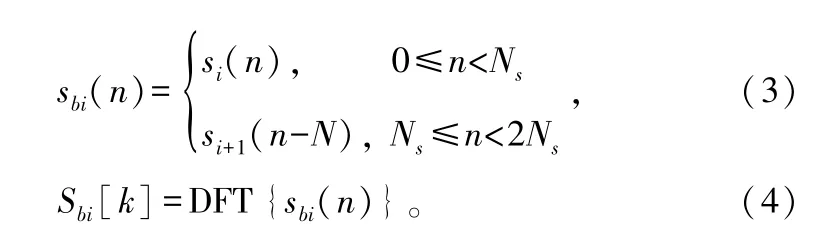
式中,si(n)为第i个数据子块;sbi(n)为组合后第i个数据块;Sbi[k]为组合块的离散傅里叶变换。同样将本地伪码序列分为Nb块,每块含Sblock个采样点。将每个伪码子块后补Sblock点零拓展成2Sblock采样点的伪码块,求其离散傅里叶变换:
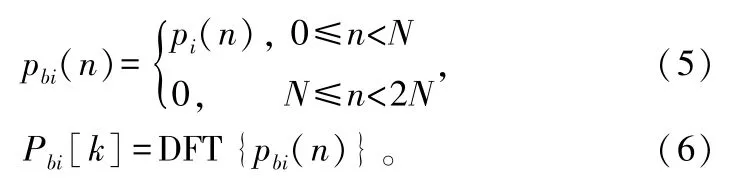
当伪码块相对于数据块进行循环移位时,利用式(1)和式(2)求得2块数据的相关值。通过伪码圆周移位获得全部伪码相位上相关值能量[13]。对相关值做码多普勒补偿后,对相关峰能量进行累加。在捕获过程中只要有相关峰值能量大于门限值,则认为捕获成功[14]。
2 捕获性能分析
2.1 计算量分析
以码率为2 000 bps,伪码速率为5.115 Mcps,多普勒捕获范围为-80~80 kHz为例,在多普勒分辨率为5 kHz,伪码相位分辨率为1/2码chip的条件下,传统FFT捕获算法和改进的FFT捕获算法计算量如表1所示。
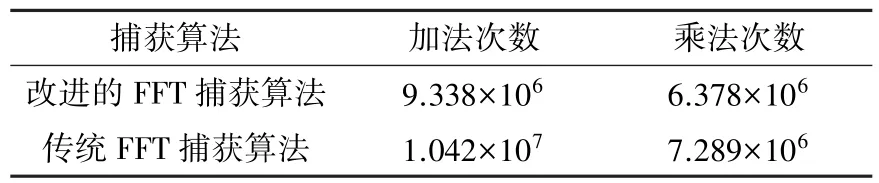
表1 计算量对比表
表1中,1次复数乘法运算相当于4次实数乘运算和2次实数加运算,1次复数加相当于2次实数加法运算,加法、乘法和FFT变换操作对应的操作数均换算成实数。
2.2 累加次数和时间分析
在2.1小节的信号条件下,可以计算捕获概率为95%以上时,传统FFT算法和改进的FFT算法的所需的非相干累计次数N和所需的累积时间T(s),计算结果如表2所示。
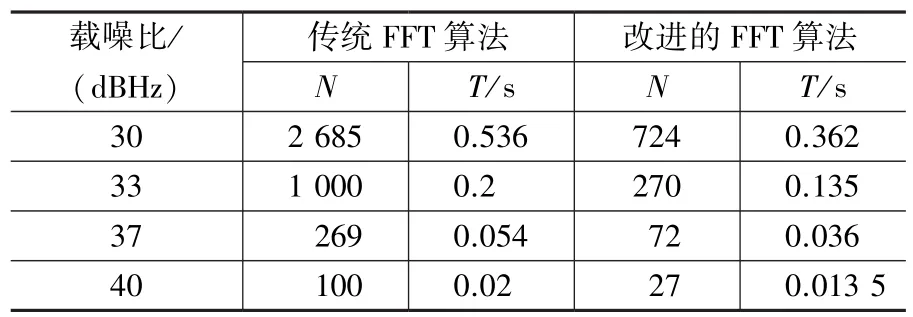
表2 传统FFT算法与改进的FFT算法非相干累计次数对比
由表2可以看出,当信噪比较低时,改进的FFT捕获算法的非相干累计次数明显小于传统的FFT算法,这就大大减少了能量累积的运算量,提高了捕获速度。
3 仿真验证
为验证改进的FFT捕获算法在低信噪比下的性能,利用Matlab搭建了仿真模型,模拟了低信噪比模拟源,其仿真参数为:伪码码率为5.115 Mcps,数据码率为5 000 bps,多普勒偏移为50 kHz,伪码相位偏移457 chip(即5 000采样点)。传统FFT捕获算法相干积分长度为2个伪码周期,改进的FFT捕获算法的相干积分长度为2个数据码片。当C/N0=33 dBHz时,传统 FFT捕获算法和改进的FFT捕获算法的仿真结果如图3和图4所示。当C/N0=30 dBHz时仿真结果如图5和图6所示。
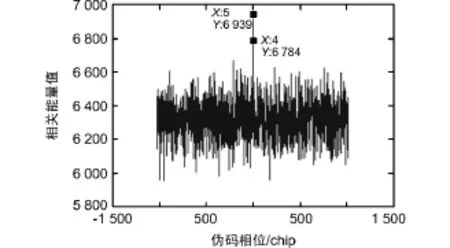
图3 传统FFT捕获算法结果
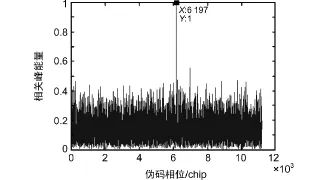
图4 改进的FFT捕获算法结果
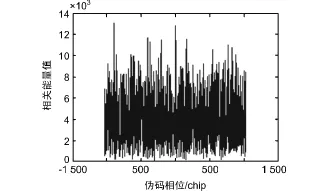
图5 传统FFT捕获算法结果

图6 改进的FFT捕获算法结果
从图3和图4可以看出,当载噪比为33 dBHz时,改进的FFT算法的相关峰值明显高于传统FFT捕获算法。由图5和图6可知,当载噪比为30 dBHz时,传统FFT捕获算法中相关峰淹没在噪声中,无法正确捕获信号。而改进的FFT算法可得到明显的相关峰,捕获的伪码相位在11 200个采样点中第6 197个采样点,与预置值偏离3个采样点,在允许误差范围内。
4 结束语
本文比较分析了现有的二维搜索扩频捕获算法,针对这些算法在实现过程中存在非相干累计次数较多、捕获时间长的问题,对传统的FFT算法进行了改进。该算法利用数据分块、数据补零和伪码圆周移位,减少了非相干累积次数并将二维捕获过程转换为一维捕获,在相同捕获概率下,降低了捕获时间,提高了捕获精度。在理论分析的基础上,通过仿真验证了该算法在低信噪比(30 dBHz)下的捕获性能,为后续工程应用提供了参考。
[1] 黎 山.GPS软件接收机基带关键技术的研究与实现[D].南京:东南大学,2012.
[2] 赵鹤群,杨家成.直接序列扩频通信中的FFT快速捕获方法[J].舰船电子工程,2015(5):72-74.
[3] 张 凯.高动态扩频信号快速捕获算法研究[D].西安:西安电子科技大学,2014.
[4] 焦瑞祥,茅旭初.基于DBZP方法的微弱GPS信号的快速捕获[J].电子学报,2008,36(12):2 285-2 289.
[5] 莫建文.弱信号环境下高性能GPS接收机关键技术研究[D].西安:西安电子科技大学,2011.
[6] 秦率刚,王 星,程嗣怡,等.扩频通信系统中一种FFT算法的快速捕获方法[J].现代防御技术,2012,40 (2):150-154.
[7] VAN NEE D J R,COENEN A J R M.New Fast GPS Code-Acquisition Technique Using FFT[J].Electronics Letters,1991,27(2):158-160.
[8] SASCHA M,SPANGENBERG,IAIN SCOTT.An FFTBased Approach for Fast Acquisition in Spread Spectrum Communication Systems[J].wireless Personal Communications,2000,39:27-56.
[9] LIN D M,TSUI J B Y,HOWELL D.Direct P(Y)-Code Acquisition Algorithm for a Software GPS Receiver[C]∥Proc.ION GPS.UT,1999:363-367.
[10]LIN D M,TSUI J B Y.Comparison of Acquisition Methods for Software GPS Receiver[C]∥Proc.ION GPS.Salt Lake City:UT,2000:2 385-2 390.
[11]TSUI J B Y.Fundamentals of Global Positioning System Receivers:A software Approach(Second Edition)[M]. New York:Wiley-Interscience,2004.
[12]张少波,毕光国.直接序列扩频系统中的捕获[J].电讯技术,1995(4):28-32.
[13]赵 琳,高帅和,丁臻成.基于FFT的高动态GPS信号捕获方法优化[J].系统工程与电子技术,2011,33(1):151-156.
[14]ZIEDAN N I.GNSS Receivers for Weak Signals[M].Norwood:Artech House,2006.
Improvement of FFT Acquisition Algorithm in Spread Spectrum Communication System
TAO Feng1,WANG Jing-wen2,TIAN Meng-xue2
(1.State Key Laboratory of Aerospace Dynamics,China Xi’an Satellite Control Center,Xi’an Shaanxi 710043,China;2.Beijing Research Institute of Telemetry,Beijing 100076,China)
In order to solve the problems in current acquisition algorithms such as long accumulation length,long acquisition time and low resolution,the classical FFT acquisition algorithm is partly improved.By using the data block,zero-padding and PN code cycleshift,the coherent integration time increases,the non-coherent accumulation times decrease and the two-dimensional acquisition process is converted into one-dimensional acquisition.In the same,the acquisition is accelerated with the same acquisition accuracy.The simulation results show that the proposed algorithm can meet the requirement of acquisition for the spread spectrum signal with carrier to noise ratio down to 30 dB.
spread spectrum communication;spread spectrum acquisition;FFT algorithm;data block
TN911.7
A
1003-3106(2016)05-0041-04
10.3969/j.issn.1003-3106.2016.05.11
2016-01-28
陶 峰 男,(1966—),高级工程师。主要研究方向:无线电测量技术及航天测控站总体设计。
王静温 女,(1987—),工程师。主要研究方向:深空测控通信技术。

