风光联合优化配置的多目标机会约束规划方法
夏 澍,顾劲岳,葛晓琳,钱耀兴
风光联合优化配置的多目标机会约束规划方法
夏 澍1,顾劲岳1,葛晓琳2,钱耀兴1
(1.国网上海市电力公司市北供电公司,上海 200072;2.上海电力学院电气工程学院,上海 200090)
针对风速、太阳辐射、负荷的随机性和相关性,综合考虑成本、网损和电压质量,应用蒙特卡洛模拟法和机会约束规划法建立了风力发电机组和光伏方阵两种分布式可再生能源接入现有配电网的多目标优化配置模型。在蒙特卡洛法的基础上,提出了多区间划分、建立概率分布的方法,从而减少抽样次数。在求解模型过程中,首先利用多目标微分进化算法进行全局寻优,得到一组pareto最优解集,然后采用基于熵的模糊多属性决策方法选取折衷最优解。IEEE-33节点配电系统规划结果验证了模型的合理性和方法的有效性。
风力发电机组;光伏方阵;优化配置;蒙特卡洛法;机会约束;多目标优化
0 引言
分布式电源(Distributed Generation, DG)接入配电网,会对配电网运行带来影响,具体影响程度与DG的接入点和接入容量有关[1-2],因此DG的优化配置问题得到了广泛的关注。文献[3]以网损最小为目标,利用进化规划算法确定DG的接入点和接入容量。文献[4]在计及DG发电成本的同时兼顾减排指标,提出了主动配电网低碳优化模型。文献[5]综合考虑网损、电压质量和电流质量,并运用加权法和遗传算法确定DG的配置方案。上述模型只针对柴油机组、微型燃气轮机组等出力灵活可控的DG,而没有考虑到风力发电机组(Wind Generations, WG)、光伏方阵(Photovoltaic, PV)等具有不确定性的分布式可再生能源(Distributed Renewable Resources, DRR)。文献[6]针对风速的随机性,以年综合费用最小为目标,建立了机会约束规划模型,并采用概率潮流和混合蛙跳算法对模型进行了仿真,为不确定性可再生能源规划问题提供了一种求解思路。风速和太阳辐射在时间和地域上具有很强的互补性[7],因此WG和PV方阵联合优化配置可能会带来更好的效益。然而WTG和PV方阵都是不确定性电源,并且风速和太阳辐射之间具有一定的相关性,综合考虑WG和PV的优化配置问题求解起来更加困难,目前还很少见到这方面的研究。
本文针对风速、太阳辐射量、负荷的随机性和相关性,采用了更加精确的WG和PV发电模型,利用蒙特卡洛法模拟实际运行情况,并综合考虑了成本、网损和电压质量,建立了分布式可再生能源优化配置的多目标机会约束规划模型。蒙特卡洛法计算量大,因此本文在其基础上提出了多区间划分、建立概率分布的方法,减少了抽样次数。在求解DRR优化配置模型时,首先利用多目标微分进化算法获得一组均匀分布的Pareto最优解集,为最终决策提供了优良的候选方案,进而利用基于熵的模糊多属性决策方法协调各个目标,得到折衷最优解。最后对IEEE-33节点配电系统进行仿真计算,结果验证了模型的合理性和方法的有效性。
1 DRR的计算模型
1.1 WG
WG的输出功率通常与风速、风力机个数以及风电机组同时率有关,具体计算模型如式(1)[8]。

式中:W()为时刻风力发电机组的发电功率;w()为时刻风力机的发电功率,与风速密切相关,计算模型见文献[8];W为风力机个数;W为风电机组同时率系数(W≤1),可根据风电场实际地理位置确定。
1.2 PV
PV的输出功率不仅与当地的太阳辐射量和选取的光伏电池型号有关[9],还会受PV安装倾斜角的影响。对于固定式光伏方阵,很多学者都将倾角取为年发电量最大角[10],但这样做只适用于独立PV。对于与风力发电互补的PV,倾角的选取还与风力机发电量等因素有关。因此,为了更精确地表示光伏方阵的发电功率,本设计将倾斜角作为决策变量代入运算。PV发电功率计算公式如式(2)。
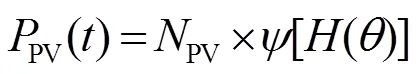
式中:PV()为时刻PV的发电功率;PV为光伏电池个数;为PV倾角;()表示倾斜面上太阳总辐射量;()表示单个光伏电池发电量,具体计算模型可以参考文献[10]。
1.3 随机变量模拟方法
通常风速概率密度函数可以用Weibull函数W()来表示,太阳辐射量概率密度可以用Beta函数PV()来表示,因此文献[11]根据解析法,利用W()PV()卷积运算表示风速和太阳辐射量在各种组合下的概率密度,但这种方法假设风速和太阳辐射量是独立的个体,没有考虑到两者之间的相关性。蒙特卡洛模拟法是在一个时间跨度上进行大量抽样仿真,能够更好地体现负荷、风速和太阳辐射量之间的联系,更准确地重现系统运行情况,但是算法计算量大,耗时较长。因此,本文在蒙特卡洛概率抽样的基础上,提出了多区间划分、建立概率分布关系的方法,具体计算流程如下:
1) 将全年负荷按月份划分为三个部分:夏季、冬季、春秋季;每天按照负荷大小划分为三部分:高峰、中间、低谷,则一共将1年划分为3×3个时间段,每个时间段是一个集合,记为l,=1, 2,…,,这里=9,每个时间段发生的概率是τ。
2) 根据水平面上的太阳总辐射量、水平面上的散射辐射量和光伏方阵倾角,计算出光伏方阵倾斜面上的太阳总辐射量,然后将倾斜面上的太阳总辐射量区间[0,max]划分为个区间,第个区间集合记为h,=1, 2, …,。
3) 将风速区间[ci,co]划分为若干个区间,同时将风速[0,ci]和[co, +∞]归为一个区间,这样就将风速分为了个区间,第个区间集合记为v,=1,2,…,。
4) 根据划分的区间,统计出负荷、太阳辐射和风速之间的概率关系如下:

(4)
式中:η表示负荷在l区间内、太阳总辐射量在h区间内、风速在v区间内的发生概率;为系统运行状态总个数,。通过上述方法,可以将比较相似的运行状态归类到一个区间,从而大大减少了抽样次数。
2 DRR优化配置的多目标机会约束规划模型
2.1 目标函数
对于风力机和光伏方阵的电源优化配置问题,从经济效益、节能效益及电能质量等多个角度出发,选取成本指标、网损指标和电压指标进行综合评价。同时考虑到风速和太阳辐射具有一定的随机性,以上三个指标也都包含随机变量,因此本文取它们的数学期望作为新的目标函数。
1) 成本指标
成本指标选用电源规划前后每年系统总成本的比值,其定义如式(5)。

式中:DGg为规划后在状态下的输电网供电功率;P为规划前在状态下的输电网供电功率;u表示在状态下的电网电价;u表示在状态下的电网电价;W、PV分别为风力发电机组和光伏方阵的投资、维护和运行费用,采用的是全寿命周期成本等年值的计算方法,具体模型参考文献[12]。
2) 网损指标
分布式可再生能源接入电网能够带来一个明显的节能效益就是降低网损,因此,网损评价指标是一项重要的技术指标,其定义如式(6)[5]。

式中:LDGg表示规划后在状态下的网损值;Ln表示规划前在状态下的网损值。
3) 电压指标
分布式可再生能源能够改善电压分布情况,因此电压指标定义如式(7)[5]。

式中:N为节点总数;V、0g分别表示在状态下节点和首节点的电压幅值;w为节点的权重因子,表示该节点的重要等级。
综合考虑成本、网损和电压这三个评价指标,分布式可再生能源规划问题的目标函数如下:

式中,为优化方案。在该模型中,存在三个目标,由于各个目标之间存在冲突,无法保证所有目标值同时达到最小,因此只能得到一组非劣解集(Pareto解集)。Pareto解集的特点是,在解集中,任一个体都至少存在一个目标优于其他所有个体。
2.2 约束条件
在分布式可再生能源规划问题中,约束条件包含随机变量,可采用机会约束规划模型,因此节点电压约束和支路电流约束都以概率的方式表示。
1) 潮流方程约束:
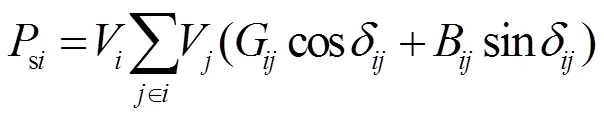
(10)
2) DRR最大安装节点数约束[3]:

3) DRR最大安装容量约束[3]:
(12)
4) 节点电压约束:

5) 支路电流约束:
(14)
式中:s、si分别为节点的有功和无功注入量;∈表示所有与节点直接相连的节点,包括=;G、B分别为节点导纳矩阵相应的实部和虚部;δ为支路两端节点的相角差;U表示是否在节点安装DRR,1代表安装,0代表不安装;为DRR安装最大节点数;Wi、PVi分别为第个节点安装的风力发电机组容量和光伏方阵容量;DRRmax为DRR最大允许安装容量;r{·}表示{·}中事件成立的概率;Vmax、Vmin分别为节点的最大允许电压值和最小允许电压值;L、Lmin和Lmax分别为支路的电流值、最小允许电流值和最大允许电流值;V、L为事先给定的置信水平。
3 模型求解
3.1 多目标微分进化算法
针对多目标优化问题,传统的方法就是利用权重、约束等措施,将多目标问题转换为单目标问题进行求解,具有很大的局限性。近年来,多目标优化算法因其不需要设置各个目标的权重,而是利用非劣排序的方法找到一组均匀分布的非劣pareto解集的特点已成为研究热点,其中典型的两个算法是SPEA2和NSGA-II。文献[13]在微分进化算法的基础上,引入了NSGA-II中的非劣排序措施,提出了多目标微分进化算法(Differential Evolution for Multiobjective Optimization, DEMO),该算法在多个测试问题上表现出的搜索性能优于NSGA-II。因此本文选用DEMO算法。
3.2 基于信息熵的模糊多属性决策方法
在实际优化配置过程中,最终实施的方案一般只有一个,因此决策者需要从Pareto最优解集中选取一个折衷最优解。本文利用基于信息熵的模糊法进行决策,其计算流程如下:
1) Pareto解集中每个决策单元的各个属性对应的满意度用模糊隶属函数来表示,定义如式(15)[14]。
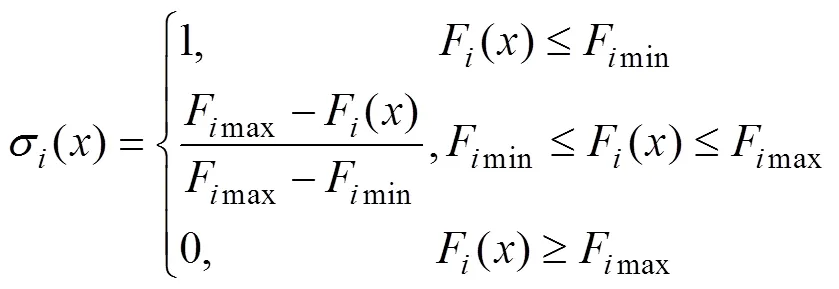
式中:σ()、F()分别表示决策单元的第个属性对应的满意度和数值,=1,2,…,obj;obj表示目标个数;Fmax和Fmin分别表示第个目标函数的最大值和最小值。
2) 利用信息熵确定各个属性的权重系数ω,=1,2,…,obj;并计算各个决策单元的模糊效用值(), 计算公式如下:

3) 根据()值,从大到小对Pareto解集进行排序和选优,()值最大的就是最优折衷解。
4 算例分析
本文以IEEE-33节点配电系统为例进行计算,线路参数见文献[15],负荷数据略有修改,全年尖峰时刻系统总负荷为4 086.5 kW和2 530 kvar,首节点电压为1.05 p.u.,节点电压取值范围为0.95~1.05 p.u.,各节点权重相等,线路电流传输上限为0.3 kA,电网固定电价为0.55元/kWh。风速数据和太阳辐射量数据以及风力发电机和光伏电池的参数详见文献[12],DRR待选安装节点编号为1~32,共32个,最大DRR安装节点数为两个,最大安装总容量为2 000 kW。DRR优化配置前,全年系统总成本为1 222.07万元,全年网损期望值为83.07 kW,全年电压偏差期望值为0.031 p.u.。
由于风速和太阳辐射量数据选用的周期是一年,如果用蒙特卡洛法按小时尺度来抽样,需要计算的样本数目为8 760个,计算量较大。而利用本文提出的区间划分法计算,当风速和太阳总辐射量区间数和都选为4时,需要计算的样本数目为144个,计算量大幅减小。而且当能够获取的风速和太阳辐射量数据周期更长时,如为3年,利用蒙特卡洛法需要计算的样本数目为26 280个,而所提的区间划分法需要计算的样本数据依然为144个,更能体现出本文所提方法的优越性。
多目标微分进化算法参数设置如下:种群规模为100,最大迭代次数为600,变异因子为0.5,交叉因子为0.4。置信水平V和L都为0.99,计算得到的patero解集分布情况如图1所示。从图1中可以看出3个目标间存在互斥的关系。在patero解集中选取以下四个解:成本指标最优、网损指标最优、电压指标最优和折衷最优解,如表1所示。
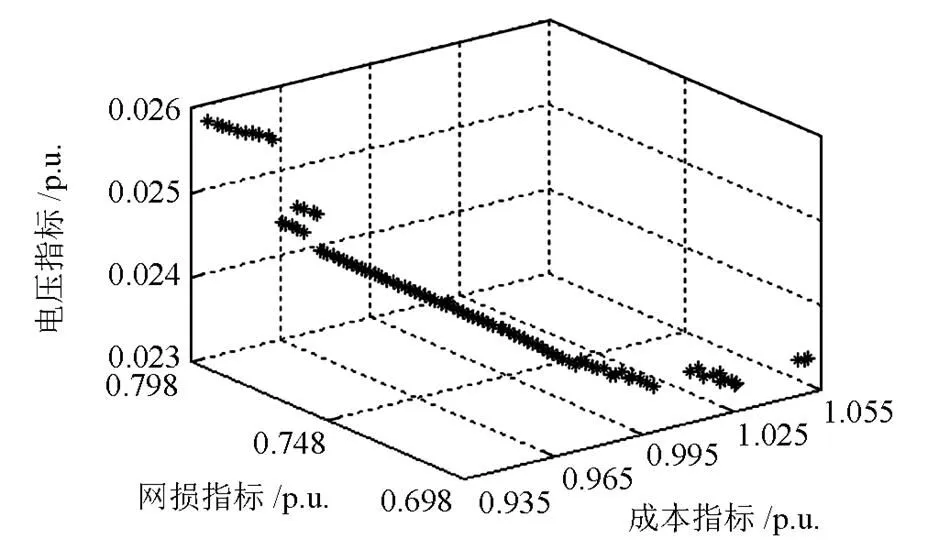
图1 三个目标函数的Pareto解集分布图

表1 不同目标对应的优化方案
从表1中可以看出,当成本指标最优时,优化配置方案中只有WG,而没有PV,这是由于当前光伏发电成本还比较高,在经济性方面处于劣势。通过比较成本指标最优配置方案、网损指标最优配置方案可以看出,成本指标与网损指标、电压指标存在明显的冲突,当成本指标最优时,网损指标、电压指标较差。利用信息熵得到的各个属性权重系数为C=0.402,P=0.316,V=0.282,代入式(18)可以得到折衷最优解。折衷最优解与优化配置前相比,全年成本值下降了0.16%,全年网损期望值下降了29.12%,全年电压偏差期望值下降了0.007 7 p.u.,说明了基于熵的模糊多属性决策方法能够较好地协调各个目标。
针对表1中网损指标最优的优化配置方案,将方案中14节点PV倾角变化,得到倾角与网损指标的关系见图2。从图中可以看出,对于固定式光伏方阵,PV倾角对网损指标有一定的影响,因此,在实际优化配置过程中,应该将倾角也作为决策变量加入到目标函数中去才能得到较为精确的结果。

图2 PV倾角与网损的关系曲线
对于表1中折衷最优解方案,优化配置前后各个时间段网损期望值比较和电压期望值比较分别见图3和图4。从图中可以看出,DRR接入电网后,每个时间段网损期望值和电压偏差期望值下降都很明显。当采用折衷最优方案,节点电压最大越限概率出现在节点28,为电压上限越限。
为了研究不同置信水平对优化结果的影响,本文将V和L取相同的值,分别设置为1、0.96和0.98,计算结果见表2。从表中可以看出,随着置信水平的下降,三个优化指标都能够得到不同程度的提高,因此,在实际规划过程中,需要权衡风险和收益之间的关系。

图3 优化配置前后各个时间段网损期望值比较

图4 优化配置前后各个时间段电压偏差期望值比较

表2 不同置信水平对应的优化结果
5 结语
本文针对WG和PV方阵联合优化配置问题,综合考虑成本、网损和电压指标,建立了多目标机会约束规划模型,通过IEEE-33节点配电网络算例分析,得到以下结论:
(1) 采用了精确的WG和PV发电模型,并将PV倾角作为决策变量代入运算,结果表明,PV倾角对最终方案有一定的影响;
(2) 蒙特卡洛法能够较好地模拟实际运行情况,体现风速、太阳辐射和负荷之间的相关性,多区间划分、建立概率密度的方法可以减少抽样次数;
(3) 机会约束规划模型将目标函数和约束条件分别用期望和概率的形式表示,能够较好地处理风速和太阳辐射的不确定性;
(4) 多目标微分进化算法和基于熵的模糊多属性决策方法适用于求解多目标优化问题。
[1] GEORGILAKIS P S, HATZIARGYRIOU N D. Optimal distributed generation placement in power distribution networks: models, methods, and future research[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3420-3428.
[2] EVANGELOPOULOS V A, GEORGILAKIS P S. Optimal distributed generation placement under uncertainties based on point estimate method embedded genetic algorithm[J]. IET Generation, Transmission & Distribution, 2014, 8(3): 389-400.
[3] 赵金利, 于莹莹, 李鹏, 等. 一种基于锥优化的DG优化配置快速计算方法[J]. 电工技术学报, 2014, 29(12): 173-179.
ZHAO Jinli, YU Yingying, LI Peng, et al. A fast determination method of DG capacity in distribution network based on conic programming[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 173-179.
[4] 张跃, 杨汾艳, 曾杰, 等. 主动配电网的分布式电源优化规划方案研究[J]. 电力系统保护与控制, 2015, 43(15): 67-72.
ZHANG Yue, YANG Fenyan, ZENG Jie, et al. Research of distributed generation optimization planning for active distributed network[J]. Power System Protection and Control, 2015, 43(15): 67-72.
[5] SINGH D, VERMA K S. Multiobjective optimization for DG[J]. IEEE Transactions on Power Systems, 2012, 24(1): 427-436.
[6] 张沈习, 陈楷, 龙禹, 等. 基于混合蛙跳算法的分布式风电源规划[J]. 电力系统自动化, 2013, 37(13): 76-82.
ZHANG Shenxi, CHEN Kai, LONG Yu, et al. Distributed wind generator planning based on shuffled frog leaping algorithm[J]. Automation of Electric Power Systems, 2013, 37(13): 76-82.
[7] 张蕴昕, 孙运全. 混合储能在风光互补微网中的控制策略[J]. 电力系统保护与控制, 2015, 43(21): 93-98.
ZHANG Yunxin, SUN Yunquan. Control strategy of a hybrid energy storage in wind-solar hybrid generation micro-grid[J]. Power System Protection and Control, 2014, 43(21): 93-98.
[8] 郭力, 王蔚, 刘文建, 等. 风柴储海水淡化独立微电网系统能量管理方法[J]. 电工技术学报, 2014, 29(2): 113-121.
GUO Li, WANG Wei, LIU Wenjian, et al. The energy management method for stand-alone wind/diesel/battery/ sea-water desalination microgrid[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 113-121.
[9] 姚致清, 张茜, 刘喜梅. 基于PSCAD/EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制, 2010, 38(17): 76-81.
YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J]. Power System Protection and Control, 2010, 38(17): 76-81.
[10] 程泽, 董梦男, 杨添剀, 等. 基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报, 2014, 29(9): 245-252.
CHENG Ze, DONG Mengnan, YANG Tiankai, et al. Extraction of solar cell model parameters based on self- adaptive chaos particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 245-252.
[11] ATWA Y M, EL-Saadany E F, SALAMA M M A. Optimal renewable resources mix for distribution system energy loss minimization[J]. IEEE Transactions on Power Systems, 2010, 25(1): 360-370.
[12] 杨琦, 张建华, 刘自发, 等. 风光互补混合供电系统多目标优化设计[J]. 电力系统自动化, 2009, 33(17): 86-90.
YANG Qi, ZHANG Jianhua, LIU Zifa, et al. Multi- objective optimization of hybrid PV/wind power supply system[J]. Automation of Electric Power Systems, 2009, 33(17): 86-90.
[13] YONG W, ZIXING C. Combining multiobjective optimization with differential evolution to solve constrained optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(1): 117-134.
[14] 刘志勇, 刘杨华, 林舜江, 等. 基于模糊多目标协调优化的配电网络重构研究[J]. 电力系统保护与控制, 2014, 42(4): 133-138.
LIU Zhiyong, LIU Yanghua, LIN Shunjiang, et al. Fuzzy multi-objective coordination optimization for distribution network reconfiguration[J]. Power System Protection and Control, 2014, 42(4): 133-138.
[15] NARIMANI M R, VAHED A A, AZIZIPANAH- ABARGHOOEE R, et al. Enhanced gravitational search algorithm for multi-objective distribution feeder reconfiguration considering reliability, loss and operational cost[J]. IET Generation, Transmission & Distribution, 2014, 8(1): 55-69.
(编辑 魏小丽)
Multiobjective chance-constrained programming method for wind generations and photovoltaic allocating
XIA Shu1, GU Jinyue1, GE Xiaolin2, QIAN Yaoxing1
(1. Shibei Electricity Supply Company, State Grid Shanghai Municipal Electric Power Company, Shanghai 200072, China;2. College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China)
A multi-objective planning scheme based on chance-constrained programming and Monte-Carlo method for wind generations and photovoltaic allocating is proposed to deal with the randomness and relevance of wind speed, solar radiation, and load. In the mathematic model, three indexes are introduced to evluate distributed generation profits, namely cost index, power loss index and voltage deviation index. Monte-Carlo method costs large computation time, therefore a method of established probability distribution based on multi-interval division is introduced to reduce the number of sampling. In the process of solving the model, the first multiobjective differential evolution is employed to get a set of pareto optimal solutions, then fuzzy multi-attribute decision making method based on information entropy is adopted to select the best compromise solution from the pareto optimal solutions. The case studies are carried out on the IEEE-33 nodes distribution network, and the results show that the prosed optimal model is rational, and the algorithm is effective.
wind generations; photovoltaic; optimal allocating; Monte-Carlo method; chance-constrained programming; multi-objective optimization
10.7667/PSPC150901
上海市青年科技英才扬帆计划(15YF1404600)
2015-05-30;
2015-10-11
夏 澍(1987-),男,博士,工程师,研究方向为电力系统规划与运行;E-mail: 870828@ncepu.edu.cn 顾劲岳(1981-),男,学士,技师,研究方向为电力系统规划与可靠性;葛晓琳(1987-),女,博士,讲师,研究方向为电力系统规划与运行。

