基于分解降阶模型的双馈异步发电机模态估计方法
王 清,薛安成,毕天姝,霍建东
基于分解降阶模型的双馈异步发电机模态估计方法
王 清1,薛安成1,毕天姝1,霍建东2
(1.华北电力大学新能源电力系统国家重点实验室,北京 102206;2.国网天津市电力公司,天津 300399)
了解双馈异步发电机的本征特性对于揭示其对电力系统稳定性影响的机理具有重要意义。传统本征特性研究方法基于双馈异步发电机详细模型分析模态,方程阶数高、计算量大,且分析结果缺乏有效验证手段。根据状态变量特征及其耦合特性,提出基于分解降阶模型的重要模态估计方法。首先基于机械传动链模型和异步发电机模型方程,分析了机械传动链和异步发电机状态变量与双馈异步发电机系统其他状态变量的多时间尺度和耦合特性。在此基础上,提出了基于分解降阶模型的轴系扭振和定转子磁链振荡模态的估计方法,并利用奇异摄动理论揭示了该降阶模态估计方法的内在本质。最后,通过对比分析分解降阶模态估计、详细模型模态分析结果,验证了分解降阶模态估计方法的正确性。
双馈异步发电机;本征特性;模态分类;模态降阶估计;奇异摄动理论
0 引言
随着电网中风电机组装机容量的日益扩大,特别是并网双馈异步发电机的不断增加,其对电力系统稳定性的影响愈发突出[1-4]。
揭示并网双馈风电对电力系统稳定性的影响机理,首先需要了解双馈异步发电机的动态行为特征。值得注意的是,双馈异步风机/风场与传统同步发电机具有显著的结构差异,上述结构差异带来了非线性模型及其动力学行为本征特征的改变。因此,诸多学者致力于研究双馈异步发电机的本征特性。
在宏观特征方面,研究表明,对于双馈异步发电机,在扰动中起主要作用的仍然是系统本征结构决定的主导振荡模态,即主导振荡模态将显著影响扰动后系统动态行为特性和稳定性[5-7]。
在研究方法上,双馈异步发电机的本征特性研究主要采用时域仿真法[8-11]和模态分析法[12-20]。其中,由于模态分析法可以从本征模态的角度定性和定量分析双馈异步发电机的特性而得到广泛应用。文献[12-15]分别针对双馈异步发电机的简化、详细数学模型,采用模态分析法分析了发电机平衡运行点、风力机参数、发电机参数、控制器参数对其模态特性的影响。文献[16-18]针对双馈异步发电机的详细数学模型进行了模态分析,并以参与因子大小作为忽略部分模态的依据对双馈异步发电机模型进行了降阶分析。文献[19]采用模态分析对DFIG控制器参数进行优化设计,从而改善DFIG的动态特性。文献[20]利用模态分析,研究了无刷双馈异步发电机的稳定运行域及发电机、控制器参数等对稳定域的影响。
现有文献在双馈异步发电机的本征特性研究方面取得了重要成果,但其研究都基于双馈异步发电机的详细模型,模型阶数高,计算量大,需要已知模型的完整参数,且计算结果的验证主要通过仿真定性校验,缺乏理论支撑。对于如何根据状态变量特征及其相互耦合特性,简化分析模型,获得重要模态鲜有涉及。有鉴于此,本文提出基于双馈异步发电机分解降阶模型的模态估计方法,该方法能够以较小的计算量得到双馈异步发电机的重要本征振荡模态,对于了解其本征特性和校验小扰动稳定分析或动态稳定分析中模态分析结果的正确性具有重要实用价值。
本文首先分析双馈异步发电机系统状态变量的多时间尺度和耦合特性,在此基础上提出轴系扭振模态和定转子磁链振荡模态的分解降阶估计方法,并利用奇异摄动理论揭示该方法的降阶本质,最后结合详细模型模态分析验证计算结果的正确性。
1 双馈异步发电机系统详细模型
图1为双馈异步发电机-无穷大系统,其中双馈异步发电机机械传动链、异步发电机、背靠背变换器、变换器控制、桨矩角控制和电网接口模型采用文献[5]中模型,锁相环采用文献[7]中二阶模型,该系统动态模型可用以下紧凑型一阶微分代数方程组描述。

式中:状态变量=[,t,r,b,ds,qs,d,q,DC,1,2,3,4,5,6,7,PLL,PLL]T;代数变量=[e,dr,qr,dr,qr,dg,qg,meas,meas,ds,qs,dg,qg,PLL]T;输入变量=[ref,t,,ref,ref,qg_ref,DC_ref]T。PLL为锁相环输出相位,PLL为锁相环状态变量,PLL为锁相环角速度,其他变量的含义参考文献[5]。
机械传动链和异步发电机数学模型描述如图1。

图1 双馈异步发电系统
1.1 机械传动链模型
双馈异步发电机的机械传动链采用2质量块等效模型时,其数学模型为
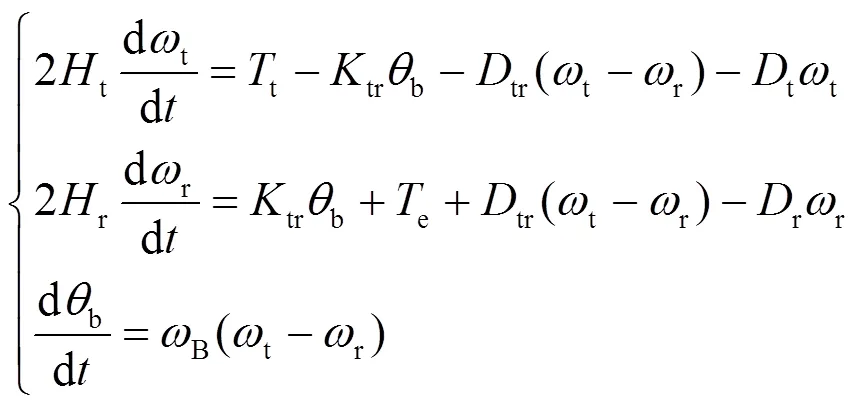
1.2 异步发电机模型
同步旋转坐标下,采用电动机惯例,异步发电机暂态模型可表示为

式中,r为发电机转子角速度,其他变量含义参考文献[5]。
2 多时间尺度及耦合特性分析
对于双馈异步发电机系统模型,即式(1),其中机械传动链对应状态变量变化慢,时间尺度为几秒;变换器控制和锁相环状态变量时间尺度为几十到几百毫秒;定转子磁链和直流支撑电容状态变量变化较其他状态变量快,其时间尺度为几毫秒甚至更短。同时,结合方程(2)和e表达式可知机械传动链状态变量t、r、b仅与异步发电机状态变量ds、qs、d、q耦合;异步发电机状态变量ds、qs、d、q仅与状态变量1、2、3、4、PLL、PLL耦合。综上可知,双馈异步发电机系统状态变量时间尺度范围很广,各组成部分的时间尺度如表1所示,且各部分对应状态变量间具有不同的相互耦合作用。

表1 DFIG各组成部分时间尺度
对双馈异步发电机系统模型式(1)在平衡点处进行线性化并将代数变量增量方程Δ代入可得

其中
式中,为单位阵。
根据表1所示双馈异步发电机各组成部分状态变量的多时间尺度特性,可将式(4)改写为

式中:1=[t,r,b]T为慢状态变量;2=[ds,qs,d, Δq]T为快状态变量;3=[,DC,1,2,3,4,5,6,7,PLL,PLL]T为中状态变量或与1和2弱耦合的状态变量。
另一方面,状态变量的时间尺度特性及耦合特性可由双馈异步发电机系统线性化模型的状态矩阵特征值、参与因子和矩阵元素体现。其中,特征值实部或虚部绝对值较大,其对应主导状态变量为快状态变量;特征值实部或虚部绝对值较小,其对应主导状态变量为慢状态变量。同时,若状态矩阵中元素很小或为零,则对应状态变量间为弱耦合。
3 模态降阶估计
根据线性化模型式(4)可计算双馈异步发电机系统所有特征值,然而该方程阶数高、计算量大。根据第2节可知机械传动链及异步发电机状态变量与双馈异步发电机控制其弱耦合,且机械传动链与异步发电机状态变量时间尺度具有显著差异。因此,本节将根据上述多时间尺度及弱耦合特性,在保留原系统本质特征的前提下,对轴系扭振模态和定转子磁链振荡模态进行降阶估计。
3.1 轴系扭振模态的降阶估计
轴系扭振模态由传动链模型式(2)决定,其相关状态变量为1=[t,r,b]T。由于式(2)中自阻尼系数t、r很小,可忽略不计,因此,式(2)可简化为

将式(6)线性化,并化为矩阵形式的增量方程,则
(7)
式中,为微分算子。进一步,根据式(7)的特征方程可得其非零特征值为

式(8)表明两质块模型中存在频率为n的扭振,n如式(9)。
(9)
3.2 定转子磁链振荡模态的降阶估计
定转子磁链振荡模态由异步发电机模型式(3)决定,其相关状态变量为2=[ds,qs,d,q]T。
正常运行时,考虑到DFIG中锁相环能够快速跟踪电网频率,即有PLL≈s。同时,由于定转子磁链暂态远快于DFIG转子转速的变化及转子侧变换器控制的响应速度,因此可以忽略r、qr、dr的变化,进而根据双馈异步发电机定转子电磁暂态4阶微分方程式(3),并对其线性化,可得定转子磁链暂态的增量方程为

根据微分方程组(10),可得其特征方程为
(11)
求解特征方程式(11),即可得到定转子磁链暂态振荡模态的估计值。
4 模态降阶估计合理性分析
本节采用奇异摄动理论对上述模态降阶估计的合理性进行分析。
为验证轴系扭振模态降阶估计的正确性,定义=Δ1、=[Δ2T, Δ3T]T(验证定转子磁链振荡模态时定义=[Δ1T, Δ3T]T、=Δ2),根据奇异摄动理论[21-22]可将式(5)改写为以下双时间尺度系统
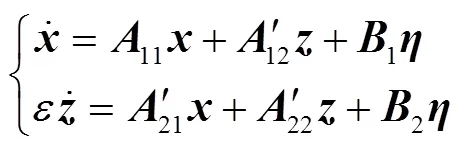
式中:为一小参数,且有=;=Δ。
为了研究式(12)的模态特性,根据奇异摄动理论,将状态变量和中的快速和慢速运动分别记以下标和,从而可将式(12)分解为两低阶子系统。
首先,令=0,忽略快状态变量变化对慢状态变量动态的影响,即认为在慢状态变量的过渡过程中,快状态变量的过渡过程早已达到了“拟稳态”,从而可得

(14)
其次,考虑到快动态过程中,慢变量变化很微小,即认为在快变量的过渡过程中,慢变量还未来得及发生变化,=s=常数,从而可得

由于f=-s,f=-s,f=-s,因此可得快子系统为
(16)
从而式(12)中状态变量特性可由子系统(14)和(16)综合得到。
(1) 轴系扭振模态估计
令=Δ1、=[Δ2T, Δ3T]T,则由式(14)和式(16)可得式(2)中机械传动链慢状态变量的动态可近似为

其中
(18)
忽略自阻尼系数t、r,可知状态矩阵0与式(6)中状态矩阵相等。因此,轴系扭振模态可由慢子系统状态矩阵0估计得到。
(2) 定转子磁链振荡模态估计

其中
(20)

5 算例分析
在Matlab中搭建了图1所示DFIG-无穷大系统详细模型,DFIG及控制器参数和稳态运行初值见附录。
根据系统状态矩阵可得与机械传动链状态变量相关和与异步发电机状态变量相关的矩阵分别如图2和图3所示。
图2中矩阵第1、8~18行的元素为零,表明状态变量1=[t,r,b]T与状态变量q及3=[,DC,1,2,3,4,5,6,7,PLL,PLL]T不耦合。仅有第2~7行的元素为不为零,表明状态变量1=[t,r,b]T仅与状态变量ds、qs和d耦合。这与第2节的分析一致。

图2 与机械传动链状态变量Δx1相关的矩阵

图3 与异步发电机状态变量Δx2相关的矩阵
图3中矩阵第1、2、4、9、14~16行的元素均为零,表明状态变量ds、qs、d、q与状态变量、t、b、DC、5、6、7不耦合。仅有第3、5~8、10~13、17~18行的元素为不全为零,表明状态变量ds、qs、d、q仅与状态变量r、1、2、3、4、PLL、PLL耦合。这与第2节的分析一致。
通过Matlab对图1所示系统详细模型进行小扰动分析可得其轴系扭振模态为−0.640 4±17.160 4i,其模值小于0.1倍定转子磁链振荡模态−2.3521±314.04i的模态,表明传动链状态变量t、r、b时间尺度远小于异步发电机状态变量ds、qs、d、q。因此,采用奇异摄动理论获得慢子系统过程中可假设摄动参数=|−0.640 4±17.160 4i|/|−2.352 1±314.04i|=1/18.3,进而得到机械振荡模态估计值。
同样地,与定转子磁链振荡模态耦合的模态中,模值最大为|-76.400 8|,因此,采用奇异摄动理论获得快子系统过程中可假设摄动参数=|-76.400 8|/|−2.352 1±314.04i|=1/4.1,进而得到定转子磁链振荡模态估计值。
由降阶模型计算得到的振荡模态估计值与根据详细模型计算得到的结果对比情况如表2所示。
表2结果表明:根据式和式得到的轴系扭振模态和定转子磁链振荡模态估计值与详细模型的Maltab特征值计算误差很小,从而,验证了振荡模态估计的正确性,并从一定程度上验证了双馈异步发电机组详细模型模态分析的正确性。

表2 轴系扭振和定转子磁链振荡模态计算结果对比
6 结论
本文根据双馈异步发电机系统状态变量多时间尺度及耦合特性,提出了基于分解降阶模型的双馈异步发电机重要模态估计方法,并通过奇异摄动理论揭示了该方法的内在本质,最后,通过对比分析分解降阶模态估计结果和详细模型模态分析结果验证了该方法的正确性。研究表明双馈异步发电机轴系扭振模态与定转子磁链振荡模态间具有时间尺度解耦特性,其中轴系扭振模态主要与慢状态变量相关,可由慢子系统降阶模型估计;定转子磁链振荡模态主要与快状态变量相关,可由快子系统降阶模型估计。
本文提出的分解降阶模态估计对于校验动态稳定分析中特征值计算结果的正确性具有重要参考价值,同时能够一定程度上了解双馈异步发电机系统主导振荡模态特性,有助于揭示扰动冲击下双馈异步发电机的动力学行为本征特性。
附录
在图1所示双馈异步发电机-无穷大系统中,风电机组额定功率B=1.5 MW,B=690 V,机组及控制系统参数如表3所示。

表3 双馈异步发电机及其控制器参数
风电机组稳态运行初值(标幺值)如表4所示。

表4 双馈变速风力风电机-无穷大系统参数
[1] SLOOTWEG J G, KLING W L. The impact of large scale wind power generation on power system oscillations[J]. Electric Power Systems Research, 2003, 67(1): 9-20.
[2]王境彪, 希望·阿不都瓦依提, 晁勤, 等. 双馈风电场接入交流或交直流混合系统低频振荡模态对比分析[J]. 电力系统保护与控制, 2015, 43(13): 23-29.
WANG Jingbiao, XIWANG Abuduwayiti, CHAO Qin, et al.Modal contrastive analysis of the low-frequency oscillation of AC and AC/DC hybrid system integrated by DFIG- based wind farms[J]. Power System Protection and Control, 2015, 43(13): 23-29.
[3] 边晓燕, 耿艳, 李学武, 等. 风电并网系统小干扰概率稳定性分析与改善[J]. 电力系统保护与控制, 2015, 43(20): 1-7.
BIAN Xiaoyan, GENG Yan, LI Xuewu, et al. Probabilistic small-signal stability analysis and improvement of power system with wind farm integration[J]. Power System Protection and Control, 2015, 43(20): 1-7.
[4] GAUTAM D, VITTAL V, HARBOUR T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1426-1434.
[5] WU F, ZHANG X P, GODFREY K. Small signal stability analysis and optimal control of a wind turbine with doubly fed induction generator[J]. IET Generation, Transmission & Distribution, 2007, 1(5): 751-760.
[6] ZHU S, VITTAL V, KLIEMANN W. Analyzing dynamic performance of power systems over parameter space using normal forms of vector fields — part 2: comparison of the system structure[J]. IEEE Transactions on Power Systems, 2001, 16(3): 451-455.
[7] 王志文, 沈沉, 刘锋. 不同锁相机制的双馈电机对电力系统小干扰稳定的影响分析[J]. 中国电机工程学报, 2014, 34(34): 6167-6176.
WANG Zhiwen, SHEN Chen, LIU Feng. Analysis on impact of doubly fed induction generations with different phase lock mechanism on power system small signal stability[J]. Proceedings of the CSEE, 2014, 34(34): 6167-6176.
[8] EKANAYAKE J B, HOLDSWORTH L, WU X G, et al. Dynamic modeling of doubly fed induction generator wind turbines[J]. IEEE Transactions on Power Systems, 2003, 18(2): 803-809.
[9] 齐尚敏, 李凤婷, 何世恩, 等. 具有低电压穿越能力的集群接入风电场故障特性仿真研究[J]. 电力系统保护与控制, 2015, 43(14): 55-62.
QI Shangmin, LI Fengting, HE Shien, et al. Research on fault characteristics of grid-connected large scale wind farms with LVRT capability[J]. Power System Protection and Control, 2015, 43(14): 55-62.
[10]刘其辉, 韩贤岁. 双馈风电机组的通用型机电暂态模型及其电磁暂态模型的对比分析[J]. 电力系统保护与控制, 2014, 42(23): 89-94.
LIU Qihui, HAN Xiansui. Comparative study on electromechanical and electromagnetic transient model for grid-connected DFIG[J]. Power System Protection and Control, 2014, 42(23): 89-94.
[11] HAO Z H, YAO Z Q, et al. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Technical Gazette, 2015, 22(1): 43-49.
[12]田春筝, 李琼林, 宋晓凯. 风电场建模及其对接入电网稳定性的影响分析[J]. 电力系统保护与控制, 2009, 37(19): 46-51.
TIAN Chunzheng, LI Qionglin, SONG Xiaokai. Modeling and analysis of the stability for the power system considering the integration of the wind farms[J]. Power System Protection and Control, 2009, 37(19): 46-51.
[13]MEI F, PAL B. Modal Analysis of grid-connected doubly fed induction generators[J]. IEEE Transactions on Energy Conversion, 2007, 22(3): 728-736.
[14]MISHRA Y, MISHRA S, LI F X, et al. Small-signal stability analysis of a DFIG-based wind power system under different modes of operation[J]. IEEE Transactions on Energy Conversion, 2009, 24(4): 972-982.
[15]李军军, 吴政球. 考虑感应电机机械暂态过程的风电系统的小扰动分析[J]. 电力系统保护与控制, 2011, 39(7): 14-19.
LI Junjun, WU Zhengqiu. Small signal analysis of wind power system considering induction motor mechanical transient process[J]. Power System Protection and Control, 2011, 39(7): 14-19.
[16]ROUCO L, ZAMORA J L. Dynamic patterns and model order reduction in small-signal models of doubly fed induction generators for wind power applications[C] // IEEE Power Engineering Society General Meeting, 2006.
[17]PAL B C, MEI F. Modelling adequacy of the doubly fed induction generator for small-signal stability studies in power systems[J]. IET Proceedings on Renewable Power Generation, 2008, 2(3): 181-190.
[18]舒进, 都劲松, 王靖程, 等. 基于奇异摄动降阶的风电接入系统阻尼分析[J]. 电力系统保护与控制, 2014, 42(19): 18-25.
SHU Jin, DU Jinsong, WANG Jingcheng, et al. System damping analysis after wind power integration using singular perturbation system reduction[J]. Power System Protection and Control, 2014, 42(19): 18-25.
[19]林今, 李国杰, 孙元章, 等. 双馈风电机组的小信号分析及其控制系统的参数优化[J]. 电力系统自动化, 2009, 33(5): 86-90.
LIN Jin, LI Guojie, SUN Yuanzhang, et al. Small-signal analysis and control system parameter optimization for DFIG wind turbines[J]. Automation of Electric Power Systems, 2009, 33(5): 86-90.
[20]熊飞, 王雪帆, 张经纬, 等. 无刷双馈电机的小信号模型稳定性分析[J]. 中国电机工程学报, 2009, 29(33): 117-123.
XIONG Fei, WANG Xuefan, ZHANG Jingwei, et al. Stability analysis of small signal model for brushless doubly-fed machine[J]. Proceedings of the CSEE, 2009, 29(33): 117-123.
[21]万百五, 吴受章. 大系统的模型简化[J]. 自动化学报, 1980, 6(1): 57-66.
WAN Baiwu, WU Shouzhang. Model reduction of large scale system[J]. Journal of Automation, 1980, 6(1): 57-66.
[22]席裕庚. 动态大系统方法导论[M]. 北京: 国防工业出版社, 1988.
(编辑 姜新丽)
A decomposed-reduced model based modes estimation method of DFIG
WANG Qing1, XUE Ancheng1, BI Tianshu1, HUO Jiandong2
(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Source, North China Electric Power University, Beijing 102206, China; 2. State Grid Tianjin Electric Power Corporation, Tianjin 300399, China)
Understanding the intrinsic characteristics of DFIG is of great importance to reveal the influencing mechanism of DFIGs on power system stability. The conventional analysis of intrinsic characteristics is based on the modal analysis for the detail model of DFIG and characterized by high-order equation and heavy computation. Besides, the results of the analysis lack effective validation. A method of reduced-order model based modes estimation is proposed according to the characteristics of state variables and their coupling property. The multi-time scale and coupling properties of the state variables of DFIG system is analyzed. And then, the reduced-order model based modes estimation of mechanical and rotor electrical oscillatory modes is proposed, and the essence of the method is analyzed using singular perturbation theory. In the end, the correctness of the reduced-order model based modes estimation is verified by comparing the mode results from decomposed-reduced model and detail model. This work is supported by National Basic Research Program of China (973 Program) (No. 2012CB215206) and National Natural Science Foundation of China (No. 51477050 and No. 51190103).
DFIG; intrinsic characteristics; modes classification; reduced-order model based modes estimation; singular perturbation theory
10.7667/PSPC150995
国家重点基础研究发展计划项目(973计划) (2012CB215206);国家自然科学基金(51477050, 51190103)
2015-06-14;
2015-11-05
王 清(1989-),男,博士研究生,主要研究方向为电力系统继电保护与控制等;E-mail: carowangqing@sina.com薛安成(1979-),男,博士,副教授,主要研究方向为电力系统分析与保护等;E-mail: acxue@ncepu.edu.cn 毕天姝(1973-),女,教授,主要研究方向为电力系统保护与控制、故障诊断等。E-mail: tsbi@ncepu.edu.cn

