基于改进混合抽样与最小切负荷计算的电力系统可靠性评估方法

孙腾飞，程浩忠，张立波，周勤勇，贺海磊，曾平良



基于改进混合抽样与最小切负荷计算的电力系统可靠性评估方法

孙腾飞1，程浩忠1，张立波1，周勤勇2，贺海磊2，曾平良2

(1.电力传输与功率变换控制教育部重点实验室(上海交通大学),上海 200240；2.中国电力科学研究院,北京 100192)

评估组合系统可靠性时，蒙特卡罗模拟法不受系统规模及非线性的影响，且结果准确的特性使其在大型电力系统可靠性评估中具有优越性。但为了获得精度较高的可靠性指标，其往往需要较长计算时间。针对这一问题，采用重要抽样法与离散拉丁超立方抽样相结合的方法，从减小样本方差与增加样本均匀性两方面提高蒙特卡罗模拟的收敛性。对于大规模发输电系统，运用灵敏度分析与线性规划相结合的方法进行系统过负荷校正，既能保证求解最优性又可以提高求解速度。将该算法应用于IEEE RTS79系统、IEEE RTS96系统和某电网500 kV及以上电压等级电力系统计算可靠性指标，验证了该算法的可行性。

改进离散拉丁超立方抽样；最小切负荷计算；电力系统；可靠性评估；蒙特卡罗模拟；灵敏度分析

0 引言

发输电系统可靠性评估方法主要分为解析法和模拟法。蒙特卡罗模拟(Monte Carlo simulation)通过产生随机数的方式模拟系统中各个元件的状态，通过抽样的方式对系统状态进行选择，用统计的方法得到可靠性指标[1-3]。蒙特卡罗模拟基于概率模型的特点，能够反映系统各种随机特性，得到可靠性指标的期望与方差值以及其在各种系统状态下的概率分布[4-5]。蒙特卡罗模拟法实际抽样次数一般远小于系统全部状态数的特点特别适合应用到迅速发展、网架不断扩大的大规模电力系统可靠性评估中[6-7]。

然而，蒙特卡罗模拟法的计算量与估计精度的平方成反比[8]，导致该方法将不得不牺牲大量时间来进行规模巨大的抽样计算来获得所需的计算精度[9]，这样一来，其收敛速度就受到了极大的限制。

为了解决这一问题，许多研究都在关注如何加快蒙特卡罗模拟收敛。文献[10-11]采用并行处理技术降低了计算时间；文献[12]提出采用网流规划代替潮流优化，通过简化系统分析和优化计算来加快评估速度；文献[13]对系统状态进行解析判断，同时通过有功潮流分布引导的方法来加快潮流分布修改，从而减少了计算量；文献[14]通过支持向量机的求解速度建立预测估算算法来加快评估速度。然而，这些方法对计算环境要求较高，也会带来在加快计算速度的同时导致计算精度下降等问题。

本文采用离散拉丁超立方抽样法与重要抽样方法[15-16]相结合的方法进行抽样，分别从减小样本方差和对样本空间进行均匀采样两方面提高蒙特卡罗模拟的收敛性。同时，采用灵敏度分析和线性规划[17]相结合的方法对系统进行过负荷校正，通过减少控制变量和支路容量约束的数量减小了问题的规模。在保证求解精度的基础上，该方法有效提高了蒙特卡罗模拟的计算速度。

1 系统状态的解析判断

1.1 发输电系统可靠性模型

蒙特卡罗模拟通过对设备概率分布函数进行抽样得到系统状态。由于电力系统中数量巨大的不确定因素会影响到系统的可靠性，因此只计入对系统运行状态起主导作用的因素。

在系统状态解析中，把发电机与输变电设备都作为只有停运和运行的两状态设备，通过计算机产生[0, 1]区间内服从均匀分布随机数的方式进行采样，把随机数与设备故障率进行比较得到该设备状态的解析判断。发输变电设备状态解析如式(1)所示，其状态组成了相应的状态向量。

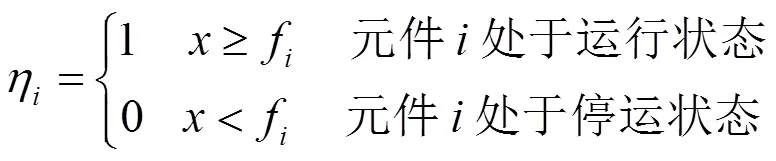
完成状态采样后，每个发电机节点与输变电设备都需要进行故障检测判断。如果没有故障，元件处于正常状态，标记为1；否则，标记为0。值得注意的是，如果备用容量的投入能使故障发电机节点有功功率不变，仍然标记其状态为1；只有在备用容量全部投入也不能完全补偿某节点发电机故障带来的有功功率损失时，该节点状态才会标记为0。这种系统状态解析判断方式能够使有功约束条件数下降到与发电机节点数持平，从而极大地降低了有功优化调整计算过程的维数。

1.2 特高压系统可靠性模型

特高压交流输电系统具有网络功能，可以根据电源与负荷分布、输送电力容量等实际需求构成特高压骨干网架。所以，特高压交流输变电设备可靠性模型与常规输变电设备相似，为两状态模型。

对于特高压直流输电系统，将其向电网的注入功率等效为多状态电源，本文蒙特卡罗模拟过程中，把它等效为一个多状态元件参与抽样。对直流系统等效元件状态的随机抽样同样通过比较[0, 1]区间均匀分布随机数与元件状态概率值来实现。对于降额运行状态，假设其注入功率在最小允许值和额定值之间均匀分布，降额运行注入功率计算如式(2)。

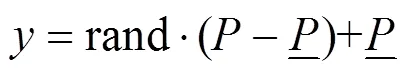
2 离散拉丁超立方重要抽样方法

2.1 离散拉丁超立方抽样

拉丁超立方抽样(Latin Hypercube Sampling, LHS)由样本生成和相关性控制两阶段构成。传统的LHS方法主要针对连续变量，而元件可靠性参数通常为离散分布的随机变量，为了使该方法有效应用于可靠性评估，Panida等提出了离散拉丁超立方抽样(Discrete Latin Hypercube Sampling, DLHS)方法[18]。

(1) 样本生成

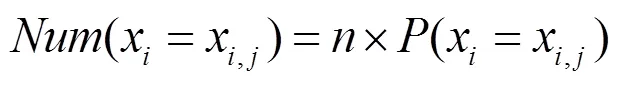
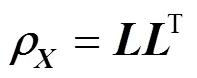
(2) 相关性控制

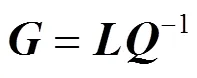
(6)

2.2 重要抽样法

重要抽样方法在不改变原有样本期望值的前提下，通过改变已有样本空间的概率分布，减小其方差，达到缩短计算时间的目的。概率分布更新后的分布函数被叫作重要分布函数。

系统重要分布函数的表达形式如式(7)所示。

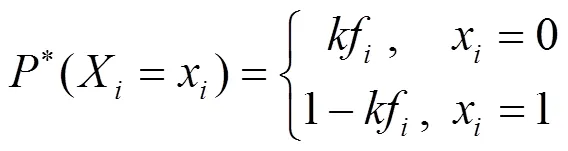
式中：为元件的强迫停运率；表示突出“重要事件”的重要乘子；为元件的状态取值。

2.3 离散拉丁超立方重要抽样法

重要抽样法通过减小样本空间方差的方式来加速蒙特卡罗模拟收敛，而离散拉丁超立方抽样法通过对样本空间进行均匀采样提高蒙特卡罗模拟的收敛性，因此将二者结合可以从两个不同的方面加速蒙特卡罗模拟的收敛。本文将该方法称之为离散拉丁超立方重要抽样法(Discrete Latin Hypercube Importance Sampling，DLHIS)，步骤如下：

1) 构造离散分布随机变量的重要分布函数；

7) 根据重要抽样函数计算原样本空间状态的期望值。

3 系统过负荷校正

3.1 常规过负荷校正方法

通常情况下采用线性规划方法[19]来进行系统过负荷校正。线性规划法针对设备随机故障、负荷随机波动引起的系统功率不平衡或者线路过负荷等情况，通过调整发电机出力或在某些负荷点进行一定负荷削减来消除这些不正常状态。

相对于线性方法，灵敏度分析法[20]也是在电力系统规划及运行控制决策中经常使用的方法。应用灵敏度方法进行系统状态校正时，灵敏度矩阵可以描述线路有功潮流与节点注入功率间的关系，指导发电机出力调整与系统负荷量的削减。

灵敏度分析方法属于启发式的方法，不能保证校正方案的最优性；线性规划方法虽然更为严格，但对于超大规模发输电系统，问题的规模很大，求解速度也会受到影响。因此，本文建立灵敏度分析与线性规划相结合的方法来进行系统过负荷校正。

3.2 灵敏度分析法与线性规划相结合法

电力系统中潮流问题多为非线性问题，而直流潮流能够将其简化为线性问题，从而可以很方便地进行计算分析。相比于交流潮流，其计算速度要快得多。在计算精度允许的前提下，本文在过负荷校正中采用直流潮流模型。

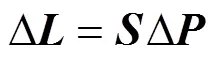
(9)

将线性规划法与灵敏度分析法相结合，建立如下线性规划模型：

目标函数：

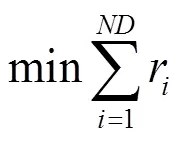
约束条件：

(11)

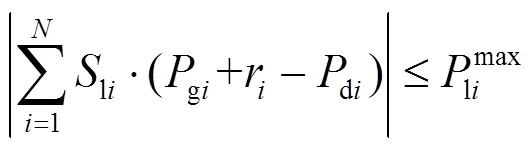
(13)

(14)

运用此模型，可以通过减小控制变量和支路容量约束条件的数量减小问题的规模。

首先对灵敏度矩阵进行奇异值分解，通过主成份分析，找出对消除过载最有效的发电机和负荷节点作为控制变量集(和)，在约束中只考虑这些因素的作用。另外，式(12)中通过潮流筛选，只考虑重载和过载支路约束的影响；通过实际运行校验，把超过线路容量65%的支路定义为重载支路，可以保证计算的精确度。通过灵敏度分析对约束条件进行降维处理，可以大大减小问题的规模。算例分析计算结果表明，本文过负荷校正方法通过对节点与支路的筛选，极大地减小了问题规模，较传统线性规划方法计算速率得到了进一步提高。

本文对系统可靠性评估流程如图1所示。

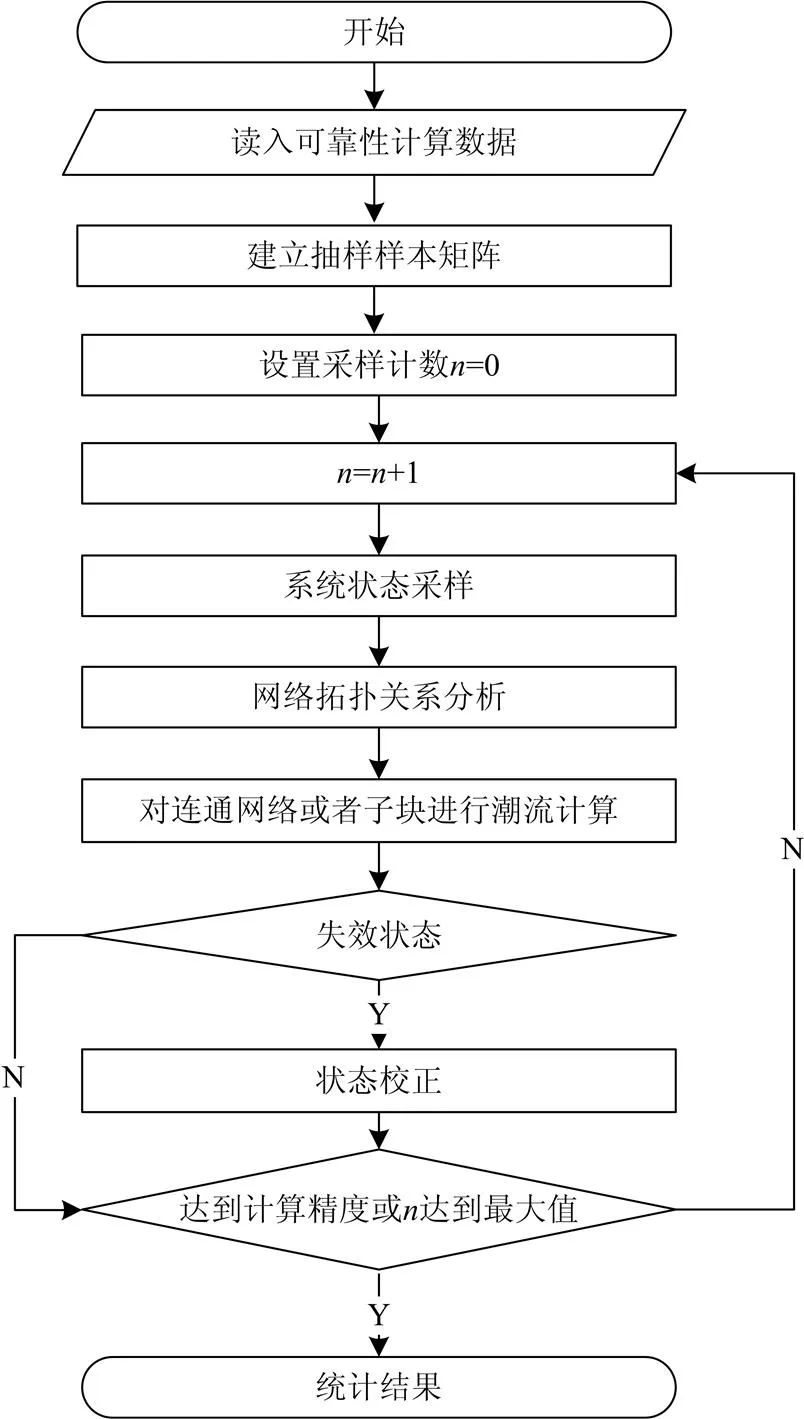
图1 基于改进拉丁超立方抽样的可靠性评估流程

4 算例分析

发输电系统可靠性评价一般通过计算负荷削减概率(Loss of Load Probability，LOLP)、切负荷持续时间(Expected Duration of Load Curtailments，EDLC)、电力不足期望值(Expected Demand Not Supplied，EDNS)、电量不足期望值(Expected Energy Not Supplied，EENS)、电量不足期望占该系统峰值负荷量的比率(Bulk Power/Energy Curtailment Index，BPECI)和系统严重性指标(Severity Index，SI)六个指标对电力系统可靠性进行评估。对于发输电元件，采用本文提出的混合抽样方法进行抽样来加速蒙特卡罗模拟收敛；另外，由于本文在切负荷计算时采用了灵敏度分析与线性规划相结合的方法减小问题规模以加速计算，因此在结果分析中加入计算时间指标，通过与传统线性优化切负荷计算算法对比，表明本文方法计算的速度优势。

上述可靠性指标中，EDNS的收敛速度较慢，因此采用式(15)所示的EDNS的方差系数作为算法的收敛判据，以其达到0.01作为迭代终止条件。

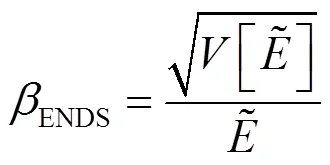
需要注意的是，在蒙特卡罗模拟过程中，混合抽样中的离散拉丁超立方抽样需要在确定的抽样次数下比较的大小来体现不同抽样方法的收敛速度。因此，在可靠性指标计算完成之后，从本文方法所得到的系统方差系数随采样次数变化曲线中，找到方差系数下降显著变慢的转折点作为传统抽样方法与本文提出的离散拉丁超立方重要抽样方法的检验抽样次数，比较相同抽样次数下两种抽样方法所得到的大小，以此来表明本文提出的混合抽样方法对抽样过程收敛的促进作用。

把本文算法应用于IEEE RTS79系统、IEEE RTS96系统和某电网500 kV及以上电压等级电力系统，将计算结果同传统算法结果进行对比，以验证本文算法的正确性以及对计算的加速效果。

需要指出的是，为了证明本文算法对计算的加速作用，需要对比两种算法的计算时间。下文所列出的计算时间均是在CPU为Pentium(R) Dual-Core、E5800@3.2 GHz，内存2.00 GB的计算机上得到的。

4.1 重要乘子对收敛性的影响

本文在抽样中结合了基于重要乘子的重要采样方法，重要乘子的选取对算法收敛性有很大影响。本文在预先选定基准乘子前提下，通过在一定范围内改变重要乘子的大小，观察算法收敛性与乘子的关系，从而确定最优乘子。在IEEERTS79系统中，算法迭代次数与乘子的关系如图2所示。

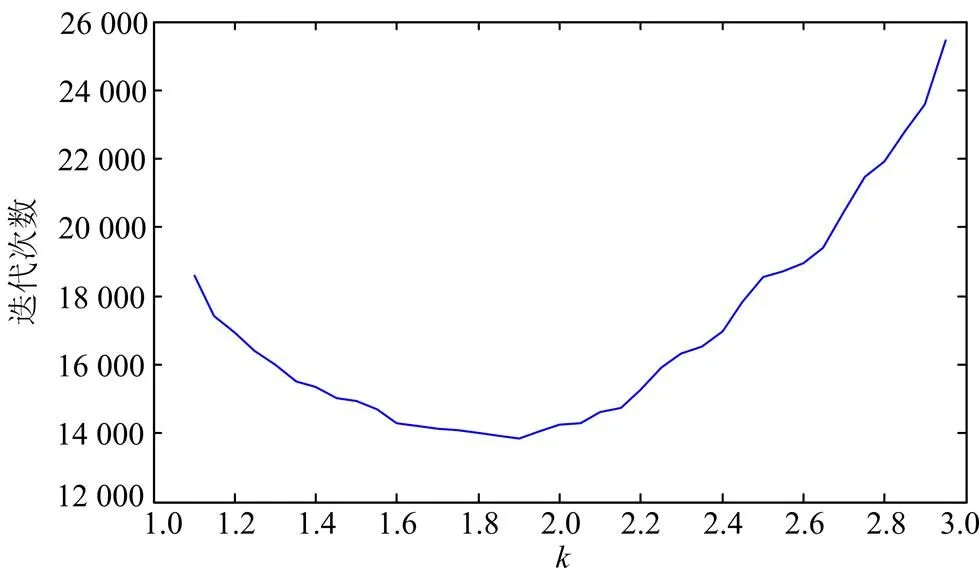
图2 算法迭代次数与重要乘子k的关系图

上图中横坐标代表重要乘子数值，纵坐标代表迭代次数(次)。可见，当乘子较小时，随乘子增大，算法迭代次数呈整体减小趋势，收敛速度逐渐加快；当乘子达到1.8时，迭代次数与乘子变化关系趋于平坦，收敛速度虽然继续变快但趋于平缓；当乘子达到2.0之后，算法迭代次数会随着乘子增大而呈总体增加态势，收敛变慢。因此，抽样中对重要乘子的选取十分重要，需要选择最优乘子来保证算法最快达到收敛。在IEEE RTS79系统中，本文选取1.9作为最优重要乘子，该结果也在已有研究允许范围之内[21]。

4.2 IEEERTS79系统算例

IEEE RTS79系统共有24个节点，21条支路，32台机组，装机容量为3 405 MW，其中最大机组容量为400 MW，最小机组容量为12 MW，年最大负荷为2 850 MW[22]。

图3给出了算法在IEEE RTS79系统实现中方差系数随采样次数变化的曲线，其横坐标代表迭代次数(次)，纵坐标代表方差系数。由图可知当采样次数达到14 000次左右时，可靠性指标满足收敛条件。另外，在抽样次数达到2 000次时，曲线有一个明显的拐点，即方差系数显著下降。因此，在检验中，把2 000次作为离散拉丁超立方重要抽样方法与传统抽样方法的规定抽样次数，通过比较在该抽样次数下不同方法得到的值，表明本文混合抽样方法对抽样收敛的加速效果。

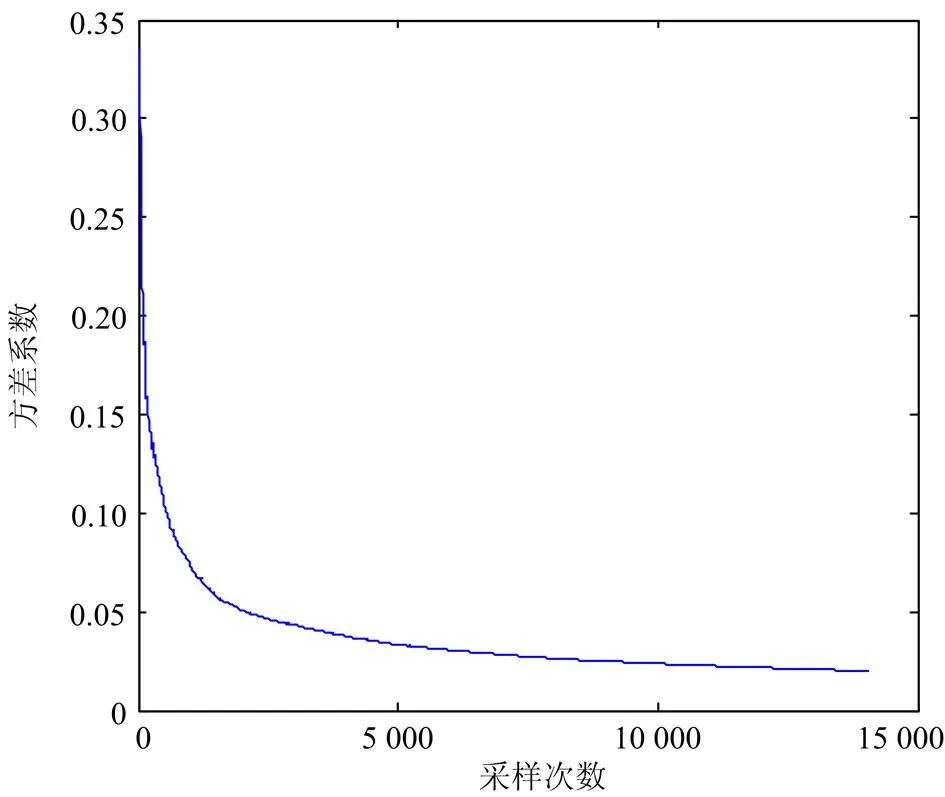
图3 IEEE RTS79系统方差系数随采样次数变化曲线

表1计算得出了本文算法在IEEE RTS79系统下的可靠性指标，计算结果与传统算法得到的数据基本相同。在可靠性分析中占重要地位的LOLP与EENS指标，本文计算结果与传统算法分别仅有1.36%与0.59%的偏差，表明本文算法的正确性。在最小切负荷计算时，通过对灵敏度矩阵的主成份分析，在该24节点系统下，只选取对消除过载最有效的两个节点与3条支路作为约束条件，约束条件个数大大减少，计算速度得以加快。另外，在2 000次抽样水平下，传统抽样方法得到的值为0.057 9，而本文混合抽样方法得到的值为0.054 3，下降了约6.63%。由此可见，本文混合抽样方法对收敛加速效果明显。最终计算结果表明，该系统下本文提出的可靠性评估算法计算时间约为传统算法的67%，在保证精度的前提下，极大地提高了计算效率。

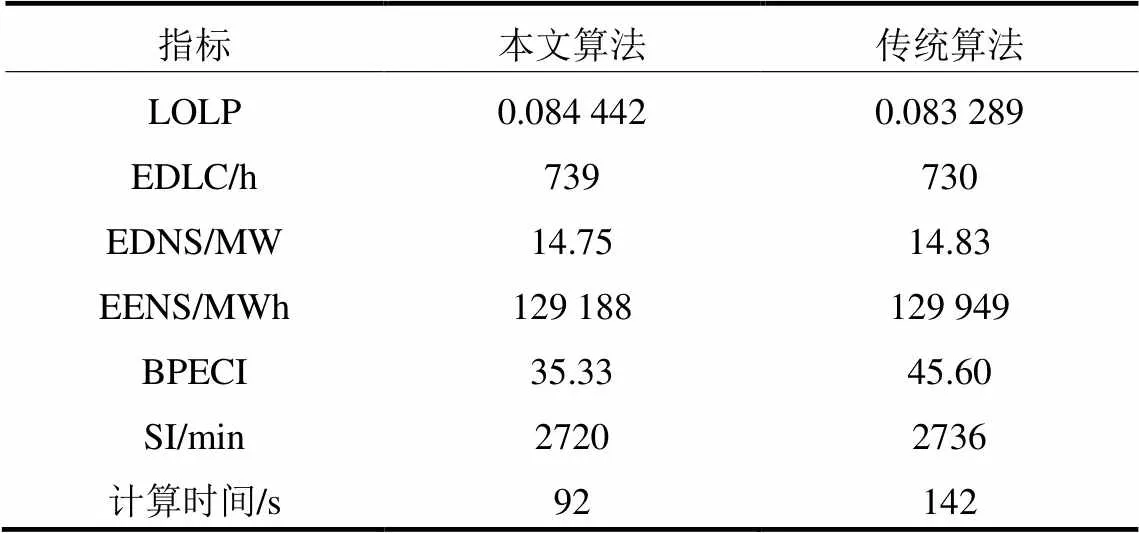
表1 IEEE RTS79系统可靠性指标

4.3 IEEE RTS96系统算例

IEEE RTS96系统由3个IEEE RTS79系统组合而成，共有73个节点，96台机组，装机容量为10 215 MW，其中最大机组容量为400 MW，最小机组容量为12 MW，年最大负荷为8 550 MW[23]。

在IEEE RTS96系统下，方差系数随采样次数的变化趋势与IEEE RTS79系统相似，选取2.6作为重要乘子，当采样次数接近50 000次时，可靠性指标满足既定收敛条件。对发输电元件状态采用本文提出的离散拉丁超立方重要抽样方法进行抽样，当抽样次数达到10 000次时，系统方差系数减小速率显著变慢，因此，把10 000次作为该系统下离散拉丁超立方重要抽样与传统抽样方法检验的规定抽样次数。

表2同样给出了本文算法在IEEE RTS96系统中的实现情况。不难发现，在系统规模扩大的情况下，蒙特卡罗模拟抽样次数也显著增加，从而传统可靠性评估方法将消耗大量的计算时间。由表中数据可以看出，在系统规模较大的情况下本文算法与传统算法计算得到的数据也基本相同，其中LOLP与EENS指标与传统算法结果分别只有0.92%与3.05%的偏差，也就是说，算法在规模扩大的系统中依旧保持较高的计算精度，本文混合抽样方法与改进过负荷校正方法具有有效性，在一般系统可靠性评估中，指标计算结果与实际情况基本一致。不仅如此，在较大规模的系统中传统算法要计及所有节点与线路，数据冗杂且计算量大，效率十分低下。而本文可靠性评估方法在加速蒙特卡罗模拟收敛的同时，最小切负荷计算时仅计入对消除过载影响较大的5个节点与7条支路，忽略大部分节点与支路的影响，达到大幅度减少约束条件个数的目的。在检验中，传统抽样方法与离散拉丁超立方重要抽样方法在10 000次抽样时得到的分别为0.081 1与0.075 9，本文提出的混合抽样方法得到的计算指标较传统方法下降了约6.85%，表明了本文抽样方法对抽样收敛的加速作用。计算结果表明，过负荷校正过程通过节点与支路筛选，本文提出的可靠性评估方法较传统算法节约了近40%的计算时间，加速效果更加显著，既保证了计算结果的有效性，又对提高计算效率具有可行性。

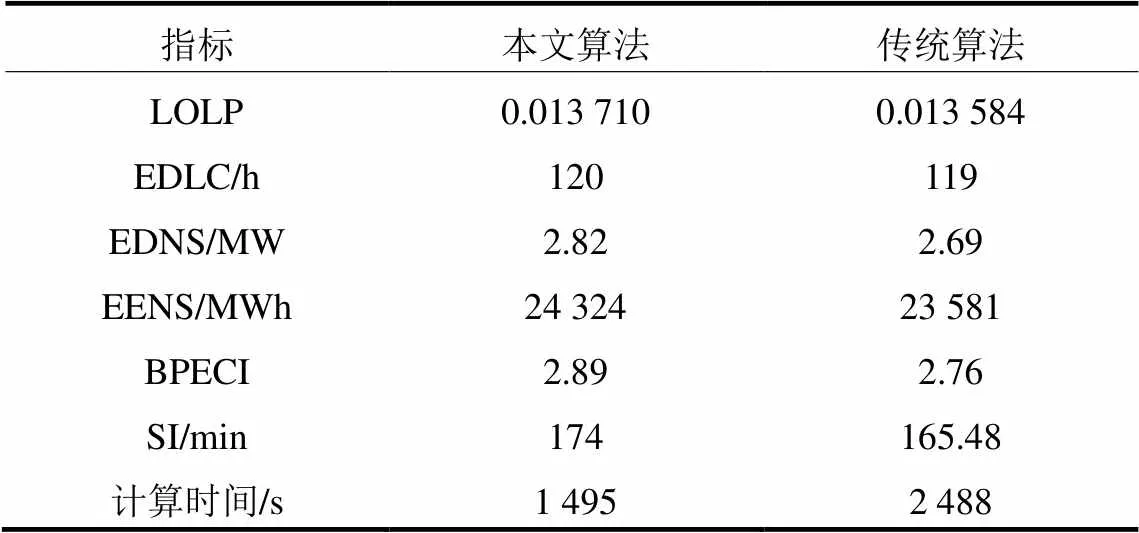
表2 IEEE RTS96系统可靠性指标

4.4 实际电网算例

本文选取某电网500 kV及以上电压等级系统作为实际系统测试对象。该系统包括318个节点与412条支路，网内发电机容量为184 240 MW，直流外来电容量为76 900 MW，特高压交流外来电容量为54 800 MW，线路走廊为387条，1 000 kV变电站(开关站)共15座。

系统中发输电与特高压元件按本文提出的混合抽样方法抽样。该系统500 kV及以上电网规模较大，传统算法在该规模系统实现中将不得不对所有节点与线路一一进行判断，这个过程计算量巨大且冗余，迭代完全收敛将耗时过长。表3数据表明传统算法在计算中耗费大量时间，效率低下，适应性较差，在较大规模系统中的使用存在一定限制。

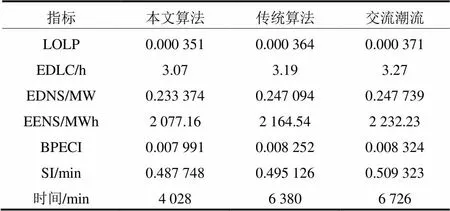
表3 某电网可靠性指标

由表3可以看出，在规模较大的实际系统中，本文算法与传统算法计算出的可靠性指标也基本一致，LOLP与EENS指标分别只相差3.5%与4.0%，与实际情况也基本相同，表明算法精度在较大规模系统中同样可以得到保证。同时，根据上文分析，在较大规模系统最小切负荷计算中，传统算法需要进行大量计算，而本文算法与之相比，超过75%的节点与支路都不计入约束条件中，最大限度地减小了问题规模。通过增加预先筛选步骤，极大地减少了计算量，仅用传统算法64%的时间便可完成计算，计算速度优势明显，应用效果较好。

另外，由于本文采用直流潮流模型，对问题进行了一定的简化，因此，在实际系统算例中，将本文方法与交流潮流下计算的可靠性指标也进行了对比分析。与交流潮流模型计算指标相比，本文方法得到的指标偏差略微增大，LOLP与EENS指标分别偏差5.4%与6.1%，偏差的增加是由于模型的简化造成的。但是，本文方法只需交流潮流模型60%的时间便可完成计算，虽然牺牲了一定的计算精度，但可以获得较高的计算效率。在实际电网可靠性评估中，本文结果的计算精度也是允许的，表明了本文方法具有有效性，且其高效率优势使其更有实际应用价值。

5 结语

本文从系统充裕性的角度对发输电组合系统可靠性评估进行了研究，并基于离散拉丁超立方抽样和重要抽样的混合抽样方法提出了发输电组合系统的可靠性评估方法，二者结合从对样本空间进行均匀采样和减小样本空间方差两个不同方面提高了蒙特卡罗模拟的收敛性。同时，采用了灵敏度分析法和线性规划相结合的方法进行了系统过负荷校正，通过对消除过载影响较大的节点与支路进行筛选，从减少控制变量和支路容量约束数量两方面最大程度地减小了问题的规模，使计算速度显著提高。与传统算法相比，本文提出的算法在保证评估结果准确的前提下极大地加快了可靠性指标计算速度，提高了计算效率。

[1] 刘文霞, 蒋程, 张建华, 等. 一种用于序贯蒙特卡罗仿真的风电机组多状态可靠性模型[J]. 电力系统保护与控制, 2013, 41(8): 73-80.

LIU Wenxia, JIANG Cheng, ZHANG Jianhua, et al. A multistage reliability model of wind turbines for sequential Monte Carlo simulation[J]. Power System Protection and Control, 2013, 41(8): 73-80.

[2] 张建华, 王昕伟, 蒋程, 等. 基于蒙特卡罗方法的风电场有功出力的概率性评估[J]. 电力系统保护与控制, 2014, 42(3): 82-87.

ZHANG Jianhua, WANG Xinwei, JIANG Cheng, et al. Probabilistic assessment of wind farm active power based on Monte-Carlo simulation[J]. Power System Protection and Control, 2014, 42(3): 82-87.

[3] BORGES C L T, FALCÃO D M, MELLO J C O, et al. Composite reliability evaluation by sequential Monte Carlo simulation on parallel and distributed processing environments[J]. IEEE Transactions on Power Systems, 2001, 16(2): 203-209.

[4] BILLINTON R, WANG P. Teaching distribution system reliability evaluation using Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 1999, 14(2): 397-403.

[5] LI W, ZHOU J, XIE K, et al. Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2008, 23(2): 336-343.

[6] PITT M K, SILVA R S, GIORDANI P, et al. On some properties of Markov chain Monte Carlo simulation methods based on the particle filter[J]. Journal of Econometrics, 2012, 171(2): 134-151.

[7] GELLY S, SILVER D. Monte-Carlo tree search and rapid action value estimation in computer[J]. Artificial Intelligence, 2011, 175(11): 1856-1875.

[8] 赵渊, 何媛, 芦晶晶. 旋转备用对电网可靠性的影响及优化配置研究[J]. 电力系统保护与控制, 2014, 42(8): 40-46.

ZHAO Yuan, HE Yuan, LU Jingjing. Allocation optimization of spinning reserve and its effect on bulk power systems reliability[J]. Power System Protection and Control, 2014, 42(8): 40-46.

[9] GONZÁLEZ-FERNÁNDEZ R A, LEITE DA SILVA A M. Reliability assessment of time-dependent systems via sequential cross-entropy Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2381-2389.

[10] 黄殿勋, 张文, 郭萍, 等. 发输电系统可靠性评估的蒙特卡洛改进算法[J]. 电力系统保护与控制, 2010, 38(21): 179-183.

HUANG Dianxun, ZHANG Wen, GUO Ping, et al. The Monte-Carlo improved method for reliability evaluation of generation and transmission systems[J]. Power System Protection and Control, 2010, 38(21): 179-183.

[11] 杨珍贵, 杜雄, 孙鹏菊, 等. 风电全功率变流器参数对可靠性的影响分析[J]. 电工技术学报, 2015, 30(16): 137-145.

YANG Zhengui, DU Xiong, SUN Pengju, et al. Analysis of effect of the converter parameters on full-rated wind power converters reliability[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 137-145.

[12] 熊小伏, 王建, 袁峻, 等. 时空环境相依的电网故障模型及在电网可靠性评估中的应用[J]. 电力系统保护与控制, 2015, 43(15): 28-35.

XIONG Xiaofu, WANG Jian, YUAN Jun, et al. Temporal and spatial environments dependent power grid failure method and its application in power grid reliability assessment[J]. Power System Protection and Control, 2015, 43(15): 28-35.

[13] 张硕, 李庚银, 周明. 含风电场的发输电系统可靠性评估[J]. 中国电机工程学报, 2010, 30(7): 8-14.

ZHANG Shuo, LI Gengyin, ZHOU Ming. Reliability assessment of generation and transmission systems integrated with wind farms[J]. Proceedings of the CSEE, 2010, 30(7): 8-14.

[14] ROCCO C M, MORENO J A. Fast Monte Carlo reliability evaluation using support vector machine[J]. Reliability Engineering & System Safety, 2002, 76(3): 237-243.

[15] 王晓滨, 郭瑞鹏, 曹一家, 等. 电力系统可靠性评估的自适应分层重要抽样法[J]. 电力系统自动化, 2011, 35(3): 33-38.

WANG Xiaobin, GUO Ruipeng, CAO Yijia, et al. A self-adapting stratified and importance sampling method for power system reliability evaluation[J]. Automation of Electric Power Systems, 2011, 35(3): 33-38.

[16] 黄江宁, 郭瑞鹏, 赵舫, 等. 电力系统可靠性评估中的分层均匀抽样法[J]. 电力系统自动化, 2012, 36(20): 19-24.

HUANG Jiangning, GUO Ruipeng, ZHAO Fang, et al. Stratified uniform sampling method for power system reliability evaluation[J]. Automation of Electric Power Systems, 2012, 36(20): 19-24.

[17] 余民, 杨旻宸, 蒋传文, 等. 风电并网后电力系统可靠性评估和备用优化研究[J]. 电力系统保护与控制, 2012, 40(12): 100-104, 135.

YU Min, YANG Minchen, JIANG Chuanwen, et al. Study on power system reliability and reserve optimization with wind power integration[J]. Power System Protection and Control, 2012, 40(12): 100-104, 135.

[18] JIRUTITIJAROEN P, SINGH C. Comparison of simulation methods for power system reliability indexes and their distributions[J]. IEEE Transactions on Power Systems, 2008, 23(2): 486-493.

[19] 陈雁, 文劲宇, 程时杰. 电网规划中考虑风电场影响的最小切负荷量研究[J]. 中国电机工程学报, 2011, 31(34): 20-27.

CHEN Yan, WEN Jinyu, CHENG Shijie. Minimum load- curtailment in transmission network planning considering integrated win farms[J]. Proceedings of the CSEE, 2011, 31(34): 20-27.

[20] WU P, CHENG H, XING J. The interval minimum load cutting problem in the process of transmission network expansion planning considering uncertainty in demand[J]. IEEE Transactions on Power Systems, 2008, 23(3): 1497-1506.

[21] 宋晓通, 谭震宇. 改进的重要抽样法在电力系统可靠性评估中的应用[J]. 电网技术, 2005, 29(13): 56-59.

SONG Xiaotong, TAN Zhenyu. Application of improved importance sampling method in power system reliability evaluation[J]. Power System Technology, 2005, 29(13): 56-59.

[22] The Reliability Test System Task Force of the Application of Probability Methods Subcommittee. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(6): 2047-2054.

[23] GRIGG C, WONG P, ALBRECHT P, et al. The IEEE reliability test system-1996. A report prepared by the reliability test system task force of the application of probability methods subcommittee[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1010-1020.

(编辑 魏小丽)

Reliability evaluation based on modified mixed sampling and minimum load-cutting method

SUN Tengfei1, CHENG Haozhong1, ZHANG Libo1, ZHOU Qinyong2, HE Hailei2, ZENG Pingliang2

(1. Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education (Shanghai Jiao Tong University), Shanghai 200240, China; 2. China Electric Power Research Institute, Beijing 100192, China)

As its sampling frequency is independent of the scale of the system and non-linear performance, Monte-Carlo simulation is widely applied to reliability evaluation of a complex large transmission system because of its accurate result. However, it takes a relatively long period of time to obtain a higher accurate reliability index. In order to solve this problem, the combination of importance sampling method and discrete Latin hypercube sampling method is able to reduce the variance of the sample space and uniformly sample it simultaneously, which improves the convergence of Monte-Carlo simulation. This paper points out that, the combination of sensitivity analysis and linear programming in the process of overload correction is able to guarantee the solution optimality as well as improve the solving speed. Finally, the algorithm is presented for IEEE RTS79, IEEE RTS96 and a certain system to obtain the reliability index, the result proves its practicability. This work is supported by National Natural Science Foundation of China (No. 51337005) and Fundamental and Prospective Science and Technology Project of State Grid Corporation of China (No. XT71-14-002).

modified Latin hypercube sampling; minimum load-cutting method; power system; reliability evaluation; Monte-Carlo simulation; sensitivity analysis

10.7667/PSPC151355

国家自然科学基金重点项目(51337005)；国家电网公司基础性前瞻性项目(XT71-14-002)

2015-08-04；

2015-11-22

孙腾飞(1990-)，男，通信作者，硕士研究生，主要研究方向为电力系统规划、电力系统可靠性；E-mail：soar1990@sina.com 程浩忠(1962-)，男，博士，教授，博士生导师，主要研究方向为电力系统规划、无功和电压稳定、电能质量等。