分区域Gamma预编码校正的相位误差补偿

林俊义，黄剑清，江开勇



分区域Gamma预编码校正的相位误差补偿

林俊义，黄剑清，江开勇

( 华侨大学a. 福建省特种能场制造重点实验室；b. 厦门市数字化视觉测量重点实验室，福建厦门 361021 )

针对现有结构光视觉测量中普通投影仪亮度不均匀引起系统Gamma非线性畸变值分布差异，从而导致相位误差问题，提出了一种自适应分区域Gamma预编码校正方法。首先，介绍了结构光双目视觉测量原理以及标准步相移法。接着，分析了投影仪和相机的Gamma非线性畸变对光栅正弦性的影响以及预编码校正方法。然后，在获取Gamma值分布规律的基础上，根据Gamma值的变化与相位误差的关系确定分区域阈值大小。最后，根据确定的阈值对测量视场进行区域划分，获取各区域Gamma值，并对标准白板和汽车挡泥板进行了实际测量。实验结果表明：本文方法比相同条件下采用单一Gamma值预编码校正方法在相位误差的补偿精度上提高了约30%，在三维数据的测量精度上提高了约15%。该方法能更好地减小相位误差，提高结构光视觉测量系统的精度。

结构光视觉测量；相移法；分区域Gamma预编码校正；相位误差补偿

0 引 言

结构光视觉测量方法具有精度高、速度快、非接触等优点，得到了广泛的关注与应用。该方法通过相机采集投射于物体表面的正弦光栅图像，采用相移法计算相位主值，通过相位展开获得全场唯一的绝对相位值，并基于相位信息进行三维重建[1-2]，由此可见，相位的提取精度直接影响到系统最终的测量精度。而影响相位提取精度的因素有相移偏差、投影仪和相机的非线性畸变、外界环境光、量化误差和系统振动等。其中最主要是投影仪和CCD相机的非线性畸变，即Gamma畸变。畸变导致采集到的光栅图像非正弦化，引起相位值计算误差，从而降低了系统的测量精度[3]。国内外学者提出了众多减小或消除该误差的方法，主要可以归为两类：相位误差补偿法和Gamma预编码校正补偿法。其中Gamma预编码校正方法只需进行一次校正，后续测量过程无额外的补偿计算，具有速度快、计算简单等特点。如Thang等提出了一种基于Gamma预编码的校正方法，该方法通过假定两个Gamma值来求取方程组的求解参数，再对方程组进行求解得到最终用于预编码的Gamma值[4]。ZHANG等进一步推导了连续相邻的三个谐波系数与Gamma值之间的递推关系，并采用离散傅里叶变换对周期性的采样信号进行处理获得谐波系数，然后根据递推公式计算出Gamma值，并采用该单一的Gamma进行预编码校正[5]。Xiao等提出采用单张正交光栅条纹图进行傅里叶变化获得系统Gamma值的方法[6]。Zheng等提出了一种两步相移法来求取预编码值的方法，精度能与7步相移法相媲美[7]。Zhou等研究了环境光对预编码方法补偿相位误差的影响[8]。

然而，现有的Gamma预编码补偿法均采用整体单一预编码校正的方法，在假设测量范围内获得的每个像素点的Gamma值是相同的前提下，采用Gamma值均值进行预编码校正。而实际测量系统中，普通投影仪的亮度并不均匀，一般亮度均匀度为85%，因此相机获取的图像亮度也不均匀，造成不同像素位置计算获取的Gamma值并不相同，而且测量视场越大，亮度不均匀越明显，Gamma值差异越大。直接采用整体校正的方法存在较大的相位误差，本文提出一种自适应分区域的Gamma预编码校正法，以解决相位误差问题，提高系统的测量精度。

1 原 理

1.1 结构光双目视觉测量原理

结构光双目视觉测量系统由一台投影仪、两台CCD相机组成，当投影仪投射设定的光栅图像至被测物体表面时，相机同时采集变形后的光栅图像，对图像进行处理以获取相关相位信息，根据立体视觉原理即可求得被测物体表面三维数据。其中相位获取一般采用标准步相移法，具体过程如下[10-11]：

将计算机生成的具有一定相位差的幅正弦光栅图像投射到物体表面，其中第幅图像上任意一点的亮度值可以表示为

在同一个测量幅面内往往包含多个正弦相位周期，解相得到的相位主值并不具有全场唯一性，因此，还需要进行相位展开。本文采用格雷码编码辅助相位展开法。设定正弦相位周期与格雷码周期相同，使得每个正弦周期都对应唯一的格雷码值，而且相邻周期之间的格雷码值差值为1。可按式(3)进行相位展开，获得绝对相位值。

经过相位展开后，每个像素点的相位值具有全场唯一性，通过立体匹配可得到视差，再根据立体视觉原理即可获得目标测量点的三维坐标。

1.2 预编码校正方法

在实际测量系统中，投影仪和相机存在非线性Gamma畸变，导致通过相机获取的光栅图像与理想的正弦光栅图像存在差别，这将引起上述计算出来的相位存在误差[12]。分析Gamma畸变导致相机获取调制光栅图像呈非正弦性的过程如下：

面的调制后可以表示为

1.3 系统Gamma值分布规律

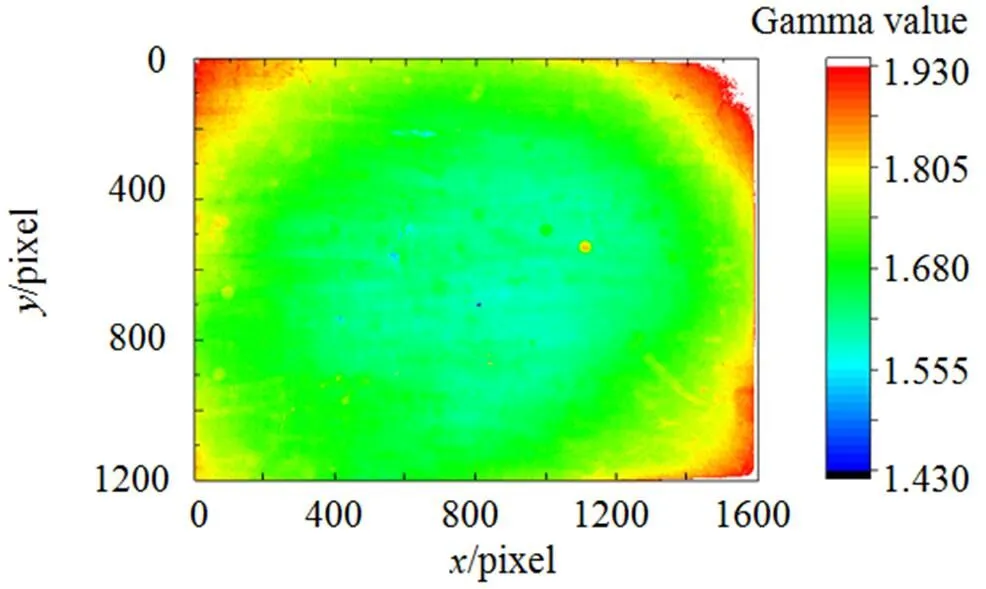
图1 左相机Gamma值分布图

1.4 自适应分区域Gamma预编码校正

Gamma值在测量范围内分布并不均匀，虽然可以对每个像素点进行校正，但计算量非常大，因此提出分区域Gamma值预编码校正的方法。该方法既需要保证相位补偿精度，又得使区域数目较少。根据文献[12]的研究结论可以推导出如下关系：

一般而言，在投影中心处Gamma畸变程度是最低的，因此，在投影中心处一定范围内寻找Gamma最小值，再以此Gamma最小值加上为限制，划出第一个区域，以此类推可以划分各个区域。以Gamma最小值为中心，将幅面划分为四个象限，下面以第一象限为例，具体阐述该方法的步骤。假设该幅面的第一象限区域被个同心圆划分如图2所示，其中。

图2 第一象限划分区域示意图

1) 调整硬件设备，使得投影中心在测量视场中心附近，并在投影中心附近搜索出Gamma矩阵的最小值，以该最小值的位置作为区域划分中心，并根据要求的测量精度确定出Gamma值的最大变化量；

3) 对各区域图像采用该区域Gamma均值进行预编码校正。

2 实验结果及分析

本文测量系统主要由一台投影仪，一对CCD相机和焦距为16 mm的Computar镜头组成，投影仪的型号为明基W5500，分辨率1 600 pixel´1 200 pixel；相机型号为IMAGING SOURCE，分辨率为1 600 pixel´1 200 pixel。测量的距离为1 600 mm，单次测量范围为800 mm×600 mm，测量系统的结构如图3所示。

首先对测量范围内各个像素点的Gamma值进行标定。由计算机生成一系列灰度值范围在[0,255]的灰度图像。灰度图像之间的灰度值增量为5个灰阶，并投影至标准白板上。左相机采集后利用式(7)对投影幅面内的Gamma值进行标定，从而获得整个幅面任意像素点的Gamma值。任意取左相机中间区域某一个像素点，其灰度响应曲线如图4所示，图中红色实线表示实际测量结果，绿色虚线表示理想的响应曲线。为了能够获得准确的Gamma值，本文标定过程中将剔除弱响应和过响应两个区域，即计算机只生成一系列灰度值范围在[60，230]的灰度图像。

图3 结构光视觉测量系统

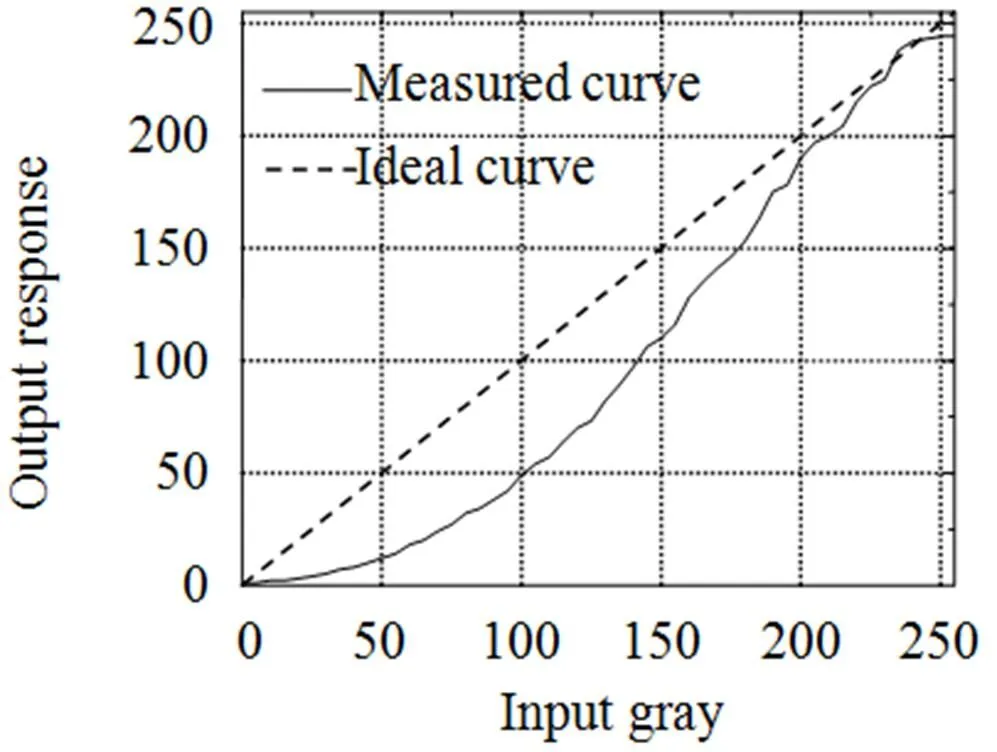
图4 灰度响应曲线

系统标定所得到左相机(系统)Gamma值的静态统计结果如图5所示。其中Gamma最大值为1.83，最小值1.31，均值为1.49，标准差为0.075；同样可以得到右相机(系统)的Gamma值情况。显然Gamma值在投影幅面上的分布是不均匀的。左相机整个测量视场内的Gamma值分布以图像的形式显示如图1所示，可以看出Gamma值的分布呈近似圆环的空间分布规律。

为了验证本文方法的有效性，采用25步相移法计算理想相位值，三步相移法完成实际测量。分别采用无任何补偿、整体单一的Gamma值预编码补偿和分区域Gamma值预编码补偿的方法对标准白板进行测量。其中，整体单一的Gamma值预编码补偿法中，预编码值采用Gamma矩阵的平均值。分区域Gamma值预编码补偿法中，阈值的确定如下：

以不同的Gamma值，获取测量区域相位误差均值，拟合相位误差与Gamma值的曲线，得：

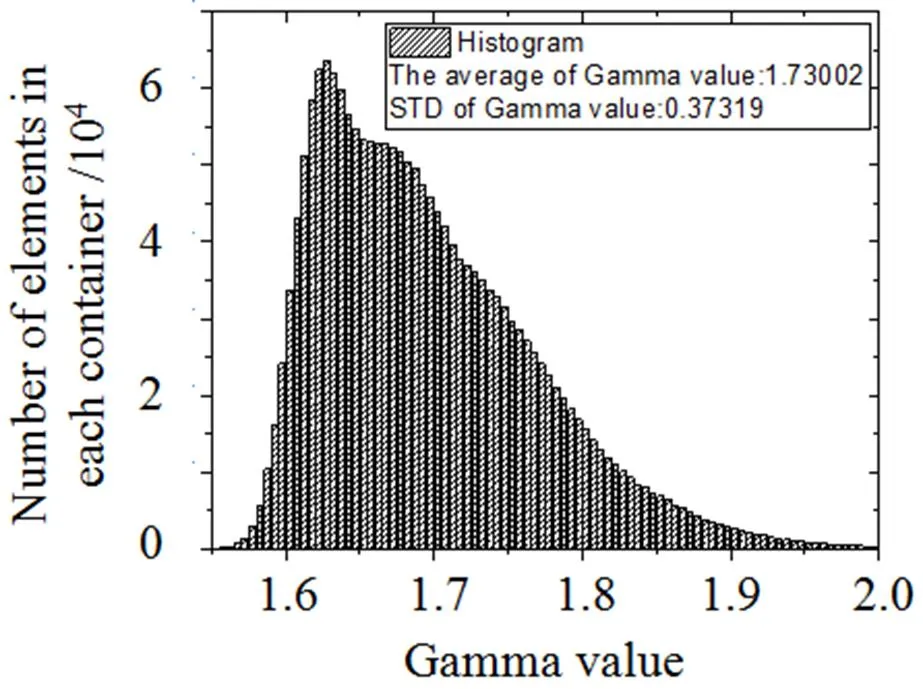
图5 Gamma值静态统计分布直方图

采用无任何补偿以及不同的补偿方法对标准白板进行测量。图6所示为测量所用的光栅，分别为(a)计算机生成的原始光栅、(b)无任何补偿采集的光栅、(c)单一预编码值补偿采集的光栅和(d)分区域预编码补偿后采集的光栅。图7是与之对应的光栅条纹第600行像素的横截面图。

图6 不同方法预编码后相机采集的光栅条纹图像

图7中可以看出，整体单一预编码的光栅条纹相比没有补偿的光栅条纹有更高的亮度值，但是整体振幅范围缩小，测量时对噪声比较敏感；而且整体单一预编码补偿的前后都没有改变光栅分布的均匀性，光栅中间亮度会比两端稍高，因此采用该方法补偿后，在相位计算时容易导致中间和周围的相位补偿存在残余误差。蓝色(单点画线)的截面线是采用本文方法补偿的，可以看出其振幅与理想光栅基本相近，而且光栅的中间与两端的均匀性也得到很好的改善。光栅解相后，相位取左相机测得的第600行的绝对相位误差进行分析，结果如图8(a)、(b)所示。绿色(短画线)曲线是没有进行预编码补偿的光栅，解相后存在着较为明显而且均匀的相位波动，蓝色(单点画线)曲线是采用整体单一预编码补偿的，其相位波动较为不明显，但相比红色(双点画线)曲线的分区域预编码补偿法，该方法仍然有一定的相位误差。由于左右相机的Gamma值分布也不同，本实验采用单步投影法和两步投影法分别进行测量比较，其中单步投影法是以左相机参数结合本文的方法进行预编码校正，而两步投影法为左右相机各自预编码校正，图9表示不同的方法与理想光栅之间的相位误差。显然两步投影法补偿与本文方法相结合后测量的效果会较好，后续测量采用两步投影法。对比了整体的单一Gamma值预编码校正方法与本文方法的相位标准偏差与最大误差，根据式(14)计算标准差的相对误差：

其中：表示没有补偿的相位误差的标准差，表示所使用的补偿方法得到的相位误差的标准差，计算结果参见表1，可以看出本文方法能将相位误差降低约30%。

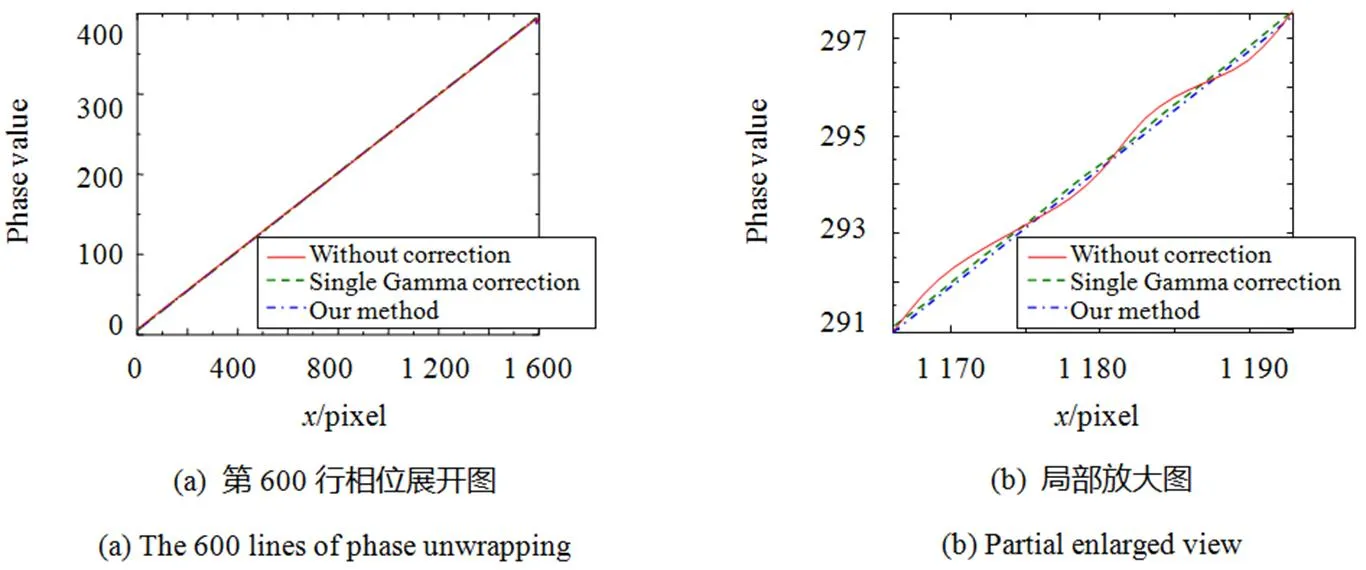
图8 不同预编码补偿方法的相位展开图

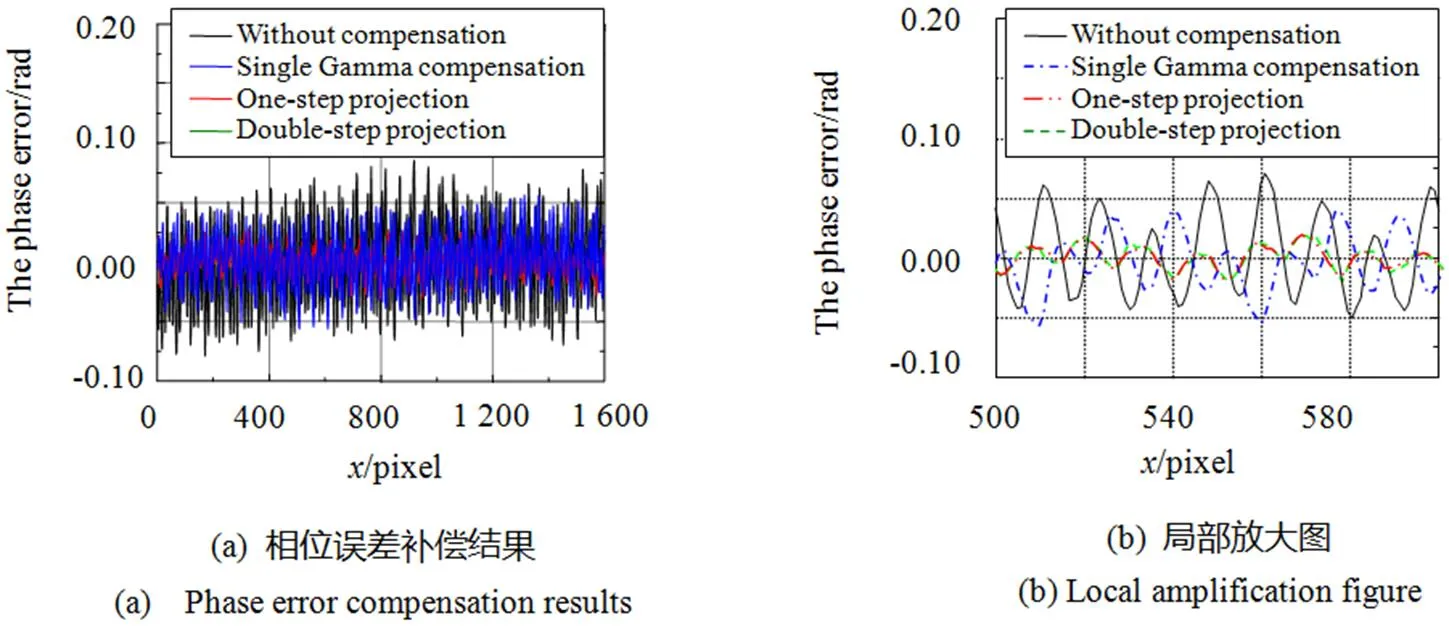
图9 不同方法的相位误差补偿结果

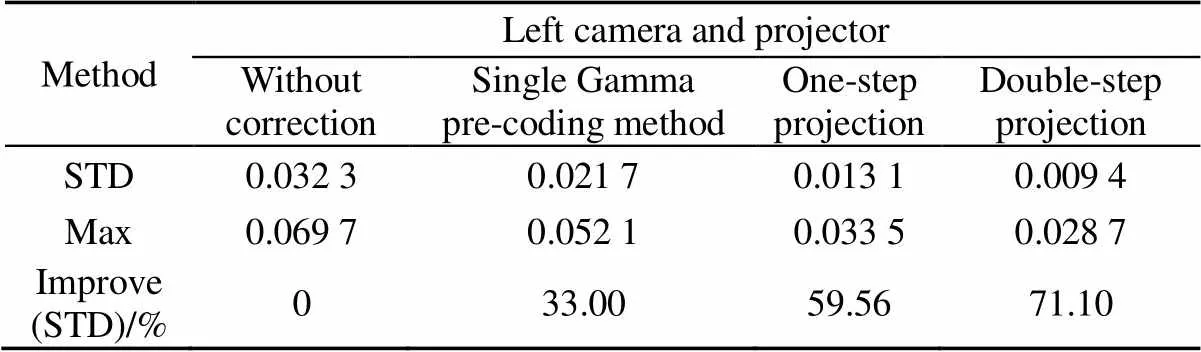
表1 两种方法对相位误差的补偿效果

图10是标准白色平板三维数据测量结果与最佳拟合平面的对比图，图10(a)~10(c)分别是无任何补偿测量的三维数据、采用整体单一预编码值补偿的三维数据和本文提出的方法测量得到的三维数据。显然，没有补偿的三维数据表面存在明显的水波纹；整体的单一预编码值补偿后水波纹能够得到抑制，但是不够明显；而采用本文提出的方法能够明显的抑制水波纹，获得更好的测量表面。表2比较了测量的标准平面与最佳拟合平面之间的最大距离、平均距离和标准偏差。根据式(14)计算，本文提出的方法所计算得到的标准差相比整体单一预编码补偿法，其标准偏差的相对误差降低了约15%左右。实验表明，本文的方法在一定程度上能够提高测量系统的最终测量精度。

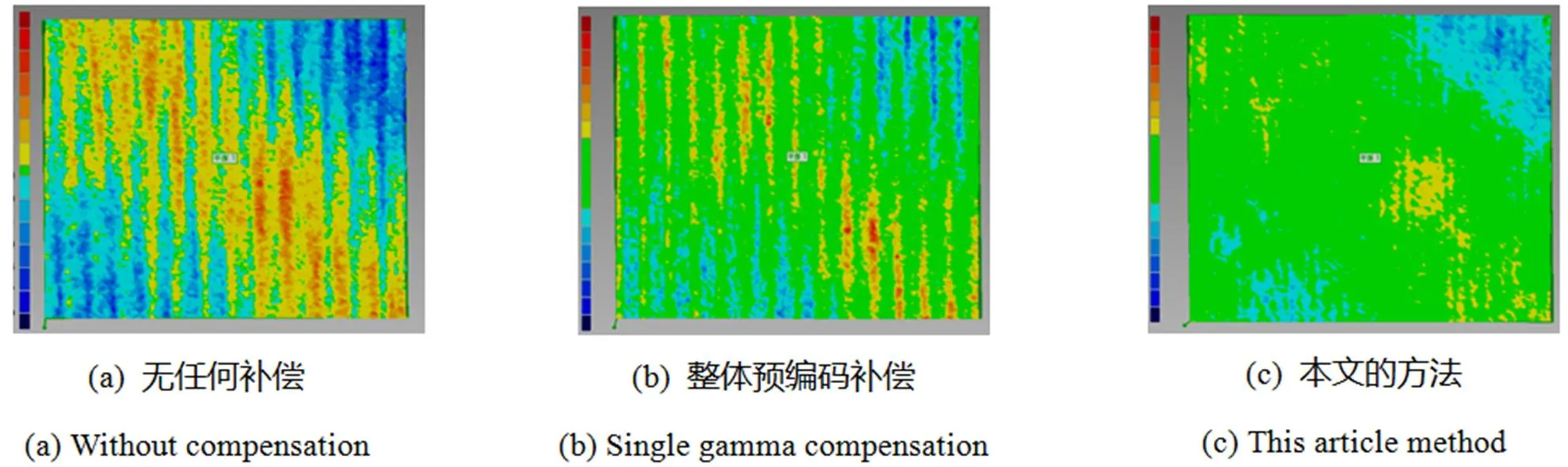
图10 标准白板测量后与最佳拟合平面比较

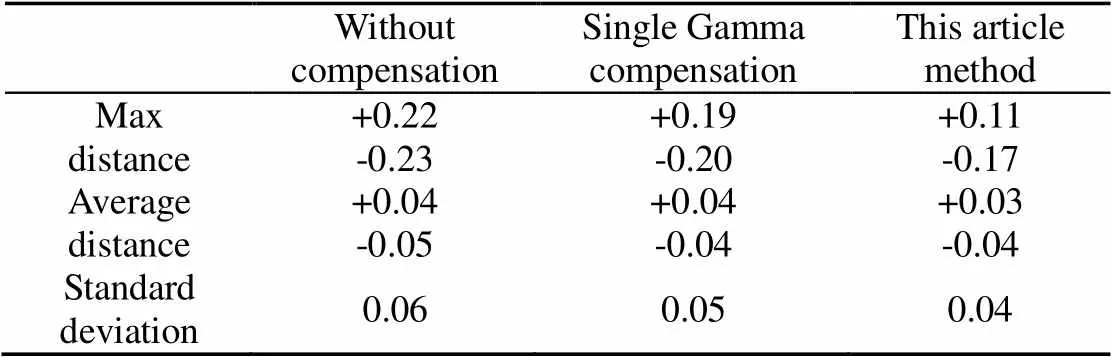
表2 标准白板与最佳拟合平面比较结果

3 结 论

本文针对结构光视觉测量中，普通投影仪亮度不均匀引起系统Gamma非线性畸变值分布差异，从而导致相位误差问题，提出了分区域Gamma预编码校正的补偿方法，分析了Gamma值对相位误差的影响，研究了Gamma值的分布规律以及与相位误差的关系，确定了分区域的阈值并对各区域进行了预编码校正，最后对两种方法的绝对相位误差补偿效果以及实际测量数据进行了比较。实验结果证明：本文提出的方法比整体校正补偿方法在相位精度上提高约30%左右，在三维数据的测量精度提高约15%。

参考文献：

[1] 陈锋，苏显渝，向立群. 结构光投影测量中物体不连续处误差分析[J].光电工程，2011，38(7)：74-80.

CHEN Feng，SU Xianyu，XIANG Liqun. Analysis of Phase Error at Discontinuities in the Measurement Based on Structured Light Projection [J]. Opto-Electronic Engineering，2011，38(7)：74-80.

[2] 黄磊，苏显渝，向立群. 在PMP 中环境光强变化引入的误差与校正[J]. 光电工程，2006，33(9)：80-84.

HUANG Lei，SU Xianyu，XIANG Liqun. Error caused by non-constant environmental light and rectification in PMP [J]. Opto-Electronic Engineering，2006，33(9)：80-84.

[3] ZHOU Ping，LIU Xinran，ZHU Tongjing. Analysis of the relationship between fringe angle and three-dimensional profilometry system sensitivity [J]. Applied Optics(S0003-6935)，2014，53(13)：2929-2935.

[4] HOANG Thang，PAN Bing，DUNG Nguyen，. Generic gamma correction for accuracy enhancement in fringe-projection profilometry [J]. Optics Letters(S0146-9592)，2010，35(12)：1992-1994.

[5] ZHANG Xu，ZHU Limin，LI Youfu，. Generic nonsinusoidal fringe model and gamma calibration in phase measuring profilometry [J]. Journal of the Optical Society of America(S0146-9592)，2012，29(6)：1047-1058.

[6] 肖焱山，曹益平，武迎春，等. 基于傅里叶频谱分析的相位测量轮廓术系统Gamma非线性校正方法 [J]. 光学学报，2012，32(12)：1212004.

XIAO Yanshan，CAO Yiping，WU Yingchun，. Gamma Nonlinearity Correction Based on Fourier Spectrum Analysis for Phase Measuring Profilometry [J]. Acta Optica Sinica，2012，32(12)：1212004.

[7] ZHENG Dongliang，DA Feipeng. Gamma correction for two step phase shifting fringe projection profilometry [J]. Optik(S0030-4026)，2013，124：1392-1397.

[8] ZHOU Ping，LIU Xinran，HE Yi，. Phase error analysis and compensation considering ambient light for phase measuring profilometry [J]. Optic and Lasers in Engineering(S0143-8166)，2014，55：99-104.

[9] ZHANG Song，YAU Shing-Tung. Generic nonsinusoidal phase error correction for three-dimensional shape measurement using a digital video projector [J]. Applied Optics(S1004-924X)，2007，46(1)：36-43.

[10] MA Shengjia，QUAN Chenggen，ZHU Rihong，. Investigation of phase error correction for digital sinusoidal phase-shifting fringe projection profilometry [J]. Optics and Lasers in Engineering(S0143-8166)，2012，50(8)：1107-1118.

[11] LIU Kai，WANG Yongchang，QI Hao，. Gamma model and its analysis for phase measuring profilometry [J]. Journal of the Optical Society of America(S0146-9592)，2010，27(3)：553-562.

Subregional Gamma Pre-coding Correction for Phase Error Compensation

LIN Junyi，HUANG Jianqing，JIANG Kaiyong

( a. Fujian Provincial Key Laboratory of Special Energy Manufacturing; b. Xiamen Key Laboratory of Digital Vision Measurement Huaqiao University, Xiamen 361021, Fujian, China)

In structured light vision measurement, since non-uniformity of brightness of the common projector caused nonlinear distortion Gamma value distribution difference resulting in phase error problem, a self-adaptive subregional Gamma value pre-coding correction method was proposed. First, the principle of structured light stereo vision measurement and standardstep phase shifting method is introduced. Second, the projector and the camera's nonlinear distortion of sine grating and the Gamma value pre-coding correction method are analyzed. Then, on the basis of Gamma value distribution, according to the relationship between the change of Gamma value and the phase error, subregional threshold was calculated. Finally, according to the threshold, the measurement field was divided and subregional Gamma pre-coding correction method was implemented, and actual measurement was carried out on a standard white plate and a fender. Experimental results indicate, under the same conditions, compared with single Gamma pre-coding correction method, the proposed method can further improve phase error compensation about 30%, and the measurement accuracy increase by about 15% in the 3D data.

structured light vision measurement; phase-shifting method; subregional Gamma pre-coding correction; phase error compensation

1003-501X(2016)09-0032-07

TB92；P391

A

10.3969/j.issn.1003-501X.2016.09.006

2016-01-11；

2016-03-28

国家科技支撑计划项目(2015BAF24B01)；福建省科技计划重点项目(2008H0085)；福建省科技重大专项专题项目(2014HZ0004-3)

林俊义(1977-)，男(汉族)，福建莆田人。副教授，硕士，主要从事机器视觉方面的研究。E-mail: ljy2004@hqu.edu.cn。

黄剑清(1990-)，男(汉族)，福建南安人。硕士研究生，主要从事面结构光三维测量方面的研究。E-mail: hjqsuccess@163.com。