干预分析在肾综合出血热发病过程模拟中的应用

程幸福

（武汉大学数学与统计学院，湖北武汉430072）

干预分析在肾综合出血热发病过程模拟中的应用

程幸福

（武汉大学数学与统计学院，湖北武汉430072）

为探讨应用干预分析模型模拟肾综合出血热发病数的可行性，对武汉市蔡甸区1980～2009年的月度发病数据建立干预分析模型，并将模拟效果与单纯使用ARIMA模型的模拟效果进行对比，发现干预分析模型能够很好地拟合HFRS的月发病数，给疾病的预防和控制提供科学依据。

干预分析；ARIMA模型；肾综合征出血热

干预分析的研究始于威斯康辛大学统计系教授Box和Tiao于1975年联合发表《Intervention Analysis with Applications to Economic and Environ⁃mental Problems》，并迅速引起人们的关注，用于描述经济政策的变化及其给经济带来的影响。研究干预分析模型就是从定量分析的角度来评估政策干预或突发事件对经济过程的具体影响。

1　干预分析模型

1.1干预分析简介

时间序列常受到诸如节假日、罢工、促销和其他政策变化之类的外部事件的影响，这类外部事件称为干预。干预分析就是在时间序列建模中纳入干预信息的建模方法。

1.2常见的干预变量

为简单起见，考虑单一干预的简单情况，假设…，Yt-1，Yt，Yt+1，…是得到的时间序列，经过适当变换后，可表示为

式中：yt是由Yt经某个变换得到的；mt是均值函数的变化；Nt是某个自回归滑动平均求和过程，代表未受干预的时间序列所适合的模型，可能是平稳的也可能是非平稳的、季节的或非季节的。假设Nt可以表示为ARIMA（p，d，q）模型：

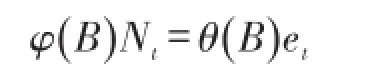
式中：B是向后推移算子，假设这个时间序列在T时刻受到某个干扰，即在时刻T之前，mt=0。

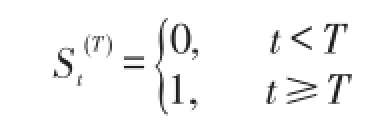
干预分析模型的建立基于干预变量的引入，通过若干参数来说明干预对均值函数的影响，例如阶梯函数函数：阶梯函数通常代表一种干预一旦发生将永久持续下去的情形。类似用脉冲函数作为干预发生时间的指示器，即Pt（T）是干预发生的标记：

1.3干预模型的表示

干预事件的影响多种多样，但几乎所有的影响都可以用以上2种干预变量的线性组合来表示：

1）如果干预导致了均值函数发生了即时且永久性的偏移，那么，偏移可以建模为

式中：ω表示干预导致均值未知且永久的变化。如果干预经过d个时间单位的延迟后作用才显现，并且d已知，那么可以设定：

2）如果干预只是逐渐地影响均值函数，其全部影响作用只有经历很长时间才能充分体现出来，这时可以用AR（1）模型来表示mt，其误差项由滞后1的St

T的倍数充任：

3）如果干预仅在t=T时刻产生影响，则令

4）如果干预影响逐渐消失，通过AR（1）类型的模型表示均值函数的变化：

如果均值的变化发生于d个时间单位的延迟之后，且该干预效应逐渐消失，则可规定：也可以用延迟算子B来表示上述模型，Bmt=mt-1且

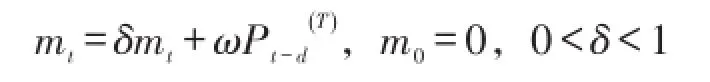
1.4异常值

异常值是一些不规则的观测值，其出现可能源自测量误差与复制误差其中之一，或者两者皆有，也可能是源于基础过程发生了突发的短期性变化。对于时间序列而言，可识别的异常值，即可加异常值与新息异常值，通常分别记为AO与IO。

1）可加异常值AO如果基础过程yt在时刻T时受到了可叠加性的扰动而得到yt，此时就会出现可加异常值，它们之间有下面的关系：

仅在T时刻有yT′=yT+ωA，其余情况下yt′=yt，即如果时间序列在T时刻存在一个可加异常值，意味着它只在时刻T受到影响。可加异常值也可被看作一种在时刻T上具有脉冲响应的干预，因此均值函数建模为

2）新息异常值IO如果处于时间T时的误差（也称为新息）受到了干扰（即误差变为et′=et+ωI，其中et是零均值白噪声）。因此仅在时刻T有eT′=eT+ωI，其余情况et′=et。假设无扰过程是平稳的，且可表示为一个MA（∞）过程：

则受到扰动的过程可以表示为

式中：ψ0=1且当 j＜0时有ψj=0。因此，一旦发生新息异常值，则新息异常值将从该异常值发生的时刻T起对之后所有的观测产生扰动。若Nt满足φ（B） Nt=θ（B） et，则在此情况下，模型可表示为

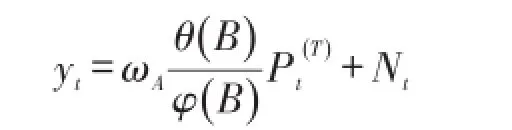
2　肾综合出血热发病过程的模拟

2.1数据来源

选择武汉市蔡甸区HFRS月发病数序列（已作开方处理）作为分析对象，记录了1980年1月～2009年12月的HFRS发病数共360个观测，如图1所示。

2.2对基础无扰过程建模

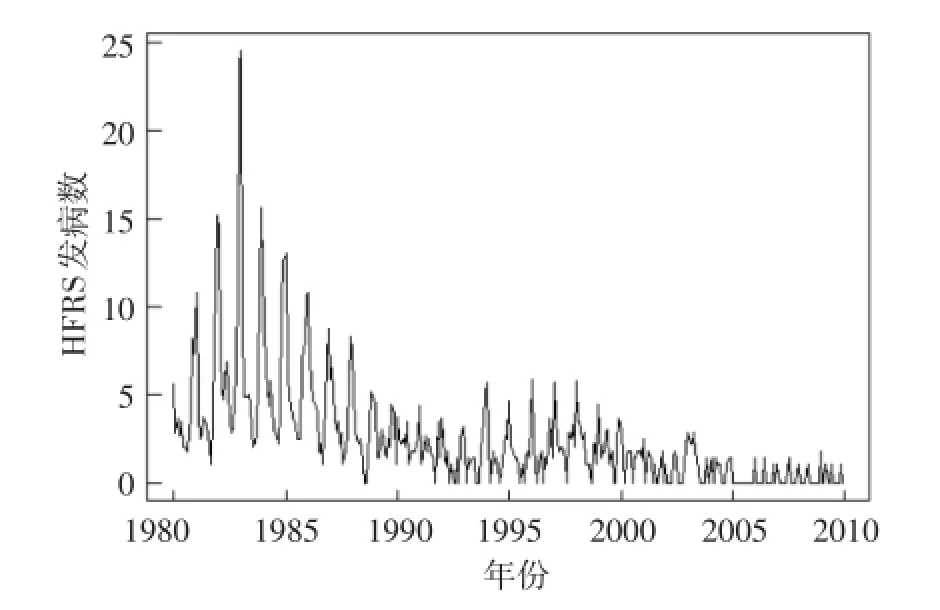
图1　HFRS序列图

从图1发现1982年12月（即第36个数据）迅速增长，可以认为在1982年12月有一个对HFRS发病数序列产生干扰的事件发生。在进行干扰分析之前，检查时间序列并且建立基础模型，为此选取干预发生之前的数据（即HFRS序列的前35个数据）进行建模。通过分析发现基础无扰过程可以用季模型ARIMA（0，1，1）×（0，1，1）12表示。即如果用Nt表示基础无扰过程，则有

2.3对干扰过程建模

在确定了基础无扰过程的模型后，模型的残差即干扰过程mt，通过对mt进行简单自相关分析发现起始于1982年12月份的干扰过程可以用一个AR（2）过程来描述，因此对干扰过程可以建模为

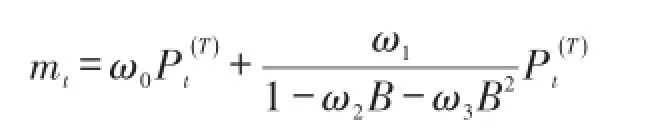
式中：T表示1982年12月。另外，模型诊断表明：在1981年2～3月有可加异常值，1981年12月、1987 年1月和1990年12月存在新息异常值。因此，最终确定的模型为

2.4参数估计

用极大似然估计法估计模型的参数，基础无扰过程Nt的参数估计结果如表1所示。由表1所示参数得到干预模型：它反映了干预事件对HFRS序列的影响。

2.5与ARIMA模型比较

为了考察干预分析模型的模拟效果，考虑与单纯的使用ARIMA模型对比，两模型的参数估计结果及检验结果见表2。由表2可见干预分析残差平方和与赤池信息量（AIC）都较小，且极大似然估计量也有所提高。因此选择干预分析模型比较合适。

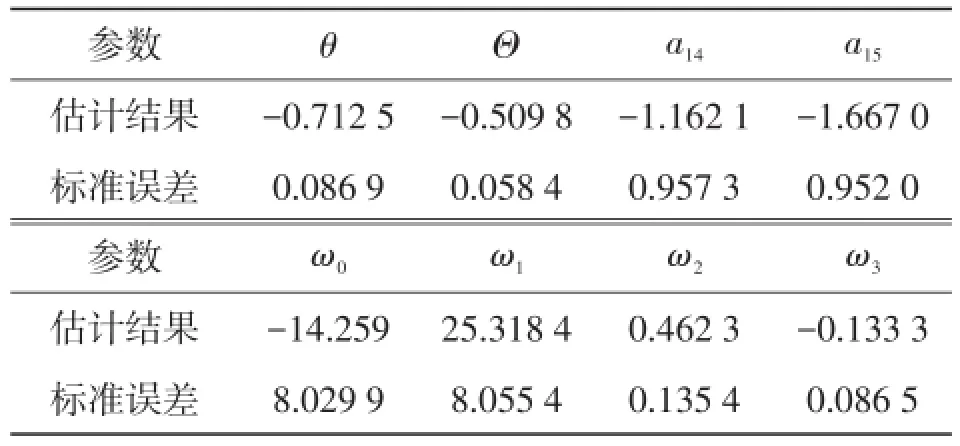
表1　参数估计结果

表2　干预分析模型与ARIMA模型比较

3　总结

利用带干预的ARIMA模型预测武汉蔡甸区肾综合征出血热月发病数的变化趋势时，由于考虑了干预的影响，预测结果一般要比传统ARIMA模型预测结果准确，当然也相对正确客观。本文中采用干预分析模型对肾综合征出血热月发病数发病趋势的变化进行建模，得到了较精确的模型，为武汉市蔡甸区肾综合征出血热的预防和防治提供了一定的理论依据。

［1］冯文权，蔡基栋.干预分析及其应用［J］.武汉大学学报，1994（6）：1-7.

［2］G E P Box，G C Tiao.Intervention Analysis with Applica⁃tions to Economic and Environmental Problems［J］.Jour⁃nal of the American Statistical Association，1975，70 （349）：70-79.

［3］George E P Box，Gwilym M Jenkins，Gregory C Reinsel. Time Series Analysis Forecasting and Control［M］.3版.北京：人民邮电出版社，2005：462-471.

［4］Jonathan D.Cryer，Kung-Sik Chan.时间序列分析及应用［M］.潘红宇，译.2版.北京：机械工业出版社，2011.

［5］马亮亮，田富鹏.ARIMA模型在胆结石病发病率预测中的应用［J］.军事医学，2010（5）：469-472.

［6］孙玉环.ARIMA模型在测算重大突发事件影响中的应用［J］.统计与决策，2006（14）：24-26.

Application of Intervention Analysis in Simulation of Hemorrhagic Fever with Renal Syndrome

Cheng Xingfu
（School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

The intervention analysis model was established based on the monthly incidence data of Caid⁃ian District of Wuhan from 2009 to 1980 in order to simulate the feasibility of comprehensive kidney hemorrhagic fever incidence.And the simulation results were compared with the simulation results of the ARIMA model.It is found that the intervention analysis model can fit well the monthly incidence of HFRS.And this result provides scientific basis for the prevention and control of diseases.

intervention analysis；ARIMA model；HFRS

O212.1

A

1008-5483（2016）02-0074-03

10.3969/j.issn.1008-5483.2016.02.017

2016-04-27

程幸福（1990-），男，安徽涡阳人，硕士生，从事随机分析方面的研究。E-mail：1318247907@qq.com