基于储存应力折算的火工品恒加试验数据处理方法

王耀冬，俞卫博，宣兆龙，王绍山



基于储存应力折算的火工品恒加试验数据处理方法

王耀冬，俞卫博，宣兆龙，王绍山

（军械工程学院，河北 石家庄，050003）

在火工品储存可靠性评估中，针对恒加试验一般数据处理方法忽略火工品并非新品的问题，提出了基于储存应力折算的数据处理方法。通过等效和叠加，将储存应力下的储存时间折算为恒加试验各应力水平下的试验时间，并以此进行参数的极大似然估计。实例分析表明，该方法在评估储存应力和储存时间已知的火工品储存可靠性时，具有更高的准确性。

火工品；恒加试验；储存历史；时间折算；可靠性

恒定应力加速寿命试验（以下简称恒加试验）是火工品储存可靠性评估普遍采用的方法，具有操作简单、数据处理方法相对成熟等特点[1]。常用的数据处理方法有极大似然估计、近似无偏估计等，这些方法只注重试验数据而忽略了现场数据，即默认了试验样品皆为新品[2]。但实际工作中，为有效缩短试验周期，或在估计火工品剩余寿命的场合，常采用具有储存历史的火工品作为试验样品。如按上述方法进行处理，将忽略样品的储存环境应力和储存时间等重要现场数据，造成可靠性估计比实际偏大的问题。针对这一问题，本文提出了一种基于储存应力折算的数据处理方法，即把火工品在实际环境下的储存时间折算到恒加试验不同应力水平下的时间，再分别将各折算后的时间与各应力水平下的试验时间之和作为恒加试验中各应力水平下的最终试验时间，以此进行火工品的储存可靠性估计。

1 基于储存应力折算的数据处理方法

由于火工品在储存过程中采取了防止水分侵蚀的措施，因此，可简化为以温度为单因素的储存问题[3]。将实际储存温度应力水平S下储存时间t后的火工品，投入采用定时截尾的恒加试验中。设恒加试验的个应力水平为S(=1,2,……,)，对应投入的样本量为n，到达截尾时间t时的失效数为r。火工品的累积失效时间分布函数为()，则实际储存应力水平S下对应的累积失效函数为F()，试验应力水平S下对应的累积失效函数为F()。

1.1 基本假设

（1）温度应力水平下，适合火工品储存寿命的失效分布主要为Weibull分布[4]，即：

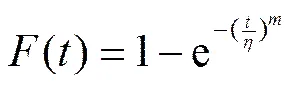
式（1）中：为时间；为形状参数；为特征寿命。

（2）不同温度应力水平S下，火工品的失效机理一致，即寿命分布中的形状参数保持不变[5]。

（3）火工品的特征寿命与温度应力水平之间的关系可用阿伦尼乌斯方程表示[6]，即：

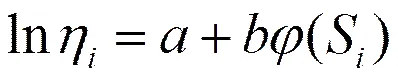
（4）根据Nelson累积失效原理[7]，火工品的剩余储存寿命仅依赖于当时已累积的失效部分和当时的应力水平，而与累积方式无关。

1.2 时间折算

将具有储存历史的火工品作为样品投入恒加试验，且储存历史已知时，必须充分考虑储存历史中环境应力、储存时间对试验样品失效的累积效应。由假设（4），在实际应力水平S下存储t时间的累积失效概率相当于在试验应力水平S下存储t时间的累积失效概率，其等效关系如图1所示。

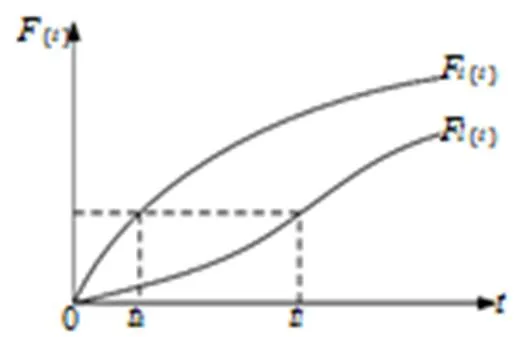
图1 等效关系

代入式（3）并化简得时间折算公式为：

则在应力S下的最终试验时间为：

式（6）中：t为应力S下的试验截尾时间，τ为应力S折算到应力S下的折算时间。

设在应力S下火工品的失效数为r，则此时的最终失效时间为：

式（7）中：t为应力S下失效数的失效时间；τ为应力S折算到应力S下的折算时间。

如恒加试验得到应力S下具有储存历史的样品失效时间分别是：

（8）

本试验采用黑龙江农垦总局八五七农场科技园的空育131等13种水稻品种，各品种均为移栽，田地条件、施肥量、田间管理等基本相似。种植时间为2010年5月15日-5月17日。由于当年高温，所有的水稻的主茎叶都比正常时的水稻少1片叶。各品种的名称及水稻叶片数如表1所示。

则用上述公式即可得到折算后样品的失效时间分别是：

具体模型如图2所示。

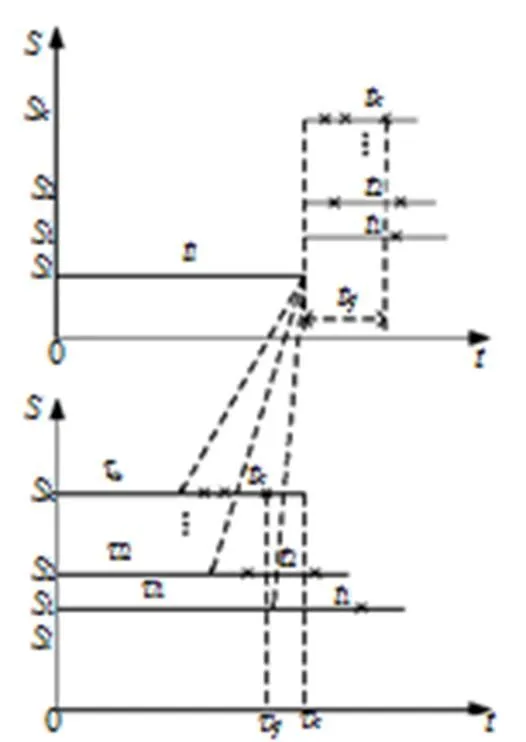
图2 基于储存应力折算的数据处理方法模型

1.3 参数估计

在前3个假设下，利用试验所得失效数据以及折算后的试验时间，对共同的值和加速方程中的,进行极大似然估计[8]，并求实际应力水平S下火工品的各种可靠性特征估计。

1.3.1 参数的极大似然估计

由式（4）可得：

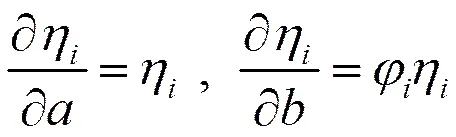
则，，极大似然估计的似然函数为：

对数似然函数为：

似然方程组为：

将式（4）代入似然方程组并利用迭代法编制C语言程序[9]，解此方程组即可得到参数，，的极大似然估计，，。

由加速方程求出在正常应力水平S下特征寿命η的极大似然估计为：

1.3.2 可靠性指标估计

基于和η的估计，即可得到火工品在正常应力水平S下储存t时间后的各种可靠性特征估计：

2 比较标准与实例分析

2.1 比较标准

在加速寿命试验中存在以下情况：（1）当样品为新品时，可能由于装配、运输等原因造成样品失效；或是样品非新品时，在储存期间已经失效。而在加速寿命试验前期对样品进行抽样检测时没有检测出失效就投入试验。（2）在加速寿命试验过程中，无论选取定时截尾或是定数截尾，当检测出样品失效时，该样品很可能已经失效一段时间，而记录的失效时间仍然是检测时间。由此可以认为，加速寿命试验无论采用何种数据处理方法，求得的可靠性估计都较实际偏大。因此，比较数据处理方法的优越性，就在于比较所得可靠性估计的大小，越小则越贴近于实际，该方法的准确性越高。

2.2 实例分析

某火工品已在正常温度下储存8a，对其进行定时截尾恒定应力加速寿命试验，已知其寿命分布为Weibull分布，以温度作为加速应力，取4个温度应力水平，每个应力下取25个样品，求该火工品在正常储存温度25℃下的可靠性指标。每个温度应力水平下的截尾时间和失效个数如表1所示，具体失效时间见文献[11]。

表1 截尾时间和失效个数

利用本文提出的方法进行求解，得到：

则火工品储存8a后的可靠度为：

用一般数据处理方法求得的可靠度为0.996 6，对比可以看出，利用本文提出的方法算得的火工品可靠度要小于一般方法所得的可靠度。

3 结论

实例分析对比表明，本文提出的基于储存应力折算的恒加试验数据处理方法评估火工品储存可靠性，较一般数据处理方法准确性更高，更贴近火工品实际储存可靠性变化。弥补了恒加试验一般数据处理方法评估具有储存历史的火工品可靠性时，忽略样品储存环境应力、储存时间等重要信息的不足。

[1] 李明伦,李东阳,郑波.弹药储存可靠性[M].北京:国防工业出版社,1997.

[2] 谭源源,张春华,陈循,等.基于加速寿命试验的剩余寿命评估方法[J].机械工程学报,2010,46(2):150-154.

[3] GJB736.8-90 火工品试验方法71℃试验法[S].国防科学技术工业委员会,1990.

[4] 徐振相,秦士嘉.火工品可靠性技术[M].北京:兵器工业出版社,1996.

[5] 郑波,杨宝强,南彬,等.步进应力加速寿命试验在预测底火贮存寿命中的应用[J].火工品,2003(1):19-21.

[6] 王凯民.火工品工程[M].北京:国防工业出版社,2014.

[7] 张春华.步降应力加速寿命试验的理论和方法[D].长沙:国防科学技术大学,2003.

[8] MAO Shi-song, HAN Qing. Statistical analysis of life and accelerated life test on weibull distribution case under typeⅠcensoring[J]. Application Probability Statistics,1991,7(1):61-97.

[9] 陈挚.用步进应力加速寿命试验法分析爆炸螺栓的可靠性[J].数学理论与应用,2001(2):106-110.

[10] 中国电子技术标准化研究所.可靠性试验用表[M].北京:国防工业出版社,1987.

[11] 茆诗松,汤银才,王玲玲.可靠性统计[M].北京：高等教育出版社,2008.

Data Processing Method Based on Equivalent Storage Stress for Constant Stress Accelerated Life Test of Initiating Explosive Device

WANG Yao-dong, YU Wei-bo, XUAN Zhao-long, WANG Shao-shan

(Ordnance Engineering College, Shijiazhuang, 050003)

In reliability assessment of initiating explosive device storage, aimed at the problem of general data processing method of constant stress accelerated life test, which ignore the initiating explosive device is not new, the data processing method based on equivalent storage stress was put forward. The methods convert the storage time to test time under each stress of constant stress accelerated life test by equivalent and superposition. Then, the maximum likelihood estimation of parameters were estimated according to the final test time. An analysis and comparison shows that, this method has higher accuracy to estimate storage reliability of initiating explosive device, which has been stored under certain stress and time.

Initiating explosive device; Constant stress accelerated life test; Storage history; Time conversion；Reliability

1003-1480（2016）02-0033-04

TJ450.2

A

2015-12-29

王耀冬（1991 -），男，在读硕士研究生，从事弹药保障与安全技术研究。