弹翼展开燃气作动筒内弹道预估技术

杨敏鹏，杨树彬，屠小昌，梁 宏，石权利，陈 静



弹翼展开燃气作动筒内弹道预估技术

杨敏鹏，杨树彬，屠小昌，梁 宏，石权利，陈 静

（陕西应用物理化学研究所，陕西 西安，710061）

为了有效控制弹翼展开过程，针对燃气作动筒的内弹道工作现象和过程进行了研究。以经典内弹道模型为基础，基于matlab 软件编制计算程序，完成弹翼展开过程燃气作动筒的数值仿真；通过与试验结果进行对比，验证了所建模型的合理性，从而为现有燃气作动筒的结构设计提供理论指导依据。

燃气作动筒；内弹道；状态方程；数值仿真

燃气作动筒作为一种动力驱动装置，具有输入能量小、作用速度快、可靠性高等优点，可以用来完成各种机构的展开和载荷释放，在工程实践中得到了广泛应用。本研究以内置锁紧式燃气作动筒内弹道为研究对象，对其进行仿真模拟，以节约实验成本。同时，该研究可以从原理上分析作动筒内弹道作用过程，对实验结果进行较为准确的预测，以指导实验的设计和实施[1]。

1 燃气作动筒结构及工作原理

传统折叠翼的设计多为在地面将弹翼折叠锁定，导弹发射升空后在空中将其解锁，展开定位，以确保弹翼在贮运时不受外界力学环境条件干扰，弹翼在旋转到位后位置状态保持相对不变，保证导弹正常飞行状态。为此需要设计一套专门的锁紧机构，但这样增加了弹体的尺寸，而且解锁过程也需附加动力完成，方式复杂，系统可靠性不高。为了解决导弹舱体体积小，弹翼重量指标要求严格等问题，本文将锁紧问题转化到作动筒的结构设计中，提出了一种内置分离螺母紧锁形式的作动筒设计技术，实现大的紧锁力，小的解锁力的特殊功能[2]。利用作动筒内装药燃烧后产生的燃气压强作用活塞推动折叠弹翼旋转展开。

内置分离螺母锁紧式燃气作动筒主要由筒体、基体、活塞、分离螺母、后盖、装药组件、点火器、缓冲垫块等零件组成。作动筒工作过程为：在平常不工作时，通过分瓣螺母的固定约束方式对活塞大的环境承载力进行锁定；一旦需要折叠弹翼展开，给出点火指令引燃装药并产生燃气压强，燃气压强作用到限位筒体端面产生推力剪断剪切销，限位筒体沿滑动配合面滑动，滑动超过一定行程后，分瓣螺母解除径向及周向约束，使分瓣螺母张开，完成解锁功能；燃气压强继续作用活塞，使活塞启动回缩运动，拉动折叠弹翼实现顺利展开功能。

2 燃气作动筒内弹道数学模型的建立

作动筒的作用原理与枪炮的作用原理基本一致，为使结果的处理和计算较为方便，采用经典内弹道模型，做如下假设：燃气作动筒活塞杆的运动符合牛顿定律；作动筒内主装药做平行层燃烧，且燃温为推进剂绝热燃烧温度；作动筒腔内燃气和空气均视为理想气体，燃气为热力学平衡状态；作动筒后腔内的空气为绝热压缩过程；忽略燃气的运动。

2.1 主装药选择与分析

按照计算与总体要求，设计工作时间180ms＜＜300ms，燃烧时间呈短时工作特性，因此装药设计应首选中高燃速发射药或推进剂，结合燃面设计，以达到质量流率设计要求。可选择的有：改铝铅-2、改铝铅-3、双钴-2、三芳-2发射药等。改铝铅-2、改铝铅-3推进剂燃温及燃速偏高，不利于热防护设计且装药肉厚较大，导致产品外径尺寸增加过多，故方案设计时不选用；三芳-2发射药属于三基类发射药，药型尺寸不易调节，故方案设计时也不选用。综合比较后初步考虑采用双钴-2。

本课题采用增燃面燃烧火药，燃面不再是常量，因推进剂燃面遵循平行层燃烧规律，将燃烧过程分成许多小区间，则每一小区间的燃面可看做常量。燃面计算模型见图1。

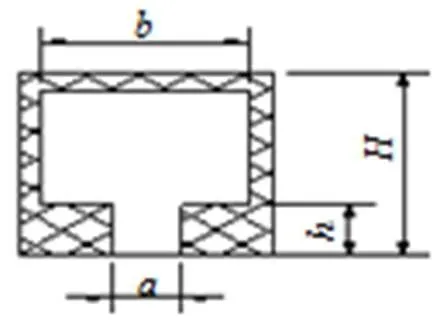
图1 燃面计算模型

其中：

2.2 燃速方程

根据燃气作动筒常用的压力范围，采用指数燃速定律，故燃速方程为：

式（2）中：为燃速系数；为压力指数；为作动筒内燃气压力。

2.3 燃气生成速率

由条件假设，火药燃烧符合几何燃烧定律，可知燃气生成速率为：

（3）

式（3）中：为单位时间内火药燃去的质量；为火药的密度；为燃烧表面积；为燃烧速度。将随肉厚变化的变燃面公式（1）和燃速方程（2）代入式（3）可求出火药已燃部分质量。

2.4 气体状态方程

为了简化计算，按理想气体考虑[3]，则状态方程为：

=0（4）

为修正实用时存在的误差，通过引入一个通常小于1的系数1予以修正，即修正后的定压燃烧温度为10。1可认为是常数，一般约在0.65左右。将式（3）代入式（4）可求得不同时刻对应的燃烧腔压强曲线。

2.5 活塞直线运动过程方程

在作动筒内弹道计算中，假设筒体内各点处压力相同，仅是时间的函数。作动筒活塞的受力情况见图2。燃气作动筒工作时, 运动部件活塞主要受5个力的作用，推力1由燃气压强1产生，后段筒体空气压缩制动阻力2，活塞杆密封圈与筒壁间摩擦力3、4，以及活塞对外输出弹翼载荷的反作用力[3]。根据受力模型分析：

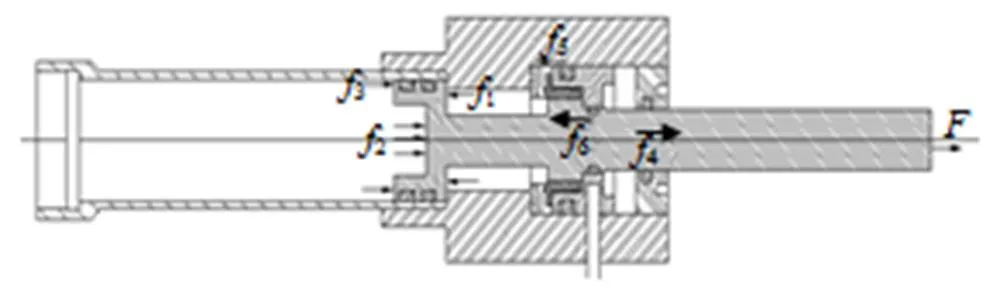
图2 活塞受力示意图

活塞的运动方程为：

式（5）中：为次要功系数；为活塞面积；为活塞质量；1为燃气作动筒燃烧腔内任一时刻的平均压力。设定作动筒后段筒体内的空气为理想气体，假定活塞运动，工作腔压缩空气的过程为绝热压缩[4]，固有绝热过程的过程方程式，得：

式（6）中：2为活塞不同行程位置时的作动筒后段筒体内空气压强；P为作动筒后段筒体内活塞初始行程位置=0时的空气压强，认为大气压强：P=1.013×105Pa；为空气的绝热指数，取=1.4。

由于活塞做直线运动，活塞加速度与行程关系式为：

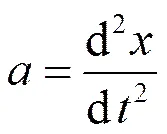
式（7）中：为活塞加速度；为活塞行程；为活塞运动时间。活塞与弹翼之间通过耳片连接，弹翼展开运动简图见图3。

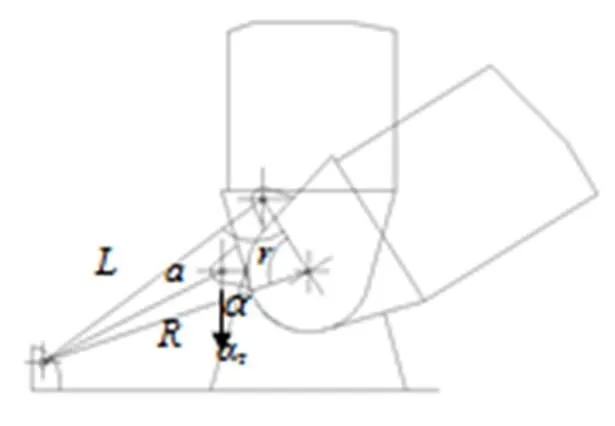
图3 弹翼展开运动简图

根据弹翼的运动规律，对运动机构受力分析，根据动量矩定理，可得弹翼的转动方程：

弹翼展开过程中的阻力矩包括弹翼展开时的气动升力引起的弹翼与轴承接触面圆环间的摩擦阻力矩和弹翼展开过程中锁紧弹簧销产生的摩擦阻力矩[5]，则有方程：

式（10）中：R为当量摩擦半径；为弹翼与接触面摩擦圆环间的摩擦系数；2为弹簧销对弹翼的摩擦阻力；2为摩擦阻力臂。

联立式（5）~（10）可得：

此即压强1、2随位移变化所要用的微分方程。

由简图3可知活塞杆与旋转半径的夹角是运动位移的函数：

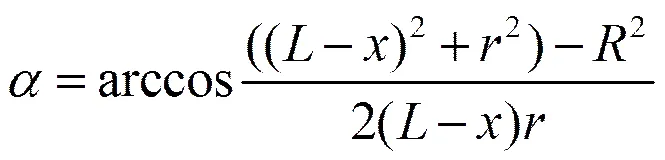
而弹翼的展开角度与拉力杆位移间的关系为：

将上述方程联立起来，组成内弹道方程组，按数学模型选好合适的算法，利用Matlab软件编写程序，完成整体仿真模型的建立。

3 数值模拟与试验分析

3.1 数值模拟计算结果

依据建立的数学模型为基础，采用Matlab编制了燃气作动筒弹翼展开过程的计算与分析软件，本实例是在产品尺寸确定的情况下，以装药药型和类型作为输入参数，气体压强、位移时间、旋转角度作为输出参数，获得变化曲线图，从而确定最合理的装药质量和药型，如图4所示。

3.2 试验结果

验证试验采用压力传感器分别测试燃气作动筒燃烧腔压力和工作腔压力。在活塞杆上方对应平行位置安装拉杆式位移传感器，测试活塞杆位移；在弹翼转轴中心位置安装角度传感器，测试弹翼转动角度。将上述信号转化为电信号，通过放大器将电信号放大并进行数据采集，将采集的数据通过示波器保存成——，——，——曲线和数据文本文档，如图5所示。将试验数据与仿真计算结果进行对比，见表1。

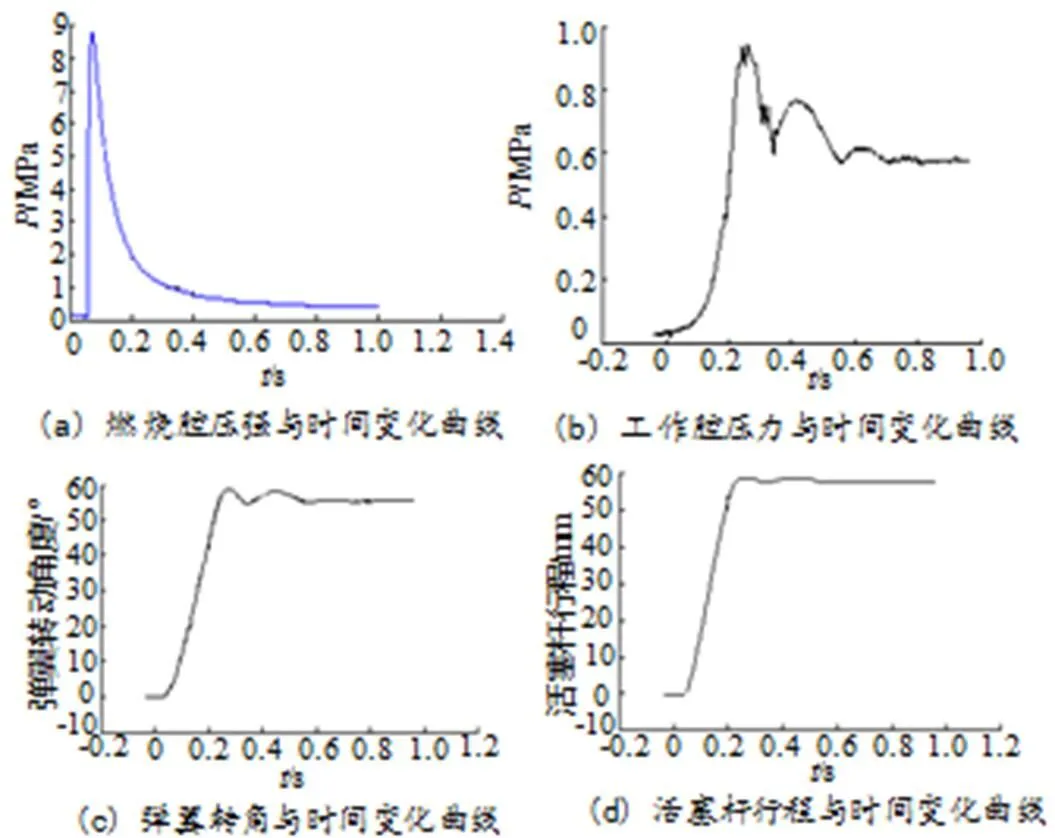
图5 弹翼展开燃气作动筒试验测试曲线图

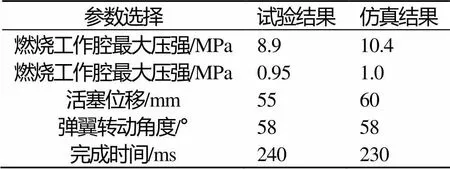
表1 试验值与仿真值的比较

试验数据与仿真数值对比可得：燃烧腔最大压强值相差1.5MPa，活塞位移相差5mm，转动角速度一致。计算过程和实测过程基本一致，可对燃气作动筒内弹道进行预估。

4 结论

本文为弹翼展开燃气作动筒结构设计和装药设计提供了理论研究的方法，并通过试验验证了所建模型的合理性。采用经典内弹道理论建模，运用MATLAB软件编制了内弹道仿真计算程序，从宏观上预测各物理量。鉴于该作动筒及弹翼展开机构复杂，在今后的研究中需进一步细化，采用多维两相流理论来建模，进一步研究作动筒复杂的内弹道过程及膛内燃气流动过程，为优化系统设计提供更详细有力的理论指导。

[1] 李莉,任茶仙,张铎.折叠翼机构展开动力学仿真及优化 [J].强度与环境,2007, 34 (1):17-21．

[2] 姚小宁,屠小昌,黄运銮,等. 弹翼展开机构中燃气作动筒的运动模型 [J]. 弹箭与制导学报, 2010, 32(5):48-50.

[3] 翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006.

[4] 金志明.枪炮内弹道学[M].北京:北京理工大学出版社, 2004.

[5] 张石玉,唐金兰,任华.燃气作动筒式折叠弹翼展开过程分析[J].固体火箭技术, 2010,33(5):481-485.

The Assessment Study of Combustion Gas Cylindric Actuator for Folded Wings

YANG Min-peng,YANG Shu-bin,TU Xiao-chang,LIANG Hong ,SHI Quan-li,CHEN Jing

(Shaanxi Applied Physics and Chemistry Research Institute,Xi'an,710061)

In order to effectively control the process of combustion gas actuating folded wings, the interior ballistic phenomenon and the process of the gas cylindric actuator was researched. Base on the classical interior ballistic theory, using matlab calculation program, the numerical simulation of combustion gas actuating folded wings was completed. Compared with the experimental results, the theoretical model was verified, which can provide theoretical basis for the structure design of the gas actuator.

Combustion gas cylindric actuator；Interior ballistic；State equation；Numerical simulation

1003-1480（2016）02-0029-04

TJ450.2

A

2015-11-04

杨敏鹏（1988-），男，在读硕士研究生，主要从事先进火工设计技术研究。