复习课有效渗透“开放与探究”试题的探究与思考

陈国星

开放探究型问题，可分为开放型问题和探究型问题两类.

开放型问题是相对于有明确条件和明确结论的封闭型问题而言的，它是条件或结论给定不完全、答案不唯一的一类问题.这类试题已成为近年中考的热点，重在考查同学们分析、探索能力，以及思维的发散性，但难度适中.

探究型问题是指命题中缺少一定的条件或无明确的结论，需要经过推断、补充并加以证明的一类问题.

一、解题策略

由于开放探究型试题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖，构思精巧，具有相当的深度和难度，所以要求同学们在复习时，首先对基础知识一定要全面复习，并力求扎实牢靠；其次要加强对解答这类试题的练习，注意各知识点之间的因果联系，选择合适的解题途径完成最后的解答.由于题型新颖、综合性强、结构独特等，此类问题的一般解题思路并无固定模式或套路，但是可以从以下几个角度考虑：

1.利用特殊值（特殊点、特殊数量、特殊线段、特殊位置等）进行归纳、概括，从特殊到一般，从而得出规律.

2.反演推理法（反证法），即假设结论成立，根据假设进行推理，看是推导出矛盾还是能与已知条件一致.

3.分类讨论法.当命题的题设和结论不唯一确定，难以统一解答时，则需要按可能出现的情况做到既不重复又不遗漏，分门别类加以讨论求解，将不同结论综合归纳得出正确结果.

4.类比猜想法，即由一个问题的结论或解决方法类比猜想出另一个类似问题的结论或解决方法，并加以严密论证.

以上所述并不能全面概括此类命题的解题策略，在具体操作时应更注重数学思想方法的综合运用.

二、考点精讲

（一）开放型问题

考点一：条件开放型

条件开放题是指结论给定，条件未知或不全，需探求与结论相对应的条件.解这种开放问题的一般思路是：由已知的结论反思题目应具备怎样的条件，即从题目的结论出发，逆向追索，逐步探求.

例1：请从以下三个等式中，选出一个等式填在横线上，并加以证明.

等式：AB=CD，∠A=∠C，∠AEB=∠CFD

已知：AB∥CD，BE=DF，？摇？摇 ？摇？摇.

求证：△ABE≌△CDF.

证明：

评注：解决此类问题的一般方法是：由已知的结论反思题目应具备怎样的条件，即从题目的结论出发，结合图形挖掘条件，逆向追索，逐步探寻，是一种分析型思维方式.它要求解题者善于从问题的结论出发，逆向追索，多途寻因；当然也要注意已有的条件及由已有的条件推导出的条件，不可重复条件，也不能遗漏条件.

考点二：结论开放型

给出问题的条件，让解题者根据条件探索相应的结论并且符合条件的结论往往呈现多样性，这些问题都是结论开放问题.这类问题的解题思路是：充分利用已知条件或图形特征，进行猜想、类比、联想、归纳，透彻分析出给定条件下可能存在的结论，然后经过论证作出取舍.

例2：现有四条钢线，长度分别为（单位：）7、6、3、2，从中取出三根连成一个三角形，这三根的长度可以为？摇？摇 ？摇？摇.（写出一种即可）

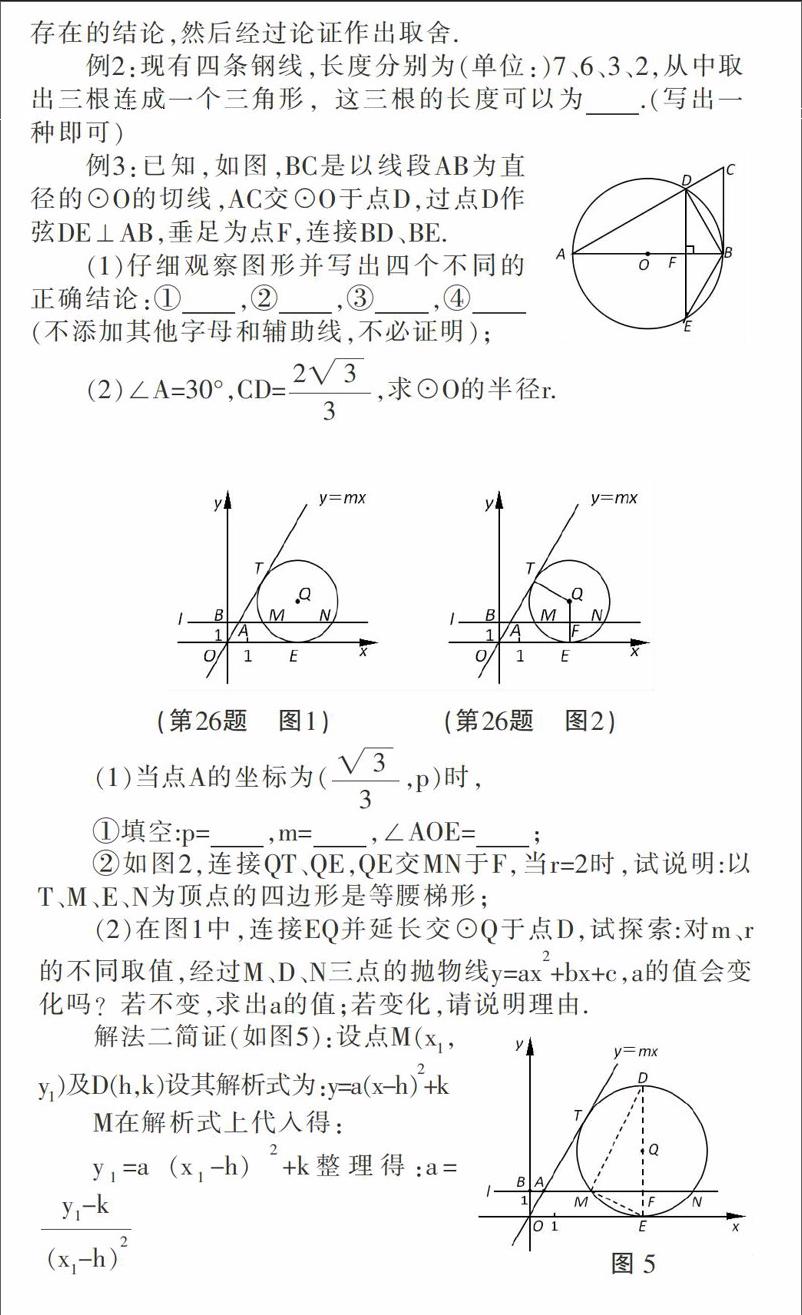
例3：已知，如图，BC是以线段AB为直径的⊙O的切线，AC交⊙O于点D，过点D作弦DE⊥AB，垂足为点F，连接BD、BE.

（1）仔细观察图形并写出四个不同的正确结论：①？摇？摇 ？摇？摇，②？摇 ？摇？摇？摇，③？摇？摇 ？摇？摇，④？摇？摇 ？摇？摇（不添加其他字母和辅助线，不必证明）；

（2）∠A=30°，CD=，求⊙O的半径r.

评注：此类问题可以充分考查学生知识的掌握水平，并对问题作更深入的探究.在平常的教学过程中，应该提倡此类题目，让学生充分挖掘题目中所能得到的更多结论.解结论开放型问题时要充分利用已知条件或图形特征，进行猜想、归纳、类比，透彻分析出给定条件下可能存在的结论现象，然后经过论证作出取舍，这是一种归纳类比型思维.它要求解题者充分利用条件进行大胆而合理的猜想，发现规律，得出结论，这类题主要考查解题者的发散性思维能力和知识应用能力.

考点三：策略开放型

一般指解题方法不唯一或解题途径不明确的问题，这类问题要求解题者善于标新立异，优化解题方案和过程.在复习中既要重视基础知识的复习，又要加强变式训练和数学思想方法的研究，切实提高分析问题、解决问题的能力.

例4：如图1，在第一象限内，直线y=mx与过点B（0，1）且平行于x轴的直线l相交于点A，半径为r的⊙Q与直线y=mx，x轴分别相切于点T、E，且与直线l分别交于不同的M、N两点.

评注：在第（2）的解决过程中，多达十几种解法，至少有这三种大的思考方向，一是：平移不变的性质，把抛物线平移到合适的位置，从而有效减少参数，使问题得到有效解决；二是：利用抛物线的几何性质，从而简化问题；三是：利用同一条线段的两种不同表示方法列等式进行求解.在平常的教学中，应该多注重题目的一题多解及多题归一的教学.此类问题的一般解法：通常需要模仿、类比、试验、创新和综合运用所学知识，建立合理的数学模型，从而使问题得以解决.策略开放型问题的解题方法一般不唯一或解题路径不明确，要求解题者不墨守成规，敢于创新，积极发散思维，优化解题方案和过程.

考点四：编制开放型

此类问题是指条件、结论、解题方法都不全或未知，仅提供一种问题情境，需要我们补充条件，设计结论，寻求解法的一类题，常令学生一时不知所措.

例5：某校九年级两个班各为玉树地震灾区捐款1800元.已知2班比1班人均捐款多4元，2班的人数比1班的人数少10%.请你根据上述信息，就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题，并写出解题过程.

评注：对于此类编制开放型问题，是一类新型的开放型问题，它要求学生的思维较发散，写出符合题意的正确答案即可，难度要求不大，但学生容易犯想当然的错误，叙述不够准确，如单位的问题、符合实际等要求，在解题中应该注意防范.

（二）探究型问题

考点五：条件探究型

此类问题结论明确，而需探究发现使结论成立的条件的题目.

（1）求h的值；

（2）通过操作、观察，算出△POQ面积的最小值（不必说理）；

（3）过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中，四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指出四边形的形状.

评注：此类型的问题其本质与条件探索型相差不大，只是需要多一步作猜想.

考点七：存在探究型

此类问题在一定的条件下，需探究发现某种数学关系是否存在的题目.

例8：我们容易发现：反比例函数的图像是一个中心对称图形.你可以利用这一结论解决问题.

如图，在同一直角坐标系中，正比例函数的图像可以看做是：将轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数y=图像分别交于第一、三象限的点B、D，已知点A（-m，0）、C（m，0）.

（1）直接判断并填写：不论α取何值，四边形ABCD的形状一定是？摇？摇 ？摇？摇；

（2）①当点B为（p，1）时，四边形ABCD是矩形，试求p、α、和m有值；

②观察猜想：对①中的m值，能使四边形ABCD为矩形的点B共有几个？（不必说理）

（3）试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由.

评注：存在性探究的题型的固定的几种类型，如：相似、等腰、直角、四边形、面积相等问题，比较容易训练成模型，因此在近几年的全国范围内的考查中，此类问题正在进一步弱化.解答此类问题的一般思路是：先假设存在，然后由此出发，结合已知条件进行计算推理论证，导出某个结果.若该结果合理，则说明假设成立，由此得出问题的答案；如果该结果不合理，则说明假设不成立，所探索的条件或结论不存在.