翼型参数对旋翼悬停气动噪声特性影响
刘大伟,黄 俊,王 英,姬金祖
(北京航空航天大学 航空科学与工程学院,北京 100191)
翼型参数对旋翼悬停气动噪声特性影响
刘大伟,黄俊,王英,姬金祖
(北京航空航天大学 航空科学与工程学院,北京 100191)
基于运动嵌套网格的欧拉方程建立了旋翼流场的数值模拟方法。以旋翼气动性能仿真结果作为输入,应用FARASSATE1A公式发展了适用于旋翼气动噪声的计算程序。通过与C-T旋翼的实验数据对比,验证了方法的有效性。在此基础上,通过改变旋翼桨叶翼型的厚度、弯度以及最大弯度位置研究了翼型参数对旋翼悬停气动噪声特性的影响。研究结果表明,翼型厚度是决定旋翼厚度噪声的关键因素,旋翼载荷噪声决定于旋翼桨叶表面压力分布。旋翼厚度噪声主要受翼型厚度变化影响,旋翼载荷噪声则主要受翼型最大弯度和最大弯度位置的影响。翼型参数变化不会明显改变旋翼气动噪声的方向特性。
翼型参数;旋翼流场;旋翼气动;旋翼噪声;方向特性
直升机的噪声是限制现代直升机广泛应用的主要原因之一[1-3],直升机降噪设计引起了越来越多的直升机厂商的重视。旋翼气动噪声是直升机最主要噪声源,具有传播距离远、空气中衰减速度慢的特点,是直升机降噪设计的主要研究目标。
旋翼噪声控制分为主动降噪和被动降噪两种方式。主动降噪主要包括高阶谐波控制、单独桨叶控制、桨叶后缘控制以及桨尖喷气方法等[4-8]。由于控制技术复杂且实现成本高昂,目前以上几种主动降噪方法都无法实际应用到直升机旋翼系统设计中。被动式降噪方法主要是通过改变桨叶的形状或者气动布局来降低直升机的噪声辐射,从而降低军用直升机的声学可探测性以及改善民用直升机的舒适性。研究认为,目前被动式降噪方法是最为可行和易于实现的直升机降噪设计方法,国内外学者已经开展了许多关于直升机被动降噪的研究[8-15],尤其是优化桨叶形状降低旋翼噪声。宋文萍和王立群等通过改变旋翼桨尖厚度,削尖度以及后掠等变化研究了旋翼桨尖形状对气动噪声的定量影响[13-14]。而关于旋翼桨叶翼型参数对气动噪声的影响则相对很少。本文保持桨叶形状参数不变,采用NACA四位翼型,通过单独改变翼型最大厚度、最大弯度以及最大弯度位置来研究桨叶翼型参数对旋翼气动噪声的影响。
本文应用旋翼CFD方法[16-18]与基于FW-H方程[19-20]的FARASSATE1A公式[21-26]相结合的方法,建立了旋翼气动噪声数值模拟方法。通过与相关参考文献中的实验数据和仿真结果[27-28]对比,验证了本文数值模拟方法的有效性。在此基础上,通过改变旋翼桨叶翼型的厚度、弯度以及最大弯度位置研究了翼型参数对旋翼悬停气动噪声特性的影响,进而为直升机旋翼设计提供依据。
1 计算模型
本文中基准旋翼选用美国NASA的Caradonna-Tung(C-T)试验旋翼[27],该旋翼由平面形状为矩型的两片无扭转矩形桨叶组成。桨叶半径R=1.143 m,桨叶弦长C=0.190 5 m。旋翼旋转速度设置为Ω=1 250 RPM,即对应的桨尖马赫数为0.439,旋翼处于亚音速悬停状态。旋翼桨距设置为8°,旋翼轴倾角设置为0°。图1为旋翼旋转方向及噪声观察点位置示意图。旋翼噪声观察点位于旋翼旋转平面下15°方位角方向,观察点距离旋翼桨榖的水平距离为2R。
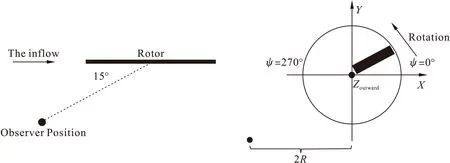
图1 旋翼旋转方向和观察点位置示意图
2 计算方法及验证
2.1旋翼流场计算方法及结果验证
直升机旋翼工作时,在周期性旋转的同时,还要进行挥舞、摆振和变距运动。旋翼流场存在着复杂的气动现象,因此旋翼流场的准确数值模拟一直是旋翼空气动力学研究的难点和热点。本文应用基于运动嵌套网格方法的非定常欧拉方程进行旋翼流场的计算求解,控制方程为
其中,Q为守恒变量,F为通量矢量,Λ表示源项。V和S分别表示控制体积和控制体表面积。计算过程中,每一时间步旋翼旋转0.075°,整个旋翼旋转周期划分为4 800步。旋翼旋转5圈后,数值模拟结果收敛。背景网格和桨叶网格划分如图2所示。
为了验证旋翼流场数值模拟方法的有效性,将数值模拟得到的桨叶表面压力分布与广泛应用于旋翼流场模拟验证的Caradonna-Tung 旋翼实验数据[27]进行对比,结果如图3所示。
由图3可见,本文中旋翼流场的数值模拟结果与实验数据吻合很好。这说明本文建立的旋翼流场计算方法能够准确模拟旋翼流场,进而为旋翼气动噪声计算提供准确载荷输入。
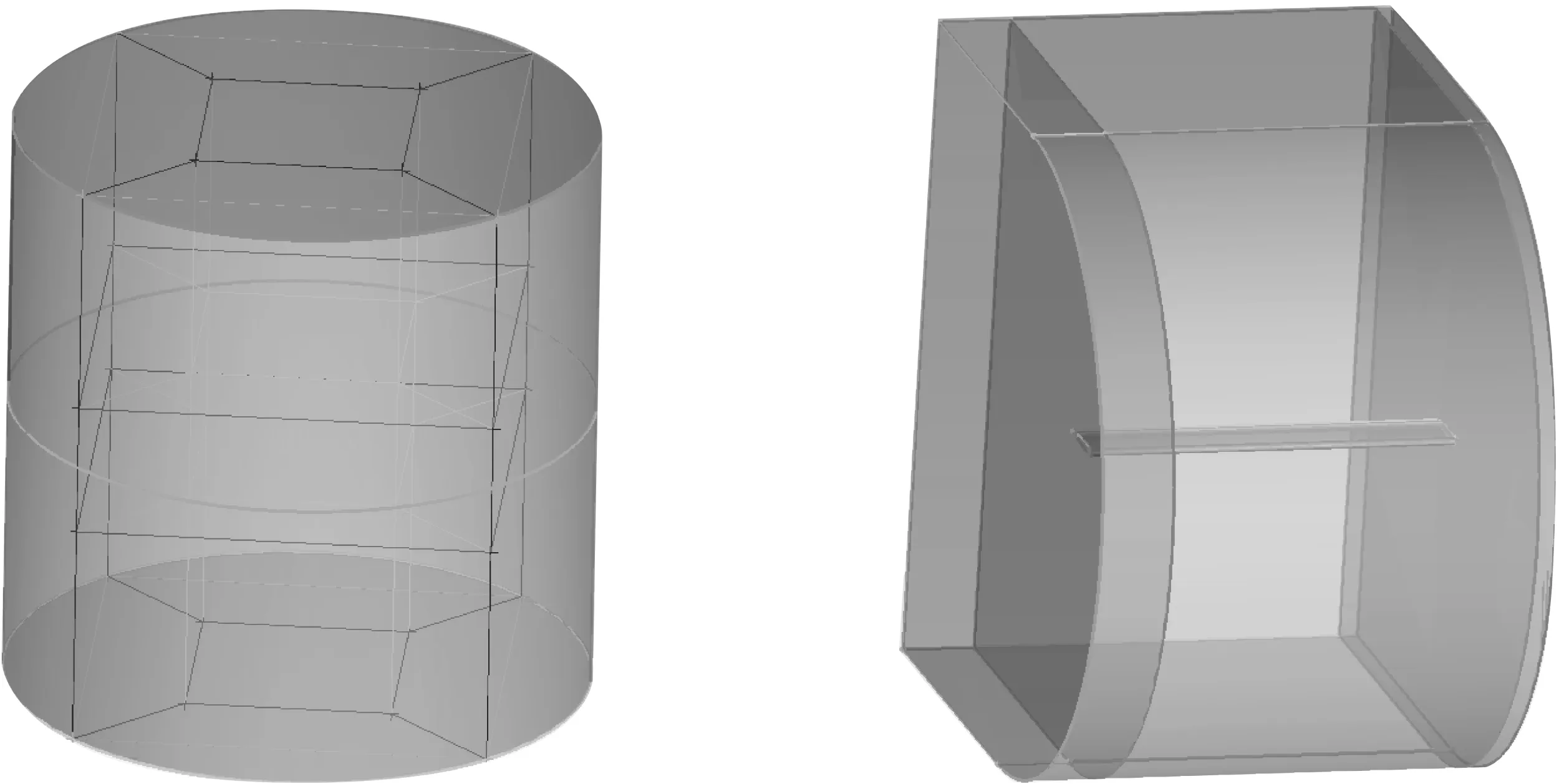
图2 旋翼背景网格区域和单块桨叶网格划分区域
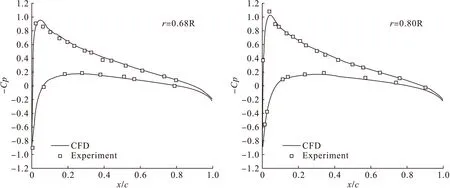
图3 桨叶弦向截面压力分布CFD与实验数据的对比
2.2旋翼气动噪声计算方法结果验证
基于莱特希尔的声学类比理论的FW-H方程是目前旋翼气动噪声预测的最重要方法。FW-H方程表达式如下式所示
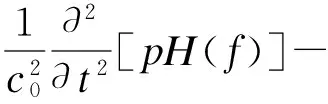
其中,p代表声压,ρ0和c0分别表示未扰动的空气密度和声速,Tij为莱特希尔应力张量,H为海维赛德(Heaviside)广义函数。公式右端3项分别表示单级子、偶极子及四极子噪声,即对应旋翼的厚度噪声、载荷噪声及四极子噪声。
20世纪80年代,Farassat在FW-H方程基础上,应用广义函数理论推导出了更适合计算机编程数值模拟计算的Fassate1A公式。公式如下所示
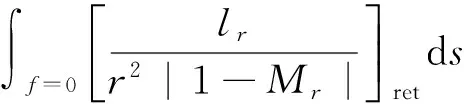
为证明旋翼气动噪声计算结果的可信性,将本文仿真计算结果与相关参考文献旋翼气动噪声实验结果对比[28]。计算状态为叶尖马赫数Mtip=0.88,观察位置坐标为(5.65,0,0)m,旋翼轴倾角为0°。由图4可见,本文计算得到的旋翼气动噪声时间变化历程与实验数据吻合很好,能够准确有效地预测直升机旋翼旋转噪声。
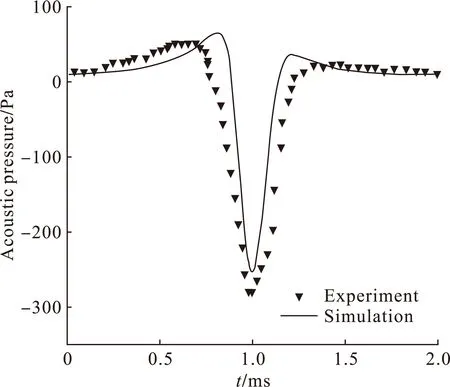
图4 直升机旋翼气动噪声声压变化历程与试验结果对比
3 结果分析
旋翼桨叶翼型参数主要包括翼型最大厚度、翼型最大弯度以及最大弯度位置。翼型参数对翼型的空气动力学特性有着重要影响,进而影响旋翼流场及气动声学特性。为了便于分析比较不同翼型参数对旋翼气动声学特性的影响,本文选用具有解析表达式的NACA四位翼型作为研究对象,通过改变旋翼桨叶翼型参数,分析翼型参数对旋翼气动声学特性的影响。
3.1翼型厚度对旋翼气动噪声特性影响
为研究翼型最大厚度对旋翼气动声学特性的影响,选用NACA0008、NACA0010以及NACA0012三种厚度依次递增的翼型作为基准旋翼桨叶翼型。图5为不同翼型厚度变化时一个旋翼旋转周期内旋翼厚度噪声和载荷噪声的时域声压曲线。由图可见,随着翼型厚度的逐渐增大,厚度噪声尖锐负峰值有着明显的提升。厚度噪声是由桨叶厚度使周围的空气发生位移而产生的,旋转运动的桨叶使得位于桨盘平面上的流体不断被具有厚度的旋转桨叶所占据,从而使得当地流体发生周期性的体积压缩而导致密度增大。所以翼型厚度为气动厚度噪声最关键因素,随着翼型厚度的增大,旋翼厚度噪声有着明显增大。相比于厚度噪声,当翼型厚度逐渐增大时旋翼载荷噪声基本不变,这是由于载荷噪声是由桨叶上产生的力对周围流体作用而产生的。旋转的桨叶使得位于桨盘平面附近的流体不断受到旋转桨叶叶片各叶素上力的作用,根据牛顿第二定律,在当地叶素力作用下,流体就会产生指点速度的周期性变化,而质点速度的变化也将导致当地流体压力的变化从而产生声压。当翼型厚度增大时,如图6所示桨叶表面压力分布基本不变,即旋翼气动载荷没有明显变化,进而旋翼载荷噪声基本不会发生改变。
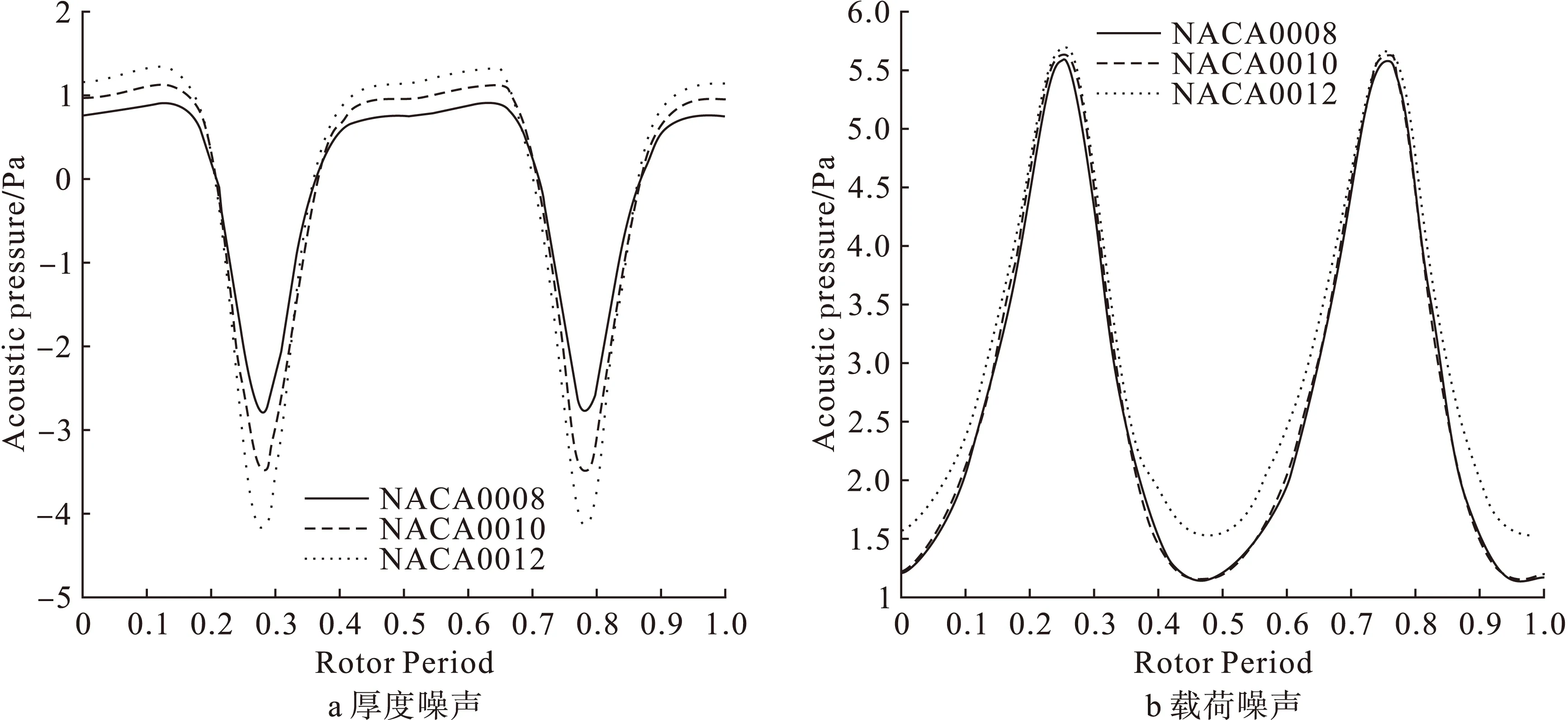
图5 不同翼型厚度旋翼气动噪声
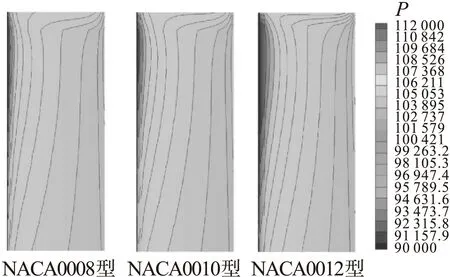
图6 不同翼型厚度桨叶上表面压力分布(压力单位:Pa)
由于厚度噪声和载荷噪声分别是由于具有厚度的桨叶运动和桨叶表面的气动载荷与当地气体作用的结果,所以厚度和载荷噪声在空间各方位的噪声大小与桨叶运动和载荷在各方向上分布相关,因而在整个噪声辐射空间,直升机旋翼的噪声辐射具有明显的方向特性。为分析翼型厚度对旋翼气动噪声的方向特性的影响,图7给出了改变翼型厚度时,垂直于旋翼旋转平面上(YZ面)旋翼厚度噪声和载荷噪声周向分布。由图可见,直升机的厚度噪声最大幅值主要分布在旋翼的旋转平面上下,而在垂直于旋翼旋转平面方向几乎为0。旋翼载荷噪声最大幅值则分布在垂直于旋翼旋转平面方位,而最小值在旋翼旋转平面方向。
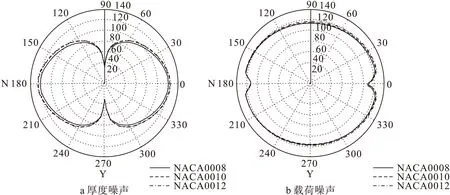
图7 不同翼型厚度旋翼气动噪声方向特性(声压级单位:dB)
当翼型厚度增大时,垂直于桨叶旋转平面的YZ平面上沿周向各点噪声幅值变化与观察点噪声变化趋势相同,厚度噪声幅值随着翼型厚度的增大而增大,而载荷噪声幅值基本不受翼型厚度变化的影响。
3.2翼型弯度对旋翼气动噪声特性影响
为研究翼型最大弯度对旋翼气动声学特性的影响,选用NACA2212、NACA4412以及NACA6412三种最大弯度依次递增的翼型作为基准旋翼桨叶翼型来分析最大翼型弯度的影响。
图8为不同翼型厚度变化时一个旋翼旋转周期内旋翼厚度噪声和载荷噪声的时域声压曲线。由图可见,随着翼型弯度的逐渐增大,旋翼厚度噪声基本不发生变化,这是由于旋翼厚度噪声主要受翼型厚度影响,单独改变翼型的弯度不会引起旋翼厚度噪声的变化。图 9 为翼型最大弯度变化时,桨叶上表面压力分布,随着翼型最大弯度的增大,桨叶表面低压区域沿弦向后移,且负压区面积增大。桨叶载荷分布更加不均,从而引起载荷噪声随翼型最大弯度增大而变大。

图8 不同翼型最大弯度对旋翼气动噪声影响
图10给出了改变翼型最大弯度时,垂直于旋翼旋转平面上(YZ面)旋翼厚度噪声和载荷噪声周向分布。由图可见当翼型最大弯度变化时,YZ平面上沿周向各点噪声幅值变化与观察点噪声变化趋势相同,厚度噪声幅值基本没有明显变化,而载荷噪声幅值随着翼型最大弯度增大而显著增加。翼型最大弯度不会明显改变旋翼气动噪声方向特性。
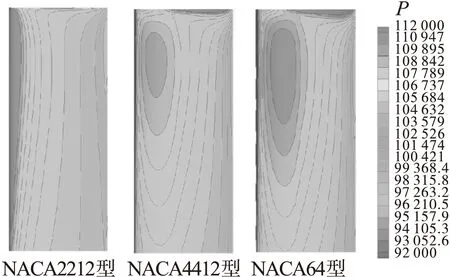
图9 不同翼型最大弯度桨叶上表面压力分布(压力单位:Pa)
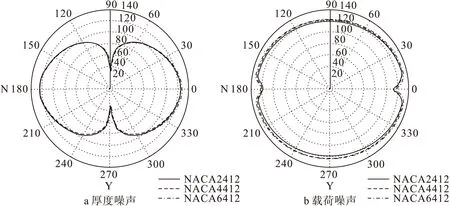
图10 不同翼型最大弯度对旋翼噪声方向特性影响(声压级单位:dB)
3.3翼型最大弯度位置对旋翼气动噪声特性影响
为研究翼型最大弯度位置对旋翼气动声学特性的影响,选用NACA2212、NACA2412 以及NACA2612三种最大弯度位置依次沿弦向后移的翼型作为基准旋翼桨叶翼型来分析最大翼型弯度位置的影响。
图11为翼型最大弯度位置变化时一个旋翼旋转周期内旋翼厚度噪声和载荷噪声的时域声压曲线。由图可见,随着翼型最大弯度位置沿弦向后移,旋翼厚度噪声基本不发生变化,这是由于旋翼厚度噪声主要受翼型厚度影响,单独改变翼型的弯度分布不会引起旋翼厚度噪声的变化。图 9 为翼型最大弯度位置变化时,桨叶上表面压力分布。如图12所示,随着翼型最大弯度位置沿弦向后移,桨叶表面等压线分布密度增大,桨叶载荷分布更加不均,从而引起载荷噪声随翼型最大弯度位置后移而变大。
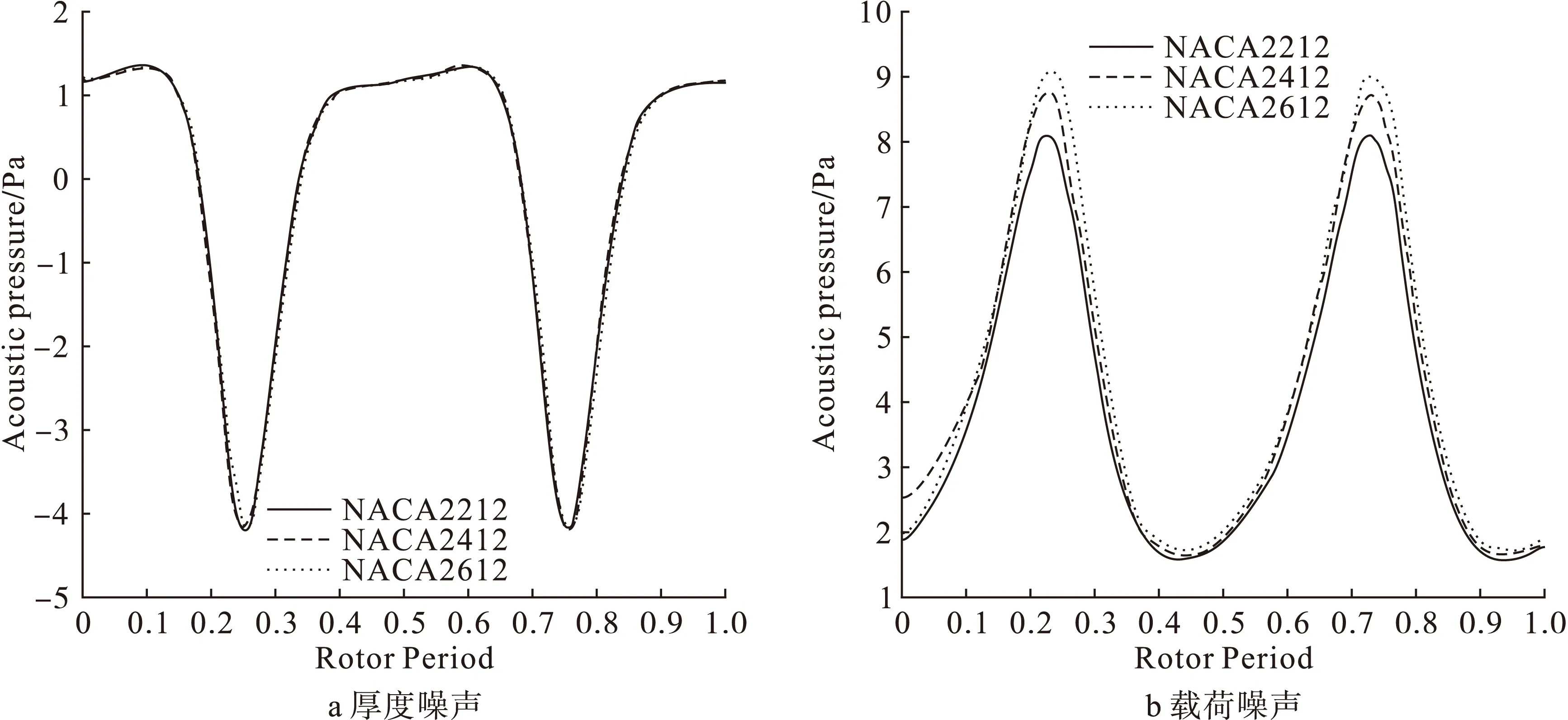
图11 不同翼型最大弯度位置对旋翼气动噪声影响
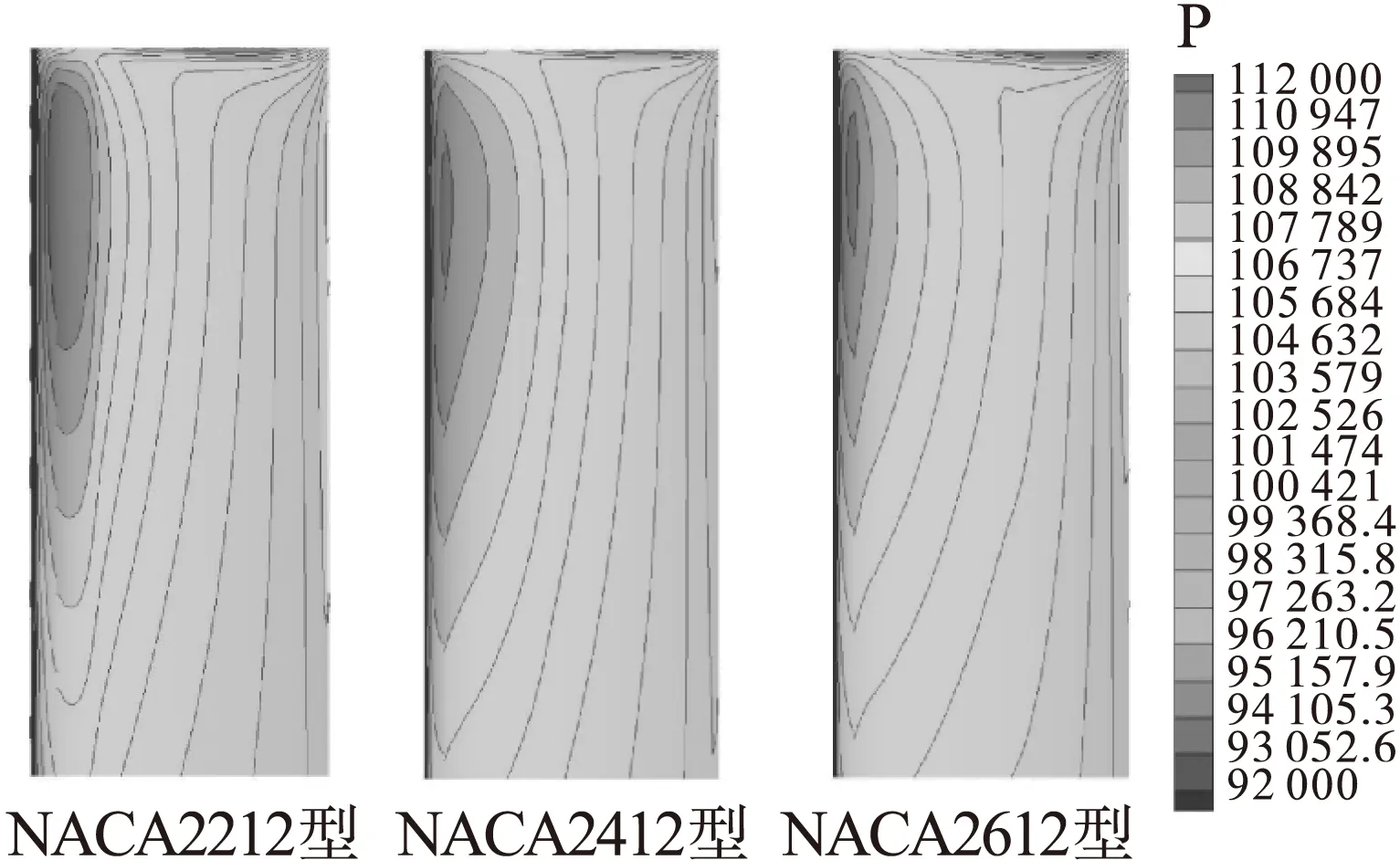
图12 不同翼型最大弯度桨叶上表面压力分布(压力单位:Pa)
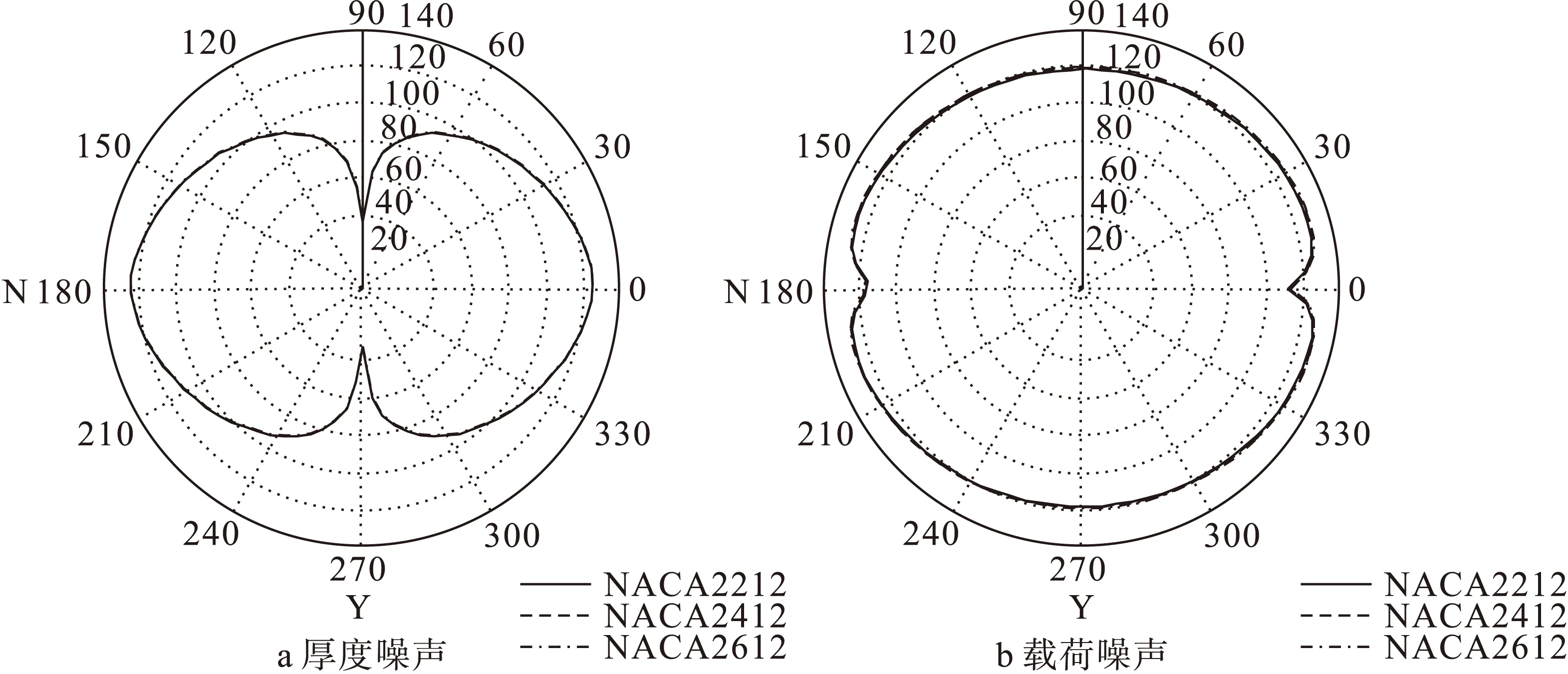
图13 不同翼型最大弯度位置对旋翼噪声方向特性影响(声压级单位:dB)
图13给出了改变翼型最大弯度位置时,垂直于旋翼旋转平面上(YZ面)旋翼厚度噪声和载荷噪声周向分布。由图可见当翼型最大弯度位置发生变化时,YZ平面上沿周向各点噪声幅值变化与观察点噪声变化趋势相同,厚度噪声幅值基本没有明显变化,而载荷噪声幅值随着翼型最大弯度沿弦向位置后移而显著增加,翼型最大弯度不会明显改变旋翼气动噪声方向特性。
4 结论
本文应用旋翼CFD方法与基于FW-H方程的FARASSATE1A公式相结合的方法,建立了旋翼气动噪声的数值模拟方法。在此基础上,通过改变旋翼桨叶翼型的厚度、弯度以及最大弯度位置研究了翼型参数对旋翼悬停气动噪声特性的影响,得到如下结论:
(1)翼型厚度是决定旋翼厚度噪声的关键因素,厚度噪声负峰值随着翼型厚度增加而增大,翼型最大弯度及最大弯度位置变化不会引起旋翼厚度噪声的明显变化。
(2)旋翼载荷噪声主要决定于旋翼桨叶表面压力分布。翼型厚度变化基本不会引起旋翼载荷噪声的显著变化,当翼型最大弯度增大或最大弯度位置沿弦向后移,旋翼载荷噪声增大。
(3)翼型参数变化时,沿垂直于旋翼旋转平面周向各点厚度噪声及载荷噪声同观察点位置噪声值变化趋势相同,说明翼型参数变化不会明显改变旋翼气动噪声的方向特性。
[1]BRENTNER K S.Prediction of helicopter rotor discrete frequency noise-a computer program incorporating realistic motions and advanced acoustic formulation[C].NASA-TM-87721,1986.
[2]RICHARD SICKENBERGER.Modeling helicopter near-horizon harmonic noise due to transient maneuvers[D].Maryland:University of Maryland College Park,2012.
[3]ALLEN C B.An unsteady multiblock multigrid scheme for lifting forward flight rotor simulation[J]International Journal for Numerical Methods in Fluids,2004,45(9):973-984.
[4]YU Y H,TUNG C,van der Wall B,et al.The HART-II test:Rotor Wakes and Aeroacoustics with Higher-Harmonic Pitch Control (HHC) Inputs[C].Proceedings of the AHS 58th Annual Forum,2002.
[5]JACKLIN S A,BLAAS A,TEVES D,et al.Reduction of helicopter bvi noise,vibration,and power consumption through individual blade control[C].Proceedings of the AHS 51st AnnualForum,1995.
[6]SIM B.WC.Suppressing in-plane,low-frequency helicopter harmonic noise with active controls[C].American Helicopter Society Technical Specialists′ Conference,San Francisco:CA,2008.
[7]SARGENT D C.Active jet acoustic control of low frequency in-plane helicopter harmonic noise[D].Maryland:University of Maryland College Park,2012.
[8]DESOPPER A,LAFON P,PHILIPPE J J,et al.Effect of an anhedral sweptback tip on the performance of a helicopter rotor[J].Vertica,1988,12(4):345-355.
[9]尹建平.直升机噪声及其控制技术的研究[D].南京:南京航空航天大学,1996.
[10]蔡伟,王阳,徐国华.应用非均布桨叶设计设计方法的旋翼降噪技术研究[J].直升机技术,2008,155(3):86-91.
[11]王阳,宋辰瑶,徐国华.直升机飞行参数对起降过程中旋翼桨涡干扰噪声影响的分析[J].空气动力学报,2010,28(3):322-325.
[12]王阳.直升机旋翼气动噪声的计算机降噪方法研究[D].南京:南京航空航天大学,2011.
[13]王立群,宋文萍.旋翼桨尖形状对噪声影响量级的研究[J].航空学报,2000,21(1):48-51.
[14]宋文萍,韩忠华,王立群,等.旋翼桨尖几何形状对旋翼气动噪声影响的定量计算分析[J].计算物理,2001,18(6):569-572.
[15]郭旺柳,宋文萍,许建华,等.旋翼桨尖气动/降噪综合优化设计研究[J].西北工业大学学报,2012,30(1):73-79.
[16]ZHAO Q J,XU G H,ZHAO J G.Numerical simulations of the unsteady flowfield of helicopter rotors on moving embedded grids[J].Aerospace science and technology,2005,9(2):117-124.
[17]MAMOUS M,KHALID M.Time-accurate flow simulations past helicopter rotors in hover and forward flight conditions using chimera grid technique[J].Canadian Aeronautics and Space Journal,2006,52(4):135-148.
[18]LEISHMAN J G.Principles of helicopter aerodynamics with cd extra[M].Cambridge:Cambridge University Press,2006.
[19]WILLIAMS J E F,HAWKINGS D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1969,264(1151):321-342.
[20]LIGHTHILL M J.On sound generated aerodynamically.I.General theory[J]Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.The Royal Society,1952,211(1107):564-587.
[21]FARASSAT F.Theory of noise generation from moving bodies with an application to helicopter rotors[M].National Aeronautics and Space Administration,1975.
[22]FARASSAT F,KENNETH S.BRENTNER.The uses and abuses of the acoustic analogy in helicopter rotor noise prediction[J].Journal of the American Helicopter Society,1988,33(1):29-36.
[23]FARASSAT F.Derivation of formulations 1 and 1a of farassat[R].NASA TM 214853,2007.
[24]FARASSAT F,MYERS M K.Extension of kirchhoff's formula to radiation from moving surfaces[J].Journal of Sound and Vibration,1988,123(3):451-460.
[25]FARASSAT F,GEORGE P SUCCI.The prediction of helicopter rotor discrete frequency noise[J].American Helicopter Society,1982(1):497-507.
[26]F FARASSAT,G P SUCCI.The prediction of helicopter rotor discrete frequency noise[J]Vertica,1983(7):309-320.
[27]F X CARADONNA,C TUNG.Experimental and Analytical Studies of a Model Helicopter Rotor in Hover[J].Vertica,1980,5(2):149-161.
[28]BRENTNER K S,FARASSAT F.Modeling aerodynamically generated sound of helicopter rotors[J].Progress in Aerospace Sciences,2003,39(2):83-120.
(责任编辑:宋丽萍英文审校:赵欢)
Effects of airfoil parameters on hover rotor aerodynamic acoustic performance
LIU Da-wei,HUANG Jun,WANG Ying,JI Jin-zu
(School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China)
A numerical simulation of rotor flow-field was proposed based on the unsteady Euler equations with moving chimera grid.Calculation procedure predicting helicopter rotor aerodynamic and noise was developed using the formula of FARASSATE1A and making simulation results of rotor aerodynamic performance as an input.A comparison against the experimental data of C-T rotor verified the availability of the simulation.The effects of airfoil parameters on rotor acoustics were analyzed by changing airfoil thickness,camber,and max camber position.The results show that airfoil thickness is a crucial influence factor for rotor thickness noise.The loading noise highly depends on the pressure distribution of blade surface,associated with biggest bending of airfoil and its position.The airfoil parameters of rotor blade do not remarkably change the directivity of thickness and loading noise.
airfoil parameter;rotor flow-field;rotor aerodynamic;rotor acoustic;directivity
2016-03-22
国家自然科学基金(项目编号:51307004)
刘大伟(1985-),男,河北唐山人,博士研究生,主要研究方向:直升机空气动力学,E-mail:buaapebble@sina.com。
航空宇航工程
2095-1248(2016)04-0001-08
V275.1
A
10.3969/j.issn.2095-1248.2016.04.001

