L-octo-algebras

An Hui-hui and Wang Zhi-chun

(School of Mathematics,Liaoning Normal University,Dalian,Liaoning,116029)

Communicated by Du Xian-kun

L-octo-algebras

An Hui-hui and Wang Zhi-chun

(School of Mathematics,Liaoning Normal University,Dalian,Liaoning,116029)

Communicated by Du Xian-kun

L-octo-algebra with 8 operations as the Lie algebraic analogue of octoalgebra such that the sum of 8 operations is a Lie algebra is discussed.Any octoalgebra is an L-octo-algebra.The relationships among L-octo-algebras,L-quadrialgebras,L-dendriform algebras,pre-Lie algebras and Lie algebras are given.The close relationships between L-octo-algebras and some interesting structures like Rota-Baxter operators,classical Yang-Baxter equations and some bilinear forms satisfying certain conditions are given also.

L-octo-algebra,L-quadri-algebra,bimodule

2010 MR subject classification:17A30,17B60

Document code:A

Article ID:1674-5647(2016)01-0057-13

10.13447/j.1674-5647.2016.01.04

1　Introduction

Octo-algebras are a remarkable class of Loday algebras(see[1]).Loday algebras which include dendriform trialgebras(see[2]–[3]),NS-algebras(see[4]),octo-algebras(see[5]), ennea-algebras(see[6])and dendriform-Nijenhuis algebras(see[4])were first introduced by Loday[7]in 1995 with motivation from algebraic K-theory.At first,they introduced due to their own interesting motivations,then they developed as independent algebraic systems. Loday algebras are closely related to the study of CYBE,O-operator,operads and so on (see[8]–[10]).

In this paper,we introduce the notion of L-octo-algebra and discuss the relationships among Lie algebra,L-dendriform algebra,L-quadri-algebras and L-octo-algebras.This paper is organized as follows:In Section 2,we recall some basic facts on pre-Lie algebras, L-dendriform algebras and L-quadri-algebras;The definition of L-octo-algebras and the associated L-quadri-algebras,L-dendriform algebras and pre-Lie algebras on L-octo-algebras are given in Section 3;We give the bimodules on L-quadri-algebras and the bimodule of theassociated L-quadri-algebras,L-dendriform algebras,pre-Lie algebras on L-octo-algebras and the construction of L-octo-algebras on L-quadri-algebras by O-operators on L-quadrialgebras,2-cocycle on L-quadri-algebra in Sections 4 and 5,respectively;Finally,we give the bilinear forms on L-octo-algebras and the LO-equation on L-octo-algebras in Section 6. Throughout this paper,all algebras are finite dimensional and over a field F of characteristic zero.

2　Pre-Lie Algebras,L-dendriform Algebras and L-quadri-algebras

Proposition 2.1[11]–[12]Let(A,◦)be a pre-Lie algebra.Then the commutator

[x,y]=x◦y−y◦x,x,y∈A(2.1)

defines a Lie algebra g(A),which is called the sub-adjacent Lie algebra of A.

Proposition 2.2[11]Let(A,◃,▹)be an L-dendriform algebra.If we define

x•y=x◃y+x▹y,x,y∈A,(2.2)

x◦y=x◃y−y▹x,x,y∈A,(2.3)

then(A,•)and(A,◦)are pre-Lie algebras,which are called the associated horizontal and vertical pre-Lie algebras.

Proposition 2.3[12]Let(A,↘,↗,↖,↙)be an L-quadri-algebra.

(1)(A,≻,≺)and(A,∨,∧)are dendriform algebras.They are called the associated vertical and depth L-dendriform algebra of(A,↘,↗,↖,↙);

(2)If we define

x◃y=x↘y−y↖x,x▹y=x↗y−y↙x,x,y∈A,(2.4)

then(A,◃,▹)is a dendriform algebra,which is called the associated horizontal L-dendriform algebra of(A,↘,↗,↖,↙).

3　L-octo-algebras

Definition 3.1[12]Let A be a vector space with eight bilinear products denoted by↘1,↘2,↗1,↗2,↖1,↖2,↙1↙2:A⊗A→A.(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)is called an L-octo-algebra if for any x,y,z∈A,

x↘2(y↘2z)−(x∗12y)↘2z=y↘2(x↘2z)−(y∗12x)↘2z,

x↘2(y↗2z)−(x∨12y)↗2z=y↗2(x≻2z)−(y∧12x)↗2z,

x↘2(y↗1z)−(x∨2y)↗1z=y↗1(x≻12z)−(y∧1x)↗1z,

x↗2(y≻1z)−(x∧2y)↗1z=y↘1(x↗12z)−(y∨1x)↗1z,

x↘2(y↘1z)−(x∗2y)↘1z=y↘1(x↘12z)−(y∗1x)↘1z,

x↘2(y↖1z)−(x↘2y)↖1z=y↖1(x∗12z)−(y↖1x)↖1z,

x↗2(y≺1z)−(x↗2y)↖1z=y↙1(x∧12z)−(y↙1x)↖1z,

x↗1(y≺12z)−(x↗1y)↖1z=y↙2(x∧1z)−(y↙2x)↖1z,

x↘1(y↙12z)−(x≻1y)↙1z=y↙2(x∨1z)−(y≺2x)↙1z,

x↘1(y↖12z)−(x↘1y)↖1z=y↖2(x∗1z)−(y↖2x)↖1z,

x↘2(y↙1z)−(x≻2y)↙1z=y↙1(x∨12z)−(y≺1x)↙1z,

x↘2(y↙2z)−(x≻12y)↙2z=y↙2(x∨2z)−(y≺12x)↙2z,

x↗2(y≺2z)−(x↗12y)↖2z=y↙2(x∧2z)−(y↙12x)↖2z,

x↘2(y↖2z)−(x↘12y)↖2z=y↖2(x∗2z)−(y↖12x)↖2z,

where

x∨iy=x↘iy+x↙iy,x∧iy=x↗iy+x↖iy,i=1,2,

x≻iy=x↘iy+x↗iy,x≺iy=x↖iy+x↙iy,i=1,2,

x↘12y=x↘1y+x↘2y,x↗12y=x↗1y+x↗2y,

x↖12y=x↖1y+x↖2y,x↙12y=x↙1y+x↙2y,

x∨12y=x∨1y+x∨2y,x∧12y=x∧1y+x∧2y,

x≻12y=x≻1y+x≻2y,x≺12y=x≺1y+x≺2y,

x∗1y=x↘1y+x↗1y+x↖1y+x↙1y,

x∗2y=x↘2y+x↗2y+x↖2y+x↙2y,

x∗12y=x∗1y+x∗2y.

Proposition 3.1[12]Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra.

Then(A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2),(A,↘12,↗12,↖12,↙12)are L-quadri-algebras.If we define

Proposition 3.2For an L-octo-algebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2),define

x◃1y=x∗2y,x▹1y=x∗1y,

x◃2y=x∨12y,x▹2y=x∧12y,

x◃3y=x∨2y−y∧1x,x▹3y=x∧2y−y∨1x,

x◃4y=x≻12y,x▹4y=x≺12y,

x◃5y=x≻2y−y≺1x,x▹5y=x≻1y−y≺2x,

x◃6y=x↘12y−y↖12x,x▹6y=x↗12y−y↙12x.

Then(A,◃i,▹i)(i=1,2,3,4,5,6)are L-dendriform algebras.(A,◃1,▹1)is the associated vertical L-dendriform algebra of(A,∨2,∧2,∧1,∨1)and the associated depth L-dendriform algebra of(A,≻2,≻1,≺1,≺2);(A,◃2,▹2)is the associated depth L-dendriform algebra of(A,∨2,∧2,∧1,∨1)and the associated depth L-dendriform algebra of(A,↘12,↗12,↖12,↙12);(A,◃3,▹3)is the associated horizontal L-dendriform algebra of(A,∨2,∧2,∧1,∨1) and the associated horizontal L-dendriform algebra of(A,◃4,▹4)is the associated vertical L-dendriform algebra of(A,≻2,≻1,≺1,≺2)and the associated vertical L-dendriform algebra of(A,↘12,↗12,↖12,↙12);(A,◃5,▹5)is the associated horizontal L-dendriform algebra of(A,≻2,≻1,≺1,≺2)and the associated vertical L-dendriform algebra of(A,◃6,▹6)is the associated horizontal L-dendriform algebra of(A,↘12,↗12,↖12,↙12)and the associated depth L-dendriform algebra of

Proof.It follows straightly from Propositions 2.3 and 3.1.

Proposition 3.3Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra.

(1)If we define x◦1y=x∗12y,then(A,◦1)is a pre-Lie algebra.It is the horizontal pre-Lie algebra of the L-dendriform algebra(A,◃1,▹1),the horizontal pre-Lie algebra of the L-dendriform algebra(A,◃2,▹2)and the horizontal pre-Lie of(A,◃4,▹4)of the L-octoalgebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2);

(2)If we define x◦2y=x∗2y−y∗1x,then(A,◦2)is a pre-Lie algebra.It is the vertical pre-Lie algebra of the L-dendriform algebra(A,◃1,▹1),the horizontal pre-Lie algebra of the L-dendriform algebra(A,◃3,▹3)and the vertical pre-Lie algebra of the L-dendriform algebra (A,◃5,▹5)of the L-octo-algebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2);

(3)If we define x◦3y=x∨12y−y∧12x,then(A,◦3)is a pre-Lie algebra.It is the vertical pre-Lie algebra of the L-dendriform algebra(A,◃2,▹2),the vertical pre-Lie algebra of the L-dendriform algebra(A,◃3,▹3)and the vertical pre-Lie algebra of the L-dendriform algebra(A,◃6,▹6)of the L-octo-algebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2);

(4)If we define x◦4y=x≻12y−y≺12x,then(A,◦4)is a pre-Lie algebra.It is the vertical pre-Lie algebra of the L-dendriform algebra(A,◃4,▹4),the horizontal pre-Lie algebra of the L-dendriform algebra(A,◃5,▹5)and the horizontal pre-Lie algebra of the L-dendriform algebra(A,◃6,▹6)of the L-octo-algebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2);

(5)Define[x,y]=x∗12y−y∗12x.Then(A,[·,·])is a Lie algebra on the L-octo-algebra (A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2).It is also the Lie algebra of the L-quadri-algebra (A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2),(A,↘12,↗12,↖12,↙12)andProof.It follows straightly from Propositions 2.1,2.2,3.1 and 3.2.

4　Bimodules of L-quadri-algebras

Definition 4.1Let(A,↘,↗,↖,↙)be an L-quadri-algebra and V be a vector space. Let l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙:A→gl(V)be eight linear maps.(l↘,r↘,l↗,r↗,l↖, r↖,l↙,r↙,V)is called a bimodule of(A,↘,↗,↖,↙)if the following fourteen equations hold(for any x,y∈A)

[l↘(x),l↘(y)]=l↘(x∗y)−l↘(y∗x),(4.1)

r↘(x↘y)−r↘(y)r∗(x)=l↘(x)r↘(y)−r↘(y)l∗(x),(4.2)

r↘(y↗x)−r↗(x)r∨(y)=l↗(y)r≻(x)−r↗(x)l∧(y),(4.3)

r↗(x≻y)−r↗(y)r∧(x)=l↘(x)r↗(y)−r↗(y)l∨(x),(4.4)

l↘(x)l↗(y)−l↗(y)l↘(x)=l↗(x∨y)−l↗(y∧x)+l↗(y)l↗(x),(4.5)

r↘(x↖y)−r↖(y)r↘(x)=l↖(x)r∗(y)−r↖(y)l↖(x),(4.6)

r↖(x∗y)−r↖(y)r↖(x)=[l↘(x),r↖(y)],(4.7)

l↘(x)l↖(y)−l↖(x↘y)=l↖(y)l∗(x)−l↖(y↖x),(4.8)

r↗(x≺y)−r↖(y)r↗(x)=l↙(x)r↗(y)+l↙(x)r↖(y)−r↖(y)l↙(x),(4.9)

l↗(x)r≺(y)−r↖(y)l↗(x)=r↙(x∧y)−r↖(y)r↙(x),(4.10)

l↗(x)l≺(y)−l↖(x↗y)=l↙(y)l∧(x)−l↖(y↙x),(4.11)

r↘(x↙y)−r↙(y)r≻(x)=l↙(x)r∨(y)−r↙(y)l≺(x),(4.12)

l↘(x)r↙(y)−r↙(y)l≻(x)=−r↙(y)r≺(x)+r↙(x∨y),(4.13)

l↘(x)l↙(y)−l↙(x≻y)=l↙(y)l∨(x)−l↙(y≺x),(4.14)

where

r∗(x)=r↘(x)+r↗(x)+r↖(x)+r↙(x),l∗(x)=l↘(x)+l↗(x)+l↖(x)+l↙(x),

r≻(x)=r↘(x)+r↗(x),l≻(x)=l↘(x)+l↗(x),r≺(x)=r↖(x)+r↙(x),

l≺(x)=l↖(x)+l↙(x),r∨(x)=r↘(x)+r↙(x),l∨(x)=l↘(x)+l↙(x),

r∧(x)=r↗(x)+r↖(x),l∧(x)=l↗(x)+l↖(x).

In fact,according to the definition of the bimodule of an L-quadri-algebra,we can check straightly that(l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V)is a bimodule of an L-quadri-algebra (A,↘,↗,↖,↙)if and only if the direct sum A⊕V of the underlying vector spaces of A and V is turned into an L-quadri-algebra by defining multiplications in A⊕V by

(x+u)↘(y+v)=x↘y+l↘(x)v+r↘(y)u,

(x+u)↗(y+v)=x↗y+l↗(x)v+r↗(y)u,

(x+u)↖(y+v)=x↖y+l↖(x)v+r↖(y)u,

(x+u)↙(y+v)=x↙y+l↙(x)v+r↙(y)u,

where x,y∈A,u,v∈V.We denote it by A nl↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙V.

Proposition 4.1Let(l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V)be a bimodule of an L-quadrialgebra(A,↘,↗,↖,↙).Thenis a bimodule of(A,↘,↗,↖,↙).

Proof.It can be checked straightly by the definition of the bimodule of L-quadri-algebra.

Proposition 4.2Let(A,↘,↗,↖,↙)be an L-quadri-algebra.Then

Proof.We can check it by the Definition 4.1 and Proposition 4.1.

Proposition 4.3Let A be a vector space with eight bilinear products denoted by↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2:A⊗A→A.Then

(1)(↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2,A)is an L-octo-algebra if and only if(A,∨2,∧2,∧1,∨1)is an L-quadri-algebra and(L↘2,R↙2,L↗2,R↖2,L↗1,R↖1,L↘1,R↙1,A) is a bimodule;

(2)(↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2,A)is an L-octo-algebra if and only if(A,≻2,≻1,≺1,≺2)is an L-quadri-algebra and(L↘2,R↗2,L↘1,R↗1,L↙1,R↖1,L↙2,R↖2,A) is a bimodule;

(3)(↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2,A)is an L-octo-algebra if and only if(A,↘12,↗12,↖12,↙12)is an L-quadri-algebra and(L↘2,R↘1,L↗2,R↗1,L↖2,R↖1,L↙2,R↙1, A)is a bimodule.

Proof.It follows from Definitions 4.1 and 3.1.

Proposition 4.4Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and (A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2),(A,↘12,↗12,↖12,↙12)be the associated L-quadri-algebra.Then

Proof.It follows from Propositions 4.1 and 4.3.

Proposition 4.5Let(l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V)be the bimodule of an L-quadrialgebra(A,↘,↗,↖,↙).Then

(1)(l↘,r↗,l↙,r↖,V)is a bimodule of the associated vertical L-dendriform algebra (A,≻,≺)of(A,↘,↗,↖,↙);

(2)(l↘,r↙,l↗,r↖,V)is a bimodule of the associated depth L-dendriform algebra (A,∨,∧)of(A,↘,↗,↖,↙);

(3)(l↘,−l↖,l↗,−l↙,V)is a bimodule of the associated depth L-dendriform algebra (A,◃,▹)of(A,↘,↗,↖,↙).

Proof.This conclusion can be proved straightly by Definition 4.1.

Corollary 4.1Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra.Then

(1)(L↘2,R↖2,L↘1,R↖1,A)is a bimodule of the associated L-dendriform algebra (A,◃1,▹1);

(2)(L↘2,R↙1,L↗2,R↖1,A)is a bimodule of the associated L-dendriform algebra (A,◃2,▹2);

(3)(L↘2,−L↗1,L↗2,−L↘1,A)is a bimodule of the associated L-dendriform algebra (A,◃3,▹3);

(4)(L↘2,R↗1,L↙2,R↖1,A)is a bimodule of the associated L-dendriform algebra (A,◃4,▹4);

(5)(L↘2,−L↙1,L↘1,−L↙2,A)is a bimodule of the associated L-dendriform algebra (A,◃5,▹5);

(6)(L↘2,−L↖2,L↗2,−L↙2,A)is a bimodule of the associated L-dendriform algebra (A,◃6,▹6).

Proof.It follows from Definition 3.1.

Corollary 4.2Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra.Then

(1)(L↘2,R↖1,A)is a bimodule of the associated pre-Lie algebra(A,◦1);

(2)(L↘2,−L↘1,A)is a bimodule of the associated pre-Lie algebra(A,◦2);

(3)(L↘2,−L↗2,A)is a bimodule of the associated pre-Lie algebra(A,◦3);

(4)(L↘2,−L↙2,A)is a bimodule of the associated pre-Lie algebra(A,◦4);

(5)(L↘2,A)is a representation of the associated Lie algebra(A,[·,·]).

Proof.It follows from Definition 3.1.

5　Construction of L-octo-algebras

Definition 5.1Let(A,↘,↗,↖,↙)be an L-quadri-algebra,(l↘,r↘,l↗,r↗,l↖,r↖, l↙,r↙,V)be a bimodule of(A,↘,↗,↖,↙).A linear map T:V→ A is called an O-operator of(A,↘,↗,↖,↙)associated to(l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V)if T satisfies

In particular,an O-operator of an L-quadri-algebra(A,↘,↗,↖,↙)associated to(L↘, R↘,L↗,R↗,L↖,R↖,L↙,R↙,A)is called a Rota-Baxter operator of weight zero on(A,↘,↗,↖,↙).

Proposition 5.1Let(l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V)be a bimodule of an L-quadrialgebra(A,↘,↗,↖,↙).If T is an O-operator of(A,↘,↗,↖,↙)associated to(l↘, r↘,l↗,r↗,l↖,r↖,l↙,r↙,V),then there exists an L-octo-algebra structure on V defined by

Therefore,there exists an L-quadri-algebra structure on V defined by(3.1)as the associated L-quadri-algebra of(V,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)and T is the homomorphism of L-quadri-algebras.Furthermore,T(V)={T(v)|v∈V}⊆A is an L-quadri subalgebra of(A,↘,↗,↖,↙)and there is an induced L-octo-algebra structure on A given by

Moreover,the corresponding associated L-quadri-algebra structure on T(V)is just the L-quadri-algebra structure of(A,↘,↗,↖,↙)and T is an homomorphism of L-quadrialgebras.

Proof.For any u,v,w∈V,we have

u↘2(v↘2w)−v↘2(u↘2w)=l↘(T(u))l↘(T(v))w−l↘(T(v))l↘(T(u))w.

On the other hand,

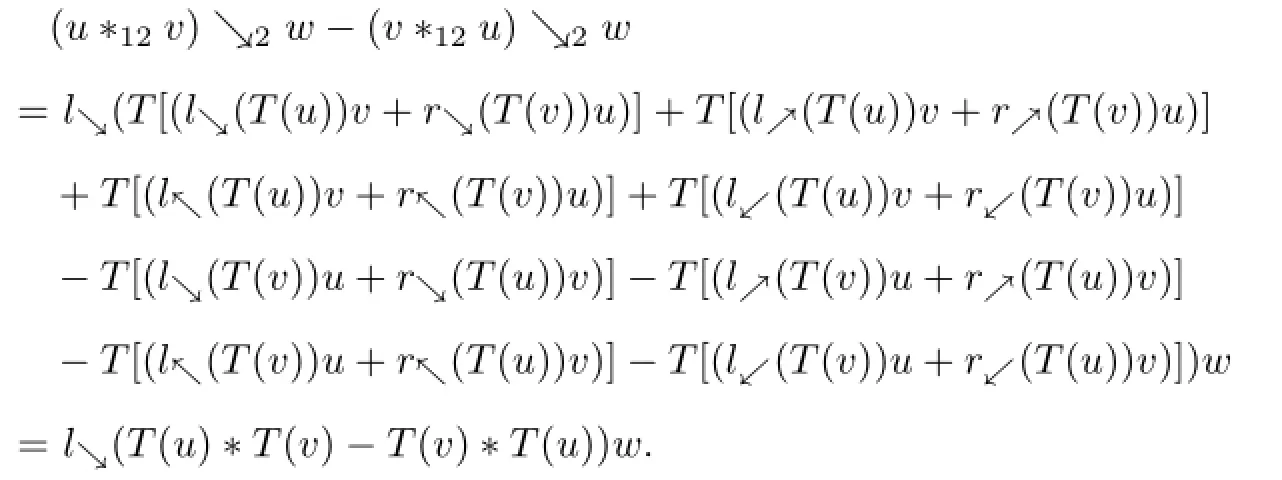
Similarly we can prove the other identities in the definition of L-octo-algebra.The rest of this proposition follows immediately.

Theorem 5.1Let(A,↘,↗,↖,↙)be an L-quadri-algebra.Then there exists an L-octo-algebra structure on A such that(A,↘,↗,↖,↙)is the associated L-octo-algebra if and only if there exists an invertible O-operator of(A,↘,↗,↖,↙).

Proof.Let T be an invertible O-operator of(A,↘,↗,↖,↙)associated to the bimodule (l↘,r↘,l↗,r↗,l↖,r↖,l↙,r↙,V).By Proposition 5.1,there exists an L-octo-algebrastructure on V given by(5.1).Therefore,we define an L-octo-algebra structure on A defined by(5.2)such that T is an isomorphism of L-octo-algebras,that is

Moreover,the associated L-quadri-algebra defined by(3.1)is(A,↘,↗,↖,↙)since

x↘y=T(T−1(x))↘T(T−1(y))=T(l↘(x)T−1(y)+r↘(y)T−1(x))=x↘2y−y↖1x,

x↗y=T(T−1(x))↗T(T−1(y))=T(l↗(x)T−1(y)+r↗(y)T−1(x))=x↗2y−y↙1x,

x↖y=T(T−1(x))↖T(T−1(y))=T(l↖(x)T−1(y)+r↖(y)T−1(x))=x↖2y−y↘1x,

x↙y=T(T−1(x))↙T(T−1(y))=T(l↙(x)T−1(y)+r↙(y)T−1(x))=x↙2y−y↗1x.

Conversely,let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and(A,↘,↗,↖,↙)be the associated L-quadri-algebra(A,◃21,▹21,▹12,◃12).Then the identity map id:A→ A is an invertible O-operator of(A,↘,↗,↖,↙)associated to the bimodule (L↘2,−L↖1,L↗2,−L↙1,L↘2,−L↖1,L↙2,−L↙1,A).

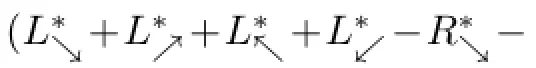
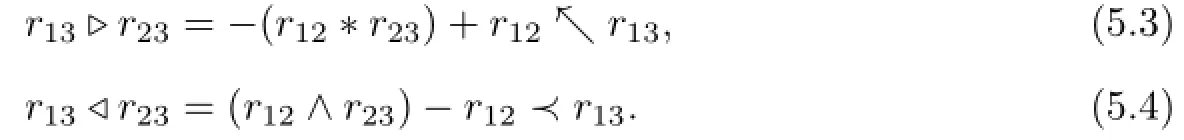
Moreover,if r is invertible,then r satisfies(5.3)–(5.4)if and only if the nondegenerate bilinear form B induced by r satisfies

Proof.Let Fr:A∗→A be the O-operator defined by r.Then

Similarly,by the definition of O-operator,we can get

Let σ be any element in the permutation group Σ3acting on{1,2,3}.Then σ induces a linear map from A⊗A⊗A to A⊗A⊗A by

By the action of Σ and combining these equations we can get the conclusion.

Definition 5.2Let(A,↘,↗,↖,↙)be an L-quadri-algebra and r∈A⊗A be symmetric.(5.3)–(5.4)is called LQ-equation in(A,↘,↗,↖,↙).On the other hand,a symmetric bilinear form B on A satisfying(5.5)–(5.6)is called a 2-cocycle of(A,↘,↗,↖,↙).

Proposition 5.3Let(A,↘,↗,↖,↙)be an L-quadri-algebra with a nondegenerate 2-cocycle B.Then there exists an L-octo-algebra structure(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)on A defined by

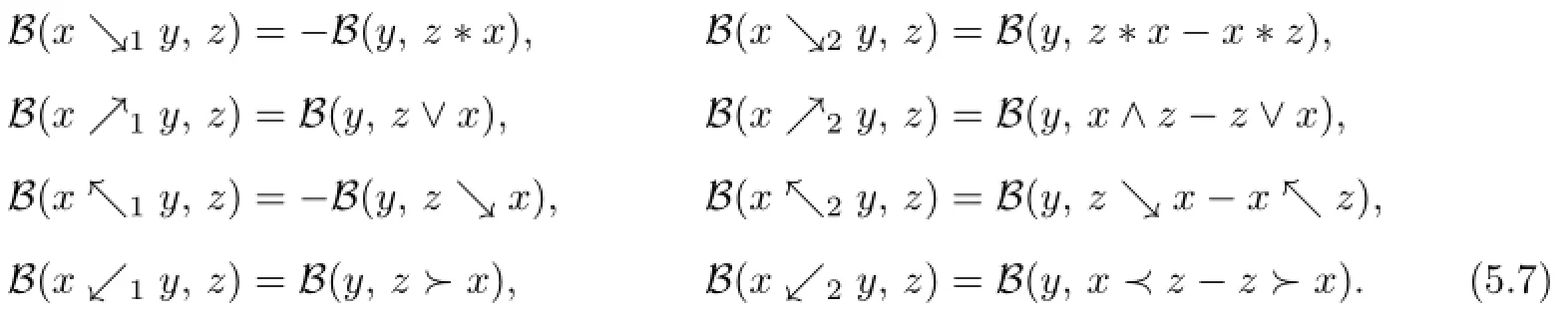
Proof.By Proposition 5.2,the invertible linear map T:A∗→ A is an invertible O-operator associated to the bimoduleAs a result,there is an L-octo-algebra structure on A defined by

Similarly,by a direct computation we can get the other identities in(5.7).

Corollary 5.1Let(A,↘,↗,↖,↙)be an L-quadri-algebra with a nondegenerate 2-cocycle B.Then the corresponding L-quadri-algebra(A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2), (A,↘12,↗12,↖12,↙12)of the L-octo-algebra(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)is given by

Proposition 5.4Let(A,↘,↗,↖,↙)be an L-quadri-algebra and(l↘,r↘,l↗,r↗,l↖, r↖,l↙,r↙,V)be a bimodule.Letbe the bimodule of A.Let T:V→A be a linear map which can be identified as an element in the vector space(A⊕V)⊗(A⊕V).Then r=T−σ(T)is a symmetric solution of LQ-equation in the L-quadrialgebraif and only if T is an O-operator of(A,↘,↗,↖,↙)associate to

Proof.It follows straightly by a direct computation.

Corollary 5.2Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and (A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2),(A,↘12,↗12,↖12,↙12)be the associated L-quadri-algebra.Let{e1,e2,···,en}be a basis of A and{e∗1,e∗2,···,e∗n}be a basis of A∗. Then

is a skew symmetric solution of LD-equation in the L-quadri-algebras

respectively.Moreover,there is a natural 2-cocycle B of this L-quadri-algebras induced by r which is given by

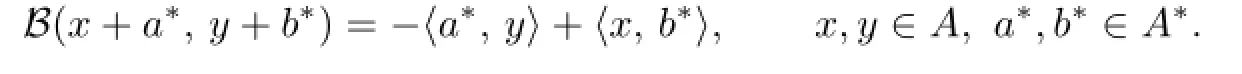
Proof.This is because id is an O-operator of(A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2), (A,↘12,↗12,↖12,↙12).

6　Bilinear Forms on L-octo-algebras and LO-equation

Theorem 6.1Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and r∈A⊗A be skew-symmetric.Let(A,∨2,∧2,∧1,∨1),(A,≻2,≻1,≺1,≺2),(A,↘12,↗12,↖12,↙12)be the associated L-quadri-algebra.Then the following statements are equivalent:

(1)r is the O-operator of(A,∨2,∧2,∧1,∨1)associated to the bimodule

(4)r satisfies

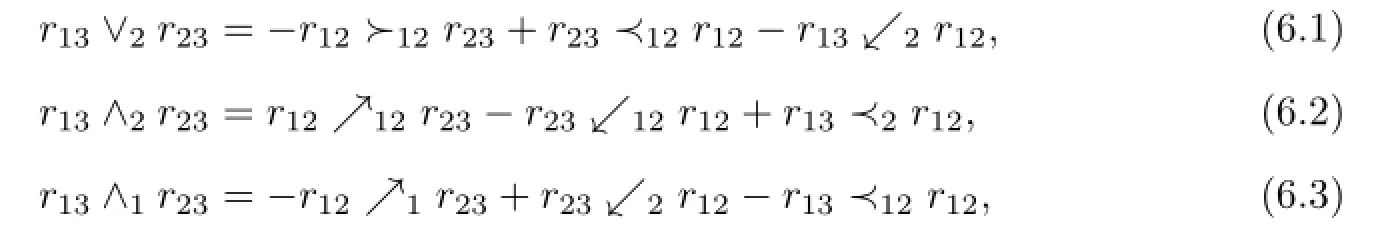
Proof.We just prove the equivalence between(1)and(4).Let{e1,e2,···,en}be a basis of A andbe the dual basis.Suppose that

and

Since r is an O-operator,we have

So we can get

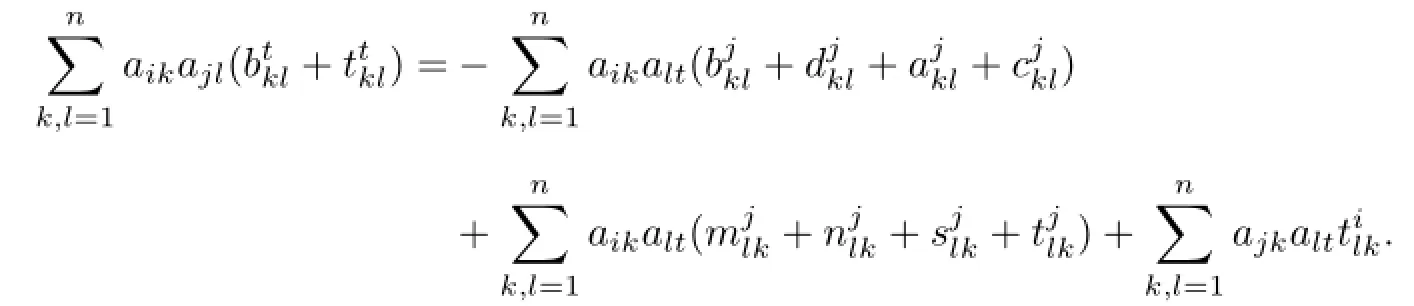
This is the coefficient of ei⊗ej⊗etin

Similarly,we can compute the other identities in(4).Hence this conclusion holds.

Theorem 6.2Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and r∈A⊗A be skew-symmetric.Suppose that r is invertible.Then r satisfies(6.1)–(6.4)if and only if the nondegenerate bilinear form B induced by r satisfies

Similarly,we can compute⟨r13∨2r23,w∗⊗u∗⊗v∗⟩,⟨r12≻12r23,w∗⊗u∗⊗v∗⟩,⟨r23≺12r12, w∗⊗u∗⊗v∗⟩.As a result,we have

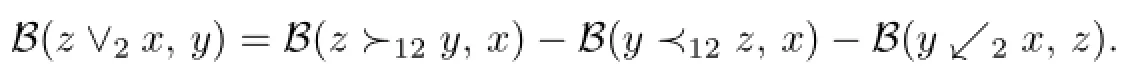
Similarly,we can get the other identities in(6.5)–(6.8).

Definition 6.1Let(A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2)be an L-octo-algebra and r∈A⊗A be skew-symmetric.(6.1)–(6.4)are called LO-equations(a set of equations)in (A,↘1,↘2,↗1,↗2,↖1,↖2,↙1,↙2).On the other hand,a skew symmetric bilinear form B on A is called a 2-cocycle if B satisfies(6.5)–(6.8).

[1]Vallette B.Manin products,Koszul duality,Loday algebras and Deligne conjecture.J.Reine Angew.Math.,2008,620:105–164.

[2]Ebrahimi-Fard K.Loday-type and Rota-Baxter relation.Lett.Math.Phys.,2002,61:139–147.

[3]Loday J L,Ronco M.Trialgebras and Families of Polytopes.in:Homotopy Theory:Relation with Algebraic Geometry,Group Cohomology,and Algebraic K-theory.Contemp.Math.,2004, 346:369–398.

[4]Leroux P.Construction of Nijenhuis operators and dendriform trialgebras.Int.J.Math.Sci., 2004,49:2595–2615.

[5]Leroux P.On some remarkable operads constructed from Rota-Baxter operators.arXiv: math/0311214[math.QA].Submitted on 13 Nov.2013.

[6]Leroux P.Ennea-algebras.J.Algebra,2004,281:287–302.

[7]Loday J L.Dialgebras,in Dialgebras and related operads.Lecture Notes in Math.,2002,1763: 7–66.

[8]Bai C M.A unified algebraic approach to the classical Yang-Baxter equation.J.Phys.A,2007, 40:11073–11082.

[9]Bai C M.Left symmetric bialgebras and an analogy of the classical Yang-Baxter equation. Commun.Contemp.Math.,2008,10:221–260.

[10]Bai C M.O-operators of Loday algebras and annalogues of the classical Yang-Baxter equation. Comm.Algebra,2010,38:4277–4321.

[11]Bai C M,Liu L G,Ni X.Some results on L-dendriform algebras.J.Geom.Phys.,2010,60: 940–950.

[12]Liu L G,Ni X,Bai C M.L-quadri-algebras.Sci.China Ser.A,2011,41(2):105–124.

date:Jan.26,2014.

The NSF(11071106 and 11471151)of China.

E-mail address:finsler@126.com(An H H).