A New Generalized FB Complementarity Function for Symmetric Cone Complementarity Problems

Zhang Yun-sheng and Gao Lei-fu

(College of Science,Liaoning Technical University,Fuxin,Liaoning,123000)

Communicated by Li Yong

A New Generalized FB Complementarity Function for Symmetric Cone Complementarity Problems

Zhang Yun-sheng and Gao Lei-fu∗

(College of Science,Liaoning Technical University,Fuxin,Liaoning,123000)

Communicated by Li Yong

We establish that the generalized Fischer-Burmeister(FB)function and penalized Generalized Fischer-Burmeister(FB)function defined on symmetric cones are complementarity functions(C-functions),in terms of Euclidean Jordan algebras, and the Generalized Fischer-Burmeister complementarity function for the symmetric cone complementarity problem(SCCP).It provides an affirmative answer to the open question by Kum and Lim(Kum S H,Lim Y.Penalized complementarity functions on symmetric cones.J.Glob.Optim..2010,46:475–485)for any positive integer.

complementarity problem,complementarity function,symmetric cone, generalized Fischer-Burmeister function

2010 MR subject classification:90C33

Document code:A

Article ID:1674-5647(2016)01-0039-08

10.13447/j.1674-5647.2016.01.02

1　Introduction

The symmetric cone complementarity problem(SCCP)is defined to find x,y∈V such that

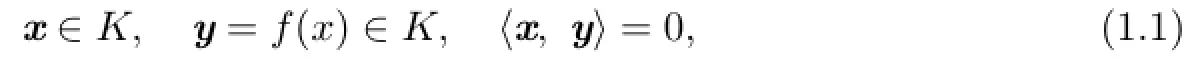
where K is the cone of squares in Euclidean Jordan algebra V,and F:V→V is a continuously differentiable mapping(see[1]–[2]).This class of problem provides a unified framework for the classical nonlinear and complementarity problem(NCP),the second-order cone optimization and complementarity problem(SCOCP),and the semi-definite programming and complementarity problem(SDCP),and has attracted much attention due to its various applications in operations research,economics and engineering.

A popular and powerful approach to solve the complementarity problem is to reformulate each problem as an equivalent system of non-smooth equations by a complementarity function(C-function)(see[3]–[4])or as an unconstrained minimization problem by merit function(M-function)(see[5]).A function ϕ:V×V→V is called a C-function for SCCP if

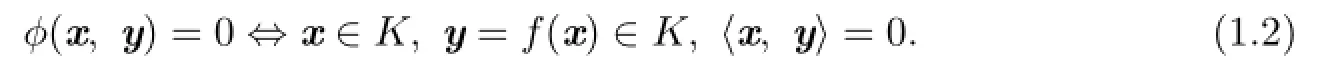
Various C-functions for the standard NCP functions ware extend to the SCCP.For instance, Gowda et al.[6]showed that the Fischer-Burmeister function

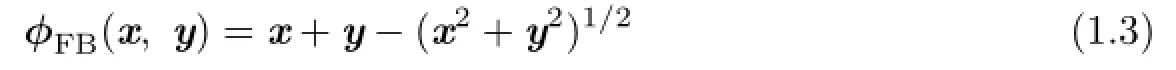
are C-function for any Euclidean Jordan algebra.

A function that can constitute an equivalent unconstrained minimization problem for the SCCP is called an M-function.In other words,a merit function is a function whose global minima is coincident with the solutions of the original SCCP.For constructing an M-function,the C-function severs an important role.

In order to solve(1.1),we only need to find the solution of the nonlinear equations ϕ(x,F(x))=0 induced via the C-function associated with the symmetric cone.Take FB function as a example,the SCCP is equivalent to a system of nonlinear equations:

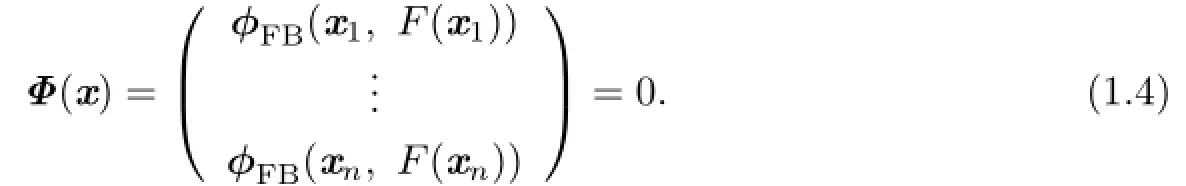
For each C-function,there is a natural merit function ΨFBgiven by

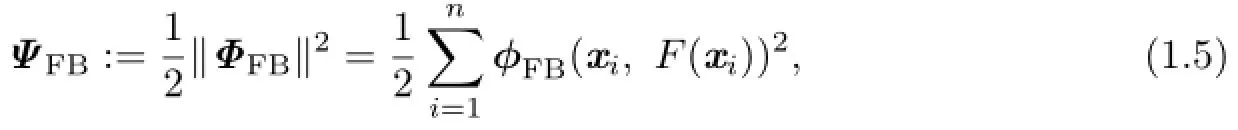
from which the SCCP can be recast as an unconstrained minimization

In this paper,we are particularly interested in the generalized FB,which is presented in a recent paper to deal with NCP by Chen[7]–[8].The definition of the generalized FB function is as follows.

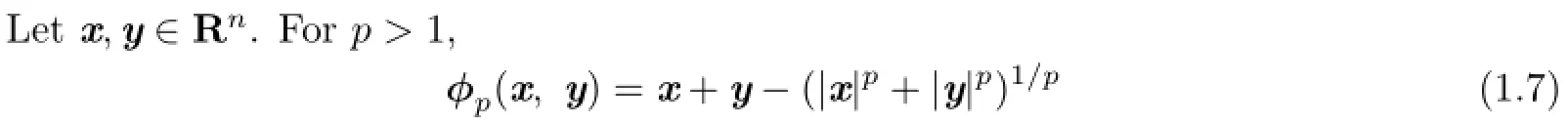
is called the generalized FB function of NCP.

Shortly afterwards,Pan et al.[9]developed the M-function method for SOCCP based on the generalized FB function and Kum et al.[10]proved that generalized FB function and penalized generalized FB function are complementarity functions for SOCCP.Nowadays, Kum[11]extends the generalized FB function to the SCCP when p=1,2,3,4 and proposes a question that“Is the function a C-function for any positive integer n≥2?”Motivated by the above mentioned work,we are trying to extend the generalized FB function to the SCCP when p>1.Moreover,under suitable conditions,we derive the boundedness of level set of the natural M-function induced by the penalized generalized FB function from a trace inequality in Euclidean Jordan algebras,which is very useful toward an entire development of the M-function theory for SCCP based on the penalized version as a future research.

2　Preliminaries

In this section,we mention some concepts and materials of Euclidean Jordan algebras that will be used throughout this paper.For more detailed expositions of Euclidean Jordan algebras,the readers can find in the monograph[12].

A Euclidean Jordan algebra is a triple(V,◦,⟨·,·⟩),where V is a finite-dimensional inner product space over the real field R,and(x,y)7→ x◦y:V×V→ V is a bilinear mapping which satisfies the following conditions:

(1)x◦y=y◦x for all x,y∈V;

(2)x◦(x2◦y)=x2◦(x◦y)for all x,y∈V,where x2:=x◦x;

(3)⟨x◦y,z⟩=⟨x,y◦z⟩for all x,y,z∈V.

We call x◦y the Jordan product of x and y.In addition,we assume that there is an element e,called the unit element,such that x◦e=x for all x∈V.An element c∈V is idempotent if c2=c,and two idempotents c and c′are orthogonal if c◦c′=0.If an idempotent cannot be written by a sum of two non-zero idempotents,then c is called primitive.A complete system of orthogonal idempotents is finite set{c1,c2,···,ck}of idempotents withA complete system of orthogonal primitive idempotents is called a Jordan frame of V.The important spectral decomposition theorems are stated as follows.

Theorem 2.1[12](spectral theorem,first version)For an element of an Euclidean Jordan algebra,there exist unique real numbers λ1(x),λ2(x),···,λk(x)and a unique complete system of orthogonal idempotents{c1,c2,···,ck}such that

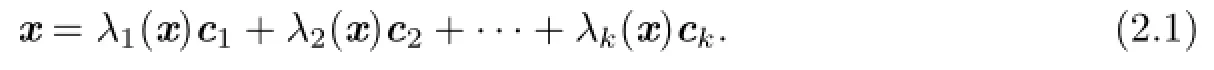
The uniqueness is in the following sense:if there exist a complete system of orthogonal idempotents{e1,e2,···,es}and distinct real numbers η1(x),η2(x),···,ηs(x)such that

x=η1(x)e1+η2(x)e2+···+ηs(x)es,then k=s,ηi=λiand ei=cifor all 1≤i≤k.

Theorem 2.2[12](spectral theorem,second version)Let V be a Euclidean Jordan algebra with rank r.Then for every x∈V,there exist a Jordan frame{c1,c2,···,cr}and real numbers{c1,c2,···,cr}such that

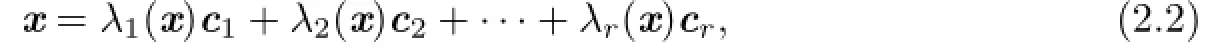
where the numbers λi(x)(i=1,2,···,r)are the eigenvalues of x.

Lemma 2.1Let p be a positive real number.

(1)Each element x≽0 has a unique p-th root denote by x1/pin.If x∈has a spectral decomposition,then

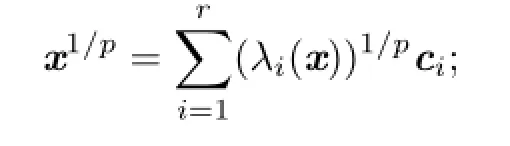
(2)(The L¨owner-Heinz inequality[13])

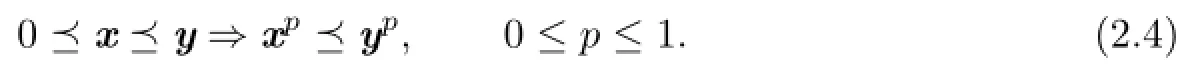
Let g:R→R be a real-valued function.Define the corresponding L¨owner operator G(x): J→J as

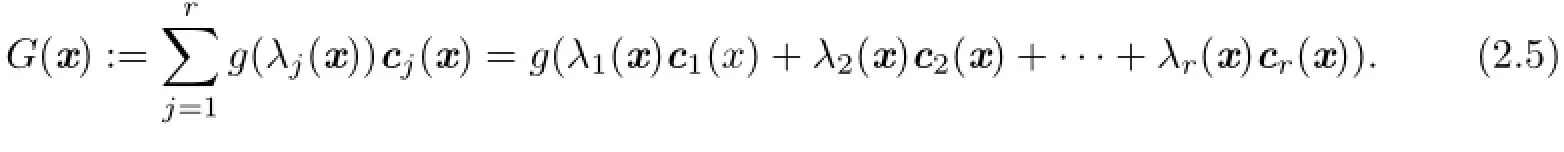
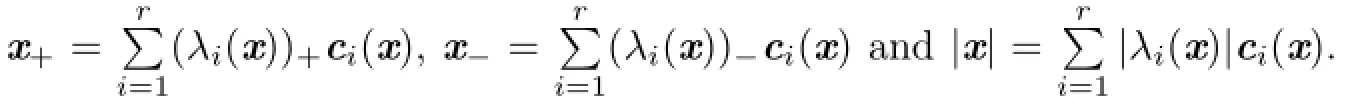
3　The Main Result

In this section,we present two complementarity functions for SCCP.For this purpose,we need to show the following useful proposition.

Proposition 3.1The followings are equivalent:

(1)x,y≽0 and⟨x,y⟩=0;

(2)x,y≽0 and x◦y=0;

(3)x+y=(x2+y2)1/2;

(4)x+y≽0 and x◦y=0;

(5)x,y≽0 and xt◦ys=0 for all nonnegative real numbers s,t.

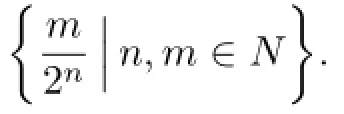
From

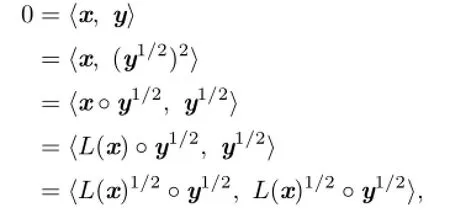
where we used the fact that l(x)is positive semi-definite and hence it has the square root L(x)1/2,we have

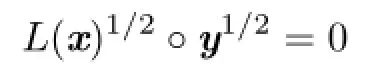
or

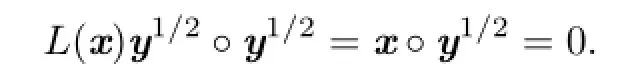
Similarly,

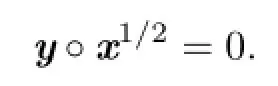
By induction,one has

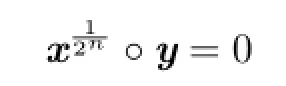
for all positive integers n.

For positive integer m≥2,

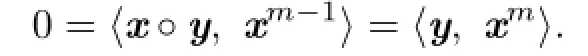
This implies

Therefore,

for all positive integers n and m.

By the density of A in the space of non-negative real numbers,we conclude that

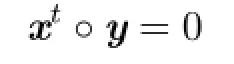
for all nonnegative real numbers t.

Theorem 3.1The function ϕp(x,y):V×V→V defined as(1.7)is a C-function,where V is any Euclidean Jordan algebra.

Proof.First,suppose that x,y≽0 and x◦y=0.It is obvious that x=|x|and y=|y|. For t≥1,we have,by means of Proposition 3.1(5),xty=0 and ytx=0 for all nonnegative real numbers t.This implies by induction that

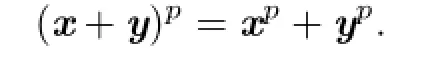
Indeed,letting p>1,one has

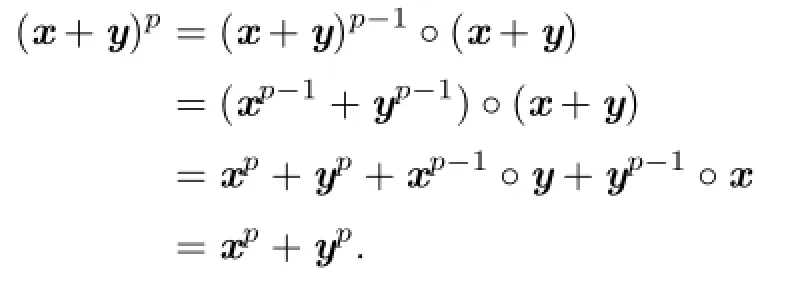
Therefore,

that is,

Second,suppose that

that is,

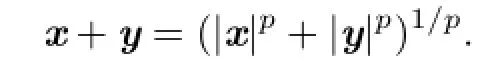
Setting

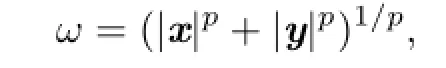
we have

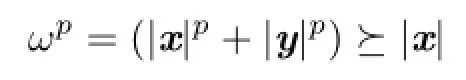
and

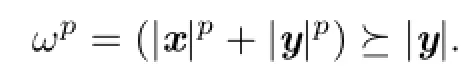
By L¨owner-Heinz inequality,we know that ω≽|x|and ω≽|y|.Since|x|≽x and|y|≽y, we have

Thus,

and so

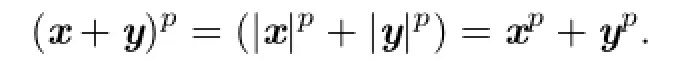
Therefore,

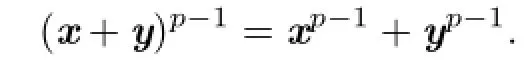
From

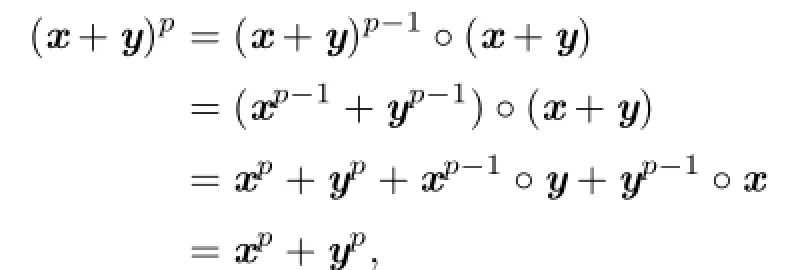
we have

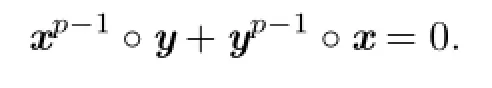
The associative property of the inner product yields

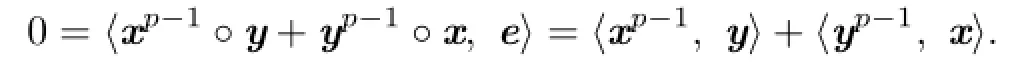
Since x,y≽0,the terms⟨xp−1,y⟩and⟨yp−1,x⟩are non-negative and hence must be zero.It follows from Proposition 3.1 together with its proof that

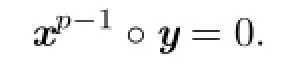
Hence

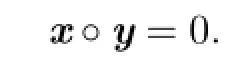
We conclude that ϕp(x,y):V×V→V defined as(1.7)is a C-function.

Similarly,we show that a penalized version of the generalized FB function is also a C-function of SCCP.For p>1 and α>0,define a function as

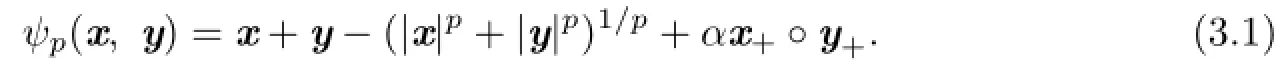
We call ψp(x,y)the penalized version of the generalized FB function.

Theorem 3.2For p>1 and α>0,the penalized version of the generalized FB function

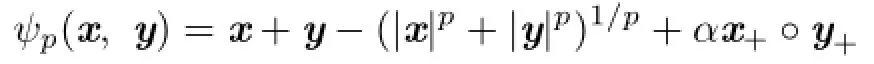
is still a C-function of SCCP.

Proof.First,assume that x,y≽0 and x◦y=0.Then x+=x and y+=y.We have

Hence,from Theorem 3.1,one has

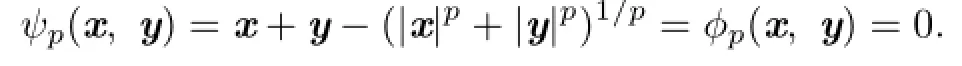
Second,suppose that

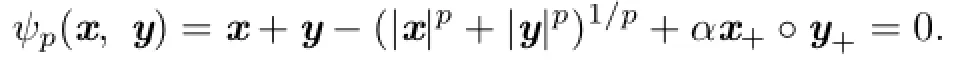
We decompose x as x=x+−x−,where x−=(−x)+.Taking the inner product with−x−, we have

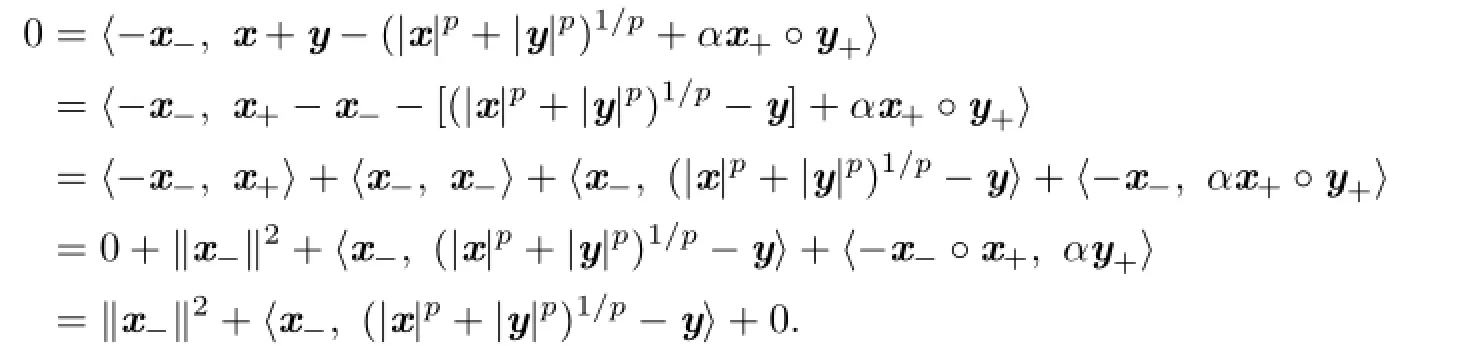
It follows from L¨owner-Heinz inequality that

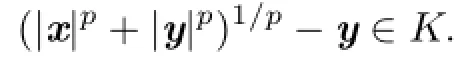
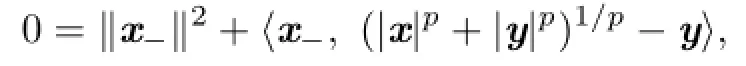
we obtain x−=0.So x≽0.

Similarly,we can get y≽0.

Thus

So we have

that is,

We have

The associative property of the inner product yields

Since x,y≽0,all the terms are non-negative and hence must be zero.It follows from Proposition 3.1(5)together with its proof that xp◦y=0.Hence x◦y=0.

4　Concluding Remarks

In this paper,we extend the generalized FB function to SCCP and introduce a penalized generalized FB function over symmetric.In future research,the next logical step is to analyze semi-smoothness of differentiability of the generalized FB function.

[1]Yoshise A.Complementarity Problems over Symmetric Cone:A Survey of Recent Developments in Several Aspects.New York:Springer-Verlag,2012.

[2]Gowda M S,Sznajder R.Some global uniqueness and solvability results for linear complementarity problems over symmetric cones.SIAM J.Optim.,2007,18(2):461–481.

[3]Huang Z,Ni T.Smoothing algorithms for complementarity problems over symmetric cones. Comput.Optim.Appl.,2009,45:557–579.

[4]Pardalos P M,Maugeri A,Pardalos P M.Equilibrium Problems:Nonsmooth Optimization and Variational Inequality Models.Dordrecht:Kluwer,2002.

[5]Facchinei F,Pang J S.Finite-dimensional Varational Inequalities and Complemebtarity Problems.Volume I,II.Mew York:Springer-Verlag,2003.

[6]Gowda M S,Sznajder R,Tao J.Some P-properties for linear transformations on Euclidean Jordan algebras.Linear Algebra Appl.,2004,393:203–232.

[7]Chen J S.On some NCP-functions based on the generalized Fischer-Burmeister function. Asia-Pac.J.Oper.Res.,2007,24:401–420.

[8]Chen J S,Pan S H.A family of NCP functions and a descent method for the nonlinear complementarity problem.Comput.Optim.Appl.,2008,40:389–404.

[9]Pan S H,Kum S H,Lim Y,Chen J S.On the generalized Fischer-Burmeister merit function for the second-order cone complementarity problem.Math.Comp.,2014,83(287):1143–1171.

[10]Kum S H,Lim Y.Penalized generalized Fischer-Burmeister function for SOCCP.Taiwanese J.Math.,2011,15:1859–1870.

[11]Kum S H,Lim Y.Penalized complementarity functions on symmetric cones.J.Glob.Optim., 2010,46,475–485.

[12]Faraut J,Kor´anyi A.Analysis on Symmetric Cones.Oxford:Clarendon Press,1994.

[13]Lim Y.Applications of geometric means on symmetric cones.Math.Ann.,2001,319:457–468.

[14]Gowda M S,Sznajder R,Tao J.Some P-properties for linear transformations on Euclidean Jordan algebras.Linear Algebra Appl.,2004,393:203–232.

date:Dec.11,2012.

The Specialized Research Fund(20132121110009)for the Doctoral Program of Higher Education.

.

E-mail address:zhangysbad@126.com(Zhang Y S),gaoleifu@163.com(Gao L F).