Triple Crossing Numbers of Graphs
Tanaka Hiroyukiand Teragaito Masakazu
(1.Graduate School of Education,Hiroshima University,1-1-1 Kagamiyama, Higashi-hiroshima 739-8524,Japan)
(2.Department of Mathematics Education,Hiroshima University,1-1-1 Kagamiyama, Higashi-hiroshima 739-8524,Japan)
Communicated by Kawauchi Akio
Triple Crossing Numbers of Graphs
Tanaka Hiroyuki1and Teragaito Masakazu2,*
(1.Graduate School of Education,Hiroshima University,1-1-1 Kagamiyama, Higashi-hiroshima 739-8524,Japan)
(2.Department of Mathematics Education,Hiroshima University,1-1-1 Kagamiyama, Higashi-hiroshima 739-8524,Japan)
Communicated by Kawauchi Akio
We introduce the triple crossing number,a variation of the crossing number,of a graph,which is the minimal number of crossing points in all drawings of the graph with only triple crossings.It is defined to be zero for planar graphs,and to be infinite for non-planar graphs which do not admit a drawing with only triple crossings.In this paper,we determine the triple crossing numbers for all complete multipartite graphs which include all complete graphs.
crossing number,triple crossing number,complete multipartite graph
2010 MR subject classification:05C10
Document code:A
Article ID:1674-5647(2016)01-0001-38
10.13447/j.1674-5647.2016.01.01
1 Introduction
Let G be a graph.A drawing of G means a representation of the graph in the Euclidean plane or the 2-sphere,where vertices are points and edges are simple arcs joining their endvertices.Since each edge is simple,no edge admits self crossings.Furthermore,we assume that the interiors of edges do not contain vertices,and that two edges do not intersect if they have a common vertex,and that two edges without common end-vertex intersect at most once,and if so,then they intersect transversally.These requirements are essential in this paper.A drawing is called a regular drawing(resp.semi-regular drawing)if it has only double(resp.triple)crossing points.From the requirements,we know that a graph has at least 6 vertices if it admits a semi-regular drawing with at least one triple crossing point.
The crossing number cr(G)of G is defined to be the minimal number of crossing points over all regular drawings of G.In particular,cr(G)=0 if G is planar.In this paper,weintroduce a new variation of the crossing number.The triple crossing number tcr(G)is zero if G is planar,and∞ if G does not admit a semi-regular drawing.Otherwise,tcr(G)is defined to be the minimal number of triple crossing points over all semi-regular drawings of G.In particular,tcr(G)=0 if and only if G is planar.
The triple crossing number can be regarded as a specialization of the degenerate crossing number introduced by Pach and T´oth[1].In addition,for example,the Petersen graph is known to have the crossing number two(and thus non-planar),and hence has the triple crossing number one from Fig.1.1.In general,we have the inequality cr(G)≤3tcr(G) for these two notions,since we obtain a regular drawing from a semi-regular drawing by perturbing each triple crossing point into three double crossing points.

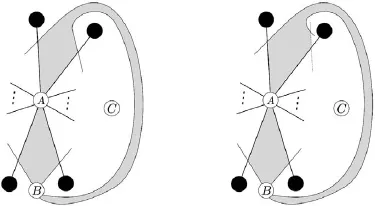
Fig.1.1 The Petersen graph
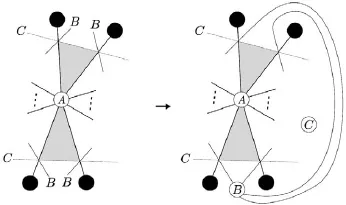
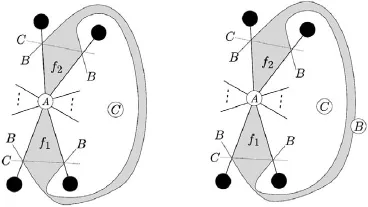
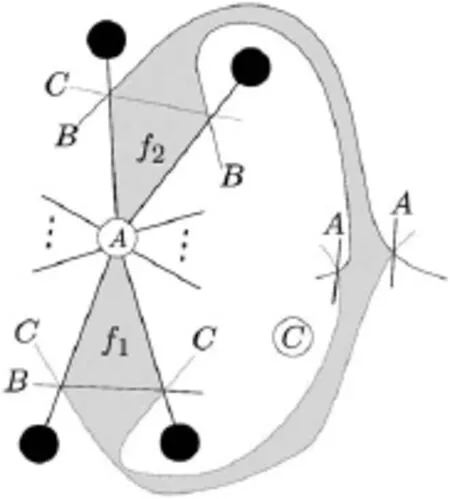
In this paper,we determine the triple crossing numbers for all complete multipartite graphs.A complete multipartite graph is a graph whose vertex set can be partitioned into at least two,mutually disjoint non-empty sets,called the partite sets,so that two vertices u and v are adjacent if and only if u and v belong to different sets of the partition.If the partite sets are of sizes n1,···,nt(ni≥1),then the graph is denoted by Kn1,···,nt.We always assume that ni≥njif i Here is how this paper is organized.After we describe basic lemmas,used in the paper repeatedly,in Section 2,we show that the triple crossing number of a complete t-partite graph is∞if t≥5 in Section 3.In the successive sections,we work on the cases when t≤4. Here we mention that the hardest part is the case where t=2,in particular,long,but elementary,geometric arguments are needed to show that K5,4,K4,4,K5,3and Kn,3with n≥7 do not admit a semi-regular drawing.This is treated in Sections 4,5 and 6.After concluding the case where t=2 in Section 7,the cases where t=4 and t=3 are established in Sections 8 and 9,respectively.Section 10 contains some remarks on our requirements for drawings and a generalization of triple crossing number. Basic terms of graph theory can be found in textbooks such as[2]–[3]. Lemma 2.1The complete bipartite graph K3,3and the complete graph K5with five vertices are non-planar.Also,a graph is non-planar if it contains K3,3or K5as a subgraph. For a graph with p vertices and q edges,let d=3p−q−6. Lemma 2.2Let G be a plane graph with p(≥3)vertices and q edges.Then G has a vertex of degree less than 6 and the inequality d≥0 holds.Furthermore,d=0 if and only if each region of G is 3-sided. For the proofs of these lemmas,see[2]. Lemma 2.3Let G be a graph with p(≥3)vertices and q edges.If G admits a semi-regular drawing,then d≥0.Thus,if d<0,then tcr(G)=∞. Proof.Let D be a semi-regular drawing of G,and let k be the number of triple crossing points in D.If a new vertex is added to each triple crossing point,then we obtain a(simple) plane graph G′.Since G′has p+k vertices and q+3k edges,we have q+3k≤3(p+k)−6 by Lemma 2.2,from which we have the conclusion. Lemma 2.4Let G be a connected plane graph with p(≥3)vertices,q edges and r faces. (1)If d=1,then one face is 4-sided,and the others are 3-sided. (2)If d=2,then either (a)one face is 5-sided,and the others are 3-sided;or (b)two faces are 4-sided,and the others are 3-sided. (3)If d=3,then either (a)one face is 6-sided,and the others are 3-sided;or (b)one face is 5-sided,another face is 4-sided,and the others are 3-sided;or (c)three faces are 4-sided,and the others are 3-sided. Proof.By Euler’s formula(see[2]),p−q+r=2.Let ridenote the number of i-sided faces of G.Then Thus Since q=p+r−2 and d=2p−r−4,we have In particular,the difference between the second and third terms,which is r4+2r5+3r6,is at most d.We remark that d≡r(mod 2). When d∈{1,2,3},4r is the only multiple of four within the interval[4r−d,4r]. Since 4(r3+r4+r5+r6)is a multiple of four,we see 4(r3+r4+r5+r6)=4r,giving r3+r4+r5+r6=r.Furthermore,if r5=r6=0,then(2.1)reduces to 3r3+4r4=2q. Combining this with r3+r4=r gives r4=2q−3r=d. (1)Since r4+2r5+3r6≤d=1,we have r5=r6=0.Then r4=1,and thus r3=r−1. (2)Since r4+2r5+3r6≤2,we have r6=0 and r5≤1.If r5=1,then r4=0,giving r3=r−1.This is the conclusion(a).If r5=0,then r4=2,and thus r3=r−2.This is the conclusion(b). (3)Since r4+2r5+3r6≤3,we have r6≤1.If r6=1,then r4=r5=0,and thus r3=r−1.This is the conclusion(a). Suppose r6=0.Since r4+2r5≤3,we see r5≤1. If r5=1,then r4≤1.From(2.1),3r3+4r4=2q−5.Combining this with r3+r4=r−1 gives r4=2q−3r−2.Since r≡1(mod2),we have r4=1.Hence r4=r5=1 and r3=r−2. This is the conclusion(b). Finally suppose r5=0.Then r4=3,and thus r3=r−3.This is the conclusion(c). Theorem 3.1If G is a complete t-partite graph with t≥5,then G does not admit a semi-regular drawing.Thus,tcr(G)=∞. Proof.Assume for a contradiction that G admits a semi-regular drawing D.Let t≥7.If a new vertex is added to each triple crossing point,then we have a plane graph G′.However, the original vertices have degree at least t−1(≥6),and the new vertices have degree 6. This contradicts Lemma 2.2. Let G=Kn1,n2,···,n6.Then G hasedges.So This contradicts Lemma 2.3. Finally,let G=Kn1,n2,···,n5.As above, This contradicts Lemma 2.3 again. Corollary 3.1Let Knbe the complete graph with n vertices.Then Throughout this section,we assume that G=K5,4admits a semi-regular drawing.We show that this is impossible. Let V1={x1,x2,x3,x4,x5}and V2={A,B,C,D}be the partite sets of G.For convenience,we refer to vertices of V1(resp.V2)as black(resp.white)vertices.We denotethe edge Axiby aifor 1≤i≤5.These are called A-lines.Similarly,define bi,ci,di,and call them B-,C-,D-lines,respectively.In particular,each black vertex is of degree four, and is incident with four distinct classes of lines. We fix a semi-regular drawing of G hereafter,which is denoted by the same symbol G. Notice that any line in G connects a white vertex and a black vertex,and there may be triple crossing points on it.From our requirements for drawings,each triple crossing point of G arises from three distinct classes of lines.This fact will be referred to as property(∗) throughout the paper.Property(∗)is very useful and powerful.For example,if an A-line and a B-line intersect at a triple crossing point,then we can conclude that the remaining line through the triple crossing point is either a C-or D-line. Let k be the number of triple crossing points.Add a new vertex to each triple crossing point.Then we have a plane graph G′with 9+k vertices and 20+3k edges.Since 3(9+k)−(20+3k)−6=1,the faces of the plane graph G′are all 3-sided,except a single 4-sided face by Lemma 2.4.For the semi-regular drawing G,a face means that of G′, although it is an abuse of words.A 3-sided face is also called a triangle. Take a look around vertex A.There are five faces of G,since A is not a cut vertex.We may assume that all five faces around vertex A are triangles without loss of generality,since the 4-sided face is incident with at most two white vertices.There are two types of triangles around vertex A as shown in Fig.4.1.A type I triangle is incident with two triple crossing points,and a type II triangle is incident with a black vertex and a triple crossing point. Fig.4.1 Two types of triangles at A and an adjoint pair of type II triangles Notice that type II triangles appear in pairs.More precisely,this means that every type II triangle at A shares an A-line fully with another type II triangle.Such a pair of type II triangle is referred to as an adjoint pair of type II triangles.See Fig.4.1.Hence the number of type II triangles around vertex A is either 0,2 or 4.We will eliminate these three possibilities. Lemma 4.1The number of type II triangles at vertex A is not four. Proof.Suppose that there are four type II triangles at A.Then we can assume that the local configuration at A is as shown in Fig.4.2(1)by renaming B,C,D,if necessary. (Recall that each black vertex is incident with four distinct classes of lines.) Then,by property(∗),the horizontal line is a B-or D-line,and the right lower line is a C-or D-line.See Fig.4.2(2),where the symbol B/D,for example,indicates the class of thehorizontal line.It does not mean that vertex B or D locates the left side of the horizontal line.Thus there are four cases as shown in Fig.4.3. Fig.4.2 Four type II triangles at A Fig.4.3 Four cases where are four type II triangles The class of the right upper line is determined by property(∗)and the fact that each black vertex is incident with four distinct classes of lines.For Fig.4.3(4),the right upper line may be a C-line.But then,it can be reduced to(3)by renaming B and D and symmetry. Claim 4.1Fig.4.3(1)is impossible. Proof.Consider the B-line b2.Let f1,f2be the faces incident with b2and vertex x2.See Fig.4.4. Fig.4.4 The B-line b2and two faces f1,f2 If f1is 4-sided,then f2is 3-sided,because there is only one 4-sided face.Since two B-lines cannot intersect at a triple crossing point by property(∗),the horizontal B-line and b2meet at vertex B as shown in the second of Fig.4.4 in order to make f23-sided.However, f1cannot be 4-sided.Thus we can conclude that f1is 3-sided.Then vertex B is located around f1as shown in the first of Fig.4.5 by the same reason as above. Fig.4.5 f1is 3-sided Also,then f2cannot be 4-sided,and thus 3-sided.Hence the B-line,intersecting two A-lines a3and a4,turns out to be b1.That is,it goes to black vertex x1as shown in the third of Fig.4.5.(At this point,b1may contain triple crossing points on it after crossing a4.)Consider the face f3,which is adjacent to f1along the B-line b5. If f3is 3-sided,then the B-line b,which must be b3or b4,intersects the A-line a1.Then b can reach neither x3nor x4,because b cannot cross b1or meet a1twice.Therefore,we found that f3is the only 4-sided face.Thus f4is 3-sided.We see that the line going through the upper triple crossing point of f4is either an A-or B-line by property(∗).Since f5is also 3-sided,the B-line b′goes to x3,or crosses the A-line a3.In any case,f6cannot be 3-sided as described in Fig.4.6.This is a contradiction. Fig.4.6 b′goes to x3or crosses a3 Claim 4.2Fig.4.3(2)is impossible. Proof.First,since the horizontal D-line intersects a3,a4,c5,it is either d1or d2from our requirements for drawings.By symmetry,we can assume that f1is 3-sided as in Fig. 4.7.Then vertex D is located around f1.Then the horizontal D-line turns out to be d1. However,neither f2nor f3is 3-sided,which contradicts that there is only one 4-sided face. Fig.4.7 f1is 3-sided Claim 4.3Fig.4.3(3)is impossible. Proof.In Fig.4.8,either f3or f4is 4-sided.(For,if f3is not 4-sided,then it is 3-sided. Then vertex D is located there,which implies that f4is not 3-sided.)Thus both f1and f2are 3-sided.Then the B-line b1is determined.Since f5is 3-sided,the B-line b,which is b3or b4,crosses the A-line a1.Then b can reach neither x3nor x4,a contradiction. Fig.4.8 Both f1and f2are 3-sided Claim 4.4Fig.4.3(4)is impossible. Proof.In Fig.4.9,if f1is not 3-sided,then f2is 3-sided,and then vertex D is located there.But then,f1cannot be 4-sided.Hence f1is 3-sided.Similarly,so is f2.Then the D-line d1is determined.If f3is 3-sided,then the D-line d,which is d3or d4,crosses the A-line a1.Then d cannot reach any black vertex as before.Hence f3is 4-sided.As in the proof of Claim 4.1,examining f4,f5,f6leads to a contradiction. Fig.4.9 Both f1and f2are 3-sided This completes the proof of Lemma 4.1. Lemma 4.2The number of type II triangles at vertex A is not two.Proof.Suppose that there are two type II triangles at A.Then we can assume that the local configuration at A is as shown in Fig.4.10(1),up to renaming.By property(∗),the left upper line is a B-or D-line.Similarly,the right upper line is a C-or D-line.See Fig. 4.10(2).Then there are three cases,up to symmetry and relabeling of vertices,as shown in Fig.4.11,where the class of the horizontal line is determined by property(∗). Fig.4.10 Two type II triangles at A Fig.4.11 Three cases where there are two type II triangles Claim 4.5Fig.4.11(1)is impossible. Proof.First,assume that f1is 4-sided in Fig.4.12.Then the others are all 3-sided.Thus f2and f3,and then f4,f5are determined as in Fig.4.12.(If an A-line goes through the left triple crossing point of f2,then the face sharing a D-line with f2cannot be 3-sided. Similarly for f3.) Fig.4.12 Assume that f1is 4-sided Consider the B-line b.It goes to x2or crosses the A-line a2.Suppose that the former happens.Then f6,···,f9are determined as in Fig.4.13.Moreover,the D-line d5is also determined. Fig.4.13 The case where b goes to x2 Then the C-line c cannot go to x5,since it crosses d5.Hence it crosses the A-line a5. This forces the D-line d to cross the same a5.Then it cannot reach any black vertex,a contradiction.Therefore,b crosses the A-line a2.By the same reason,c crosses a5. Repeating the same argument,we obtain the configuration as shown in Fig.4.14. Fig.4.14 A final contradiction when f1is 4-sided If the B-line b′crosses the A-line a4,then both b′and b′′go to x3,a contradiction.Thus b′goes to x4.Similarly,the C-line c3is determined.See the second of Fig.4.14. Then f1can be incident with neither vertex B nor C.For example,if f1is incident with B,then the left face of f1cannot be 3-sided.Hence f1is incident with two more triple crossing points.Then the upper horizontal line of f1is an A-or D-line by property(∗). From our requirements,it cannot be an A-line.Thus we have the third of Fig.4.14,but then vertex D cannot be located. Next,assume that f1is 3-sided.We see that a D-line goes through the upper triplecrossing point of f1from our requirements and property(∗). By symmetry,we can assume that f2is 3-sided.See Fig.4.15. Fig.4.15 f1is 3-sided If f3is also 3-sided,then the B-line b′′and the C-line c′meet twice,a contradiction. Hence f3turns out to be 4-sided.Also,no A-line is adjacent to f3,because each of the four A-lines a2,···,a5meets b′′′or c′.Thus vertex B is located as in Fig.4.15.Again, examining f4,f5,f6leads to a contradiction as in the proof of Claim 4.1. Claim 4.6Fig.4.11(2)is impossible. Proof.In Fig.4.16,suppose that f1is 4-sided.Then f2is 3-sided,and so vertex D appears there.Then f3is not 3-sided,a contradiction.Hence f1is 3-sided. Fig.4.16 f1is 3-sided If f2is 3-sided,then f3is 4-sided as above.Otherwise,f2is 4-sided.In any case,f4is 3-sided,and vertex C appears.Also,f5and f6are 3-sided.But this is impossible as in the proof of Claim 4.1 again. Claim 4.7Fig.4.11(3)is impossible.Proof.In Fig.4.17,at least two of f1,f2,f3are 3-sided.If f1and f2are 3-sided,then vertex D cannot be located correctly.Similarly for the case where f1and f3are 3-sided. Hence f2and f3are 3-sided.Then the D-line d goes to x2or x3,and another D-line d′goes to x4or x5.But this is impossible. Fig.4.17 f2and f3are 3-sided This completes the proof of Lemma 4.2. Lemma 4.3The number of type II triangles at vertex A is not zero. Proof.Assume that there are no type II triangles at A.Up to symmetry and relabeling of vertices,the local configuration at A can be assumed as in the first of Fig.4.18. Fig.4.18 Five type I triangles at A By symmetry,we can assume that the right hand side does not contain a 4-sided face. More precisely,f1,···,f4are all 3-sided.Thus vertex B is located.Then examining f2,f3, f4,as in the proof of Claim 4.1,leads to a contradiction.(In this case,f3can be incident with x5.Then f4cannot be 3-sided likewise.) Theorem 4.1K5,4does not admit a semi-regular drawing. Proof.This follows from Lemmas 4.1,4.2 and 4.3. Throughout this section,we assume that G=K4,4admits a semi-regular drawing.We will show that this is impossible. Let V1={x1,x2,x3,x4}and V2={A,B,C,D}be the partite sets of G.As in Section 4, we refer to vertices of V1(resp.V2)as black(resp.white)vertices,and use the same notions as A-lines,type I or II triangles,so on.Also,property(∗)holds from our requirements. We fix a semi-regular drawing of G,which is denoted by G again.Let k be the number of triple crossing points.Add a new vertex to each triple crossing point.Then we have a plane graph G′with 8+k vertices and 16+3k edges.Since 3(8+k)−(16+3k)−6=2, either (1)one face of G′is 5-sided,and the others are 3-sided;or (2)two faces of G′are 4-sided,and the others are 3-sided by Lemma 2.4.As in Section 4,a face of G means that of G′. 5.1Case(1) We treat the case where one face of G is 5-sided,and the others are 3-sided.At most two white vertices appear in the 5-sided face.Hence we can assume that four faces at vertex A are all 3-sided.Thus the number of type II triangles at vertex A is either 0,2 or 4.We will eliminate these three possibilities. Lemma 5.1The number of type II triangles at vertex A is not four. Proof.Assume that there are four type II triangles at A.We may assume that the local configuration at A is as shown in Fig.5.1(1),up to renaming.By property(∗),the right upper line is a C-or D-line,and the left upper line is a B-or D-line(see Fig.5.1(2)).Up to symmetry and relabeling,there are two possibilities as shown in Fig.5.2. Fig.5.1 Four type II triangles at A Fig.5.2 Two cases where there are four type II triangles Claim 5.1Fig.5.2(1)is impossible. Proof.By symmetry,we can assume that both f1and f2are 3-sided.Since f1is 3-sided, vertex D is located.Then f2cannot be 3-sided,a contradiction. Claim 5.2Fig.5.2(2)is impossible. Proof.By symmetry,we can assume that f1,f2are 3-sided again.Then the B-line b3meets the C-line c3,a contradiction. This complete the proof of Lemma 5.1. Lemma 5.2The number of type II triangles at vertex A is not two. Proof.Assume that there are two type II triangles at A.As before,we may assume that the local configuration at A is as shown in Fig.5.3(1).By property(∗),the right upper line is a C-or D-line,and the left upper line is a B-or D-line(see Fig.5.3).Up to symmetry and relabeling,there are two possibilities as shown in Fig.5.4. Fig.5.3 Two type II triangles at A Fig.5.4 Two cases where there are two type II triangles Claim 5.3Fig.5.4(1)is impossible. Proof.Assume that f2is not 3-sided.Then f1is 3-sided,and so vertex B is located there. Thus the B-line b2is determined.See the first of Fig.5.5.Another B-line b crosses the A-line a2,but then it cannot reach any black vertex. Fig.5.5 b crosses a2 Hence f2is 3-sided,so vertex D is located.Then f3cannot be 3-sided.Thus f1is 3-sided,so vertex B is located,and the B-line b2is determined again as in the second of Fig.5.5.Examining b leads to a contradiction as above. Claim 5.4Fig.5.4(2)is impossible. Proof.By symmetry,we may assume that both f1and f2are 3-sided.Then vertex B is located.See the first of Fig.5.6. If f3is 3-sided,then the B-line b and the C-line c meet twice,a contradiction.Hence f3is not 3-sided,and b goes to x2as in Fig.5.6.Then a line b′turns out to be a B-line.But this B-line cannot reach any black vertex,otherwise it crosses a2twice. This completes the proof of Lemma 5.2. Fig.5.6 Both f1and f2are 3-sided Lemma 5.3The number of type II triangles at vertex A is not zero. Proof.Assume that there is no type II triangle at A.Up to symmetry and relabeling,there are two possibilities as shown in Fig.5.7. Fig.5.7 Two cases where there are four type I triangles In any case,we can assume that f1is 3-sided by symmetry.Then vertex B is located there.The B-line b goes to x1or x2,and the B-line b′goes to x3or x4.This is impossible. Proposition 5.1Case(1)is impossible. Proof.This immediately follows from Lemmas 5.1,5.2 and 5.3. 5.2Case(2) We treat the case where two faces of G are 4-sided,and the others are 3-sided.There are two subcases: (2-1)All white vertices are incident with a 4-sided face. (2-2)There is a white vertex which is not incident with a 4-sided face. 5.2.1Subcase(2-1) Around each 4-sided face,just two white vertices appear.Hence there is just one 4-sided face around each white vertex.Also,it implies that if a face is incident with two adjacenttriple crossing points or an adjacent pair of a triple crossing point and a black vertex,then it must be 3-sided. In this subcase,then the number of type II triangle at vertex A is 0,1,2 or 3. Lemma 5.4The number of type II triangles at A is not three. Proof.Assume that there are thee type II triangle at A.Up to symmetry and renaming, the situation is as shown in Fig.5.8(1),where f is 4-sided. Fig.5.8 Three type II triangles at A As remarked above,f1is 3-sided.If f is incident with vertex D,then f1is incident with vertex D.This is impossible.Thus f is incident with vertex C.See Fig.5.8(2).Since f2is also 3-sided,the left upper line of f2is a B-line.We have the configuration as in Fig.5.9(1). Fig.5.9 Three type II triangles at A(continued) Then f3is 3-sided,but this forces f4to be neither 3-sided nor 4-sided,a contradiction.See Fig.5.9(2). Lemma 5.5The number of type II triangles at A is not two. Proof.Assume that there are two type II triangles at A.Up to symmetry and renaming, there are two possibilities as shown in Fig.5.10,where f is 4-sided.Notice that f1and f2are 3-sided. For Fig.5.10(1),either vertex C or D appears around f by property(∗).Since f1is 3-sided,the former is impossible.The latter is also impossible,because f2is 3-sided.For Fig.5.10(2),vertex C appears around f by property(∗).Then f1gives a contradiction, again. Lemma 5.6The number of type II triangles at A is not one. Proof.Suppose that there is one type II triangle at A.Up to symmetry and renaming,the configuration is as shown in Fig.5.11,where f is 4-sided. Fig.5.11 One type II triangle at A Notice that f1is 3-sided.If f is incident with vertex C,then f1is incident with C,an impossible.Hence f is incident with vertex D.Thus we have the configuration as in Fig. 5.11.The fact that f2is 3-sided forces f3to be 4-sided.Then f3is incident with vertices C and D,which contradicts the fact that D is incident with only one 4-sided face. Lemma 5.7The number of type II triangles at A is not zero.Proof.Assume that there is no type II triangle at A.Up to symmetry and renaming,there are two possibilities as shown in Fig.5.12,where f is 4-sided. Fig.5.12 Two cases where there is no type II triangle For Fig.5.12(1),f1is 3-sided,so vertex B is located there.Then b goes to x1or x2,and b′goes to x3or x4.This is impossible. For Fig.5.12(2),vertex C appears around f by property(∗).On the other hand,f1is 3-sided.This is impossible. 5.2.2Subcase(2-2) In this subcase,we may assume that vertex A is not incident with a 4-sided face without loss of generality.Thus the number of type II triangles at A is 0,2 or 4. Lemma 5.8The number of type II triangles at A is not four. Proof.Suppose that there are four type II triangles at A.Then there are two possibilities as in Fig.5.2. Claim 5.5Fig.5.2(1)is impossible. Proof.Among the four faces f1,···,f4,at least two are 3-sided.Furthermore,if f1(resp. f3)is 3-sided,then f2(resp.f4)is 4-sided,and vice versa.Up to symmetry,there are three possibilities: (a)f1and f3are 3-sided; (b)f1and f4are 3-sided; (c)f2and f3are 3-sided. In case(a),f2and f4are 4-sided.Thus the others are all 3-sided.See Fig.5.13(1).By examining f5,the left upper line of f4is not an A-line.Since f5and f6are 3-sided,two D-lines d and d′go to x2,or cross,a contradiction. In case(b),f2and f3are 4-sided.By examining d and d′shown in Fig.5.13(2),the same argument as(a)leads to a contradiction. Fig.5.13 For(a)and(b) In case(c),f1and f4are 4-sided.As above,we see that neither f1nor f4is incident with an A-line.See the first of Fig.5.14.Thus we have two B-lines b and b′as shown there. Since f5and f6are 3-sided,vertex B is located as in the second of Fig.5.14.But then f7cannot be 3-sided,a contradiction.Since f5and f6are 3-sided,vertex B is located as in the second of Fig.5.14.But then f7cannot be 3-sided,a contradiction. Fig.5.14 For(c) Claim 5.6Fig.5.2(2)is impossible. Proof.If both f1and f2are 3-sided,then we have a contradiction as in the proof of Claim 5.2.Hence either of f1or f2is 4-sided.Similarly,either f3or f4is 4-sided.Then there aretwo possibilities,up to symmetry: (d)f1and f3are 4-sided; (e)f1and f4are 4-sided. In case(d),f2and f4are 3-sided as in the first of Fig.5.15. Fig.5.15 For(d) By property(∗),the right upper line ℓ of f3is an A-or B-line.If ℓ is an A-line,then it is either a2or a4.But if ℓ is a4,then ℓ meets c1twice,impossible.If ℓ is a2,then ℓ meets b1twice,impossible.Thus ℓ is a B-line.By the same reason,the right lower line of f1is not an A-line,and so a C-line. Thus vertices B and C are located as in the second of Fig.5.15.After locating f5and f6as in the third of Fig.5.15,consider the B-line b and the C-line c.If b crosses the A-line a2,then so does c1through the same triple crossing point on a2.Then f7cannot be 3-sided. Hence b,and then c,go to x2.Then f7and f8cannot be 3-sided simultaneously. In case(e),f2and f3are 3-sided.See Fig.5.16. By the same argument as(d),the right lower line of f1turns out to be a C-line.Similarly, the upper line of f4is a C-line.Since both f1and f4are 4-sided,vertex C is located as in the second of Fig.5.16.Then f5is not 3-sided,a contradiction. This completes the proof of Lemma 5.8. Lemma 5.9The number of type II triangles at A is not two. Proof.Suppose that there are two type II triangles at A.Then the local configuration at A is Fig.5.4(1)or(2). Fig.5.16 For(e) Claim 5.7Fig.5.4(1)is impossible. Proof.We claim that f1is 4-sided.Assume that f1is 3-sided.Then vertex B is located, and the B-line b2is determined as in Fig.5.17. Fig.5.17 The case where f1is 3-sided Suppose further that f2is 4-sided.If vertex D is incident with f2,then f2cannot be 4-sided.Hence f2is incident with two more triple crossing points.Then the fourth line of f2is an A-,B-or C-line by property(∗).However,the existence of b2implies that it is neither an A-nor B-line.Thus the right lower line of f2is a C-line.Then the second of Fig.5.18 is the only possible configuration for f2.But this is impossible,because two linesmeet at most once. Thus we see that f2is 3-sided,so vertex D is located as in Fig.5.18.Then f3is 4-sided, and the D-lines d3and d4,and thus d2,are determined.But,f4can be neither 3-sided nor 4-sided,because the existence of b2disturbs an A-line and a B-line as above.We have thus shown that f1is 4-sided. Fig.5.18 The case where f1is 3-sided(continued) Next,we claim that f2is 4-sided.Assume not.Then vertex D is located,and thus d4is determined.Also,f3is 4-sided.If f3is incident with x2,then the D-line d2is determined, and thus d3cannot be drawn.Hence f3is incident with another triple crossing point as in the first of Fig.5.19,where an A-or C-line goes through.If it is a C-line,then f4cannot be 3-sided.Hence it is an A-line,in particular,a2.See the second of Fig.5.19.Then d2cannot be drawn. Fig.5.19 The case where f2is 3-sided Thus we have specified two 4-sided faces f1and f2. Now,f3is 3-sided.By property(∗),the right lower line of f2is an A-or C-line.See the first of Fig.5.20.If it is an A-line,then it is a2.But this is impossible,because the right upper line of f2already meets a2.Thus the right lower line of f2is a C-line.Furthermore, if f2is incident with x4,then the situation is drawn as in the second of Fig.5.20.Then b2is determined,and thus vertex B is located.However,b1cannot be drawn. Fig.5.20 f1and f2are 4-sided Thus f2is incident with a triple crossing point at its right.See the first of Fig.5.21.By property(∗),an A-or B-line goes through the triple crossing point.But it cannot be an A-line by examining the(3-sided)face right above f2.After locating vertex B,the B-line b2is determined.Then b1cannot be drawn. Fig.5.21 f1and f2are 4-sided(continued) Claim 5.8Fig.5.4(2)is impossible. Proof.We claim that f1and f4are 4-sided.Assume that f1is 3-sided.Then vertex B is located,and then the B-line b2is determined.See the first of Fig.5.22. Suppose further that f2is 4-sided.Then f2is incident with either vertex C,or vertex D,or two more triple crossing points.If f2is incident with vertex C,then c4is determined, and then c1cannot be drawn.If f2is incident with vertex D,then an A-or B-line appears at the triple crossing point where a C-line meets a D-line.But this is impossible by the existence of b2as in the proof of Claim 5.7.If f2is incident with two more triple crossingpoints,then a similar argument to the proof of Claim 5.7 gives a contradiction again(see Fig.5.22).Thus f2is 3-sided. Fig.5.22 The case where f1is 3-sided Then the situation is as in the proof of Claim 5.4,leading to a contradiction.Thus f1is 4-sided.By the same argument,f4is 4-sided.Then f2and f3are 3-sided.But this is impossible,because there are a B-line and C-line meeting twice. This completes the proof of Lemma 5.9. Lemma 5.10The number of type II triangles at A is not zero. Proof.Suppose that there is no type II triangle at A.Then the local configuration at A is Fig.5.7(1)or(2). In Fig.5.7(1),if f1or f2is 3-sided,then we have a contradiction as in the proof of Lemma 5.3.Thus both are 4-sided.By the same reason,f3and f4are 4-sided,a contradiction. In Fig.5.7(2),if f1or f2is 3-sided,then we have a contradiction as above.Hence f1and f2are 4-sided.Thus f3and f4are 3-sided.Then the C-line c meets the D-line d twice, a contradiction. Proposition 5.2Case(2)is impossible. Proof.This follows from Lemmas 5.4–5.10. Theorem 5.1K4,4does not admit a semi-regular drawing. Proof.This follows from Propositions 5.1 and 5.2. Let G=Kn,3with n≥5.In this section,we show that if n≠6 then G does not admit a semi-regular drawing.Hereafter,we assume that n≥5 and n≠6. 6.1Exceptional faces Let V1and V2={A,B,C}be the partite sets of G.As before,we refer to a vertex of V1(resp.V2)as a black(resp.white)vertex.Any black vertex is incident with an A-line, B-line and C-line. Suppose that G admits a semi-regular drawing.Fix such a drawing,denoted by G again. Property(∗)holds.That is,at each triple crossing point,an A-line,a B-line and a C-line meet.Let k be the number of triple crossing points.Add a new vertex to each triple crossing point.Then we have a plane graph G′with n+3+k vertices and 3n+3k edges.Since 3(n+3+k)−(3n+3k)−6=3,the faces of G′are 3-sided,except at most three faces, by Lemma 2.4.We refer to a non-triangular face as an exceptional face.More precisely, Lemma 2.4 claims that either (1)G′has only one exceptional face,which is 6-sided;or (2)G′has just two exceptional faces,which are 5-sided and 4-sided,respectively;or (3)G′has just three exceptional faces,which are 4-sided. As before,a face of G means that of G′.Let N be the number(counted with multiplicities)of white vertices which are incident with exceptional faces.Then 0≤N≤6,because two white vertices are not adjacent in G′.Since a white vertex is not a cut-vertex of G′,a white vertex cannot appear around one exceptional face twice. Lemma 6.1Two exceptional faces are not incident with the same pair of white vertices. Proof.Suppose that two exceptional faces f and f′are incident with white vertices A and B,say.Then both f and f′are 4-sided,or one is 4-sided and the other 5-sided.See Fig. 6.1.Recall that any black vertex is incident with a C-line.Thus,in any case,we cannot place C-lines. Fig.6.1 Two exceptional faces with the same pair of white vertices Recall that there are two types of triangles at a white vertex as shown in Fig.4.1.Let X=B or C.At vertex A,if a type I triangle is bounded by two A-lines and an X-line, then it is said to be of type I-X.See Fig.6.2.Furthermore,a type I-X triangle is said to be good if the face sharing the X-line with the type I-X triangle is 3-sided.Otherwise,it isbad.In particular,a bad type I triangle is adjacent to an exceptional face,which is referred to as its associated exceptional face. Fig.6.2 A type I-B triangle and a type I-C triangle Lemma 6.2Let{X,Y}={B,C}.If there is a good type I-X triangle at vertex A, then there is neither an exceptional face incident with both A and Y,nor another good type I-X triangle at A.In particular,the number of good type I triangles is at most two. Proof.Let f1be a good type I-C triangle at A.Then the face f2sharing the C-line with f1is 3-sided,so vertex B is located there.Suppose that an exceptional face f is incident with vertex A and B.a similar situation to the proof of Lemma 6.1.Hence we cannot place C-lines.The existence of another good type I-C triangle is excluded by a similar argument. See Fig.6.3.Here,we cannot place the C-lines going to the left upper black vertex and the left lower black vertex simultaneously. Fig.6.3 Two good type I-C triangles at A Lemma 6.3Suppose that there is a bad type I triangle f at vertex A.Let g be the associated exceptional face of f.If g is k-sided(4≤k≤6),then g is incident with at most k−4 white vertices. Proof.We may assume that f is a bad type I-B triangle without loss of generality.As shown in the first of Fig.6.2,the boundary of g contains a sequence of a C-line,a triple crossing point,a B-line,a triple crossing point,a C-line. The existence of this sequence forces g to admit at most k−4 white vertices. Lemma 6.4Two bad type I triangles at vertex A cannot have the same associated exceptional face. Proof.Let f1and f2be bad type I triangles at A whose associated exceptional faces coincide.Let g be the common associated exceptional face.When g is 4-or 5-sided,the situation is as shown in Fig.6.4,where labels B and C may be exchanged. Fig.6.4 Two bad type I triangles with the same associated 4-or 5-sided exceptional face Then we cannot place C-lines as before.If g is 6-sided,then the situation is as shown in Fig.6.5.Similarly,we cannot draw C-lines. Fig.6.5 Two bad type I triangles with the same associated 6-sided exceptional face Lemma 6.5Suppose that G satisfies one of the following conditions: (1)G has a 5-sided exceptional face incident with exactly one white vertex and a 4-sided exceptional face incident with at least one white vertex; (2)G has three 4-sided exceptional faces,only one of which is incident with no white vertex. Then there is at most one bad type I triangle at vertex A. Proof.Let fibe a bad type I triangle at A,and let gibe the associated exceptional face for i=1,2.By Lemma 6.3,we have g1=g2.But this contradicts Lemma 6.4. Lemma 6.6There is at most three bad type I triangles at vertex A. Proof.Suppose that there are four bad type I triangles at vertex A.Since G has at most three exceptional faces and each bad type I triangle is adjacent to an exceptional face,there exist two bad type I triangles whose associated exceptional faces coincide,contradicting Lemma 6.4. Recall that an adjoint pair of type II triangles at vertex A is a pair of type II triangles sharing an A-line fully.See Fig.6.6(1). Fig.6.6 Type II triangles at A Lemma 6.7Suppose that G satisfies one of the following conditions: (1)G has a single 6-sided exceptional face,which is incident with all white vertices; (2)G has a 5-sided exceptional face incident with two white vertices and a 4-sided exceptional face incident with a white vertex; (3)G has three 4-sided exceptional faces,each of which is incident with a white vertex. Then there is no adjoint pair of type II triangles at vertex A.Hence,if there is a type II triangle at A,then it shares an A-line fully with an exceptional face(Fig.6.6(2)). Proof.Suppose that there is an adjoint pair of type II triangle at A.Then f,indicated in Fig.6.6(1),is not 3-sided.However,f cannot be an exceptional face from the assumption, a contradiction. Lemma 6.8There is at most one adjoint pairs of type II triangle at vertex A. Proof.As in the proof of Lemma 6.7,each adjoint pair of type II triangles yields an exceptional face.If two such pairs share the same exceptional face,then the exceptional face must be a 6-sided face without a white vertex.The situation is as shown in Fig.6.7. Then we cannot draw C-lines to the left two black vertices from vertex C. Hence the number of adjoint pairs of type II triangles is no greater than the number of exceptional faces.When G has a 6-sided exceptional face,we have the conclusion. Fig.6.7 Two adjoint pairs of type II triangles sharing the same exceptional face Assume that G has at least two,then two or three,exceptional faces.Suppose that there are two adjoint pairs of type II triangle.Then these pairs correspond to distinct exceptional faces as above.In any case,there exists an adjoint pair of type II triangles which yields a 4-sided exceptional face f.Then the situation is as shown in Fig.6.8. Fig.6.8 An adjoint pair of type II triangles adjacent to a 4-sided face This implies that both g and h are exceptional.Another adjoint pair of type II triangles yields one more exceptional face.Thus G would have 4 exceptional faces,a contradiction. Lemma 6.9If n is odd,then each white vertex is incident with an exceptional face,hence N≥3. Proof.Assume that only triangles appear at a white vertex,A,say.Each triangle at A is incident with either a B-line or a C-line.Moreover,such triangles appear alternatively around A.Hence n must be even. Lemma 6.10Suppose that vertex A is incident with only one exceptional face f.If f is 4-sided and incident with two white vertices,then n is even. Proof.We may assume that f is incident with A and B.Then each triangle adjacent to f at A is incident with a C-line.By the same reason as the proof of Lemma 6.9,n is even. 6.2Reduction Lemma 6.11N≠6. Proof.Let N=6.This happens only when G has three 4-sided exceptional faces,each of which is incident with two white vertices.In particular,a face incident with two adjacent triple crossing points is 3-sided.By Lemma 6.1,there is one exceptional face for each pair of A,B,C.We examine the local configuration at vertex A. By Lemmas 6.2 and 6.3,there is no type I triangle.By Lemma 6.7,each type II triangle is adjacent to an exceptional face. If two exceptional faces at A share an A-line,then there are at most two type II triangles. This implies that n≤4,a contradiction.(We remark that this situation can happen when n=4.)Otherwise,there are at most four type II triangles.In fact,both sides of a type II triangle cannot be exceptional faces,because there is only one exceptional(4-sided)face for each pair of A,B,C(see Fig.6.6(2)).Hence there are exactly four type II triangles and two exceptional faces around A,giving n=6,a contradiction. Lemma 6.12N≠5. Proof.Assume N=5.This happens only when G has three 4-sided exceptional faces f1, f2,f3,two of which are incident with two white vertices,the other to one white vertex.By Lemma 6.1,we may assume that f1is incident with A and B,f2is incident with B and C, and f3is incident with B or C. We examine the local configuration at A.By Lemma 6.3,there is no bad type I triangle. Assume that f3is incident with B.By Lemma 6.2,a good type I-C triangle is impossible, and at most one good type I-B triangle is possible.By Lemma 6.7,there are at most two type II triangles,which are adjacent to f1.Hence we have n≤4,a contradiction. The case where f3is incident with C is similar. Lemma 6.13N≠4. Proof.Assume N=4.Then G has at least two exceptional faces. First,suppose that G has a 5-sided face f and a 4-sided face f′.Then both f and f′are incident with two white vertices.We may assume that f are incident with A,B,and f′to B,C.This case is handled by the same argument as in the second paragraph of the proof of Lemma 6.12. Next,suppose that G has three 4-sided faces f1,f2,f3.By Lemma 6.1,there are five possibilities for three exceptional faces as shown in Table 6.1,up to renaming.By Lemmas 6.9 and 6.10,n≥8 in any case. Table 6.1 Five possibilities From(b)to(e),there is neither bad type I triangle(by Lemma 6.3)nor adjoint pair of type II triangle(by Lemma 6.7).Moreover,there are at most two good type I triangles (by Lemma 6.2)and at most two type II triangles(by Lemma 6.7).This gives n≤5,a contradiction. Consider(a).By Lemma 6.2,there is no good type I-C triangle at A,and at most one good type I-B triangle is possible.By Lemma 6.5,there is at most one bad type I triangle. In total,there are at most two type I triangles.By Lemma 6.8,there is at most one adjoint pair of type II triangles,and further at most two type II triangles,which are adjacent to f1, can be possible.Hence we have n≤7,a contradiction. Lemma 6.14N≠3. Proof.Assume N=3.We divide the proof into three cases,according to the set of exceptional faces of G′. Case 1.G has a single 6-sided exceptional face. Let f be the exceptional face.Then each white vertex is incident with f.By Lemmas 6.2 and 6.3,there is no type I triangle.By Lemma 6.7,there are at most two type II triangles adjacent to f.Hence n≤3,a contradiction. Case 2.G has a 5-sided exceptional face and a 4-sided exceptional face. Let f1and f2be the 5-sided,4-sided exceptional faces,respectively.According to white vertices incident with them,there are four possibilities as in Table 6.2,up to renaming. Table 6.2 Four possibilities and triangles at A By Lemmas 6.9 and 6.10,we have n≥8,except case(b). (a)There is neither bad type I triangle(by Lemma 6.3)nor type II triangle(by Lemma 6.7).By Lemma 6.2,there are at most two good type I triangles.So,n≤2,a contradiction. (b)By Lemma 6.7,there are at most two type II triangles,which are incident with f1. There is neither bad type I triangle nor good type I-C triangle.Thus n≤4,a contradiction. (c)There can be a good type I-X triangle at A for X∈{B,C}.Hence there are at most two good type I triangles by Lemma 6.2.By Lemma 6.5,there is at most one bad type I triangle.There is at most one adjoint pair of type II triangles by Lemma 6.8. Claim 6.1A bad type I triangle does not coexist with an adjoint pair of type II triangles. Proof.Suppose that there is an adjoint pair of type II triangles.Then it is adjacent to f1(see Fig.6.6(1)).If there is a bad type I triangle,then its associated exceptional face is also f1by Lemma 6.3.Hence f1is not incident with a white vertex,a contradiction. In any case,we have n≤4,a contradiction. (d)There is no good type I-C triangle.By Lemma 6.5,there is at most one bad type I triangle.Claim 6.1 holds again.There are at most two type II triangles,which are incident with f2,by Lemma 6.8.In any case,we have n≤6,a contradiction. Case 3.G has three 4-sided exceptional faces. Let f1,f2,f3be the exceptional faces.There are five possibilities as in Table 6.3.Again, we have n≥8,except case(e),by Lemmas 6.9 and 6.10. Table 6.3 Five possibilities and triangles at A The number of good type I triangles is at most two,except(b),by Lemma 6.2.For(b), there is no good type I-C triangle by Lemma 6.2.For(c),(d)and(e),there is neither bad type I triangle(by Lemma 6.3)nor adjoint pair of type II triangles(by Lemma 6.7).Thus (c)and(d)are settled as in Table 6.3.For(a)and(b),there is at most one bad type I triangle(by Lemma 6.5)and at most one adjoint pair of type II triangles(by Lemma 6.8). Thus these cases are also settled as in Table 6.3. The remaining case is(e).If there is no type II triangle,then we have n≤3,a contradiction.Otherwise,let g be a type II triangle.Then g is adjacent to the exceptional face f1.We may assume that g is incident with a B-line.Let h be the face sharing this B-line with g.Then h is 3-sided,so vertex C is located there.This implies that f1is incident with A and C,a contradiction. Lemma 6.15N≥3. Proof.Assume N≤2.We can assume that vertex A is not incident with an exceptional face.By Lemma 6.9,n is even,so n≥8.We estimate the number of triangles at A as before.By Lemmas 6.2 and 6.6,there are at most two good type I triangles and at most three bad type I triangles. Since A is not incident with an exceptional face,type II triangles appear as adjoint pairs. By Lemma 6.8,there is at most one adjoint pair of type II triangles.Then we have n≤7, a contradiction. Theorem 6.1Let n≥5 and n≠6.Then Kn,3cannot admit a semi-regular drawing. Proof.By Lemma 6.15,N≥3.However,this is impossible by Lemmas 6.11–6.14. We have already shown that K4,4,K5,4,K5,3and Kn,3with n≥7 do not admit a semiregular drawing in Sections 4,5 and 6. Theorem 7.1Let G=Kn1,n2.If n2≤2,then tcr(G)=0.If n2≥3,then tcr(G)=∞except K3,3,K4,3,K6,3,K6,4.Moreover,tcr(K3,3)=tcr(K4,3)=1,tcr(K6,3)=2 and tcr(K6,4)=4. Proof.If n2≤2,then G is planar,and thus tcr(G)=0.The graph G has p=n1+n2vertices and q=n1n2edges.Then q−3p+6=(n1−3)(n2−3)−3. Hence if n2≥5,or n2=4 and n1≥7,then q−3p+6>0, and thus tcr(G)=∞by Lemma 2.3. Fig.7.1 K3,1,1,1and K4,1,1,1 Fig.7.1(after removing three edges v2v3,v3v4,v4v2)shows that tcr(K3,3)=tcr(K4,3)= 1,since K3,3and K4,3are not planar from Lemma 2.1.Note that tcr(K6,3)≥2,since cr(K6,3)=6(see[4])and 3tcr(K6,3)≥cr(K6,3).Thus we have that tcr(K6,3)=2 from Fig. 7.2(after removing three edges v2v3,v3v4,v4v2). Fig.7.2 K6,1,1,1 Similarly,we have that tcr(K6,4)=4 from the fact cr(K6,4)=12(see[4])and Fig.7.3. Fig.7.3 K6,4 Theorems 4.1,5.1 and 6.1 show that G=Kn1,n2has no semi-regular drawing for (n1,n2)=(4,4),(5,4),(5,3),(n,3)with n≥7. Theorem 8.1Let G=Kn1,n2,n3,n4.Then tcr(G)=∞,except Kn1,1,1,1with n1∈{1,2, 3,4,6}.Also, Hence we have tcr(G)=∞by Lemma 2.3. Consider the case where n2=n3=n4=1.If n1=1 or 2,then G is planar,and thus tcr(G)=0.Suppose n1≥3.Then G is non-planar by Lemma 2.1,because G contains K3,3as a subgraph.Let V be the partite set of G with n1elements,and let v2,v3,v4be the other vertices of G.Notice that if G admits a semi-regular drawing,then no edge of the triangle v2v3v4contains a triple crossing point.By removing the three edges of the triangle from G,we obtain a semi-regular drawing of a complete bipartite graph Kn1,3.However, this is impossible by Theorem 7.1,unless n1=3,4 or 6.Since K3,1,1,1and K4,1,1,1admit a semi-regular drawing with one triple crossing as shown in Fig.7.1,they have triple crossing number one. Finally,K6,1,1,1admits a semi-regular drawing with two triple crossings as shown in Fig. 7.2.Since tcr(K6,3)=2 by Theorem 7.1,tcr(K6,1,1,1)=2. Theorem 9.1Let G=Kn1,n2,n3.Then we have the value of the triple crossing number of G as in Table 9.1. Table 9.1 tcr(Kn1,n2,n3) If n3≥3,then Thus we obtain tcr(G)=∞by Lemma 2.3. Let n3=2.Then If n2≥3,then If n2=2,then except when n1=2.For these cases,tcr(G)=∞ by Lemma 2.3 again.Since K2,2,2is planar,tcr(K2,2,2)=0. Let n3=1.We have If n2≥4,or if n2=3 and n1≥4,then For these cases,tcr(G)=∞.Since K3,3,1is not planar(it contains K3,3as a subgraph) and it admits a semi-regular drawing with one triple crossing as shown in Fig.9.1,we have tcr(K3,3,1)=1. Fig.9.1 K3,3,1 The remaining cases are when n2=1,2.If n2=1 or n1=n2=2,G is planar.Therefore consider the case where n2=2 and n1≥3.Let V1and V2be the partite sets of G with n1and n2elements,respectively,and let v3be the remaining vertex.Assume that G admits a semi-regular drawing.Notice that no edge connecting v3and a vertex of V2contains a triple crossing point,since|V2|=2.Thus we obtain a semi-regular drawing of a complete bipartite graph Kn1,3by removing two edges between v3and V2.Then we have that n1=3,4 or 6 from Theorem 7.1.In either case,G is not planar,since G contains K3,3as a subgraph. Thus we have by Fig.7.1(after removing the edge v2v4).Since tcr(K6,3)=2 by Theorem 7.1,we obtain by Fig.7.2(after removing the edge v2v4). In this paper,we require that two edges intersect at most once,and two edges with a common end-vertex do not intersect.This is one natural standpoint in the study of the crossing number(see[5]–[6]),but this might be so strong that most complete multipartite graphs do not admit semi-regular drawings.If we relax it,then K4,4,for example,admits a semi-regular drawing as shown in Fig.10.1. Fig.10.1 Two edges intersect twice In general,for n≥4,we can define the n-fold crossing number for a graph G to be the minimal number of n-fold crossing points over all drawings with only n-fold crossings.By a similar argument,we can show that Theorem 3.1 holds for the n-fold crossing number. Furthermore,if G is a non-planar complete t-partite graph with t≥3,then we can show that G does not admit a drawing with only n-fold crossings by similar arguments to those of Sections 2,8 and 9.It might be possible to determine the values of this invariant for complete bipartite graphs. [1]Pach J,T´oth G.Degenerating crossing numbers.Discrete Comput.Geom.,2009,41:376–384. [2]Bondy J,Murty U.Graph Theory:Graduate Texts in Mathematics,vol.244.New York: Springer,2008. [3]West D.Introduction to Graph Theory.Upper Saddle River,NJ,USA:Prentice Hall,Inc.,1996. [4]Kleitman D.The crossing number of K5,n.J.Combinatorial Theory,1970,9:315–323. [5]Pach J,T´oth G.Which crossing number is it anyway?J.Combin.Theory Ser.B,2000,80: 225–246. [6]Sz´ekely L A.A successful concept for measuring non-planarity of graphs:the crossing number. Discrete Math.,2004,276:331–352. date:March 9,2010. . E-mail address:teragai@hiroshima-u.ac.jp(Teragaito M).2 Basic Lemmas
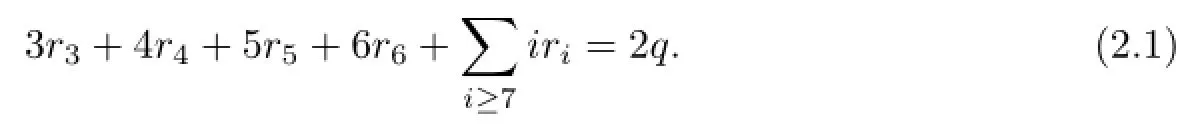


3 Complete t-partite Graphs(t≥5)



4 K5,4




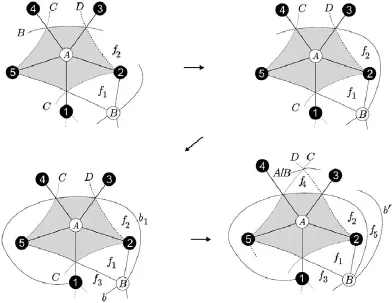






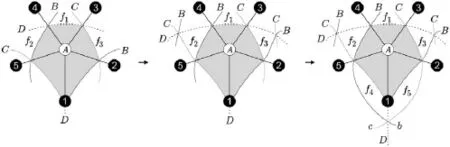


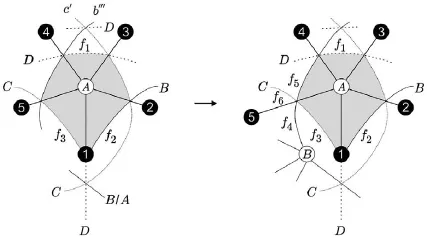
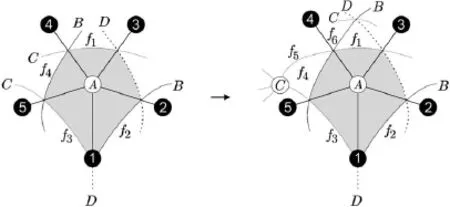
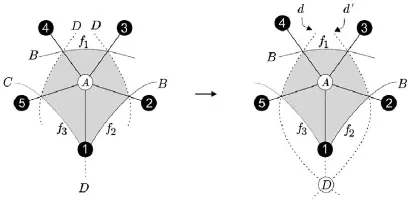

5 K4,4
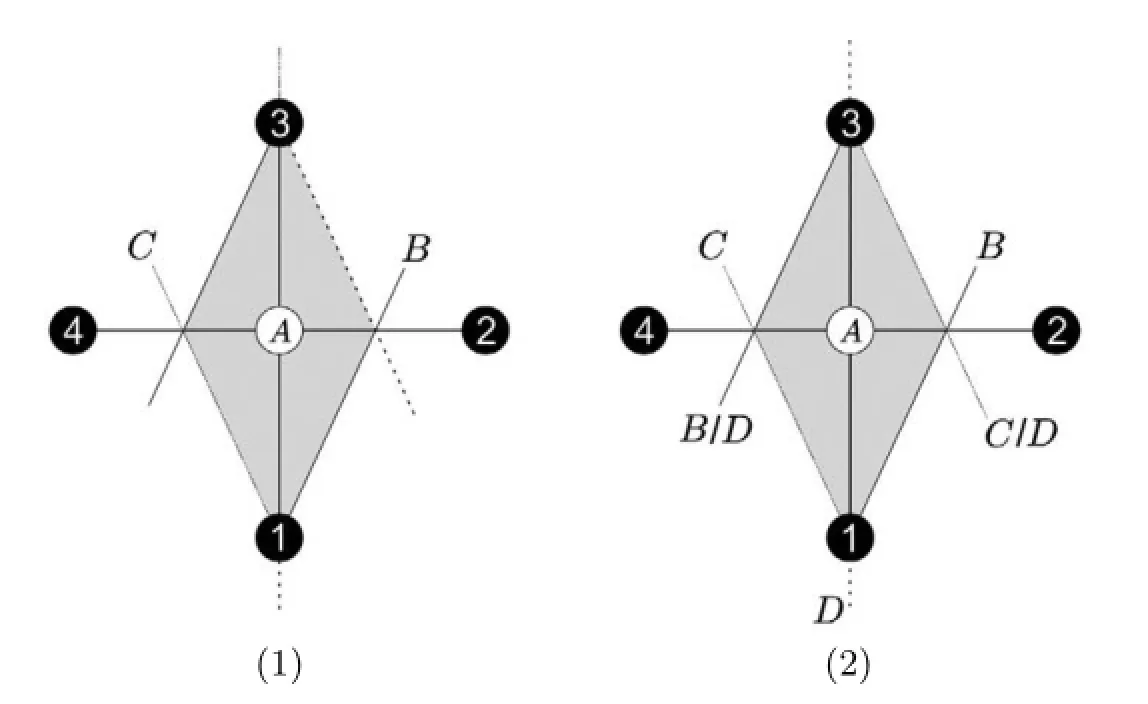
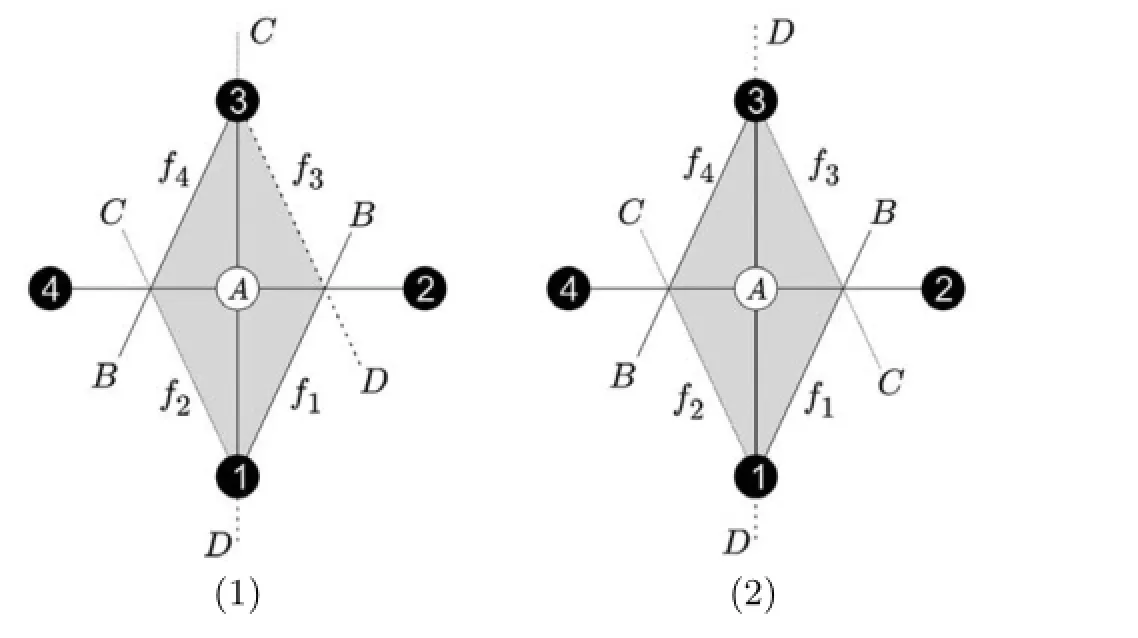



















6 Kn,3







7 Complete Bipartite Graphs


8 Complete 4-partite Graphs


9 Complete Tripartite Graphs

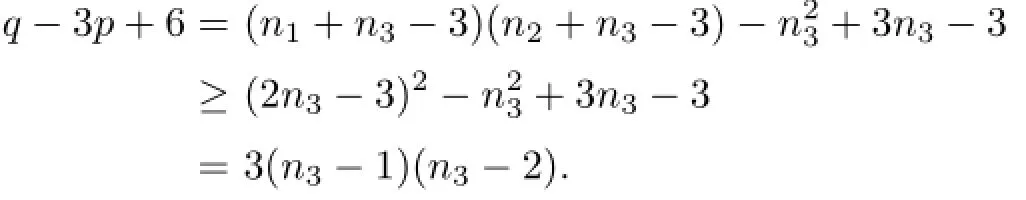



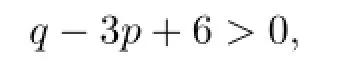



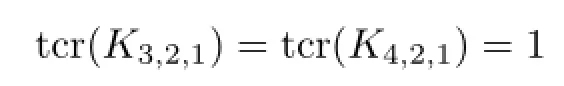

10 Comments
 Communications in Mathematical Research2016年1期
Communications in Mathematical Research2016年1期
- Communications in Mathematical Research的其它文章
- Normality Criteria of Meromorphic Functions
- An Identity with Skew Derivations on Lie Ideals
- Ore Extensions over Weakly 2-primal Rings
- L-octo-algebras
- Normality Criteria of Meromorphic Functions Concerning Shared Analytic Function
- A New Generalized FB Complementarity Function for Symmetric Cone Complementarity Problems
