二量子比特混合态隐形传输保真度研究
崔海生
(重庆邮电大学移通学院 物理系, 重庆 401520)
二量子比特混合态隐形传输保真度研究
崔海生
(重庆邮电大学移通学院 物理系, 重庆401520)
针对二量子比特混合态系统,利用描述态的密度矩阵研究了CHSH违反、混合度与隐形传输保真度的关系。通过共生纠缠度确定了隐形传输保真度的上、下限。结果表明,二量子比特混合态在CHSH违反最大位置或混合度最小位置获得最大隐形传输保真度,并可以通过增加共生纠缠度来提高隐形传输保真度。
CHSH违反; 隐形传输保真度; 混合度; 共生纠缠度
0 引 言
量子光学和信息科学的结合促进了量子信息科学的形成和发展。量子通信、量子计算、量子密码等都是量子信息研究的主要课题。 量子信息的载体是量子态,量子系统的态在演化过程中实现量子信息的处理和传递。在量子态的演化过程中,量子隐形传输保真度是纠缠存在和纠缠强度操作实验的重要基础。它关系到量子通信的失真度,量子计算的可靠性及量子复制的保真度是量子信息学中一个十分重要的问题[1-4]。
纠缠度指所研究的纠缠态携带纠缠的量的多少[5],为不同纠缠态之间建立了可比关系。或者说,纠缠度描述的是共处于同一系统的几个子系的态之间的局域特性,因此只对由几个系统构成的复合系统才有意义,其作为量子信息技术中最宝贵的资源已逐渐应用于量子计算和量子通信中。
近年来,众多学者分别对保真度[1-4]和纠缠度[6-9]开展了广泛的研究,如文献 [1-4]分别研究了高保真度量子存储器以及在克尔媒质中原子和光场的保真度等,文献 [6-9]分别研究了光子频率转换的偏振纠缠保持、耗散纠缠蒸馏等。但对二者的关联研究较少,特别是对二量子比特混合态隐形传输保真度和纠缠度的研究迄今尚未见有文献涉及。
L.Derkacz在文献[10]中对贝尔CHSH不等式和混合度做了具体的研究。文中通过对一类二量子比特混合态的讨论研究了CHSH不等式违反[11]、混合度、隐形传输保真度之间的关系,在此基础上进一步讨论了共生纠缠度与隐形传输保真度之间的关系。首先,考虑一类二量子比特混合态模型,给出它的CHSH违反、混合度、隐形传输保真度。由于深入细致的分析它们之间的关系很困难,于是通过一个具体的二量子比特混合态进行了讨论。
1 贝尔CHSH不等式
C(Concurrence)被认为是测量二量子比特态共生纠缠度的最好方法,定义为[12-13]:
(1)
式中:ρ——密度矩阵;
λmax(ρ)——ρ的最大本征值。
且
式中:ρ*——矩阵ρ的复共扼。

一个任意的二量子比特混合态可以表示为[16]:
(2)
式中:I——二维空间中的单位矩阵;
σ——泡利矩阵;
r,s——实矢量;
Rij——关系矩阵,Rij=tr(ρσi⊗σj)。
定义一个实对称矩阵,U=RTR,它的本征值用λ1,λ2,λ3表示,且λ1≤λ2≤λ3,则CHSH不等式为

(3)
(4)
式中:B——CHSH不等式的贝尔算子;
a,a′,b,b′——单位矢量。
结合方程(2)、(3)、(4),可以得到任意的二量子比特混合态违反CHSH不等式的一种简单表示形式:
令
(5)
则
(6)
当m(ρ)>1,就表示违反CHSH不等式。
2 隐形传输保真度和CHSH不等式
为了研究隐形传输保真度与线性熵和CHSH不等式之间的关系,考虑下面的一类态ε1
(7)
有
(8)
(9)
满足规范条件[17],同时假设
(10)
最近,Bennett等对隐形传输做了研究。在缺少量子信道的情况下,发送者唯一可做的操作是测量未知态,并把测量结果用经典比特告诉给接受者。如果接受者能够重构态,且优于用只建立在经典比特基础上的传输方法,就认为这种态组成的量子信道对传输是有效的[18]。
假如传输一个任意的二量子比特态,通过单重态形成的量子信道发送信息,最后态被忠实地恢复。如果发送方允许在贝尔基上测量,而接受方可用任意的正操作,这种方案叫做标准传输。Horodecki等对标准传输做了研究,并引入隐形传输保真度来度量传输的效率,定义式为[19]
(11)
其中积分遍布统一分布M的布洛菲球的所有的φ·ρk表示得到概率为pk的输出态。Horodecki等同时证明:任意的二量子比特混合态当且仅当

(12)
时对标准传输才是有效的,其中
假设ρ满足条件式(12),则隐形传输保真度可表示为
(13)
对上面态要仔细分析隐形传输保真度F与线性熵SL及CHSH违反之间的关系难度很大,下面通过一个具体的态类来做一些讨论。
考虑一个态
(14)
它满足规范条件。
其中
a+b≤1
且

(15)
于是有
(16)

(17)



得
a+b+c>1
隐形传输保真度为
当a+b=1时,式(16)取得最大值,此时
(18)
(19)
(20)
根据Verstraete and Wolf[20]的结果,对任意的二量子比特混合态,式(18)是当给定共生纠缠度时最大的CHSH违反。那么,对于给定的线性熵和m(ρ),最大的隐形传输保真度是多少?为讨论方便,取SL=S,m(ρ)=m有
(21)
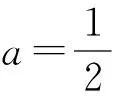
(22)
同理可得F与m的关系为

可以看到,当SL最小时,F最大,即线性熵最小时获得最大的隐形传输保真度;而当m(ρ)最大时,F最大,即最大的CHSH违反对应最大的隐形传输保真度,并且最大的隐形传输保真度相等。
3 隐形传输保真度和共生纠缠度之间的关系
量子纠缠是量子信息过程中至关重要的资源,纠缠最重要的实践特征是量子隐形传输,现在考虑共生纠缠度和隐形传输保真度之间的关系。对于密度矩阵为ρ的二量子比特混合态,隐形传输保真度的上限是
(23)
不等式成立的条件是当且仅当ρ的部分转置矩阵的负本征值对应的本征矢量是最大纠缠的。隐形传输保真度的下限为
(24)
式中:C——共生纠缠度。
所得结果如图1所示。

图1 对于给定的共生纠缠度隐形传输保真度的范围
从图1可以看出,二量子比特混合态可实现的隐形传输保真度大于1/2,但不会超过2/3。共生纠缠度达到1/3以后,隐形传输保真度随其增加较快,说明随着混合态纠缠度的增加,可以通过增加纠缠度来提高隐形传输的保真度。
对于上面讨论过的态类式(14)中,因为C=c,因此上下限的形式和式(21)、(22)相同。特别地,对于二量子比特纯态
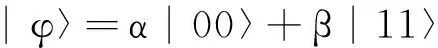
其中α,β≥0,且满足
有
这也说明纯态本质上是混合态的一种特殊情况。
4 结 语
当SL最小时,F最大,即混合度最小时获得最大的隐形传输保真度,而当m(ρ)最大时,F最大,即最大的CHSH违反对应最大的隐形传输保真度,并且最大的隐形传输保真度相等。随着纠缠度的增加,可以通过增加纠缠度来提高隐形传输的保真度。
[1]Yang W L, Yin Z Q, Hu Y, et al. High-fidelity quantum memory using nitrogen-vacancy center ensemble for hybrid quantum computation[J]. Physical Review A,2011,84(1):010301-010304.
[2]Morgan A J, Dalfonso A J, Martin A V, et al. High-fidelity direct coherent diffractive imaging of condensed matte[J]. Physical Review B,2011,84(14):144122-144128.
[3]Stefano Olivare, Matteo G A Paris. Fidelity matters: The birth of entanglement in the mixing of gaussian states[J]. Physical Review Letters,2011,107(17):170505-170509.
[4]吴道永.双光子过程耦合腔系统中光场的量子特性[J].光子学报,2012,41(9):1104-1107.
[5]周正威,郭光灿.量子纠缠态[J].物理,2000,29(11):695-699.
[6]Ramelow S, Fedrizzi A, Poppe A, et al. Polarization-entanglement-conserving frequency conversion of photons[J]. Physical Review A,2012,85(1): 013845-013849.
[7]Karl Gerd H Vollbrecht, Christine A Muschik. Entanglement distillation by dissipation and continuous quantum repeaters[J]. Physical Review Letters,2011,107(12):120502-120506.
[8]廖庆洪,龚黎华.三个两能级原子与数态场相互作用的纠缠特性[J].光子学报,2012,41(3):348-352.
[9]王志,聂敏,刘晓慧.基于纠缠度计算的量子移动信令相邻小区越区切换策略及仿真[J].光子学报,2012,41(4):497-500.
[10]Derkacz L, Jakobczyk L. Bell inequalities versus entanglement and mixedness for a class of two-qubit states[J]. Phys. Lett. A,2004,328:26-35.
[11]Horodecki R. Two-spin-1/2 mixtures and Bell’s inequalities[J]. Phys. Lett. A,1996,210:223-226.
[12]Hill S, Wootters W K. Entanglement of a pair of wuantum bits[J]. Phys. Rev. Lett.,1997,78(26):5022-5025.
[13]Wootters W K. Phys Entanglement of formation of an arbitrary state of two qubits[J]. Phys. Rev. Lett.,1998,80(10):2245-2248.
[14]Von Neumann J. Mathematical foundations of quantum mechanics[M]. Princeton:Princeton University Press,1955.
[15]Bose S. Mixedness and teleportation[J]. Phys. Rev. A,2000,61(4):040101(R)-040102.
[16]Horodecki R, HorodeckiI P, Horodecki M. Violating bell inequality by mixed spin-1/2 states:necessary and sufficient condition[J]. Phys. Lett. A,1995,200:340-344.
[17]Badziag P, Horodecki M. Local environment can enhance fidelity of quantum teleportation[J]. Phys. Rev. A,2000,62(1):012311-012317.
[18]Popescu S. Bell inequallities versus teleportation:What is nonlocality[J]. Phys. Rev. Lett.,1994,72(6):797-799.
[19]Gisin N. Nonlocality criteria for quantum teleportation[J]. Phys. Lett. A,1996,210:157-159.
[20]Wolf M M. Entanglement versus bell violations and their behavior under local filter operations[J]. Phys. Rev. Lett.,2002,89(17):170401-170404.
Study of teleportation fidelity for mixed two-qubit state
CUI Haisheng
(Department of Physics, College Mobile Telecommunications Chongqing University of Posts, Chongqing 401520, China)
To the mixed tow-qubit state system, relationship among CHSH violation, mixedness and the fidelity of teleportation is studied with density matrix. By means of concurrence, the lower and upper bounds of the fidelity of teleportation is determined. Results show that maximum fidelity of teleportation can be obtained when CHSH violation is in maximal position or mixedness is in minimal. In addition, the fidelity of teleportation can be improved by increasing concurrence.
CHSH violation; fidelity of teleportation; mixedness; concurrence.
2016-05-09
崔海生(1979-),男,汉族,山西吕梁人,重庆邮电大学移通学院讲师,硕士,主要从事激光、量子光学和量子信息方向研究,E-mail:hscuiedu@163.com.
10.15923/j.cnki.cn22-1382/t.2016.4.17
O 431.2
A
1674-1374(2016)04-0401-05

