符号大O与符号小o的探究

佘梓航

（韩山师范学院数学与统计学院，广东潮州　521041）

符号大O与符号小o的探究

佘梓航

（韩山师范学院数学与统计学院，广东潮州521041）

文章旨在介绍符号大O及符号小o的定义.通过比较它们的不同，指出学生们在学习大O及小o会遇到的问题，并结合具体的例子探讨如何解决这些问题.

高阶无穷小；同阶无穷小；符号大O；符号小o

1　引言

众所周知，高等数学是理科生重要的必修课程之一，而在高等数学中，极限理论扮演着举足轻重的角色，它是微分学和积分学的基础.学生们学习极限理论的过程当中，他们必然会接触到高阶无穷小量与同阶无穷小量的知识，也因此会接触到符号大O及符号小o（下文将简称为大O小o）.但由于“无穷小的比较”的现有定义有多种表达形式［1］，不同的老师对于“无穷小之比”的理解也不尽相同，这也在无形中导致了学生们对该理论的不理解.本文将先从现有定义对大O及小o进行探讨，指出现有定义存在的不足.介绍现有较为合理的定义［1］.同时，指出学生在学习它们时所遇到的问题，通过适当的例子与说明解决这些问题.

2　大O与小o的定义

大O符号是由德国数论学家Paul Bachmann在1892年著作《解析数论》中首先引入［2］.之后在德国的另一位数学家Edmund Landau的著作中被推广.由此为启发，Edmund Landau在1909年又介绍了小o符号，因此它们有时又称为Landau symbols.从20世纪50年代开始它们被应用于应用数学中的渐近分析.到如今已经被数学家广泛使用，大O符号一般用来刻画被截断的无穷级数，它描述的是函数数量级的渐近上界.小o符号比大O符号需要的条件更强，它代表的是收敛速度更快的函数类.下面将开始对大O及小o进行讨论.

华东师范大学《数学分析》（第四版，上册）［3］中给出如下的定义：

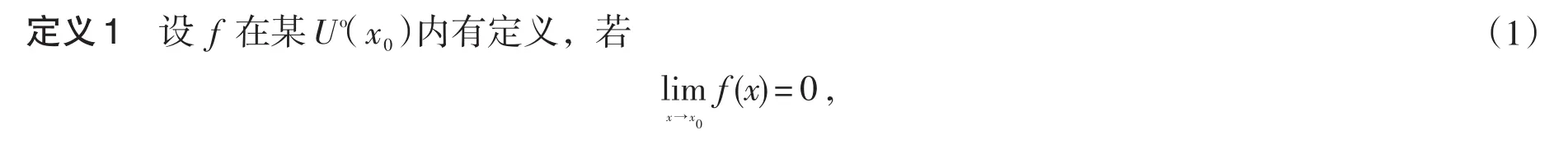
则称f为当x→x0时的无穷小量.

3　学习大O小o会遇到的问题及解答

3.1现有定义的不严谨

首先，从定义本身的内容讲起，上述的定义并不是很严谨.由定义1可以知道，当x→0时，是无穷小量，但是根据定义2并不能比较 f（x）与 f（x）本身的关系.因为只要当x按照数列趋向于0，便会有（无论n多大）.由于分母不能够为0，于是也无法判断f（x）与 f（x）之前的关系（更多例子见文［4］）.但事实上 f（x）与 f（x）是同阶无穷小量，于是必须适当的修改一下该定义，扩大其外延使得可以满足要求.文［1］提出了将无穷小量进行分类，分为第1类无穷小（在Uo（x0）内 f（x）≠0）和第2类无穷小（无论δ多小，必有x1∈Uo（x0）使得 f（x1）=0），同时改进了无穷小的相关定义，解决了该问题.利用文［1］中的定义进行讲解，能够使得学生不会在思考中陷入混乱，从而更好的理解符号大O和小o的含义.

其次，符号小o和大O的定义出现的顺序也容易让学生产生误解.从定义2中可以知道，小o代表的是高阶无穷小量，而在同阶无穷小量的定义出现后立刻出现大O的定义，容易让别人误以为大O便是代表同阶无穷小.其实不然，大O并不等于同阶无穷小.大O的定义中确实包含了同阶无穷小量的定义，大O的适用范围比同阶无穷小的范围大.因此，在教学过程中，可以先讲解大O的定义，再从大O的定义中提炼出同阶无穷小的定义，这样会减少上述问题的发生.

3.2学生学习大O小o时遇到的问题

根据以往的教学经验，大学生们在学习大O小o时容易遇到以下的问题：

问题一：无穷小量中的x是否必须趋向于0？

问题二：小o代表高阶无穷小，是否需要定义高阶无穷大？

问题三：大O和同阶无穷小有什么区别，是否可以只定义大O而不定义同阶无穷小？

问题四：f（x）=O（g（x）（或o（g（x））中的“=”是否代表相等？

问题五：既然大O不是代表同阶无穷小，那么大O与小o是否没有联系？

3.3学生遇到问题的解答

（1）问题一的解答

解答问题一，可以由定义直接解决.定义1～3都是利用Uo（x0）去进行定义，x0是多少并没有规定，也即x0可以是0或者∞，如 f（x）=x-2，在x→2时也是无穷小量.

（2）问题二的解答

在解答问题二之前，必须先解释一下什么是无穷大量？无穷大量简单来讲就是以∞（+∞或-∞）为非正常极限的函数（包括数列）.如在x→0的时候便是无穷大量.其实，高阶无穷大量的概念包含在高阶无穷小量之中.根据定义2，如果存在，称 f（x）为g（x）的高阶无穷小量.假设在某个Uo（x0）内， f（x）≠0，于是，上述的极限可以改为，也即说明了当 f（x）为g（x）的高阶无穷小量时，g（x）则为f（x）的高阶无穷大量，所以并不需要再定义高阶无穷大量.

（3）问题三的解答

在3.1中已经阐明了大O和同阶无穷小的关系.从定义中也可以知道，对于x∈Uo（x0），大O的使用必须满足，，M≥0；而同阶无穷小必须满足，其中K,L＞0.它们最大的不同在于可否为0.下面将通过一个例子来说明它们之间的不同.

例1当x→0时， f（x）=x2+x，g（x）=x2，z（x）=x，试说明 f（x），g（x），z（x）之前的关系.

解：当x→0时，g（x）=O（f（x），此时g（x）却为 f（x）的高阶无穷小量；

但是对于f（x）和z（x），f（x）=O（z（x），此时f（x）也是z（x）的同阶无穷小量.

因此，由上述例1可以知道，大O和同阶无穷小是不同的.如果 f（x）中包含有多项，大O强调的是在x→x0中影响最大的项，而同阶无穷小量强调的是相同的收敛速度.大O在计算数学和计算科学方面用得非常的多，因此，不能只定义大O或同阶无穷小的任意一个.

（4）问题四的解答

f（x）=O（g（x）（或o（g（x））中的“=”并不代表相等，是表示属于的意思.其实

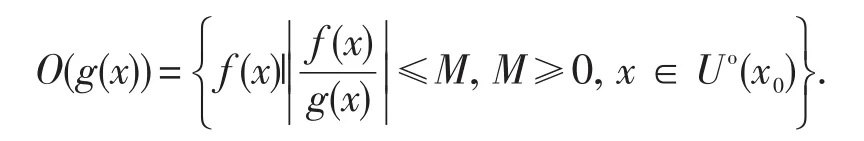
因此，

也正由于O（g（x）和o（g（x）都是代表满足条件的某类函数，因此大O和小o所代表的都是一种定性的关系.对于定量与定性的关系，文［5］通过泰勒公式的余项，对定性与定量进行了说明，同样也能够对问题四进行回答.

（5）问题五的解答

大O和小o之间肯定是有联系的.其实，根据定义1～2，对任意的ε＞0，存在δ＞0，当

4　总结

在符号大O与符号小o的学习中，虽然学生们会遇到各种各样的问题.但是只要牢牢把握住它们的定义，通过适当的例子去进行比较，便可以清楚的区分高阶无穷小、同阶无穷小以及大O与小o的区别.另一个方面，对于数学专业的老师，必须加强在课堂教学中理论联系实际的能力，通过现实生活中应用到的例子进行讲解，这样能够让学生更好的理解.下面举出例子可以供学生在课堂上讨论，以便更好的区分大O与小o.

例2［6］已知当x→a时， f（x）＞0.证明：

（a）o（o（f（x））=o（f（x）；（b）O（o（f（x））=o（f（x）；

（c）o（o（f（x））=o（f（x）；（d）o（f（x）+O（f（x）=O（f（x））

特别的，对于统计专业的学生，在概率论的学习中还将会遇到大OP以及小oP，下标P表示依概率收敛（见文［7］）.它们会在大数定理和中心极限定理的证明中发挥重要的作用，同样，在现在较为前沿的统计研究中也经常用到符号OP及符号oP进行证明，如：股票的协波动率估计量.因此，统计专业的老师也可以适当的给学生们讲解符号OP及符号oP在热门问题中的应用，从而达到既让学生掌握符号大O与符号小o所代表的含义、又培养学生科研能力的效果.

［1］潘建辉，邓志颖，杨春德.“无穷小的比较”的定义及其改进［J］.大学数学，2011，27（3）：204-208.

［2］WIKIPEDIA.Big O notation［EB/OL］.（2015-11-29）［2015-11-30］.https：//en.wikipedia.org/wiki/Big_O_notation.

［3］华东师范大学数学系.数学分析（第四版，上册）［M］.北京：高等教育出版社，2010：60-64.

［4］龚冬保.高阶无穷小与低阶无穷小——无穷小比较的一个问题［J］.高等数学研究，2000，3（3）：16.

［5］许绍元.泰勒公式的余项的定性与定量形式——谈谈在大学数学教学中如何培养学生的创新能力［J］.韩山师范学院学报，2014，35（3）：73-77.

［6］吉米诺维奇，李荣涷.数学分析习题集［M］.李植，译.北京：高等教育出版社，2010：47-48.

［7］茆诗松，程依明，濮晓龙.概率论与数理统计教程（第二版）［M］.北京：高等教育出版社，2011：208-215.

The Discussion of BigONotation and SmalloNotation

SHE Zi-hang
（Shool of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

The aim of this paper is to introduce the definitions of the bigOnotation and the smallonotation.Their differences are compared to show some of the problems which the students encountered in learning bigOnotation and smallonotation.Solutions are discussed by using some examples.

infinitesimal of higher order；infinitesimal of the same order；bigOnotation；smallo notation

G 64；O 17

A

1007-6883（2016）03-0019-04

责任编辑朱本华

2015-12-02

佘梓航（1989-），男，广东潮州人，韩山师范学院数学与统计学院助教.