不规则波作用下垂直挡板式透空堤透浪系数试验研究

邵 杰，陈国平，严士常，杨 嵚

(1.浙江省水利河口研究院 浙江省河口海岸重点实验室，浙江 杭州 310020；2.河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098；3.江苏省交通规划设计院股份有限公司，江苏 南京 210014)

不规则波作用下垂直挡板式透空堤透浪系数试验研究

邵 杰1，陈国平2，严士常2，杨 嵚3

(1.浙江省水利河口研究院 浙江省河口海岸重点实验室，浙江 杭州 310020；2.河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098；3.江苏省交通规划设计院股份有限公司，江苏 南京 210014)

垂直挡板式透空堤作为一种新型的透空式防波堤结构，通过将挡浪板垂直设置于波能最集中的水体表层来消减波浪，透浪系数是其最关键的指标。通过物理模型试验，分析不规则波作用下入射波高、波周期、挡板相对入水深度、相对堤宽、相对挡板超高、相对面板超高等因素对垂直挡板式透空堤透浪系数的影响规律，并在Wiegel公式的基础上拟合了垂直挡板式透空堤透浪系数的计算公式。可作为今后类似透空式防波堤结构透浪系数的近似估算，具有一定的参考价值。

不规则波；垂直挡板；透空堤；透浪系数；防堤波

Abstract:Vertical baffle permeable breakwater is a new style of permeable breakwater structure,which reduces wave height by vertically setting the baffle in the water surface which concentrates most of the wave energy,and the wave-permeating coefficient is the most crucial index.The influence factors of the wave-permeating coefficient of the vertical baffle permeable breakwater under irregular waves are analysised through the physical model experiment,which considers the incident wave height,the wave period,the relative immersed depth of the baffle,the relative width of the breakwater,the superelevation of the baffle,the superelevation of the deck,etc.The formula for calculating the wave-permeating coefficient is obtained on the basis of the formula of Weigel,which can be used as an approximate estimation for the wave-permeating coefficient of similar permeable breakwaters in the future.

Keywords:irregular waves; vertical baffle; permeable breakwater; wave-permeating coefficient; breakwater

垂直挡板式透空堤作为一种新型的透空式防波堤结构，通过将挡板垂直设置于波能最集中的水体表层来消减波浪，不仅减轻了结构自重，而且节省了材料又利于港内外水沙在下部空间的自由交换，可以有效防止港内淤积。近年来，随着防波堤施工技术的迅速发展、波浪理论的逐步成熟和人类对海洋环境的日趋重视，垂直挡板式透空堤已在国内外的一些渔港工程中得以成功实施，并具有十分广阔的应用前景。

透浪系数系指堤后透射波高与堤前入射波高的比值，是透空式防波堤最关键的指标，可用来评估其消浪效果的优劣。国外学者主要对挡板式透空结构的透浪系数进行了理论推导，1947年Ursell[1]首先研究了无限水深下垂直挡浪板的透浪系数，给出了深水直立薄板的精确解；1960年Wiegel[2]在Ursell的基础上，不考虑挡浪板反射，利用波能流守恒，由微幅波理论推导出有限水深情况下透浪系数的近似解析解；1996年Kriebel等[3]在Wiegel理论公式的基础上，考虑挡浪板产生的反射，推导出透浪系数的另一近似解析解；前苏联拉帕教授通过试验推导出透浪系数的经验公式，并被我国《防波堤设计与施工规范》[4]采纳。国内学者对透空式防波堤的透浪系数也开展了一些试验研究，麻志雄[5]对上海吴淞口炮台湾船舶基地高桩承台透空堤断面进行了透浪系数的试验研究；严以新等[6]对福建黄岐渔港多层挡板桩基透空式防波堤进行了消浪机理分析和试验研究；钟瑚穗等[7]通过试验研究，分析了小间距直桩式、栅栏式和直立挡板式三种不同型式桩基透空堤的特点及其透空率与透浪系数间的关系。

虽然国内外已有一些关于透空式防波堤透浪系数的研究成果，但透浪系数的理论公式与试验结果始终未能有机结合，各家关于透浪系数的计算方法也因物理因子不全、适用条件有限、透空堤结构型式各异等原因至今难以推广。考虑到波浪与透空式防波堤相互作用的机理极其复杂，在理论研究难以深入的情形下，针对垂直挡板式透空堤这一新型的透空式防波堤结构，开展不规则波作用下透浪系数的试验研究则显得十分必要，具有重要的实用价值。

1 物理模型设计

试验在波浪水槽(长80 m、宽1.0 m、高1.2 m)内进行，首端安装液压式推板造波机可生成不规则波，末端设有消能缓坡以减少波浪反射。水槽纵向分为两部分，外侧0.5m宽度内用于布设透空堤断面，内侧则用于消除波浪的二次反射。

透空堤的物理模型用有机玻璃制作，面板厚0.02 m，纵梁宽0.02 m、高0.03 m，横梁宽0.03 m、高0.05 m，纵梁搭接在横梁上且与上横梁等高布置。通过连接杆，将透空堤面板水平悬吊，连接杆上部固定于水槽顶部的支架上。垂直挡板的入水深度和面板的高度通过机械装置进行调节。试验暂不考虑桩基的影响，面板顶部与挡板顶部按等高布置。堤前布设3根波高仪用以测量反射波高，堤后布设7根波高仪(每两根间隔1 m)用以测量堤后波高，模型及波高仪布置情况如图1所示。

试验水深d=0.5 m保持不变，其余的物理参数为：入射波的有效波高Hs=0.06 m、0.08 m、0.10 m、0.12 m；有效周期Ts=1.0 s、1.3 s、1.6 s、1.9 s、2.2 s；挡板入水深度t=0.1 m、0.2 m、0.3 m、0.4 m；堤宽B=0.3 m、0.4 m、0.5 m、0.6 m；挡板超高(挡板顶部到静水面的距离)△h=0.035 m、0.075 m、0.095 m；面板超高(面板底部到静水面的距离)△h′=0.015 m、0.055 m、0.075 m。垂直挡板式透空堤断面及上述各物理参数的定义如图2所示。

图1 模型及波高仪布置示意Fig.1 Sketch of the model and the wave-height gauges

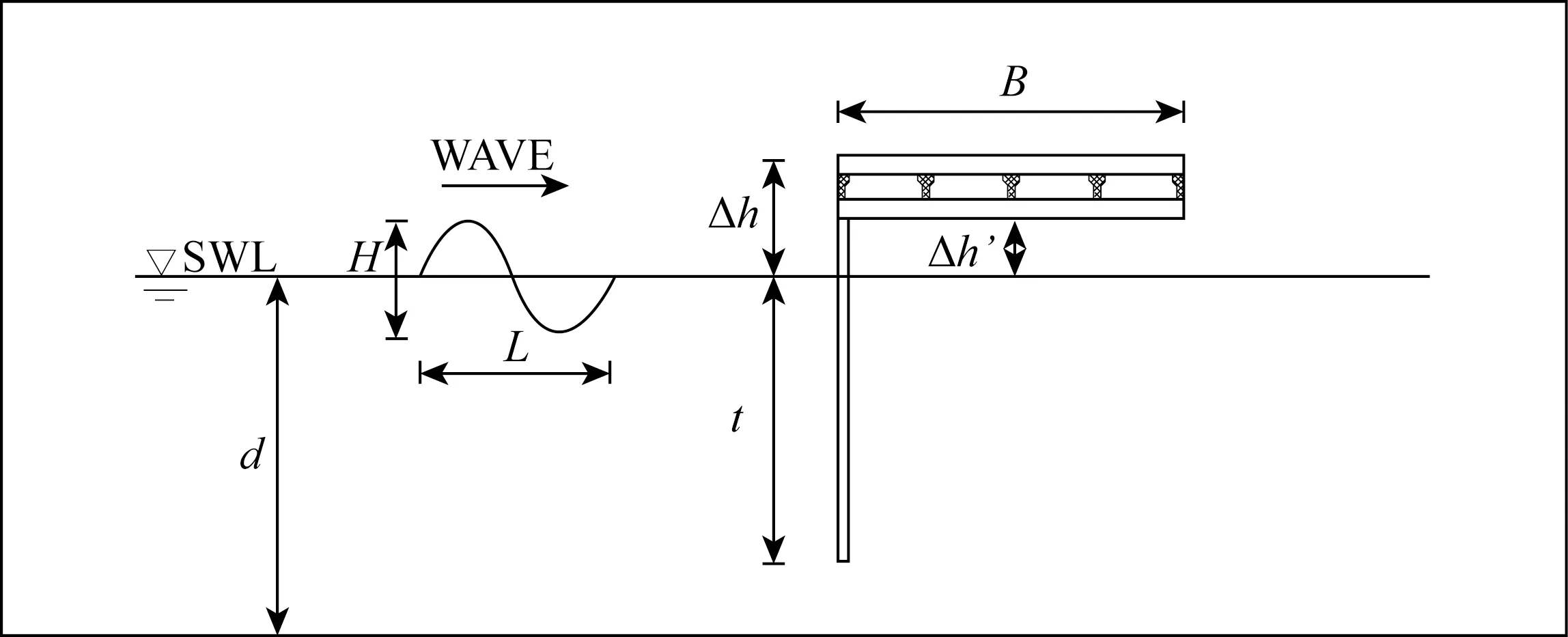
图2 垂直挡板式透空堤断面及各物理参数示意Fig.2 Sketch of the permeable breakwater section and definitions of the physical parameters

不规则波的期望谱选用JONSWAP谱，谱峰升高因子γ=3.3，波要素的率定均满足《波浪模型试验规程》(JTJ/T234-2001)[8]的相关要求。采用DJ800多功能采集系统进行波浪数据的采集，波浪的采集频率为50 Hz。编写Fortran程序，采用上跨零点法统计波高值，并通过调节阈值滤除毛疵，一个波列取不少于120个波进行统计，每组试验重复三次以确保测量数据的可靠性，并最终采用三次统计结果的平均值。

2 透浪系数的影响规律分析

波浪与垂直挡板式透空堤相互作用时，部分波浪能量被很快消耗掉，其中一部分波浪经挡板反射回去，反射波与入射波叠加，在堤前形成不完全立波；而另一部分波浪则从挡板底下穿透，或打击面板下部，或直接传至堤后，并与堤顶上部越浪后形成的波流水体相遇，一同在堤后形成新的波浪系列，该系列的稳定波高值即为透射波高。

透射波高的确定是研究透浪系数的一个关键，因此需首先分析堤后新波浪系列的沿程波高变化规律。图3为部分组次下堤后各测点波高的沿程变化情况，图中的横坐标为堤后各波高测点至堤轴线的水平距离，纵坐标为各测点对应的Hs。图中可见，堤后各测点Hs的沿程变化并不大，但由于水面壅高、波浪形态紊乱等原因使得堤后x=1 m、2 m测点处的波高较不稳定，统一将堤后相对较为稳定的x=3 m、4 m、5 m、6 m测点处的Hs取平均，该平均值即为透射波高Ht。

图3 堤后Hs的沿程变化Fig.3 Variations of Hs along the back of the breakwater

透浪系数Kt=Ht/Hi，其中Hi、Ht均取对应系列的有效波高值Hs。以下从入射波高、波周期、挡板相对入水深度、相对堤宽、挡板相对超高、面板相对超高等因素出发，分析其对透浪系数的影响规律。

2.1入射波高的影响

图4为h=0.095 m分别组合t=0.2 m和t=0.3 m的各组次下Kt随入射波高Hs变化而变化的情况。

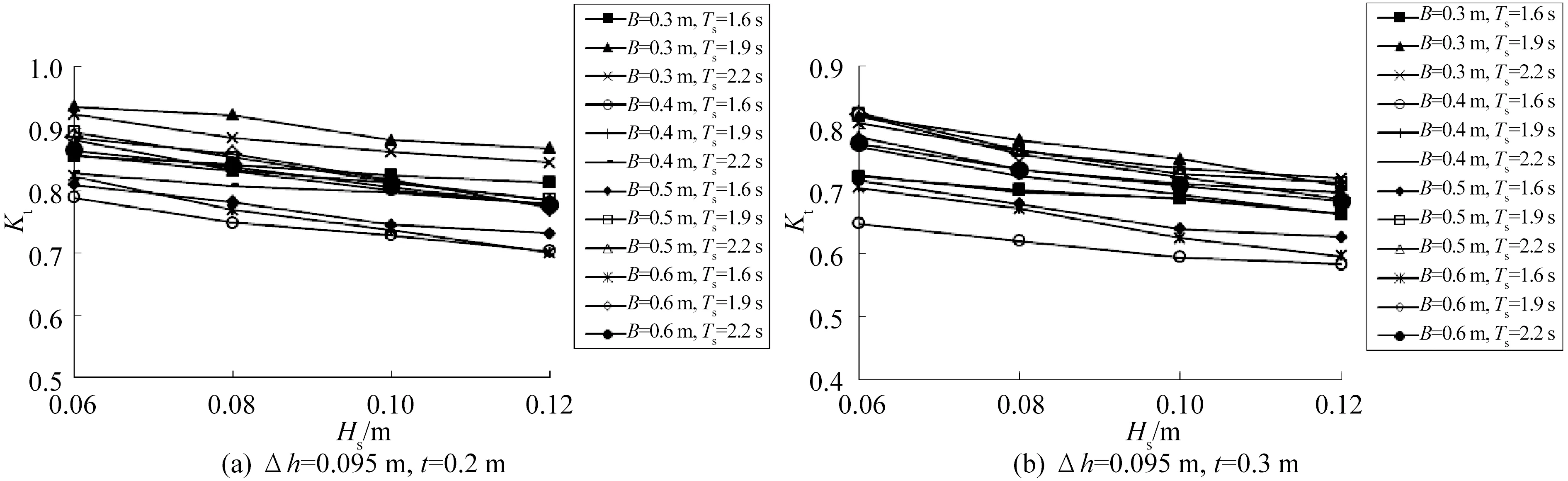
图4 Kt与Hs的关系Fig.4 Variations of Kt with the significant incident wave height Hs

图中可见，随着入射波高的增大，各组次下Kt均呈现减小的趋势，但减小的幅度并不大，其原因有二：一是入射波高的增大会直接导致挡板上部越浪量的增大，越浪水体将携带更多的动能传至堤后；其二是入射波高的增大使得挡板下部透射波浪打击面板底部的几率有所增大，水体紊动消能的效果更为明显，传至堤后的波能相对入射波的比例将大幅减小。综合这两个因素，入射波高的变化对于垂直挡板式透空堤的堤身上部越浪和下部透浪均会产生一定的影响，但对Kt的影响并不显著。

2.2波周期的影响

图5为△h=0.095 m分别组合t=0.2 m和t=0.3 m的各组次下Kt随波周期Ts变化而变化的情况。图中可见，Ts从1.3 s增大到1.9 s过程中，Kt随之明显增大，Ts从1.9 s增大到2.2 s过程中波周期的增大对Kt影响甚微。综上分析，在一定范围内，波周期越小，经透空堤结构后波浪水质点的紊动更为剧烈，消浪效果则越发突出。由此可见，波周期对Kt的影响较为显著。

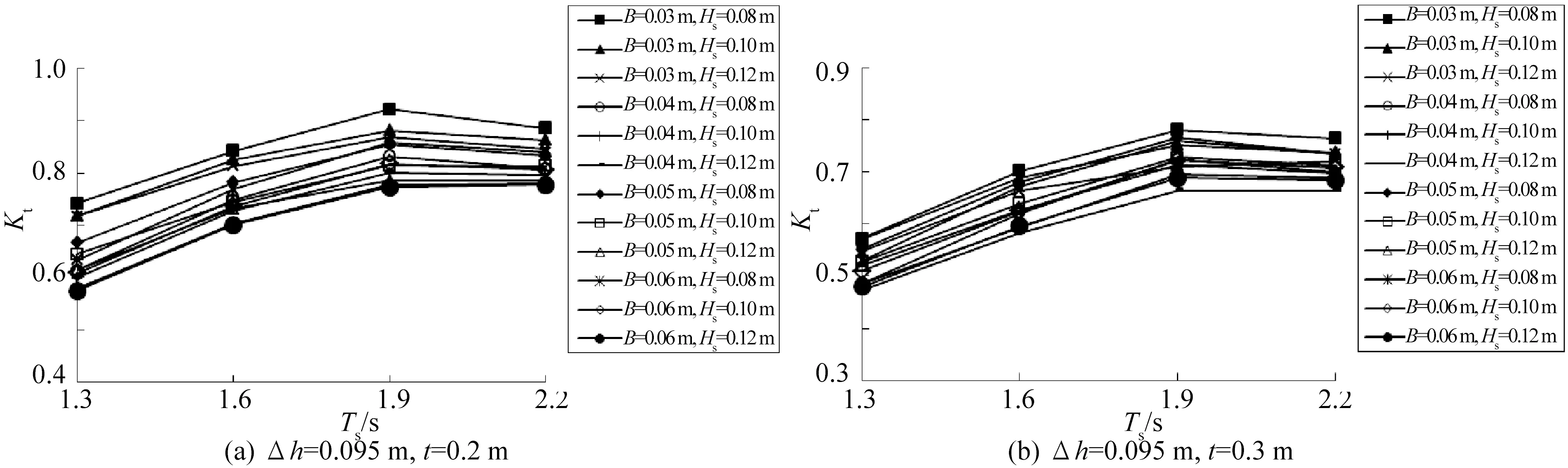
图5 Kt与Ts的关系Fig.5 Variations of Kt with the significant wave period Ts

2.3挡板相对入水深度的影响

引入挡板相对入水深度因子t/d，图6为Hs=0.10 m和Ts=1.6 s的各组次下Kt随t/d变化而变化的情况。图中可见，Kt随着t/d的增大而明显减小，且各组次的变化趋势较为一致。这是由于波浪能量大部分都集中在水体表层2～3倍波高的水深范围内，随着t/d的增大(0.2～0.8)，挡浪面积相应线性增大，水质点经垂直挡板碰撞后运动方向的改变越发明显，波能消耗更为剧烈，从而Kt随之明显减小。由此可见，挡板相对入水深度对Kt的影响十分显著。

图6 Kt与t/d的关系Fig.6 Variations of Kt with the relative immersed depth of the baffle t/d

2.4相对堤宽的影响

引入挡板相对入水深度因子B/Ls，图7为Hs=0.10 m的各组次下Kt随B/Ls变化而变化的情况。图中可见，Kt基本上随着B/Ls的增大而减小，其中当B/Ls=0.10～0.17时Kt的减小幅度相对较大，当B/Ls=0.22～0.26时Kt的减小趋势较为平缓。说明堤身的加宽将使传向堤后的一部分波浪能量进一步损耗，但相对堤宽到增大到一定程度后对透浪系数的影响将不再明显。

图7 Hs=0.10 m下Kt与B/Ls的关系Fig.7 Variations of Kt with the relative width of the breakwater B/Ls when Hs=0.10 m

2.5结构相对超高的影响

由于试验假定了挡板与面板顶部齐平且面板厚度0.02 m保持不变，挡板超高△h增大的同时面板超高△h′也相应增大(△h=△h′+0.02 m)，因此可将△h与△h′作为一个整体反映结构超高对透浪系数的影响。与挡板相对入水深度t/d相对应，引入△h/d作为挡板相对超高因子。考虑到面板底部的消浪程度与挡板底部透射波的波面高度关系密切，因此引入△h′/Hs作为面板相对超高因子。

在一定的入射波要素条件下，结构超高的增大会直接导致挡板上部越浪量的减小，从而堤后水面波动的振幅降低，意味着由结构上部传至堤后的透射波能量将随着结构超高的增大而减少；同时,从挡板下部穿透的波浪打击透空堤面板的几率也会减小，面板底部水体紊动消能的效果减弱，意味着由结构下部传至堤后的透射波能量将随着结构超高的增大而增多。

图8为B=0.4 m分别组合Hs=0.10 m和Ts=1.6 s的各组次下Kt随△h/d变化而变化的情况；图9为B=0.4 m的各组次下Kt随△h′/Hs变化而变化的情况。图中可见，Kt随△h/d、△h′/Hs的增大而小幅增大，说明挡板超高增大引起的Kt减小程度不及面板超高增大引起的Kt增大程度。值得注意的是，挡板相对超高△h/d与面板相对超高△h′/Hs都对Kt有一定的影响，两者的影响趋势是一个此消彼长的过程。

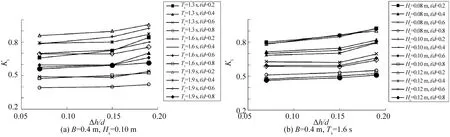
图8 Kt与△h/d的关系Fig.8 Variations of Kt with the relative superelevation of the baffle △h/d

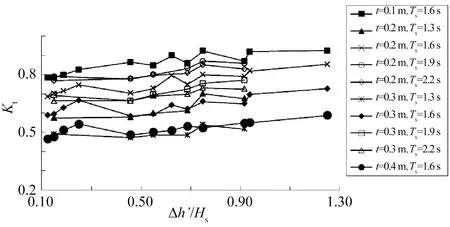
图9 B=0.4 m下Kt与△h′/Hs的关系Fig.9 Variations of Kt with the relative superelevation of the deck △h′/Hswhen B=0.4 m

3 透浪系数的计算方法

3.1与前人公式的比较

图10、图11分别为Kt的试验值与Wiegel理论公式、Kribel理论公式Kt计算值比较的结果。图中可见，Wiegel公式的计算值与试验值的误差相对较小，试验值普遍大于计算值约20%左右；Kribel公式的计算值与试验值的误差相对较大，试验值普遍比计算值大20%以上。但两理论公式都是仅考虑了挡板相对入水深度t/d和相对水深d/Ls这两个影响因素。

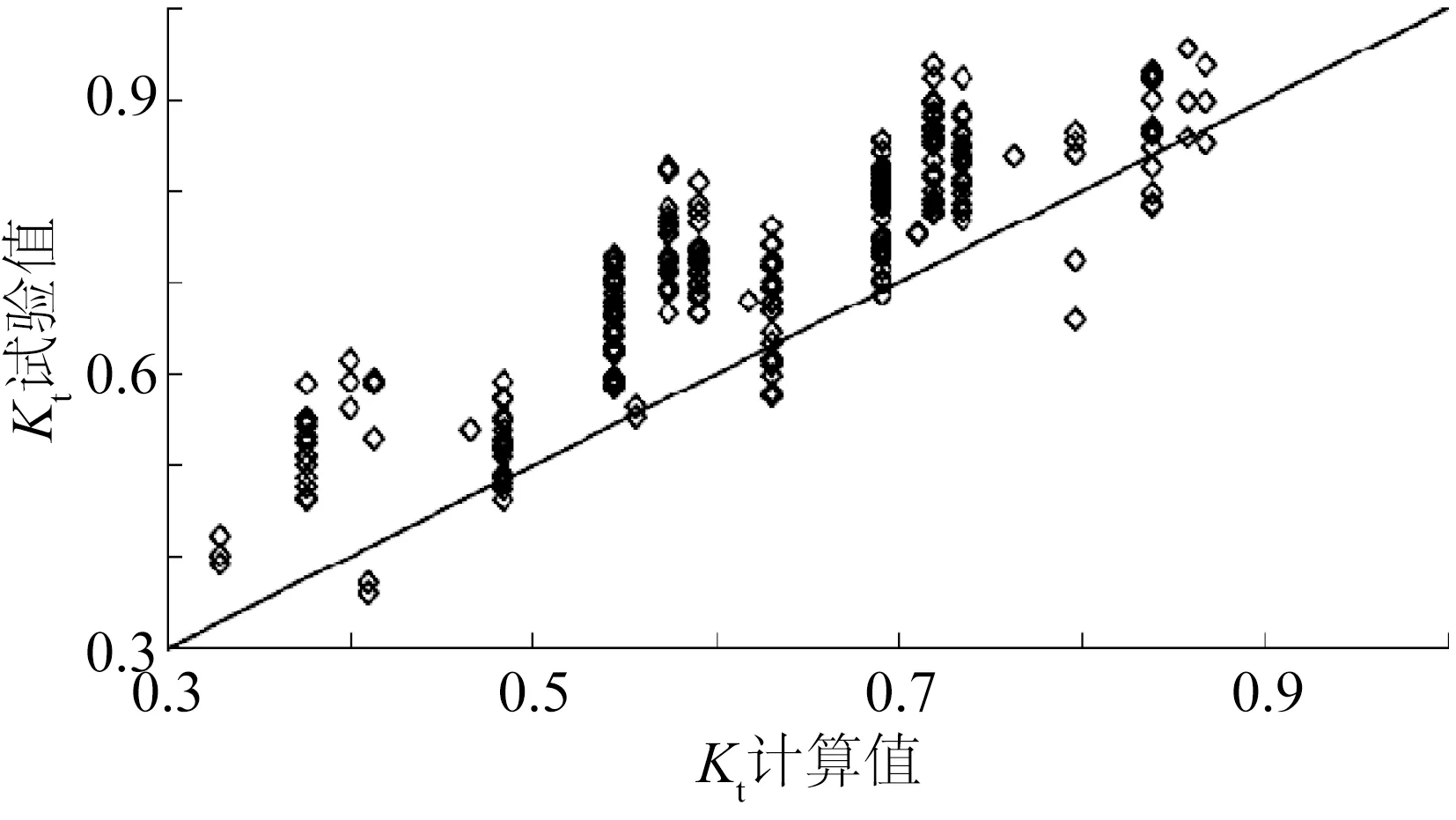
图10 Kt的试验值与Wiegel理论公式计算值比较Fig.10 Comparsions of the experimental values of Kt with the calculated values of Kt by the theoretical formula of Wiegel

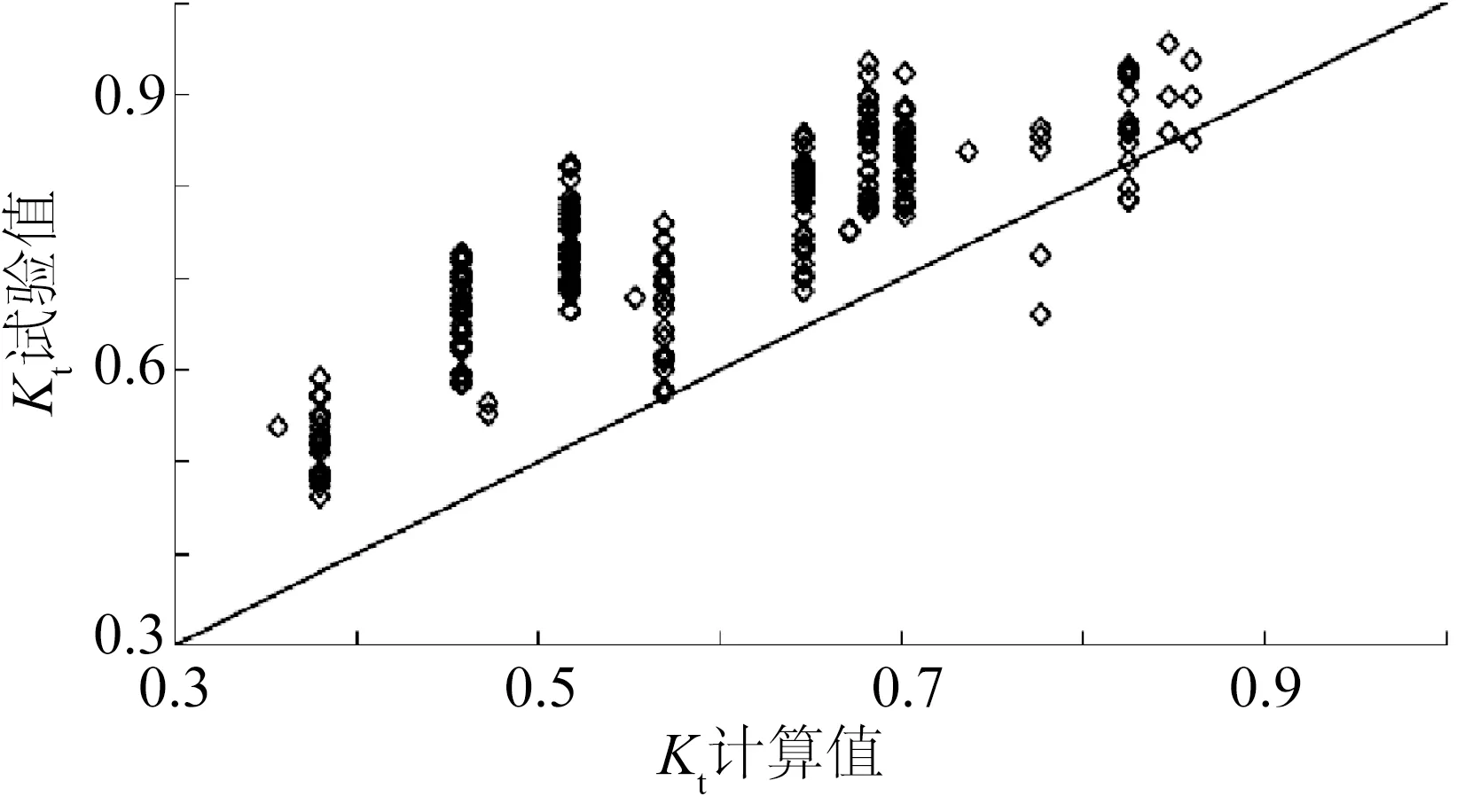
图11 Kt的试验值与Kribel理论公式计算值比较Fig.11 Comparsions of the experimental values of Kt with the calculated values of Kt by the theoretical formula of Kribel

图12 Kt的试验值与规范公式计算值比较Fig.12 Comparsions of the experimental values of Kt with the calculated values of Kt by the Code

图12为透浪系数Kt的试验值与规范公式计算值的比较情况。图中可见，规范公式的计算值与试验值的误差相对较大，其中大部分试验值比计算值偏大20%以上。规范公式的适用条件是双挡板的透空式防波堤结构，适用范围是B<0.5L，虽然适用范围较广，但堤宽、结构超高等因素均未考虑。

3.2计算公式的拟合

根据透浪系数的影响规律分析可知，挡板相对入水深度t/d、波周期Ts、挡板相对超高△h/d、面板相对超高△h′/Hs对透浪系数影响较大，为主要影响因素；相对堤宽B/Ls、入射波高Hs对透浪系数影响相对较小，为次要影响因素。考虑到试验水深d=0.5 m保持不变，根据微幅波理论，相同水深下波周期Ts的变化对应于波长Ls的变化，在此采用相对水深d/Ls来反映波周期Ts对透浪系数的影响。此外，考虑到入射波高Hs对透浪系数的影响有限且面板相对超高△h′/Hs已含波高因子，在此不再单独考虑Hs对透浪系数的影响。于是，采用因次分析的方法可得到以下关系式：

与前人计算公式的比较可知，Wiegel理论公式的Kt计算值与试验值吻合最好，但该公式未考虑挡板上部越浪和堤面板消浪对透浪系数的影响,在此挡板相对超高、面板相对超高及相对堤宽等因素也需得以反映。根据透浪系数与单个物理因子的变化趋势分析，在Wiegel理论公式的基础上，可假定垂直挡板式透空堤的透浪系数公式结构为：

其中，Wiegel理论公式

采用最小二乘法，对试验数据进行非线性拟合,得到式(2)的各经验系数如下：

k1=0.976，k2=0.089，k3=0.185，k4=0.732，k5=0.544，k6=0.896。

最终，得到透浪系数的计算公式如下：

此公式的适用范围如下：

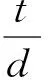
式中：d为水深；t为挡板入水深度；k为波数，k=2π/Ls；B为堤宽；Δh为挡板超高，即挡板顶部到静水面的高度；Δh′为面板超高，即面板底部到静水面的高度。

图13为本公式的Kt计算值与试验值比较的情况，公式的相关系数为0.958，均方差为0.036 42，公式适用范围较广，拟合精度较高。此外，本公式充分考虑了挡板超高、面板超高、相对堤宽对透浪系数的影响，实用性更强。

为进一步校验本公式的可靠性，收集了上海化学工业区孚宝透空式码头工程、海安新港荔枝湾码头透空式防波堤工程、上海吴淞口炮台湾船舶基地透空式防波堤工程三处实际工程的透浪系数Kt试验值，将相应的各物理参数代入本文公式计算Kt，比较后发现该计算值与各工程的Kt试验值差异并不大(见图14)，再次印证了本文公式的合理性。考虑到本文公式结构简单、影响因子全面，可供今后垂直挡板式透空堤的透浪系数估算。

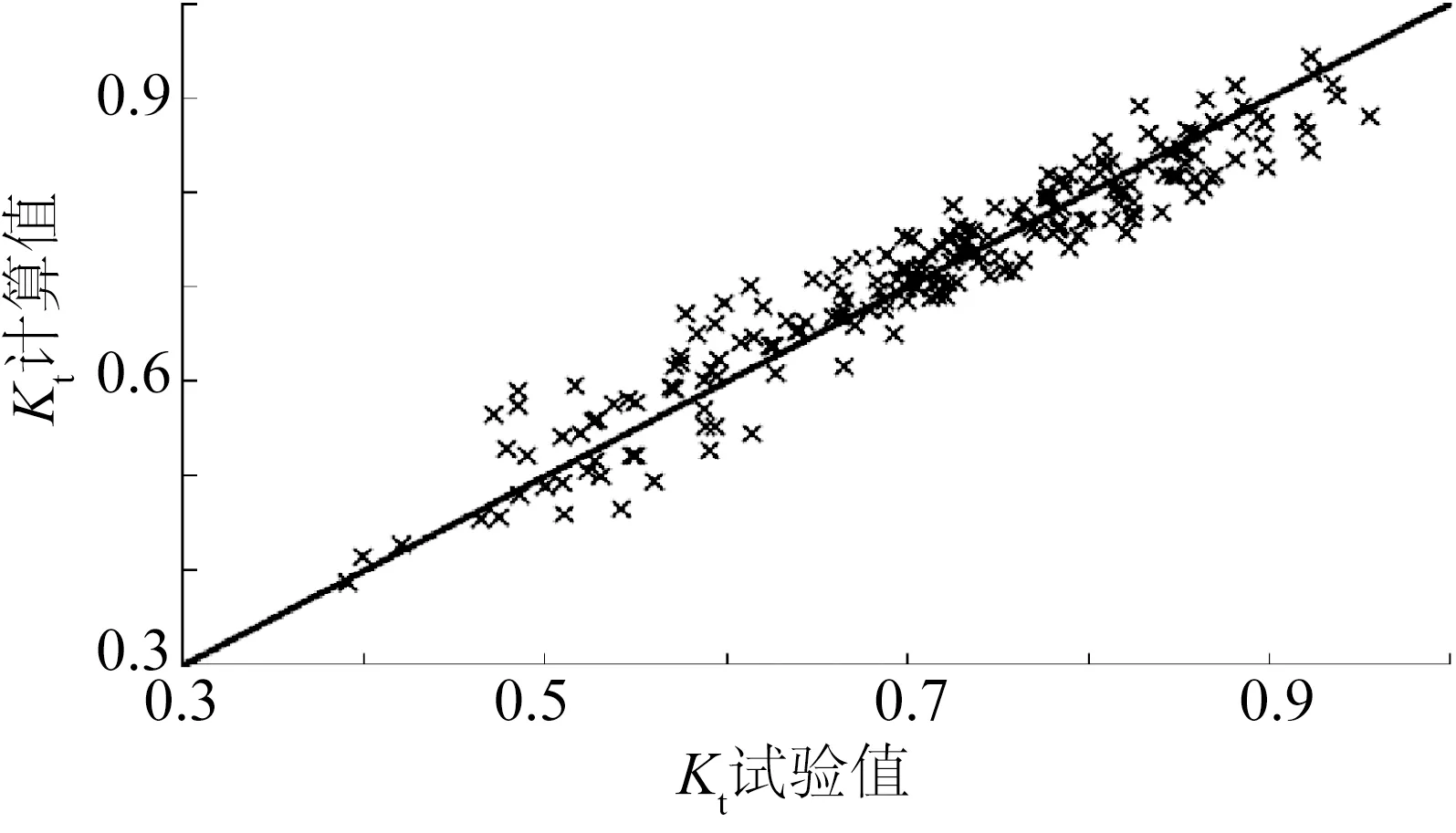
图13 本文公式的Kt计算值与试验值比较Fig.13 Comparisons of the calculated values of Kt by present formula with the experimental values of Kt

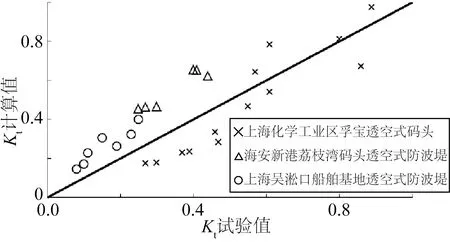
图14 三处实际工程采用本文公式的Kt计算值与试验值比较Fig.14 Comparisons of the calculated values of Kt by present formula of three practical projects with its experimental values of Kt

4 结 语

通过模型试验，对不规则波作用下垂直挡板式透空堤的透浪系数进行了探讨，得到以下主要结论：

1)从入射波要素的角度分析，透浪系数Kt对入射波高Hs并不敏感，但会在一定范围内随波周期Ts的增大而显著增大。从透空堤结构的角度分析，透浪系数Kt随挡板相对入水深度t/d的增大而显著减小，并随相对堤宽B/Ls的增大而小幅减小；Kt随相对挡板超高Δh/d增大而减小的程度不及Kt随面板相对超高△h′/Hs增大而增大的程度，使得Kt总体上表现出随结构相对超高增大而小幅增大的趋势。

2)在Wiegel理论公式的基础上，对试验数据进行非线性拟合，得到了垂直挡板式透空堤透浪系数Kt的计算公式，公式充分考虑了挡板超高、面板超高和相对堤宽的影响，适用范围较广，拟合精度较高，经三处实际工程Kt试验值的校验结果良好。本文公式可作为今后类似透空式防波堤结构透浪系数的近似估算，具有一定的科学意义和工程意义。

3)考虑到垂直挡板式透空堤的结构型式仍可进一步细化，加之透空式防波堤的波能耗散原理至今未被完全掌握，下一步的研究重点应是更为深入的机理分析，并结合实际工程和模型试验辅以验证比较。

[1] URSELL F.The effect of a fixed vertical barrier on surface waves in deep water [C]// Proceedings of the Cam Bridge Philo Sophical Society.1947，43：374-382.

[2] WIEGEL R L.Transmission of wave past arigid vertical thin barrier [J].Journal of the Waterways and Harbors Division，1960，86(1) ：1-12.

[3] KRIEBEL D L,BELLMANN C A.Wave transmission past vertical wave barriers [C]//Proceedings of the 25th Coastal Eng.Conf..1996.

[4] JTJ298-98，防波堤设计与施工规范[S].北京：人民交通出版社，1998：1-23.(JTJ298-98，Code of design and construction of breakwaters [S].Beijing：China Communications Press，1998：1-23.(in Chinese))

[5] 麻志雄．透空式防波堤消浪性能试验研究[R].南京：南京水利科学研究院，2002：1-6.(MA Zhixiong.Experimental study on the wave dissipation of permeable breakwater [R].Nanjing：Nanjing Hydraulic Research Institute，2002：1-6.(in Chinese))

[6] 严以新，郑金海，曾小川，等．多层挡板桩基透空式防波堤消浪特性试验研究[J].海洋工程，1998，16(1) ：67-74.(YAN Yixin，ZHENG Jinhai，ZENG Xiaochuan，et al.Characteristics of wave dissipation for pile-foundation tier-retainer breakwaters [J].The Ocean Engineering，1998，16(1) ：67-74.(in Chinese))

[7] 钟瑚穗，徐昶，过达．桩基透空堤的透浪系数[J].中国港湾建设，2003，10 (5) ：21-24.(ZHONG Husui，XU Chang，GUO Da.Wave transmission factors of permeable breakwater on pile foundation [J].China Harbour Engineering，2003，10 (5) ：21-24.(in Chinese))

[8] JTJ/T234-2001，波浪模型试验规程[S].北京：人民交通出版社，2002：8-15.(JTJ/T234-2001，Wave model test regulation [S].Beijing：China Communications Press，2002：8-15.(in Chinese))

An experimental study of the wave-permeating coefficient of vertical baffle permeable breakwater under irregular waves

SHAO Jie1，CHEN Guoping2，YAN Shichang2，YANG Qin3

(1.Zhejiang Institute of Hydraulics & Estuary,Key Laboratory of Estuary and Coast of Zhejiang Province,Hangzhou 310020,China; 2.Key Laboratory of Coastal Disaster and Defence,Ministry of Education,Hohai University,Nanjing 210098,China; 3.Jiangsu Province Communications Planning and Design Institute Limited Company,Nanjing 210014,China)

TV139.2;U656.2

A

10.16483/j.issn.1005-9865.2016.01.007

1005-9865(2016)01-0050-08

2015-04-13

浙江省自然科学基金(LQ16E090004)；浙江省科技计划项目(2016F50019)

邵 杰(1984-)，男，浙江宁波人，工程师，硕士，主要从事海岸及海洋工程研究。E-mail：hldss008@163.com