水深对软刚臂单点系泊FPSO动力响应的影响

刘成义，唐友刚，李 焱

(1.天津大学 建筑工程学院，天津 300072；2.天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

水深对软刚臂单点系泊FPSO动力响应的影响

刘成义1,2，唐友刚1,2，李 焱1,2

(1.天津大学 建筑工程学院，天津 300072；2.天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

系泊系统的定位能力是浅水油田作业的软刚臂式单点系泊FPSO安全作业的重要保障,为研究不同水深/吃水比下单点系泊系统的受力性能，针对一艘16万吨级软刚臂单点系泊FPSO，在线性三维势流理论的基础上，基于多体动力学方法，建立FPSO-系泊腿-软刚臂的耦合模型，采用Newman近似法和Pinkster近似法分析了FPSO所受二阶波浪力，在时域内计算了不同水深/吃水比对系泊系统动力响应性能的影响。结果表明，随着水深/吃水比的增加，Newman近似法计算得到二阶波浪力先增大后减小，引起单点系泊系统载荷先增大后减小；而Pinkster近似法计算得到的二阶波浪力逐渐减下，引起单点载荷逐渐减下。在浅水条件下，Pinkster近似法具有较好的适用性，Newman近似法严重低估了FPSO所受的二阶波浪力；在深水条件下，Newman近似法能满足工程计算的要求；适用两种方法的临界水深/吃水比为1.64。

多体动力学；软刚臂系泊系统；Newman/Pinkster近似法；二阶波浪力；动力响应性能；水深/吃水比

Abstract:With the increasing operation life of FPSO and mooring systems,there have been some accidents,which have a great impact on safety in production in oil field.More attentions have been paid to the safety of the Soft Yoke Mooring Systems(SYMS).Dynamic response capability of the SYMS under different WD/T(Ratio of Water depth and FPSO Draft) was analyzed based on multi-body dynamic method.The multi-body coupling model including SYMS and FPSO was established and the hydrodynamic parameter of each body was calculated with linear 3-D potential theory.Second-order wave drift force was calculated by Newman approximation and Pinkster approximation,and the forces on the SYMS under different WD/T were analyzed afterward.A comparison of results using different approximation methods was carried out.With the Newman approximation,the second-order wave force increases first and decrease afterwards with the increase of WD/T,leading to the forces on the SYMS changing synchronously; with the Pinkster approximation,the second-order wave force continually decreases with the increase of WD/T,leading to the forces on the SYMS changing synchronously.It is concluded that Pinkster approximation has a good applicability in shallow water while Newman approximation can meet the requirements of engineering calculations in deep water; and the threshold of WD/T is 1.64.

Keywords:multi-body method; soft yoke mooring system; Newman/Pinkster approximation; second-order wave drift force; dynamic response; ratio of water depth and draft

对于浅水油田作业的软刚臂式单点系泊FPSO，其系泊系统的定位能力是FPSO安全作业的重要保障。在浅水条件下，水深变化将会极大地影响FPSO所受的二阶波浪力，进而对系泊系统的载荷产生影响。

FPSO所受二阶波浪力主要包括平均漂移力、二阶慢漂波浪力及二阶和频波浪力，国内外学者已经对FPSO所受二阶波浪力受水深的影响做了大量地研究。

在二阶波浪力的计算方法上，Guilaume等[1]对二阶低频载荷的计算方法进行总结，指出目前计算二阶波浪载荷传递函数(QTF)矩阵的主要方法有：全QTF法、忽略自由表面积分的全QTF法、Pinkster近似法以及Newman近似法四种。QTF矩阵主对角线元素为平均漂移力的传递函数，主要计算方法为近场法、远场法两种；非主对角线元素为二阶差频波浪载荷传递函数，完整的数值计算将耗费大量的时间及计算资源，通常通过Newman近似或Pinkster近似法求解。也有学者对以上计算方法进行了改进，Chen等[2]将远场法与近场的压力积分法相结合，提出了计算平均漂移力的中场法；Cong等[3]基于高阶边界元和自适应的单元积分法，提出了一种新的低频慢漂力的计算方法；但这些改进算法应用并不广泛。目前，二阶波浪力的计算仍然以Newman近似法和Pinkster近似法为主。

关于水深变化对FPSO所受二阶波浪力的影响，陈忆宁等[4]在不考虑系泊系统的情况下，以一艘16万吨级的FPSO为对象，分别采用Newman近似法和全QTF方法计算不同水深下FPSO所受的二阶波浪力，结果表明，Newman近似法在深水条件下具有较好的适用性。Naciri等[5]采用有限元方法对浅水 LNG 船水动力特性进行分析，并与实验结果进行对比，认为对于浅水中船形海洋结构物所受二阶波浪力，Pinkster 近似法可以满足计算和研究的要求。李欣等[6]分别采用Pinkster近似法和实验的方法，研究浅水条件下不同水深对FPSO所受二阶波浪力的影响，结论认为二阶波浪力/力矩随水深的增大而减小。Fonseca和Pessoa等[7-8]用数值和实验方法研究了双色波作用下固定浮体上所受的一阶波浪力、平均漂移力以及二阶差频波浪力随水深变化的规律，认为随水深的减小，波浪二阶力明显增大，一阶力略有增大，且浅水中二阶波浪力的计算较之于深水中更为重要。Xiao等[9]以软刚臂单点系泊方式定位于浅水油田的16万吨级FPSO为对象，通过实验研究不同水深下的低频纵荡运动和系泊力，结论认为：低频纵荡运动和系泊力随着水深的减小大大增加，在水深吃水比较小时，力的增加非常剧烈。

可见，目前大部分研究将FPSO视作固定的海洋结构物，研究水深变化对其所受二阶波浪力的影响，并未考虑FPSO在实际系泊状态下的动态效应；亦未考虑水深变化对软刚臂单点系泊系统的动力响应性能的影响。为研究水深变化对软刚臂式单点系泊FPSO系泊系统动力响应性能的影响，本文基于多体动力学的方法，分别采用Newman近似法和Pinkster近似法考虑二阶波浪载荷，在时域内计算了不同水深/吃水比(WD/T)下单点系泊系统载荷，得到系泊系统载荷随WD/T的变化规律，并对比两种方法的计算结果，分析产生这种差别的原因；考虑到Newman近似法在深水条件下具有很好的适用性，而Pinkster近似法对浅水条件下的二阶波浪载荷具有更高的模拟精度，并进一步给出了适合用Pinkster近似法计算和Newman近似法计算的临界WD/T值，为工程实际提供参考。

1 多体耦合计算模型

1.1FPSO及系泊系统主尺度参数

FPSO所在海域水深为17.83 m，其主要参数如表1所示。软刚臂系泊系统(soft yoke mooring system，SYMS)由软刚臂及两侧系泊腿组成，主尺度参数以及软刚臂结构坐标系、系泊腿结构坐标系如图1所示，其中软刚臂与压载舱总重量为1 850 t，单个系泊腿重量为75 t。

1.2全耦合有限元模型的建立

对于软刚臂单点系泊系统，传统的计算方法通常将单点简化为约束纵荡运动的非线性刚度弹簧，研究FPSO的运动响应或者单点的受力，这种方法很难模拟系泊机构的实际运动特性。对此，许多学者基于多体动力学方法，对软刚臂式单点系泊FPSO进行了实验和数值研究。Wang[10]等以浅水软刚臂系泊的FPSO为研究对象，采用多体方法模拟水下软刚臂系泊实际结构和FPSO的耦合作用，对FPSO的运动和动力响应进行研究；Guo等[11]通过时域内的数值模拟和模型试验，研究了非线性海洋环境下浅水FPSO运动响应特性，并进行甲板上浪分析；Phadke等[12]基于多体方法，对软刚臂单点系泊的“蓬勃号”FPSO系泊系统的安装进行数值分析，得到较为合理的结果。这些研究很好地证明了多体方法的适用性，文中对FPSO系泊系统的建模，也是基于多体方法进行的。

采用ANSYS建立全船及系泊刚架的有限元模型，导入AQWA中进行水动力及时域响应计算。考虑到船艏尾的形状较为复杂，定义船艏尾的网格密度为2 m，船中的网格密度为3 m。

FPSO及系泊刚架的有限元模型如图2所示，模型的单元总数为8 063。多体耦合模型中包含四部分结构：FPSO及船艏系泊刚架通过刚性连接组成第一部分结构；两侧系泊腿为两个结构，上端与船艏系泊刚架通过双轴铰连接，释放横摇、纵摇两个自由度的约束；下端与软刚臂通过三轴铰连接，释放3个转动自由度的约束；包含压载舱的软刚臂为第四部分结构，软刚臂与塔架系泊点处释放3个转动自由度的约束。

表1 FPSO主要参数Tab.1 Main particulars of FPSO vessel

图1 软刚臂及系泊腿的主要尺度Fig.1 Main dimensions of the yoke and pendent

图2 软刚臂单点系泊FPSO全耦合有限元模型Fig.2 Completely-coupled model of the FPSO and SYMS

2 计算理论

2.1多体耦合时域运动方程

综合考虑波浪、风、流载荷以及单点系泊系统的回复力的联合作用，软钢臂式单点系泊FPSO在时域内的运动方程为[13]：

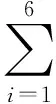
其中，M为FPSO质量矩阵，通过FPSO质量以及各回转半径求得；A()为最大计算频率对应的附连水质量矩阵，r(t)为辐射阻尼的脉冲响应函数矩阵，附连水质量、辐射阻尼系数均采用三维势流理论应用源汇分布法计算得到；D为FPSO慢漂阻尼矩阵，对于文中软刚臂式单点系泊FPSO，纵荡、横荡和艏摇自由度低频漂移阻尼参照BV规范中的公式进行计算；K为FPSO静水回复力刚度矩阵，根据FPSO水动力性能求得；F(1,2)(t)为一阶、二阶波浪载荷；Fw(t)为风载荷，Fc(t)为流载荷，风、流载荷参照OCIMF规范进行计算；FSPM(t)为单点系泊系统提供的回复力。

A字型刚臂结构是在系泊单点、两侧系泊腿拉力下保持平衡，其受力形式较为简单，此处不列出结构动力方程。

两侧系泊腿作为FPSO与A字型刚臂的连接杆，其时域运动方程：

式中：mp为系泊腿质量矩阵，Kp为考虑结构之间相互影响的12×12的全耦合刚度矩阵。

2.2波浪载荷计算

选用JONSWAP谱模拟不规则海浪，根据谱峰因子取为1.8。基于选定的波浪谱，通过傅里叶变换可以得到时域内的随机波面升高，进而可通过卷积积分的方式生成一阶、二阶波浪载荷的时域历程。在不规则波浪作用下，作用在结构物上的瞬时波浪力可以写为：

基于Newman近似法可得：

基于Pinkster近似法可得：

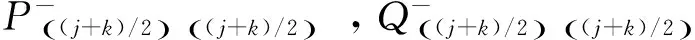
2.3动力响应计算结果

动力响应计算方法：在多体系泊分析模块AQWA-DRIFT中，基于多刚体动力学方法，根据FPSO、软刚臂以及系泊腿的时域运动方程，分别建立两侧系泊腿及软刚臂的振动方程，在时域内通过连接点处的载荷传递实现耦合，建立多体的时域耦合方程，进行迭代计算。由于计算中计入了系统内包括慢漂阻尼、非线性风流载荷等在内的非线性项，采用数值解法求解非线性多体耦合振动方程组，因此，该方法可模拟实际环境工况下FPSO的运动响应及单点系统的受力。

系泊系统的动力响应计算所选取两种典型的海洋环境工况如表2所示，分别考虑了风、浪、流同向与不同向两种工况，计算水深为17.8 m。

根据表2给出的工况，采用多体动力学方法进行FPSO及单点系泊系统的耦合动力分析，模拟软刚臂单点系泊机构的具体连接形式，考虑软刚臂及系泊腿加速度惯性力项对FPSO运动响应及单点系统载荷的影响，分别采用Newman近似法和Pinkster近似法模拟FPSO所受的二阶波浪力，计算塔架系泊点处软刚臂结构坐标系下三个方向的载荷Fx、Fy、Fz以及系泊腿的轴向载荷Pt，在时域内统计各载荷的最大值，结果如表3所示。

根据动力响应计算结果看出，在工况1中，风、浪、流同向，由于系泊系统具有风标效应，单点y方向载荷较小，接近于0，可以忽略不计， Pinkster近似法的计算结果略大于Newman近似法的计算结果；原因在于FPSO迎浪条件下受力面积较小，低频二阶力作用不明显。在工况2中，风、浪、流不同向，FPSO与波浪有夹角，单点各方向载荷皆不为0，且Pinkster近似法的计算结果远大于Newman近似法的计算结果；原因在于，FPSO此时与波浪方向有一定的夹角，二阶力作用范围大，浅水波浪力的二阶非线性效应明显，Newman近似法严重低估了波浪二阶力的作用，造成其计算结果远小于Pinkster近似法的计算结果。

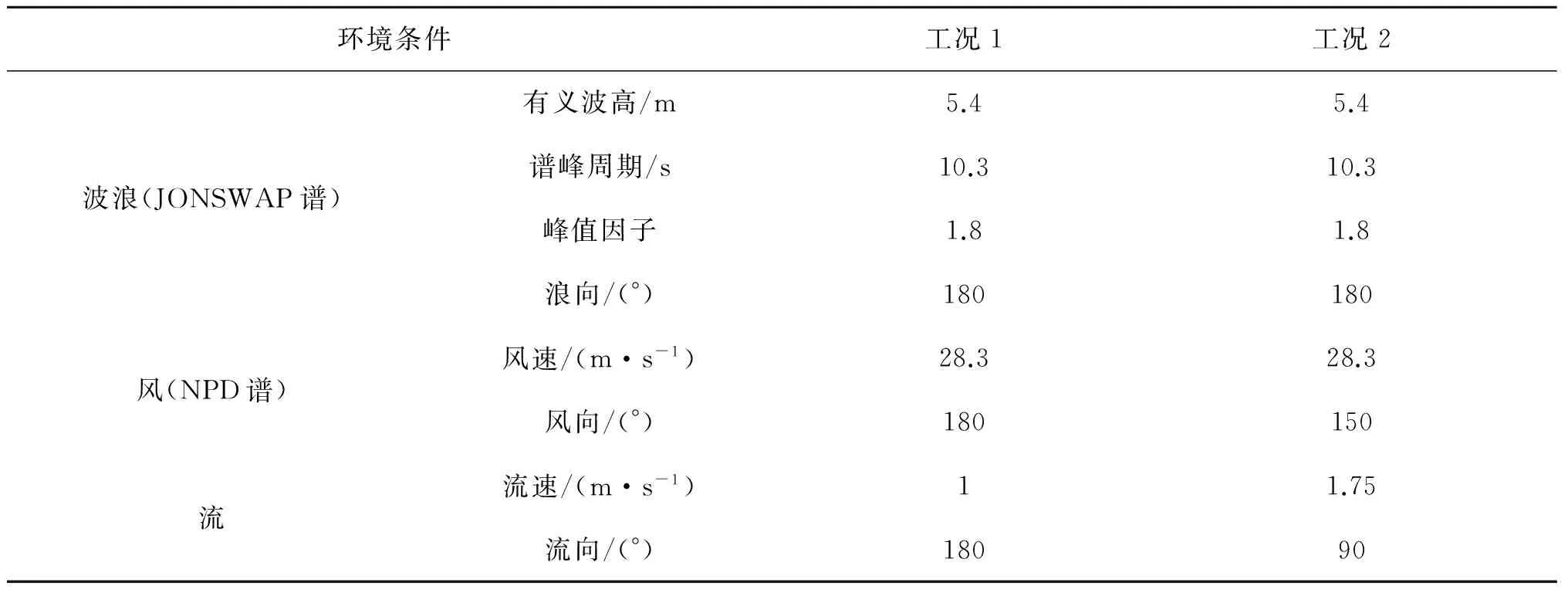
表2 海洋环境条件Tab.2 Environment conditions

表3 塔架系泊点载荷及系泊腿轴力最大值Tab.3 Maximum dynamic response of the SYMS

注：单点载荷(Fx、Fy、Fz)皆为软刚臂结构坐标系下载荷结果。

3 不同WD/T动力响应分析

在水深的敏感性分析中，FPSO吃水(T)为14.5 m，以该海域实际水深(WD)17.8 m为基准，每次增加3 m，选取五个水深作为浅水海况，并额外选取了50 m、75 m、100 m三个水深作为深水海况，所选取的水深为17.8、20.8、23.8、26.8、29.8、50、75、100 m，对应的WD/T依次为1.23、1.43、1.64、1.85、 2.06、3.45、5.17、6.90。分别采用Newman近似法和Pinkster近似法计算软刚臂单点系泊系统载荷，分析系泊系统载荷随WD/T变化的规律，并对比两种方法的计算结果。

此外，由于Newman近似法与Pinkster近似法的根本差别在于二阶波浪力的计算方法不同，为分析单点系泊系统载荷随WD/T的变化规律产生的原因，文中对两种近似方法下FPSO所受二阶波浪力随WD/T的变化规律进行了对比分析。

3.1工况1系泊系统受力结果

对于风、流、浪同向的工况1，软刚臂单点系泊系统具有风标效应，FPSO仅受到纵荡方向的载荷，单点系泊系统受力主要包括单点载荷Fx、Fz和系泊腿轴向载荷Pt。根据2.3节动力响应分析方法，进行不同WD/T条件下时域计算，统计单点系泊系统载荷最大值，计算结果如图3所示。

根据计算结果，在风、浪、流同向条件下，可得出如下结论：

1)采用Newman近似法计算时，随WD/T的增加，单点x方向的载荷Fx先减小后增大，到深水区域后增大趋势平缓；单点z方向的载荷Fz和系泊腿轴力Pt均逐渐增加，但变化不大。

2)采用Pinkster近似法计算时，随着WD/T的增加，单点x、z方向载荷Fx、Fz和系泊腿轴力Pt呈现相同的规律，在浅水区域逐渐减小，深水区域趋于平缓；且Pt变化明显，Fx、Fz变化不大。

3)对比两种方法下系泊系统载荷的计算结果，可以看出：在浅水区域，采用Pinkster近似法计算得到的单点系泊系统载荷大于Newman近似法所得到的结果；深水区域，Pinkster近似法得到的结果反而小于Newman近似法；其临界水深吃水比为1.64，因此，认为在WD/T≥1.64时，Newman近似法可满足工程计算的要求。

图3 工况1系泊系统载荷随WD/T变化曲线Fig.3 Forces of SYMS vs.WD/T in Condition 1

图4 工况1中FPSO纵荡漂移力随WD/T变化曲线Fig.4 Wave drift forces of FPSO in surge direction vs.WD/T in Condition 1

3.2工况1漂移力计算结果分析

对于风、浪、流同向的工况1，图4给出两种方法下FPSO所受二阶波浪漂移力随WD/T增加而变化的规律。

随着WD/T增加，Newman近似法计算得到的FPSO漂移力先增大后减小，到深水区域又有微弱的增大趋势，与单点x方向的载荷呈现相互对应的规律；Pinkster近似法计算得到的FPSO漂移力先减小后逐渐趋于平稳，与单点系泊系统载荷的变化趋势呈现较好的对应规律；可见，单点系泊系统载荷Fx、Fz、Pt随WD/T增加而变化的情况直接受到FPSO所受的漂移力的影响。

3.3工况2系泊系统受力结果

对于风、浪、流不同向的工况2，在软刚臂结构坐标系下，单点系泊系统载荷包括Fx、Fy、Fz以及系泊腿轴向载荷Pt，统计不同 下各系泊系统载荷最大值，结果如图5所示。由结果可知：

1)采用Newman近似法计算时，随着WD/T增加，单点系泊系统各载荷括Fx、Fy、Fz都先增大后减小，在深水区域趋于平缓，在WD/T=2.06(水深29.8 m)处出现峰值。

2)采用Pinkster近似法计算，WD/T介于1.23～1.64(水深17.8～23.8 m)之间时，随WD/T增加，系泊系统各项载荷逐渐减小；WD/T介于1.64～2.05(水深23.8～29.8 m)之间时，随WD/T增加，系泊系统各项载荷逐渐增大；在WD/T大于2.06后(水深大于29.8 m)，随WD/T增加，系泊系统各项载荷逐渐减小，在深水区域趋于平缓。

图5 工况2系泊系统载荷最大值随WD/T变化曲线Fig.5 Forces of SYSM vs.WD/T in Condition 2

3)对比Pinkster近似法和Newman近似法下计算得到的单点载荷结果，可以看出：①在各个WD/T条件下，Pinkster近似法的计算结果均大于Newman近似法计算结果；②在极浅水区域，WD/T介于1.23～1.64之间时，随着WD/T的增加，Pinkster近似法计算时系泊系统各项载荷逐渐减小，而Newman近似法计算得到的各项载荷逐渐增加，二者呈现出相反的变化规律，且Pinkster近似法计算结果远大于Newman近似法的计算结果；③ 超过1.64(水深23.8 m)后，随着WD/T的增加，两种方法计算得到的系泊系统载荷都呈现先增大后减小变化规律，到深水区域后趋于平缓，都在WD/T(水深29.8 m)处出现峰值； Pinkster近似法计算得到的载荷略大于Newman近似法计算结果。

4)在WD/T≥1.64时，Newman近似法和Pinkster近似法计算的结果随水深的变化规律一致，且二者之间差别不大，可以认为Newman近似法满足工程实际的计算要求。

3.4工况2漂移力计算结果分析

对于风、浪、流不同向的工况2，图6给出不同方法下WD/T改变时FPSO在横荡、纵荡自由度所受漂移力，图7给出FPSO所受艏摇自由度漂移力矩。根据漂移力计算结果可知：

1)采用Newman近似法计算时，随WD/T的增加，FPSO所受的二阶波浪力变化规律为：在纵荡方向上，漂移力变化较小，从浅水区域到深水区域略有增大；横荡方向上，漂移力先减小后逐渐趋于平缓；艏摇方向上，漂移力先增大后减小，在深水区趋于平缓。对比系泊系统载荷与FPSO所受二阶波浪力随WD/T的变化规律可知，在Newman近似法条件下，系泊系统载荷与艏摇方向漂移力的变化规律一致。

2)采用Pinkster近似法计算FPSO二阶差频力时，随WD/T的增加，FPSO所受的漂移力变化规律为：在纵荡方向上，漂移力逐渐减小后趋于平缓，整体变化较小；横荡方向上，当WD/T≤2.06时，漂移力先减小后增大，随后漂移力逐渐减小并趋于平缓；艏摇方向上，漂移力先减小后趋于平缓，在浅水区域内，艏摇漂移力矩接近一阶艏摇波浪力矩。可见，在Pinkster近似法条件下，单点系泊系统载荷随WD/T增加而变化的规律与FPSO横荡、纵荡、艏摇方向度所受漂移力变化的规律都有很好的一致性。

3)对比两种近似法下漂移力计算结果，发现FPSO横荡方向漂移力差别不大，在浅水区域，Pinkster近似法载荷计算结果较大；在深水区域，Newman近似法的载荷计算结果较大。

综上所述，在风、浪、流不同向条件下，软刚臂单点系泊系统载荷的变化规律主要由FPSO艏摇方向所受的漂移力矩决定。

图6 工况2FPSO漂移力随WD/T变化曲线Fig.6 Wave drift forces of FPSO vs.WD/T in Condition 2

图7 工况2FPSO艏摇漂移力随WD/T变化曲线Fig.7 Wave drift forces of FPSO in yaw direction vs.WD/T in Condition 2

4 结 语

针对一艘浅水田油田作业、吃水为14.5 m的16万吨级软刚臂单点系泊FPSO，基于多体动力学方法，分别采用Newman近似法和Pinkster近似法计算了不同WD/T下FPSO所受的二阶波浪力和软刚臂单点系泊系统载荷，研究各载荷随WD/T的变化规律，得出以下结论：

1)采用Newman近似法计算时，随着WD/T的增加，FPSO所受的漂移力先增大后减小，引起单点系泊系统载荷的先增大后减小。

2)采用Pinkster近似法计算时，随着WD/T的增加，FPSO所受的漂移力逐渐减小，引起单点系泊系统载荷的逐渐减小。

3)在浅水区域，风、浪、流同向时，单点系泊系统载荷随WD/T的变化规律由FPSO所受到纵荡方向的二阶波浪力决定；风、浪、流不同向时，系泊系统载荷随WD/T变化的规律由艏摇方向的二阶波浪力矩决定。

4)浅水条件下，二阶波浪力非线性效应明显，采用Newman近似法计算仅能获得定常的低频漂移力成分，无法获得其高频与低频成分，因此该方法不能满足实际工程要求。

5)对于吃水为14.5 m的软钢臂单点系泊FPSO，在WD/T≤1.64时，浅水效应明显，采用Pinkster近似法较为准确的估算FPSO所受的二阶力更符合工程实际状况；在WD/T≥1.64时，Newman近似法可满足工程计算的要求；这两种方法计算二阶波浪力的临界WD/T为1.64。

[1] DE HAUTECLOCQUE G,REZENDE F,WAALS O,et al.Review of approximations to evaluate second-order low-frequency load[C]//Proceedings of the 31st International Conference on Ocean,Offshore and Arctic Engineering.2012:363-371.

[2] CHEN X B,REZENDE F.Efficient computations of second-order low-frequency wave load[C]//Proceedings of the 28th International Conference on Ocean,Offshore and Arctic Engineering.2009:525-532.

[3] CONG P W,GOU Y,TENG B.A new approach to low-frequency QTF and its application in predicting slow drift force[J].Ocean Engineering,2012,53:25-37.

[4] 陈忆宁,陈刚,肖龙飞.浅水 FPSO 二阶力与慢漂阻尼计算分析[C]//第十六届中国海洋 (岸) 工程学术讨论会论文集 (上册).北京：海洋出版社,2013.(CHEN Y N，CHEN G，XIAO L F.Research of second order wave drift force and damping in shallow water[C]//The 16th China Ocean (Shore) Engineering Symposium Proceedings.Beijing:Ocean Press,2013.(in Chinese))

[5] NACIRI M,SERGENT E.Diffraction/Radiation of 135 000 m3storage capacity LNG carrier in shallow water:A benchmark study[C]//Proceedings of the 28th International Conference on Ocean,Offshore and Arctic Engineering.2009:637-647.

[6] 李欣,王磊,杨建民.浅水浮式生产储油系统二阶波浪慢漂力数值计算[J].上海交通大学学报,2006,40(6):997-999.(LI X,WANG L,YANG J M.The numerical calculation on the second order wave drift force of FPSO in shallow water[J].Journal of Shanghai Jiao Tong University,2006,40(6):997-999.(in Chinese))

[7] FONSECA N,PESSOA J,MAVRAKOS S,et al.Experimental and numerical investigation of the slowly varying wave exciting drift forces on a restrained body in bi-chromatic waves[J].Ocean Engineering,2011,38(17):2000-2014.

[8] PESSOA J,FONSECA N.Investigation of depth effects on the wave exciting low frequency drift forces by different approximation methods[J].Applied Ocean Research,2013,42:182-199.

[9] XIAO Longfei ,YANG Jianmin,LI Xin.Shallow water effects on surge motion and load of soft yoke moored FPSO[J].Chinese Ocean Engineering,2007,21(2):187-196.

[10] WANG S Q,LI S Y,CHEN X H.Dynamical analysis of a soft yoke moored FPSO in shallow waters[C]//Proceeding of the 6th International Conference on Asian and Pacific Coasts (APAC).2012.

[11] GUO B,XIAO L F,YANG J M.Analysis on motions and green water of FPSOs in shallow water with non-collinear environments[C]//Proceedings of the 29th International Conference on Ocean,Offshore and Arctic Engineering.2010:419-427.

[12] PHADKE A C,LIAO S,CHEN D,et al.Assessment of SYMS survival limit for “Peng Bo” FPSO during installation[C]//Proceedings of the 29th International Conference on Ocean,Offshore and Arctic Engineering.2010:541-548.

[13] Institute N M T R.SIMO-theory manual[G].Norway:2004.

[14] TENG B,CONG P,GOU Y.Examination on low-frequency QTF of a platform[J].Journal of Hydrodynamics,Ser.B,2010,22(5,Supplement 1):969-974.

[15] Oil Companies International Marine Forum.Prediction of wind and current loads on VLCCs[M].London:Witherby & Co.LTD.,1994.

Investigation of depth effects on the dynamic response performance of soft yoke mooring FPSO

LIU Chengyi1,2,TANG Yougang1,2,LI Yan1,2

(1.Tianjin University,School of Civil Engineering,Tianjin 300072，China；2.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin 300072，China)

P751

A

10.16483/j.issn.1005-9865.2016.01.004

1005-9865(2016)01-0025-08

2014-09-15

国家自然科学基金(51279130)；国家自然科学基金重点项目(51239008)

刘成义(1990-)，男，湖北随州人，硕士，主要研究FPSO系泊系统动力响应。E-mail:liuchengyii@163.com

唐友刚(1952-)，男，教授，博士生导师。 E-mail:tangyougang_td@163.com