腐蚀管道在内压和轴向压力影响下的弯曲破坏

高 杰，李 昕，周 晶

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

腐蚀管道在内压和轴向压力影响下的弯曲破坏

高 杰，李 昕，周 晶

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

运行在恶劣环境中的海底管道，往往受到内压、轴力和弯矩等复杂荷载的联合作用。腐蚀会导致管壁局部变薄，降低管道极限承载力。为保证管道安全高效运行，准确预测和分析复杂荷载作用下的塑性极限承载力和变形行为就显得尤为重要。考虑大应变和大变形、应力强化和材料非线性，运用数值仿真软件建立腐蚀缺陷管道的三维实体有限元模型，在全尺寸管道破坏试验验证的基础上，对腐蚀管道在内压、轴向压力和弯矩相互作用下的失效模式和极限弯矩承载力进行了相关研究，并进行了腐蚀缺陷几何参数的敏感性分析。研究结果表明：初始内压和初始轴向压力会显著降低腐蚀管道的极限弯矩承载力，并且影响最终的失效模式；在腐蚀缺陷几何尺寸参数中，腐蚀宽度比腐蚀深度和腐蚀长度的影响更大。

钢质管道；腐蚀缺陷；数值仿真；复杂荷载；失效模式；极限承载力

Abstract: Offshore pipelines operating in harsh environment are usually subjected to complex combination of bending moment and axial force in addition to internal pressure. Corrosion will lead to local thinning of the pipe wall, thus, ultimate bearing capacity of pipelines with corrosion defects will be reduced. Considering large strains and displacements, stress-stiffening and material nonlinearity, three-dimensional finite element (FE) analyses are carried out to simulate the bending capacity and failure mode of the corroded pipelines with outside locally-thinned-areas (LTAs) subjected to combinations of internal pressure, axial compressive force and bending moment. Additional finite element analyses are then performed to investigate the effect of key parameters, such as wall-thinned depth, wall-thinned angle and wall-thinned length, on maximum moment. The results show that initial internal pressure and initial axial comprehesive force can significantly reduce the ultimate bending capacity of corroded pipes and affect it's failure mode. The corrosion width was proved to have greater influence the corrosion depth and corrosion length on the maximum moment.

Keywords: steel pipe; corrosion defect; numerical simulation; complex load; failure mode; ultimate capacity

海底管道运行在复杂的海洋环境中，往往受到内压、轴力和弯矩等复杂荷载的联合作用。当管道遭受地震、海床变形、滑坡等自然灾害，以及因海床冲刷和淘蚀导致悬空时，弯矩荷载便成为控制管道失效的决定性因素[1]。由于受到输送介质以及海水和土壤中腐蚀物质的腐蚀，管道内壁和外壁会产生局部腐蚀缺陷。腐蚀一方面会引起管壁整体或局部变薄，另一方面会产生应力集中，导致管道的静态和动态抗力减小[2]。

近年来，国内外学者发展了一系列腐蚀缺陷管道剩余强度评价规范。ASME B31G[3]和ASME Code Case N597[4]被广泛用于评价管道的极限承载力，但该规范只适用于因内压引起的管道爆破失效情况。随后DNV RP-F101[5]规范中考虑了轴力和弯矩对管道失效内压的影响，但管道失效形式仍是内压为主的爆破失效。基于塑性上下限理论和Mises屈服准则，Mohareb等[6-11]推导了完好管道在内压、轴力和弯矩联合作用下的极限弯矩荷载解析解。Hauch、Bai等[12-16]将管道的各向异性行为引入该公式，并将其扩展到无限长腐蚀管道中。该方法随后被ABS[17]采用，评估腐蚀管道剩余强度。Chen等[18]基于Hill屈服准则，推导了任意形状腐蚀缺陷管道在内压、轴力和弯矩联合作用下的极限弯矩承载力计算公式。由于理想弹塑性等基本假设的局限，上述理论公式并不能精确预测腐蚀缺陷管道在复杂荷载作用下的极限承载能力。因此，作为一种高效准确的替代方法，有限元数值模拟便得到了广泛应用。

首先运用ABAQUS数值仿真软件建立腐蚀缺陷管道的三维实体有限元模型，通过全尺寸破坏试验验证其准确性。然后采用该模型计算并分析腐蚀缺陷管道在初始内压和轴向压力影响下的极限弯矩承载力和失效模式。最后进行了腐蚀缺陷几何参数的敏感性分析，得到缺陷尺寸对管道极限弯矩承载力的影响程度。

1 有限元模型验证

1.1 全尺寸试验介绍

Yu等[19]开展了一系列轴向腐蚀管道在复杂荷载作用下的全尺寸试验研究。采用四点弯试验装置来进行管道试件的全尺寸破坏试验，试验装置简化模型如图1所示。

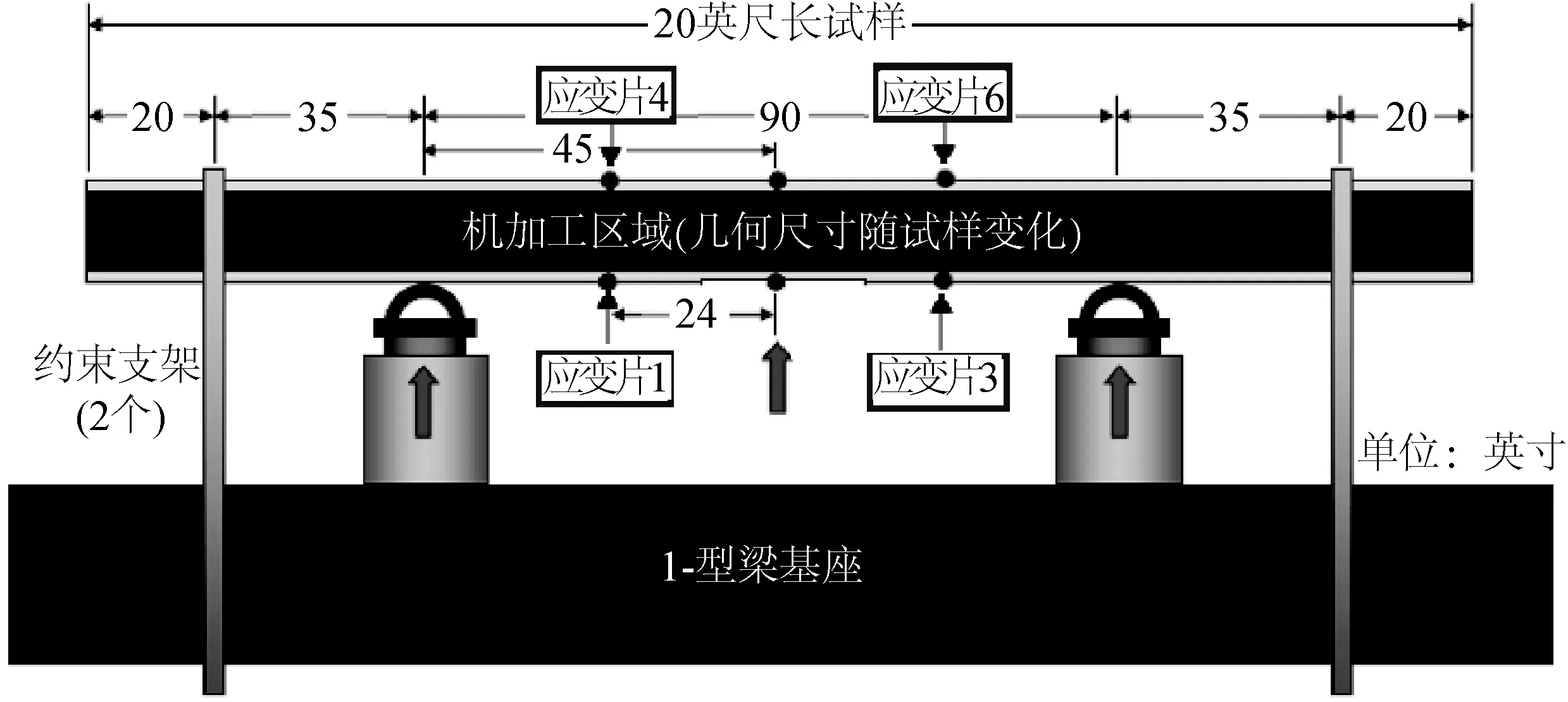
图1 试验装置模型示意Fig. 1 Experimental test program setup

通过关于管道中心截面对称的两个千斤顶来施加对称弯矩。千斤顶之间部分为纯弯段，管道两端可以沿轴向自由变化，故泊松效应产生的轴力由管道的自由伸长抵消，因此轴力只考虑管道与加载装置之间的摩擦，计算公式：

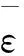
选取试样4试验数据来验证有限元模型的准确性。管道钢型号为API 5L X52，材料屈服强度σy=387.9 MPa，极限抗拉强度σu=502.8 MPa，弹性模量E=207 000 MPa，泊松比ν=0.30，材料曲线如图2所示。

图2 X52钢应力-应变曲线Fig. 2 Stress strain curve from tensile test of X52

图3 腐蚀缺陷管道示意Fig. 3 Pipe specimen with local wall thinning

试样长度为2.286 m，外径D和壁厚t分别为219.1 mm和12.7mm。采用光滑等深度等宽度管壁外腐蚀，腐蚀缺陷由电火花切割加工而成。腐蚀长度L=224.4 mm，腐蚀宽度β=180°，腐蚀深度d=6.35 mm。腐蚀边缘做相应的倒角处理，倒角半径取d/2。腐蚀缺陷管道的几何参数如图3所示。

1.2 有限元模型验证

考虑材料非线性与几何非线性，运用ABAQUS有限元软件建立腐蚀管道的三维有限元分析模型，如图4所示。四点弯加载装置两个千斤顶中间部分为纯弯段，故只需对该部分试件进行有限元模拟即可。考虑施加荷载和结构模型的对称性，选取1/4管道模型进行计算。约束采用对称约束，同时在端部设置参考点，参考点与管道端部截面之间采用MPC绑定，轴力、弯矩以及边界条件均通过参考点施加在管道模型上。选取20节点减缩积分单元(C3D20R)进行模拟计算，可以有效地避免计算过程中的体积自锁现象。

弧长法作为一种广义的位移控制法，能够很好地计算临近极值点时结构的反应和求解结构后屈曲路径的非线性稳定问题[20]，因此文中采用改进Risk弧长法进行极值弯矩的迭代求解。采用数值失稳准则作为管道失效的判别准则，将迭代过程中管道所能承受弯曲力的最大值作为管道的极值弯矩。

图5为试样4的试验失效模式与有限元失效模式对比图。可以看出，有限元计算得到管道失效位置及失效模式与试验结果吻合很好，均为缺陷中部的局部凹陷屈曲。

图4 试样4腐蚀管道实体有限元模型Fig. 4 FE model of Specimen 4

图5 试样4腐蚀管道失效模式Fig. 5 Failure mode of Specimen 4

图6为全尺寸试验和有限元计算得到的整体弯矩—端部转角曲线的对比情况。有限元得到的极限弯矩要略低于试验值，且出现的时刻要略早于试验结果。其中试验极限弯矩为182.10 kN·m，对应的端部转角为0.086 97 rad；有限元极限弯矩为178.28 kN·m，对应的端部转角为0.078 88 rad，误差为-2.14%。两者的整体弯矩—端部转角曲线变化趋势基本相同。

图7为全尺寸试验和有限元计算得到的关键点处应变曲线的对比情况。应变片1与应变片4分别位于管道的受压侧与受拉侧，并且关于管道轴线成对称分布。加载过程中，两个关键点处的有限元值与实验值变化趋势相同，但有限元值整体略大，是由于有限元提取的应变值为点应变，而实验值为局部应变。说明该有限元模型可以较好的模拟腐蚀缺陷管道的变形行为。

通过上述对比分析，验证了所采用有限元模型的准确性，可以用来开展轴向腐蚀管道在初始内压和初始轴力影响下的极限弯曲能力的相关研究。

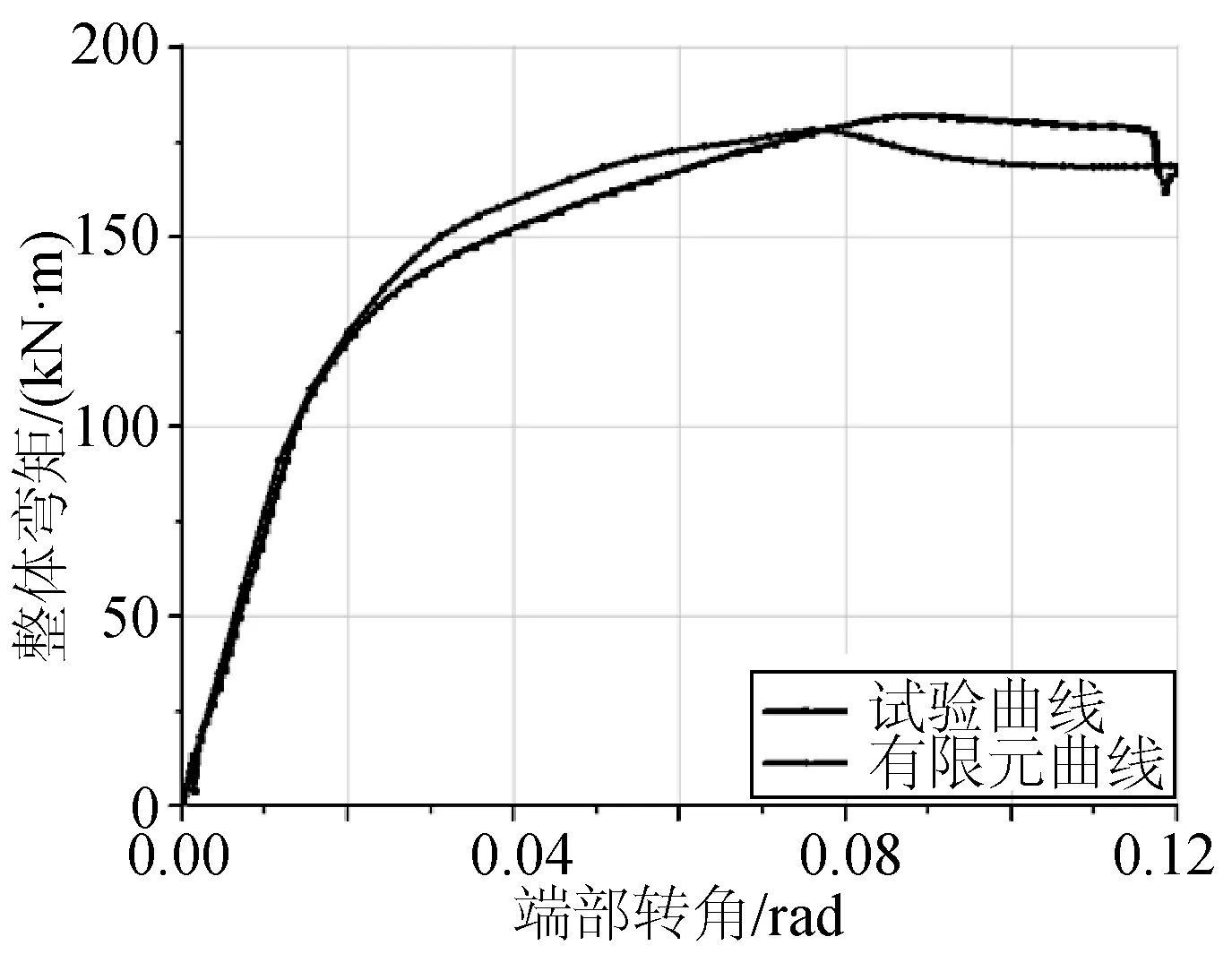
图6 整体弯矩-端部转角曲线Fig. 6 Moment-rotation curve

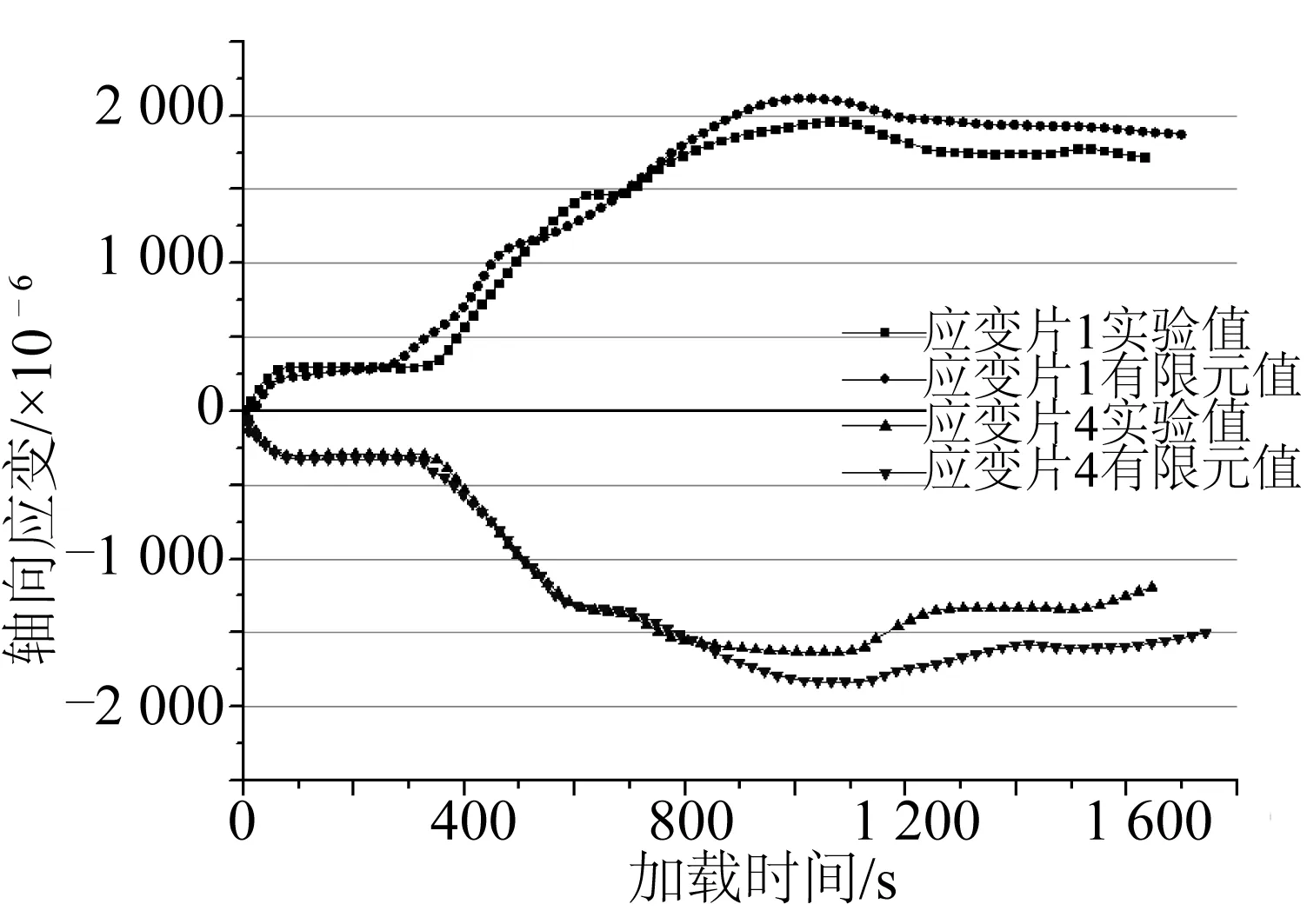
图7 关键点应变值变化曲线Fig. 7 Strain curve for key points

2 初始载荷对腐蚀管道弯曲能力的影响

2.1 计算工况

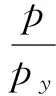
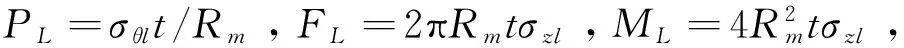
表1 有限元计算工况表Tab. 1 Parameter of finite element model

2.2 初始载荷对腐蚀管道极限弯矩承载力的影响

图8分别给出了工况2和工况4下的内压、轴向压力和极限弯矩相互作用曲面。为了更加直观地分析初始载荷对腐蚀管道极限弯矩承载力的影响，选取工况2来做进一步说明。作出不同Fr下的Mr-Pr曲线如图9(a)，以此分析初始内压对极值弯矩的影响；作出不同Pr下的Mr-Fr曲线如图9(b)，以此分析初始轴向压力对极值弯矩的影响。

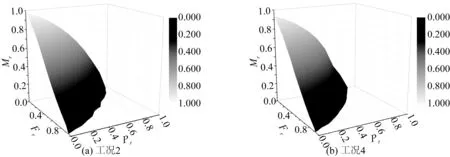
图8 内压、轴向压力和极限弯矩相互作用曲面Fig. 8 Interaction surface for internal pressure, axial comprehensive force and ultimate bending moment

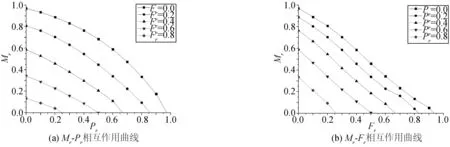
图9 内压/轴向压力和弯矩相互作用曲线(工况2)Fig. 9 Interaction curve between Mr and Pr or Fr

从图8和图9可以看出，初始内压和初始轴向压力均对腐蚀管道的极限弯矩承载力有明显的降低作用，且初始载荷越大，降低作用越明显。图9(a)Fr=0.0时的曲线说明初始内压对极限弯矩的影响是非线性的，影响线近似于1/4圆曲线；而图9(b)Pr=0.0时曲线说明初始轴向压力对极限弯矩的影响近似于线性。当管道在内压、轴向压力和弯矩共同作用时，初始载荷对极值弯矩的影响则是两者的叠加，三者的相互作用曲面为不规则球面，如图8所示。

2.3 初始载荷对腐蚀管道失效模式的影响

管道在内压作用下的失效模式主要是爆破失效，在轴向压力作用下主要是轴向垮塌，在弯矩作用下有整体弯曲、截面椭圆化以及受压侧局部屈曲等多种失效模式，在复杂荷载联合作用下则是以上几种失效模式的叠加。考虑篇幅问题，以工况2所示的缺陷管道为例来详细分析初始载荷对腐蚀管道失效模式的影响。

2.3.1 初始内压对腐蚀管道失效模式的影响

图10给出了腐蚀缺陷管道在不同初始内压影响下达到极值弯矩时的Von Mises等效应力分布云图。管道钢的屈服强度为387.9 MPa，因此云图只显示了Von Mises应力超过屈服强度的部分，即只显示了管道的塑性区域。可以看出初始内压对缺陷管道的最终失效模式有很大影响。当管道不受内压作用时，最终失效模式为腐蚀缺陷边缘的内凹破坏，出现截面椭圆化和局部屈曲；当管道受到内压作用时，其最终破坏形式为腐蚀缺陷部分的外凸破坏，且初始内压越大，外凸构型越明显。当初始内压较小时，腐蚀区域两端应力最大，容易发生塑性破坏；随着初始内压的增大，塑性破坏区域开始往腐蚀区域两侧以及腐蚀区域中部迁移(图中深色部分)。

图11给出了管道失效时缺陷中心处的轴向应力、环向应力以及Mises等效应力随初始内压Pr的变化曲线。可以看出，当内压较小(Pr≤0.4)时，轴向应力绝对值大于环向应力绝对值，轴向破坏起主要作用，管道更易产生受压侧局部屈曲；当内压Pr>0.4时，环向应力绝对值开始明显增长，轴向应力绝对值快速下降，环向应力开始大于轴向应力，环向破坏作用逐渐明显，管道更易发生环向爆破失效，这也更直观地解释了图10所示的变形趋势。

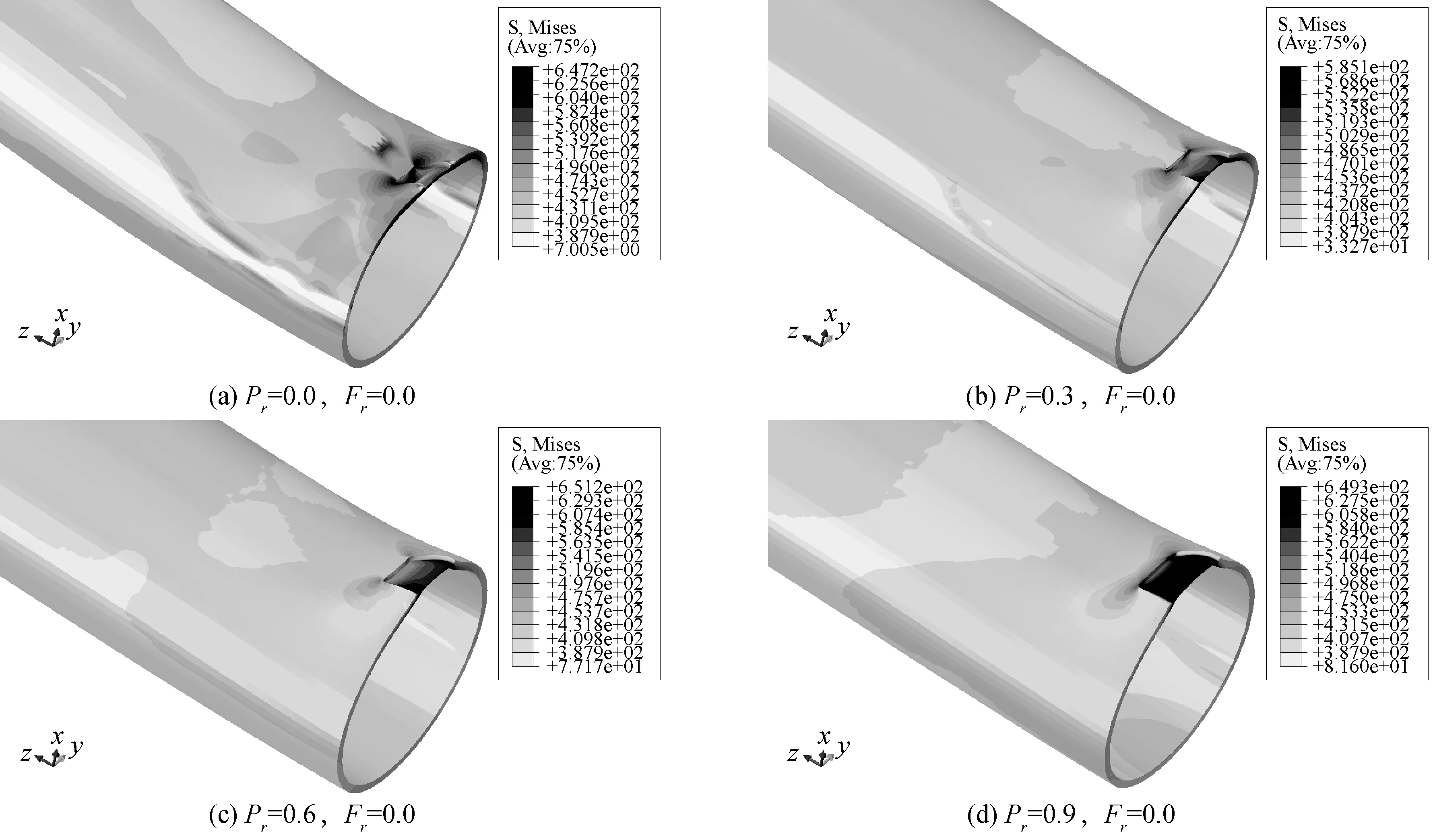
图10 内压、弯矩联合作用下管道Von Mises应力分布Fig. 10 Von Mises stress distribution under the interaction of internal pressure and bending

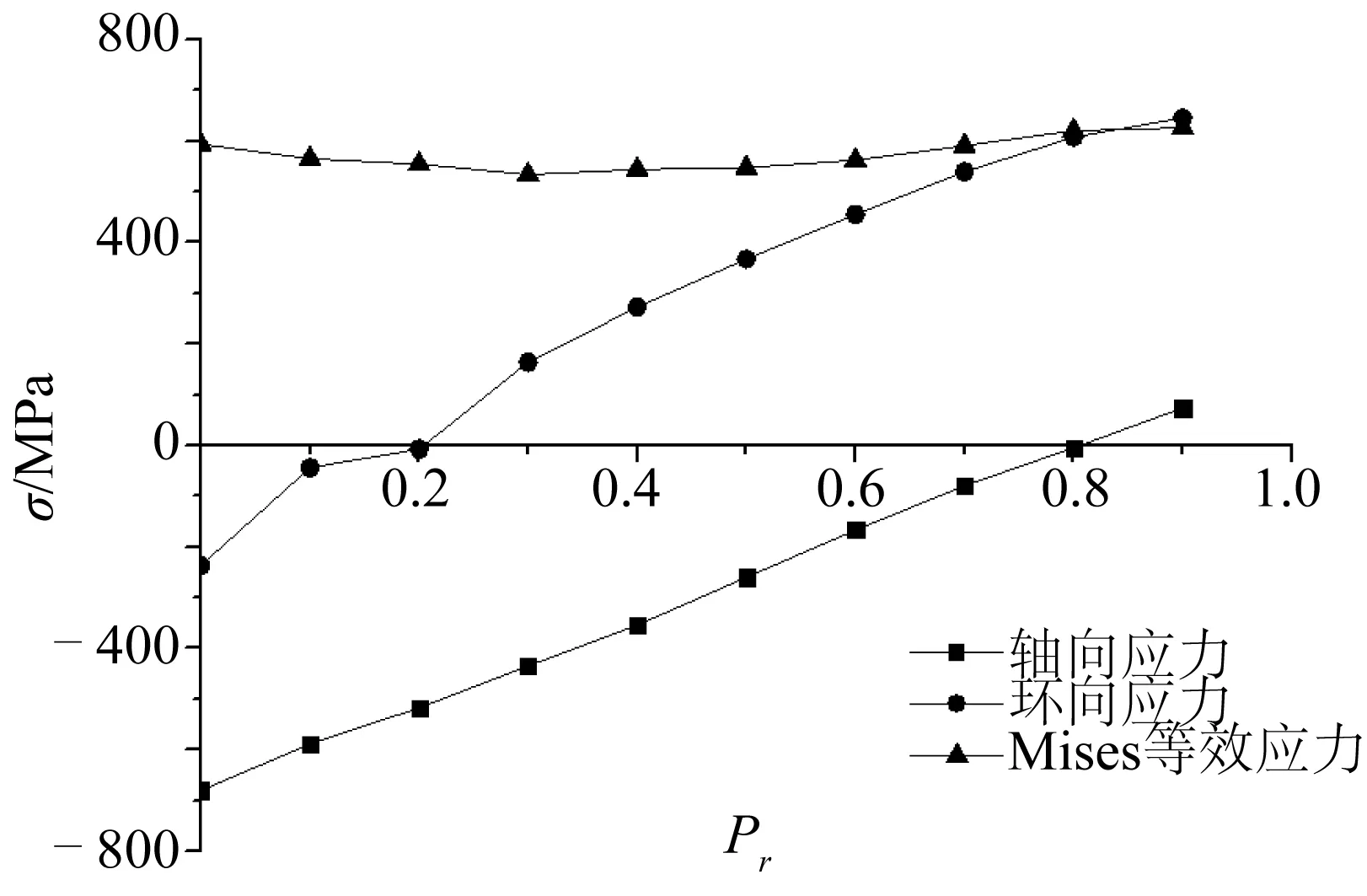
图11 管道失效时缺陷中心应力值随Pr的变化曲线Fig. 11 Curve of stress value in the defect centre with Pr

2.3.2 初始轴向压力对腐蚀管道局部失效模式的影响

图12给出了腐蚀缺陷管道在不同初始轴向压力和弯矩联合作用下的Von Mises等效应力分布云图。可以看出，初始轴向压力对缺陷管道的最终失效模式也有一定的影响。当管道不受轴力作用时，最终失效模式为腐蚀缺陷边缘的内凹破坏，出现截面椭圆化和局部屈曲；当管道受到轴向压力作用时，其破坏构型的内凹程度随初始轴向压力的增大而减小，截面椭圆化和局部屈曲的程度也在减小，更易发生轴向垮塌破坏。无论管道是否承受初始轴向压力作用，应力最大区域均发生在腐蚀缺陷两端，为最易发生破坏区域。

图13给出了管道失效时缺陷中心处的轴向应力、环向应力以及Mises等效应力随初始轴向压力Fr的变化曲线。可以看出，轴向应力绝对值始终大于环向应力绝对值，即轴向压力和弯矩共同作用下轴向应力始终起主要作用；随着Fr的增大，轴向压力引起的轴向应力会逐渐大于弯曲引起的轴向应力，最终失效模式会由局部弯曲垮塌向轴向垮塌过渡。

图12 轴向压力、弯矩联合作用下管道Von Mises应力分布Fig. 12 Von Mises stress distribution under axial compressive force and bending

图13 管道失效时缺陷中心应力值随Fr的变化曲线Fig. 13 Curve of stress value in the defect centre with Fr

3 参数敏感性分析

3.1 腐蚀深度的影响

以工况2、工况3和工况4来分析腐蚀深度对缺陷管道极限弯矩承载力的影响。图14为缺陷管道极限弯矩承载力随腐蚀深度的变化曲线。在所受荷载相同的情况下，随着腐蚀深度的增加，缺陷管道的极限弯矩承载力会随之下降，但是下降幅度并不大，尤其是当腐蚀深度较小的情况下(d/t=0.3和d/t=0.5)。说明对于该尺寸的腐蚀缺陷，腐蚀深度对极限弯矩承载力的影响并不明显。

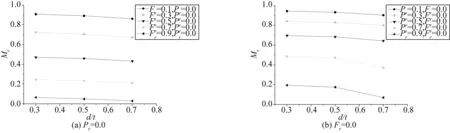
图14 腐蚀深度对极限弯矩承载力的影响Fig. 14 Influence of corrosion depth on ultimate bending moment

3.2 腐蚀长度的影响

以工况1、工况3和工况5来分析腐蚀长度对缺陷管道极限弯矩承载力的影响。图15为缺陷管道极限弯矩承载力随腐蚀长度的变化曲线。在所受荷载相同的情况下，随着腐蚀长度的增加，缺陷管道的极限弯矩承载力也会随之下降，但是下降幅度很小。可以认为腐蚀长度对极限弯矩承载力几乎没有影响，只有在初始内压很大(Pr≥0.9)的情况，腐蚀长度有一定影响。

图15 腐蚀长度对极限弯矩承载力的影响Fig. 15 Influence of corrosion length on ultimate bending moment

3.3 腐蚀宽度的影响

以工况3、工况6和工况7来分析腐蚀宽度对缺陷管道极限弯矩承载力的影响。图16为缺陷管道极限弯矩承载力随腐蚀长度的变化曲线。在所受荷载相同的情况下，随着腐蚀宽度的增加，缺陷管道的极限弯矩承载力会随之下降，下降幅度也很明显。说明腐蚀宽度对缺陷管道的极限弯矩承载力影响较大，应为主要控制参数。

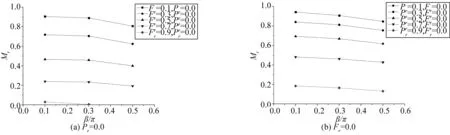
图16 腐蚀宽度对极限弯矩承载力的影响Fig. 16 Influence of corrosion width on ultimate bending moment

4 结 语

应用ABAQUS有限元软件，建立了包含轴向缺陷的腐蚀管道有限元模型，分别计算了多种不同缺陷尺寸的腐蚀管道在内压和轴向压力影响下的极限弯矩承载力，并分析了初始载荷对管道最终失效模式的影响，最后进行了腐蚀缺陷几何尺寸参数的敏感性研究，得到如下结论：

1) 合理的有限元模型可以很好地预测腐蚀管道的极限承载力及其局部变形特性。

2) 初始内压和初始轴向压力会显著降低腐蚀管道的极限弯矩承载力。

3) 初始内压对缺陷管道的最终失效模式有一定影响。不受内压作用时，管道最终失效形式为局部屈曲失效；当管道受初始内压作用时，其最终破坏形式为腐蚀缺陷部分的外凸破坏，更易发生环向爆破失效。

4) 初始轴向压力对腐蚀管道的最终失效模式也有一定影响。当管道不受轴力作用时，最终失效模式为腐蚀缺陷边缘的内凹破坏，出现截面椭圆化和局部屈曲；当管道受到初始轴向压力作用时，截面椭圆化和局部屈曲的程度减小，更易发生轴向垮塌失效。

5) 腐蚀缺陷几何尺寸对缺陷管道在复杂荷载作用下的极限弯矩承载力有一定影响。其中，腐蚀宽度影响最大，腐蚀深度次之，腐蚀长度影响可以忽略。

[1] 陈严飞. 海底腐蚀管道破坏机理和极限承载力研究[D]. 大连: 大连理工大学, 2009. (CHEN Y F. Study on failure mechanism and ultimate load capacity of corroded submarine pipeline[D]. Dalian:Dalian University of Technology, 2009. (in Chinese))

[2] 陈严飞, 李昕, 周晶. 不规则腐蚀缺陷管道极限承载力研究[J]. 工程力学, 2009, 26(11):190-196. (CHEN Y F, LI X, ZHOU J. Ultimate bending capacity of pipe with arbitrary corrosion defects[J]. Engineering Mechanics, 2009, 26(11): 190-196. (in Chinese))

[3] ASMEB31G, Manual of determining the remaining strength of corroded pipelines[S]. A Supplement to ANSI/ASME B31G Code for Pressure Piping, 1991.

[4] ASME Code Case N597, Requirement for analytical evaluation of pipe wall thinning[S]. New York: ASME B&PV Code Sec. XI, Division 1, 1998.

[5] DNV Recommend Practice, RP-F101 Corroded pipelines [S]. Det Norske Veritas, 2000.

[6] MOHAREB M, MURRAY D W. Mobilization of fully plastic moment capacity for pressurized pipes[J]. Journal of Offshore Mechanics and Arctic Engineering, 1999,121:237-241.

[7] MOHAREB M, KULAK G L, ELWI A, et al. Testing and analysis of steel pipe segments[J]. Journal of Transportation Engineering, 2001,127(5):408-417.

[8] MOHAREB M. Plastic interaction relations for pipe sections[J]. Journal of Engineering Mechanics, 2002,128(1):112-120.

[9] OZKAN I F, MOHAREB M. Testing of steel pipes under bending, twist, and shear[J]. Journal of Structural Engineering, 2003,129(10):1350-1357.

[10] MOHAREB M. Plastic resistance of pipe sections: Upper bound solution[J]. Journal of Structural Engineering, 2003,129(1):41-48.

[11] OZKAN I F, MOHAREB M. Testing and analysis of steel pipes under bending, tension, and internal pressure[J]. Journal of Structural Engineering, 2009,135(2):187-197.

[12] HAUCH S, BAI Y. Bending moment capacity of pipes[J]. Journal of Offshore Mechanics and Arctic Engineering, 2000(122):243-252.

[13] BAI Y, HAUCH S R. Analytical collapse capacity of corroded pipes[C]//Proceedings of the International Offshore and Polar Engineering Conference. 1998.

[14] BAI Y, HAUCH S, JENSEN J C. Local buckling and plastic collapse of corroded pipes with yield anisotropy[C]//Proceedings of the International Offshore and Polar Engineering Conference. 1999.

[15] HAUCH S R, BAI Y. Bending moment capacity of groove corroded pipes[J]. International Society of Offshore and Polar Engineers, 2000,122(4): 243-252.

[16] BAI Y, HAUCH S. Collapse capacity of corroded pipes under combined pressure, longitudinal force and bending[J]. International Society of Offshore and Polar Engineers, 2001,11(1):55-63.

[17] ABS, Guide for building and classing subsea pipeline system[S]. Houston: American Bureau of Shipping, 2004.

[18] CHEN Y, ZHANG H, ZHANG J, et al. Residual bending capacity for pipelines with corrosion defects[J]. Journal of Loss Prevention in the Process Industries, 2014,32:70-77.

[19] YU W, VARGAS P M, KARR D G. Bending capacity analyses of corroded pipeline[J]. Journal of Offshore Mechanics and Arctic Engineering, 2012,134:21701.

[20] 朱菊芬，汪海，徐胜利.非线性有限元及其在飞机结构设计中的应用[M]. 上海:上海交通大学出版社, 2011. (ZHU J F, WANG H, XU S L. Nonlinear finite element method and applications in aircraft structural design[M]. Shanghai: Shanghai Jiao Tong University Press, 2011. (in Chinese))

Bending failure of the corroded pipeline subjected to initial internal pressure and axial compressive force

GAO Jie, LI Xin, ZHOU Jing

(State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China)

P756.2; TE973

A

10.16483/j.issn.1005-9865.2016.06.009

1005-9865(2016)06-0074-09

2015-12-01

国家重点基础研究发展计划(973计划)(2011CB013702)；新世纪优秀人才支持计划资助(NCET-11-0051)

高 杰(1988-)，男，山东潍坊人，博士研究生，主要从事海底缺陷管道承载能力的研究。E-mail：gaojie4664@126.com