高温环境中主管轴力对焊接圆钢管T节点承载性能的影响
赵海成,邵永波,杨冬平
(1. 烟台大学 土木工程学院,山东 烟台 264005;2. 西南石油大学 机电工程学院,四川 成都 610500;3. 胜利油田技术检测中心,山东 东营 257062 )
高温环境中主管轴力对焊接圆钢管T节点承载性能的影响
赵海成1,邵永波2,杨冬平3
(1. 烟台大学 土木工程学院,山东 烟台 264005;2. 西南石油大学 机电工程学院,四川 成都 610500;3. 胜利油田技术检测中心,山东 东营 257062 )
利用有限元软件ABAQUS建立T型圆钢管节点热传导分析模型,通过与已有试验数据进行对比,验证了所建有限元模型的可靠性。利用提出的有限元模型分析了不同主管轴力作用下的T型圆钢管节点在火灾环境中的失效过程,研究了主管轴力对T型圆钢管节点临界温度的影响规律。分别讨论了采用屈服强度折减和弹性模量折减的方法预测T型圆钢管节点在高温下的极限承载力,并将预测结果和有限元分析结果进行了对比,给出了这两种方法用于工程设计时的建议。
T型圆钢管节点;主管荷载比;临界温度;极限承载力;有限元分析
Abstract: A finite element model (FEM) of the heat transfer analysis for circular hollow section (CHS) tubular T-joints is built by using software ABAQUS. Through comparison with experimental data, the reliability of the FEM is verified. By using the presented FEM, the failure process of CHS T-joints with different axial forces in the chord in fire condition is analyzed, and the effect of the axial force in the chord of tubular T-joints on the critical temperature is studied. The prediction of the ultimate strength of CHS tubular T-joints at elevated temperature by reduction of the yield strength and reduction of the elastic modulus respectively is discussed, and the predicted results are compared with FE results. Finally, suggestion for design purpose is given.
Keywords: circular hollow section (CHS) tubular T-joint; loading ratio in the chord; critical temperature; ultimate strength; finite element analysis
圆钢管节点由于轻质、高强、施工快捷等优点广泛应用于导管架海洋平台结构中。节点是管结构中传力的关键部位,节点部位破坏会对结构的整体受力性能产生重大影响,因此对空心圆钢管节点的研究具有重要意义。
目前,对于常温下的管节点的力学性能国内外学者做了大量的试验和有限元研究[1-6],对于高温下管节点的静力性能的研究理论主要有两种:瞬态理论与稳态理论。瞬态理论采用恒载升温,而稳态理论则采用恒温加载。由于瞬态理论考虑温度、钢材性能随时间的变化历程,以及火灾发生前节点的初始变形,因此瞬态理论能更好地反映实际火灾发生时的真实外部条件,比稳态理论更具合理性。
高温下管节点静力性能的研究方法主要采用抗火实验和有限元模拟。在稳态理论研究方面,刘明璐等[7]对承受支管轴力的T型圆钢管节点高温下的力学性能进行了研究;Nguyen等[8-11]对承受支管轴力以及承受支管轴力与平面内弯矩共同作用的T型圆钢管节点高温下的力学性能进行了试验研究和数值分析。瞬态理论研究方面,Chen等[12]首次采用瞬态的研究理论对T型圆钢管节点升温条件下的失效过程进行了研究,He等[13]对K型节点在高温下的失效过程进行了试验研究和数值分析。
目前对于管节点抗火性能的分析和研究均忽略了主管轴力的影响。实际的焊接钢管结构,在节点部位,主管一般都主要承受轴向力作用。主管轴力对T节点在火灾环境中临界温度的影响目前尚未见有关的研究成果,因此,这里对主管轴力对焊接圆钢管T节点在火灾环境中临界温度的影响进行了初步研究。
1 高温下T节点有限元模型
有限元建模方法采用间接热力耦合,即先进行热传导分析,导出模型的节点温度,节点温度作为温度荷载导入静力分析模型,并作出以下假设以简化计算:1)不考虑蠕变的影响;2)忽略高温对钢材金相组织的影响;3)管节点均匀受热;4)对流、辐射系数为常数。
1.1 模型几何外形
T型圆钢管节点的几何形状以及尺寸符号如图1所示,其中几个常用的描述管节点几何形状的无量纲参数为:α= 2l0/d0,β=d1/d0,γ=d0/2t0,τ=t1/t0。
1.2 网格方案
热传导分析时网格单元类型采用DC3D8,静力分析时单元类型采用C3D8I,节点区域的网格中单元尺寸为0.01 m,其它区域的网格尺寸为0.02 m,主支管管壁厚度方向网格均采用两层单元,如图2所示。
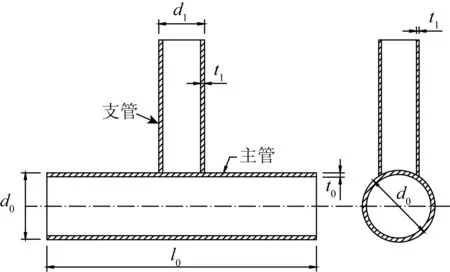
图1 T型圆钢管节点Fig. 1 Circular hollow section T-joint

图2 T型圆钢管节点网格Fig. 2 Mesh of circular hollow section T-joint
1.3 荷载与边界条件

图3 主管端部截面Fig. 3 Top section of chord
T型管节点极限承载力Fu是指T节点最大承载力对应的节点变形与3%d0节点变形的较小值所对应的荷载,本文变形是指冠点与主管两侧最外点之间的位移差,支管端部受压时位移为负。静力分析时支管轴向荷载Fb取只受支管轴力时的T型圆钢管节点极限承载力的0.5倍,施加方式为集中荷载,主管轴向荷载Fc按参数分析的荷载比nc(Fc与主管承受的屈服荷载Fyc(主管横截面面积Ac与主管钢材屈服强度fy乘积)比值取值),施加方式为均布荷载qc=Fc/Ac。主管轴向定义为U3方向,支管轴向定义为U2方向,U1方向垂直于U2、U3,模型的位移边界条件为约束主管两端如图3所示位置(过主管轴线且垂直于U2方向的平面与主管端部截面的交线)的U1、U2方向,约束支管端部U1、U3方向,热传导分析时不对边界进行约束。
1.4 材料与温度参数定义
有限元模型材料密度为7 850 kg/m3、泊松比为0.3、常温下屈服强度为235 MPa、弹性模量为206 GPa,高温下材料的应力应变关、比热、伸长率、导热系数均按EC3-1-2(2005)[14]推荐的公式取值,热传导分析与静力分析材料属性相同。热传导分析时对流和辐射系数分别为25 W/(m2·K)和0.7,外部升温曲线取标准升温曲线即ISO834火灾曲线。
1.5 有限元模型验证
为了保证有限元模型在分析管节点抗火性能方面的可靠性,以便用于后面的参数分析,首先对有限元模型的准确性进行验证。利用提出的有限元模型,对Chen等[12]的试验测试结果进行了有限元模拟,试件的材料属性、边界条件及施加荷载等均与文献[12]中的相同,计算得到的温度-时间曲线和位移-温度曲线对比分别如图4和图5所示,图中对比的各个测点位置可参考文献[15]中的定义。
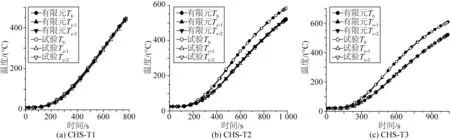
图4 温度-时间曲线Fig. 4 Temperature-time curves
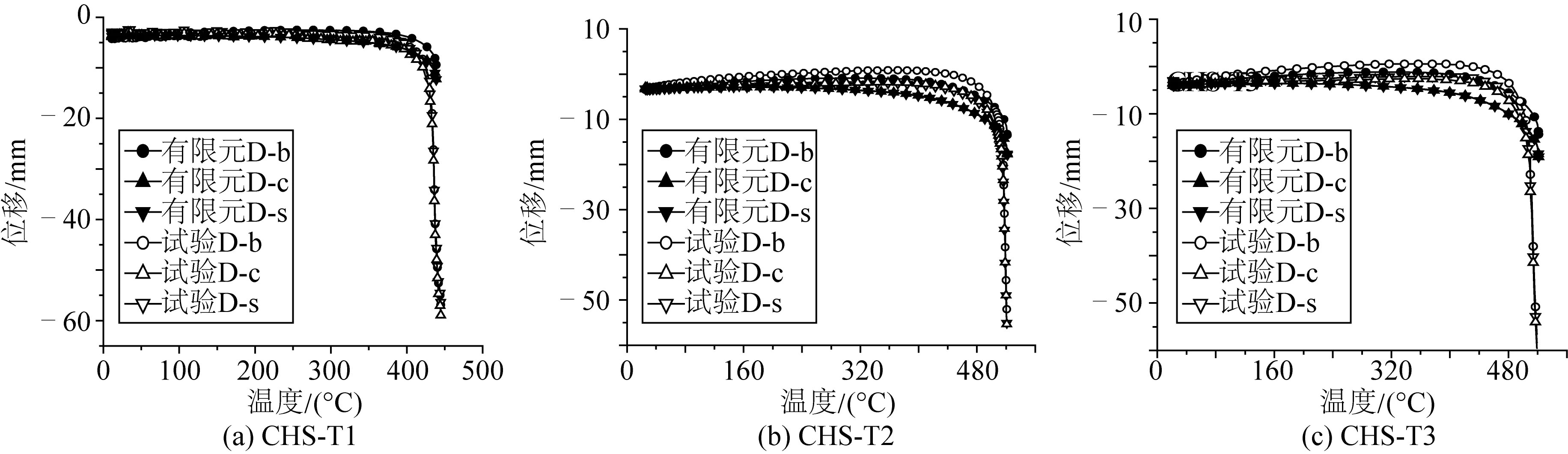
图5 位移-温度曲线Fig. 5 Displacement-temperature curves
通过有限元与试验结果的对比分析可以发现,有限元模型可以准确地模拟试件温度测点的升温过程以及测点位移随温度的变化规律。由于有限元模拟与试验时的复杂边界不能完全一致,位移-温度曲线模拟会有微小差别。但是有限元分析结果对T节点失效过程的模拟是准确可靠的,其精度可以得到保证,所以有限元模型可以用于T节点抗火性能分析。
2 主管轴力对T节点临界温度影响的参数分析
为了研究主管端部轴力大小对T节点在升温过程中的临界温度的影响,对表1所示的12个T节点模型在火灾环境下的升温过程进行了模拟,其中,nb=Fb/Fu,nc=Fc/Fyc=qc/fy。表1中的12个T节点模型主要考虑支管和主管直径比参数β的取值不同、主管直径和2倍主管壁厚比参数γ的取值不同,这是因为以往的文献及有关规范规程中对管节点承载力计算方法中均根据β、γ不同而考虑不同的节点失效模式。表1中的主管轴力比参数nc取值为正表示压力,负值则表示主管承受轴向拉力。

表1 T型圆钢管节点几何尺寸Tab. 1 Geometric dimensions of circular hollow section T-joint
2.1 极限承载力的确定

图6 荷载-变形曲线Fig. 6 Load-deformation curves
T节点在支管轴力作用下极限承载力Fu根据荷载-变形曲线确定。图6所示为β=0.4,γ=18和β=0.7,γ=18以及β=0.4,γ=27时的无主管轴力的模型的荷载-变形曲线。从图中可看出:荷载-变形曲线中均有明显的峰值点,而且峰值点位置在3%d0变形限值之前,所以节点极限承载力根据曲线中的峰值点确定,即三个模型的极限承载力分别为166.6 kN、237.4 kN、86.3 kN。
2.2 温度-变形曲线
表1中的有限元模型根据参数β、γ的取值不同分为三组:第一组模型的β=0.4、γ=18;第二组模型的β=0.7、γ=18;第三组模型的β=0.4、γ=27。三组模型的温度变形曲线如图7所示。

图7 变形-温度曲线Fig. 7 Deformation-temperature curves
根据图7可以看出:在升温的初始阶段,T节点变形很小,当温度超过一个临界值时,在很小的温度区间内管节点的变形急剧增大,此时节点进入失效阶段。从变形过程看,对于β值较小的模型(β=0.4),总体上在节点发生失效的过程中,变形有一段明显缓慢增加的阶段,表现在在相同温度时第一组节点模型的变形值明显大于第二组。这主要是由于在β值较小时,支管直径相对于主管直径更小,所以支管和主管相贯线更短,支管和主管之间的接触面积更小。因此在承受支管传递来的轴力作用时,相贯线部位的应力集中更大,主管更容易发生局部变形。从第一组和第三组结果看:参数γ对T节点失效过程影响较小,节点达到相同大小的变形时,对应的温度非常接近,所以可以认为主管径厚比参数γ对T节点在高温下发生失效时的临界温度影响不大。
2.3 临界温度的定义
临界温度可定义为管节点进入失效时的温度。对于管节点失效的定义,在高温下没有普遍接受的定义。在常温状态,一般按照图6所示的方法定义极限荷载和失效状态,其中3%d0变形限值是由Lu[1]提出的。但He[13]通过研究发现这种用于定义常温下管节点临界状态的方法在定义高温状态下极限状态时偏于危险,并提出变形速率的方法确定临界温度,即将变形速率k=0.1 mm/℃时的温度定义为临界温度。根据这个定义,表1中T节点有限元模型的临界温度可以从温度-变形曲线中得到,结果如表2所示。
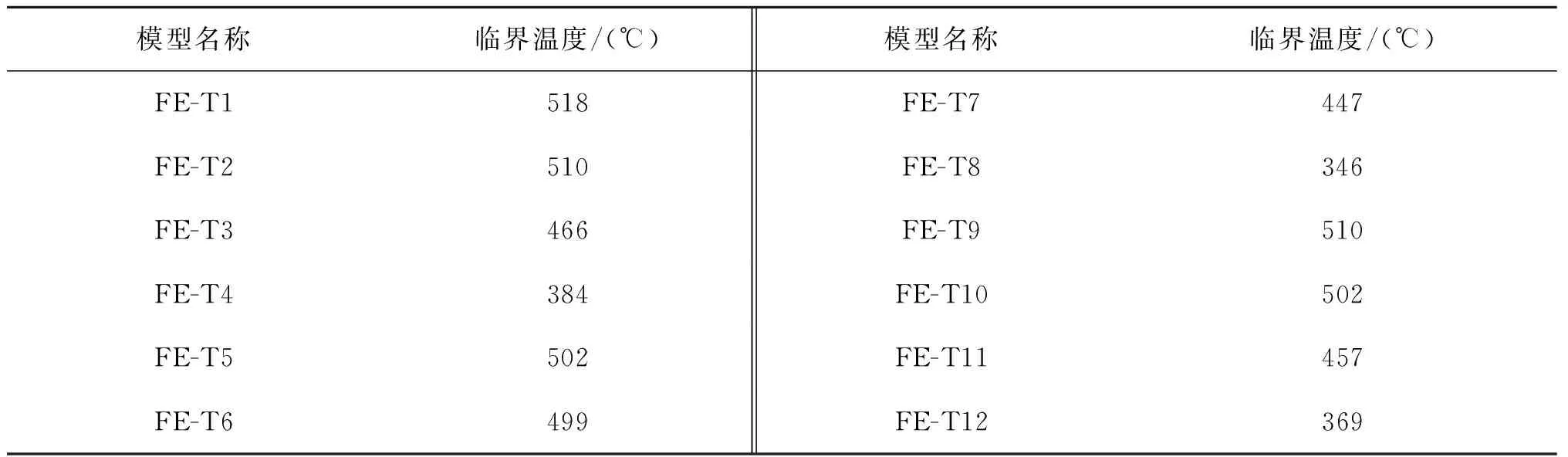
表2 T型圆钢管节点临界温度Tab. 2 Critical temperature of circular hollow section T-joint

图8 模型临界温度Fig. 8 Critical temperature of model
2.4 模型参数对临界温度的影响规律
为了研究便于比较分析主管轴力对临界温度的影响规律,将表2中各模型的临界温度绘于图8,由图8可以发现以下规律:1)对于β相同的T节点,主管承受轴向拉力时,节点的临界温度略有提高,但该有利影响很小,基本可忽略不计。2)主管承受轴向压力时,节点临界温度随主管轴力比参数nc的增加明显降低,并且降低速度加剧;3)T节点β越大,nc对T节点临界温度的影响越明显;相同主支管荷载比的T节点,β越大临界温度越低。4)参数γ对临界温度的影响不显著。
3 高温下考虑主管轴力的T节点承载力
3.1 常温下管节点承载力计算方法
EC3-1-8(2005)[16]中给出了常温下T型节点的静力承载力,计算公式:
其中,γM5=1,fy0表示材料常温下的屈服强度,σ0,Ed表示主管初始轴向应力,kp≤1,受拉时取kp=1,对于T节点,θ1=90°。
3.2 高温下管节点承载力计算方法
目前,高温下T节点的静力承载力的计算方法有两种:第一种是屈服强度折减法,将式(1)中fy0均乘以高温下材料屈服强度的折减系数,第二种是弹性模量折减法,将式中fy0均乘以高温下材料弹性模量的折减系数。因此高温下T节点的静力承载力可由常温下的静力承载力乘以综合折减系数(包含fy0折减以及fy0折减引起的kp折减)求得,本文模型计算结果列于表3。

表3 高温下T节点极限承载力Tab. 3 Ultimate strengths of T-joints

图9 模型λE值Fig. 9 Value of λE
FFE表示有限元模型模拟值,Fuy表示按屈服强度折减计算值,FuE表示按弹性模量折减计算值。由表3可知,采用弹性模量折减的计算方法具有较高准确性,为了方便评价这种方法的安全性引入比例系数λE,λE=FuE/FFE,有限元模型的λE值如图9所示。
3.3 高温下管节点承载力设计建议
由图9可以发现,采用弹性模量折减方法计算T节点高温下的极限承载力,计算结果偏于危险,为了可应用于工程设计,需要对计算结果进行修正。由于λE介于1.05至1.2之间,因此可以引进修正系数k,k=1/1.2,为了方便计算取k等于0.85。高温下T节点的极限承载力Fu计算公式:
为验算公式的精度,将采用式(2)计算的极限承载力值Fu以及有限元模拟值FFE分别列于表4。
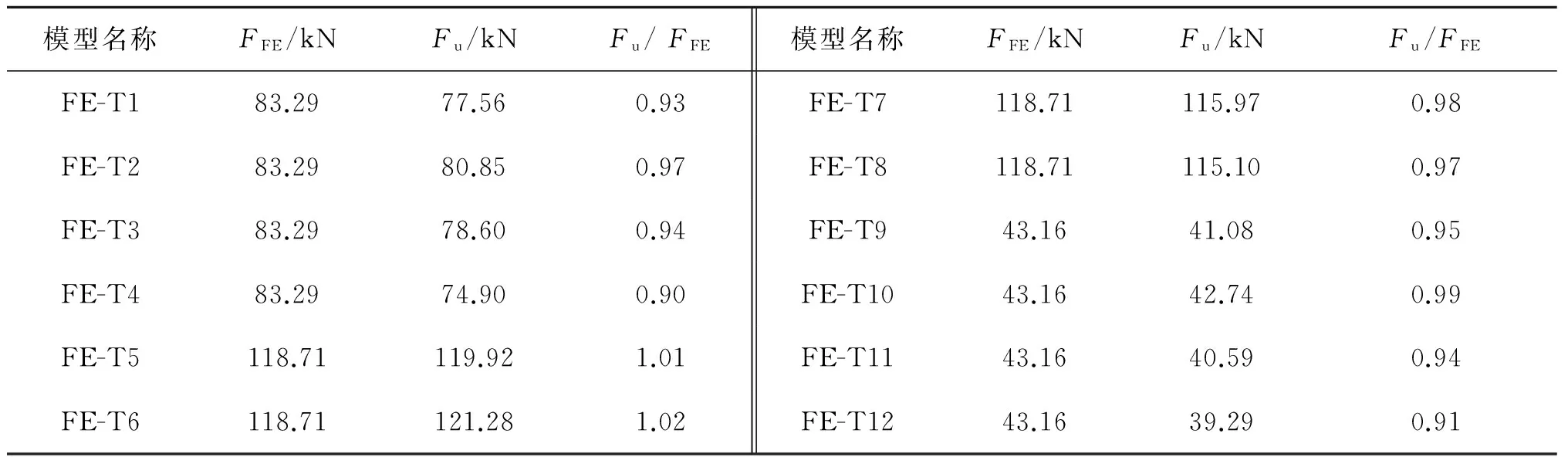
表4 极限承载力修正计算值与有限元模拟值的比较Tab. 4 Comparison of ultimate strengths from calculation and finite element models analyses
由表4数据可以发现,采用式(2)计算T型圆钢管节点高温下的极限承载力时,计算结果具有较高准确性,误差在9%以内,且具有较高的安全性,Fu/FFE均小于1.02。
4 结 语
通过以上分析可以得出以下结论:
1)T型圆钢管节点主管承受轴向拉力时,节点的临界温度略有提高,主管承受轴向压力时,节点临界温度随nc的增加明显降低,并且降低速度加剧。
2)高温下T型圆钢管节点的极限承载力可以采用弹性模量折减的方法计算,并取k=0.85进行修正。
[1] LU L H, DE WINKEL G D, YU Y, et al. Deformation limit for the ultimate strength of hollow section joints[C]//Proceedings of the 6th International Symposium on Tubular Structures. 1994: 341-348.
[2] 陈以一, 沈祖炎, 詹琛,等. 直接交汇节点三重屈服线模型及试验验证[J]. 土木工程学报, 1999,32(6): 26-31. (CHEN Yiyi, SHEN Zuyan, ZHAN Chen, et al. Three lines limit-analysis model for CHS K-joints and its verification by tests[J]. China Civil Engineering Journal, 1999, 32(6): 26-31. (in Chinese))
[3] 陈以一, 陈扬骥, 詹琛, 等. 圆钢管空间相贯节点的实验研究[J]. 土木工程学报, 2003, 36(8): 24-30. (CHEN Yiyi, CHEN Yangji, ZHAN Chen, et al. Experimental research on multi-planar joints of steel tubular members[J].China Civil Engineering Journal, 2003, 36(8): 24-30. (in Chinese))
[4] SHAO Y B. Geometrical effect on the stress distribution along weld toe for tubular T-and K-joints under axial loading [J]. Journal of Constructional Steel Research, 2007, 63: 1351-1360.
[5] SHAO Y B, LIE S T, CHIEW S P. Static strength of tubular T-joints with reinforced chord under axial compression[J]. Advances in Structural Engineering, 2010, 13(2): 369-377.
[6] KIM J W, KIM S S, LEE M J, et al. Vierendeel joints in the circular hollow sections of high strength steel subjected to brace moment and chord compressive loadings[J]. International Journal of Steel Structures, 2012, 12: 579-587.
[7] 刘明璐, 赵金城, 杨秀英, 等. 海洋平台T型相关节点抗火性能研究[J]. 海洋工程, 2009, 27(3): 6-13. (LIU Minglu, ZHAO Jincheng, YANG Xiuying, et al. Study on mechanical performance of tubular T-joints of offshore platform under fire[J]. The Ocean Engineering, 2009, 27(3): 6-13. (in Chinese))
[8] NGUYEN M P, FUNG T C, TAN K H. An experimental study of structural behaviours of CHS T-joints subjected to brace axial compression in fire condition[J]. Tubular Structures XIII. Hong Kong, 2010: 725-732.
[9] NGUYEN M P, TAN K H, FUNG T C. Numerical models and parametric study on ultimate strength of CHS T-joints subjected to brace axial compression under fire condition[J]. Tubular Structures XIII. Hong Kong: CRC Press/Balkema; 2010: 733-740.
[10] NGUYEN M P, FUNG T C, TAN K H. Performance of CHS T-joints in a standard fire test[J]. Tubular Structures XIV. London, 2012: 599-606.
[11] NGUYEN M P, FUNG T C, TAN K H. Structural behavior of CHS T-joints subjected to brace in-plane bending at elevated temperatures[J]. Tubular Structures XIV. London, 2012: 607-614.
[12] CHEN C, SHAO Y B, YANG J. Experimental and numerical study on fire resistance of circular tubular T-joints[J]. Journal of Constructional Steel Research, 2013: 85:24-39.
[13] HE S B, SHAO Y B, ZHANG H Y, et al. Experimental study on circular hollow section (CHS) tubular K-joints at elevated temperature[J]. Engineering Failure Analysis, 2013, 34: 204-216.
[14] EN 1993-1-2, Eurocode 3: Design of steel structures—Part 1-2:General rules—Structural fire design[S].UK: British Standards Instiutions, 2005.
[15] 陈成. 焊接圆钢管节点抗火性能研究[D]. 烟台: 烟台大学, 2013. (CHEN Cheng. Fire resistance of welded circular tubular joints[D]. Yantai: Yantai University, 2013. (in Chinese))
[16] EN 1993-1-8, Eurocode 3: Design of steel structures—Part 1-8: Design of joints[S].UK: British Standards Instiutions, 2005.
Effect of axial force in the chord on the performance of circular tubular T-joints at elevated temperature
ZHAO Haicheng1, SHAO Yongbo2, YANG Dongping3
(1. School of Civil Engineering, Yantai University, Yantai 264005, China; 2. School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China; 3. Technology Inspection Center, China Petroleum & Chemical Corporation, Dongying 257062, China)
P751; TE973
A
10.16483/j.issn.1005-9865.2016.06.013
1005-9865(2016)06-0111-07
2015-12-06
邵永波(1973-),山东海阳人,教授,主要从事工程结构的力学分析方法的研究。E-mail: ybshao@swpu.edu.cn

