失效树在连续刚构桥体系可靠度中的应用

彭子茂

(湖南交通职业技术学院，湖南 长沙　410132)



失效树在连续刚构桥体系可靠度中的应用

彭子茂

(湖南交通职业技术学院，湖南 长沙410132)

基于连续刚构桥破坏机制及失效准则，采用全局临界强度分枝-约界准则作为结构的失效模式，并通过JC法计算结构失效可靠指标，提出了连续性刚构桥界结构体系的可靠性计算过程。以工程实例分析了构件的失效形式及顺序，建立了失效树，并对可靠性指标、概率以及结构可靠性进行了计算。应用表明主桥结构比桥墩容易失效，该可靠性的计算过程能够可靠便捷地体现连续刚构桥结构体系可靠性。

；连续刚构桥；失效树；可靠度

0　前言

连续刚构桥是在我国应用极为广泛的一种桥梁，由于其独特之处，为我国桥梁的建造带来了非常大的经济效益和社会效益。该种桥型由于桥墩固结，梁体连续的特点，因此，该桥型既具有无伸缩缝和行车平顺的优点，而且具有不设支座和无需转换体系的特点。这种结构桥梁能够简化施工，在顺桥向、横桥向分别具有较大的抗弯和抗扭刚度，且可以适应于大跨度桥梁[1]。

桥梁结构构件渐变失效引起结构体系失效，不同类型和顺序的失效产生了不同的失效模式，失效形成的路径也具有不唯一性。目前，结构体系的失效概率的计算方法多种多样，而其应用还不成熟。利用有限元分析手段来得到失效模式的方法主要运用在建筑结构中，桥梁中的应用也大都集中于连续梁桥，而在连续刚构桥中的应用很少[2-4]，因此，找到结构的失效模式是连续刚构桥设计和可靠性分析中的一个关键点[5，6]。基于可靠度理论，应用概率分析的方法对连续钢构桥梁可靠性设计进行分析。将进一步推进大跨径桥梁的可靠度设计进展，提高结构设计的安全性及促进经济技术效益的发挥。

国内外研究人员对桥梁结构构件可靠度计算开展了大量的工作，基本达成了统一的共识，实现了量化计算。对于桥梁结构构件可靠度的计算方法多种多样，而JC法最为简易，且精度可以符合规范的要求，被广泛的运用。对比来讲，结构体系可靠度分析方法更为全面，但往往在实际中运用比较困难，特别是在桥梁可靠度分析中的应用。大量的研究文献表明，桥梁结构体系可靠度的研究都是通过桥梁构件的可靠指标来反映整体桥梁体系的可靠度，而实际上桥梁结构体系可靠度不能完全依据关键构件的最低可靠度指标来反映，需要进行特定的研究[7]。综上所述，本文将以某连续刚构桥为例，对桥梁结构体系的可靠度进行研究。

1　连续刚构桥失效机理及模式

1.1失效机理

依据桥梁运营期的特点和需求，对连续刚构桥的破坏准则进行定义：一旦桥梁的任意桥跨产生相当量的塑性铰而形成破坏结构，那么可以认为桥梁整体遭到破坏[8]。通常连续梁内可能产生的失效截面将对应多个塑性铰。

连续刚构桥属于超静定结构，在外力作用下，即使某截面出现塑性铰，连续钢构桥依然能够承受荷载而不会立马破坏。通常塑性铰截面上的弯矩达到极限，随着荷载作用的增加，该界面的弯矩大小不发生变化，而弯矩方向产生转动，随即产生其他的塑性铰，最终变为可变结构。连续桥梁的失效形式与钢架结构的失效形式相似。单跨钢架结构的失效如图1。

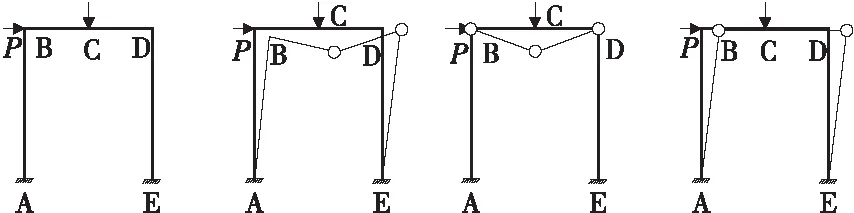
图1　单跨钢架结构失效图

1.2失效路径的查找

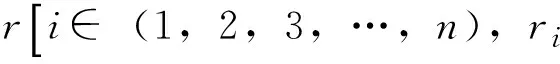
(1)

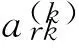
全局临界强度分枝-约界法与下面的复合操作相同。在结构体系失效的第k个阶段中，考虑复合约界条件，如下：

(2)

当结构单元满足式(2)时，即可进行下一步，预先筛选出失效单元；当不满足时，那么可不考虑该情况下的失效树分支。若进入失效过程的第k步，包括可能失效的单元NK个，通过循环可能失效的单元，即可得到下一步可能失效单元序列，周而复始，直至满足失效标准为止。

得到的每一个失效模式，将通过调整柔性控制边界。当满足如式(3)：

(3)

即取：

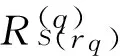
(4)

若不满足，则保持不变。

一般认为，当平均临界强度小于该最小值约1.2倍时，失效模式对结构体系的总体失效概率的影响很大，反之则可忽略失效模式，所以，CS取1.2时可符合要求。

1.3主要失效模式的识别

通过分局分枝—约界准则来判断体系主要的失效模式，并画出能够描述结构体系失效路径的失效树，图2即为连续刚构桥的主要失效模式的判断流程图。

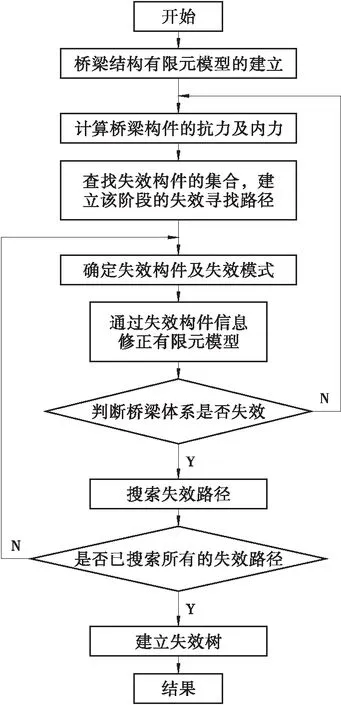
图2　连续刚构桥主要失效模式的判断流程图

2　结构体系可靠度分析

连续刚构桥结构体系可靠度分析步骤：

1) 分析桥梁的有限元模型的建立，并通过软件计算该桥梁结构抗力和荷载作用。

2) 依据有限元模型得到各个截面的抗力大小，同时联合内力值运用全局临界强度分枝—约界法判断桥梁体系的主要失效模式，画出桥梁体系的失效树。

3) 通过失效树可以得到体系的主要失效模式，利用JC法计算体系的失效概率和可靠度指标。

连续刚构桥体系的可靠度分析流程如图3所示。

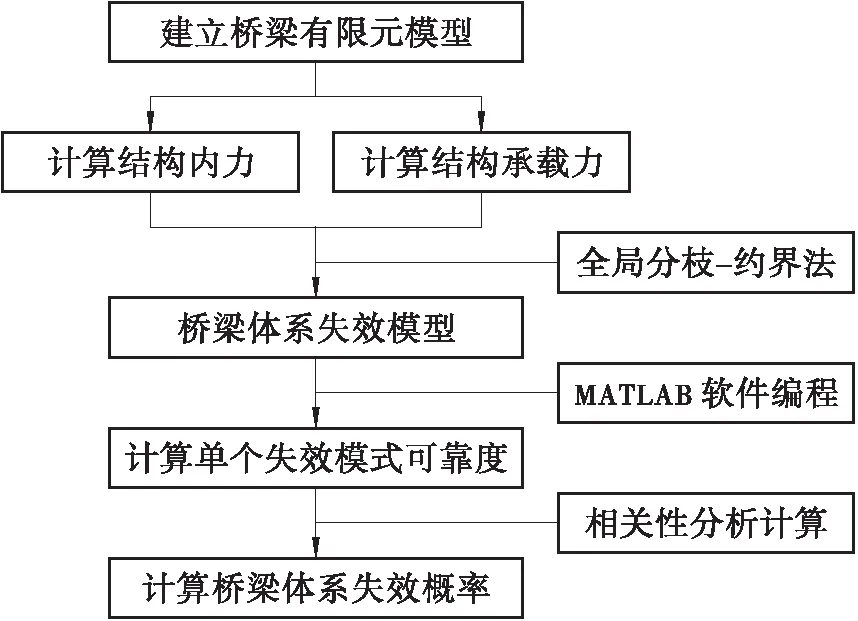
图3　连续刚构桥可靠度计算过程

3　工程实例分析

3.1工程概况

某4跨对称的预应力连续刚构桥的跨径形式为90 m+170×2 m+90 m，桥墩高为30 m。箱梁为变截面预应力混凝土单箱单室结构，采用C55混凝土，顶宽为12 m，箱体宽6.5 m，跨中截面梁高3.0 m，其余截面梁高按二次抛物线分布；桥墩采用钢混空心薄壁墩，采用C40混凝土；预应力为纵、竖双向体系，预应力钢绞线的抗拉强度标准值为1 860 MPa。

3.2建立失效树

依据有限元计算结果，对半桥的120个箱梁截面的内力数据进行分析，通过分枝-约界准则来寻找桥梁体系的失效模式。依据连续钢构桥的破坏机制及失效准则，并考虑到连续刚构桥跨中和边跨的失效情况。

表1例举了该桥主梁的边跨的部分箱梁截面在第1阶段失效过程中的内力计算结果。

其他失效截面均依据最小荷载增量比进行查找，得到第1级失效截面分别为主梁边跨25#截面、中跨79#截面、边跨桥墩175#截面以及跨中桥墩187#截面，并在有限元中将这些截面视为失效，不再进行下一阶段的计算。继续搜寻得到第2级和第3级失效单元，那么可以得到结构体系的失效过程的主要失效模式，如表2所示。失效模式一列中的数字编码表示每一级的失效截面，将跨中截面得到的3级失效截面形成一组失效模式，边跨搜寻得到2级失效截面形成一组失效模式。

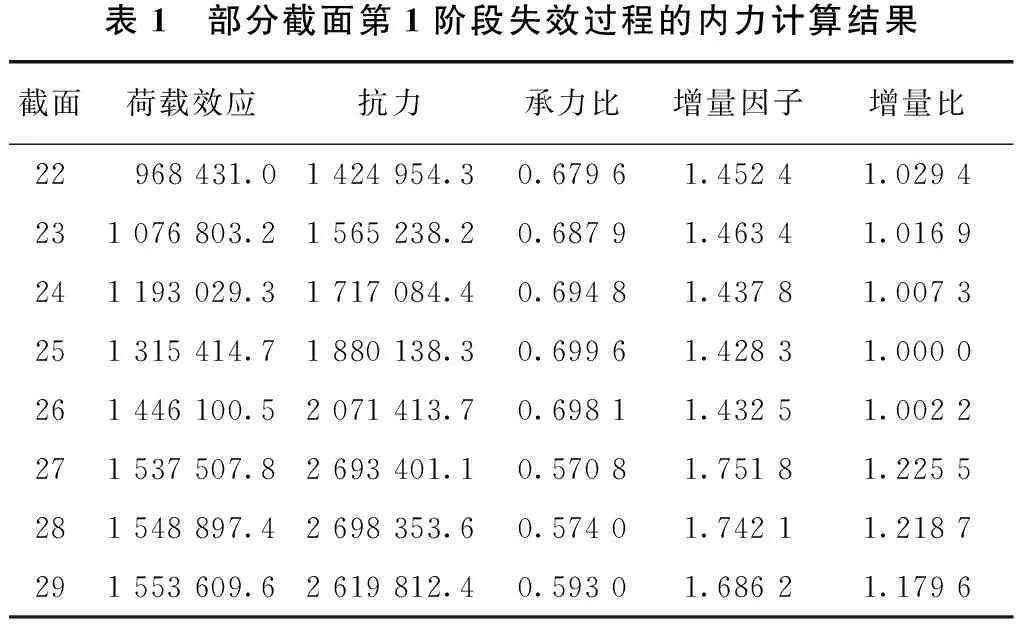
表1 部分截面第1阶段失效过程的内力计算结果截面荷载效应抗力承力比增量因子增量比22968431.01424954.30.67961.45241.0294231076803.21565238.20.68791.46341.0169241193029.31717084.40.69481.43781.0073251315414.71880138.30.69961.42831.0000261446100.52071413.70.69811.43251.0022271537507.82693401.10.57081.75181.2255281548897.42698353.60.57401.74211.2187291553609.62619812.40.59301.68621.1796

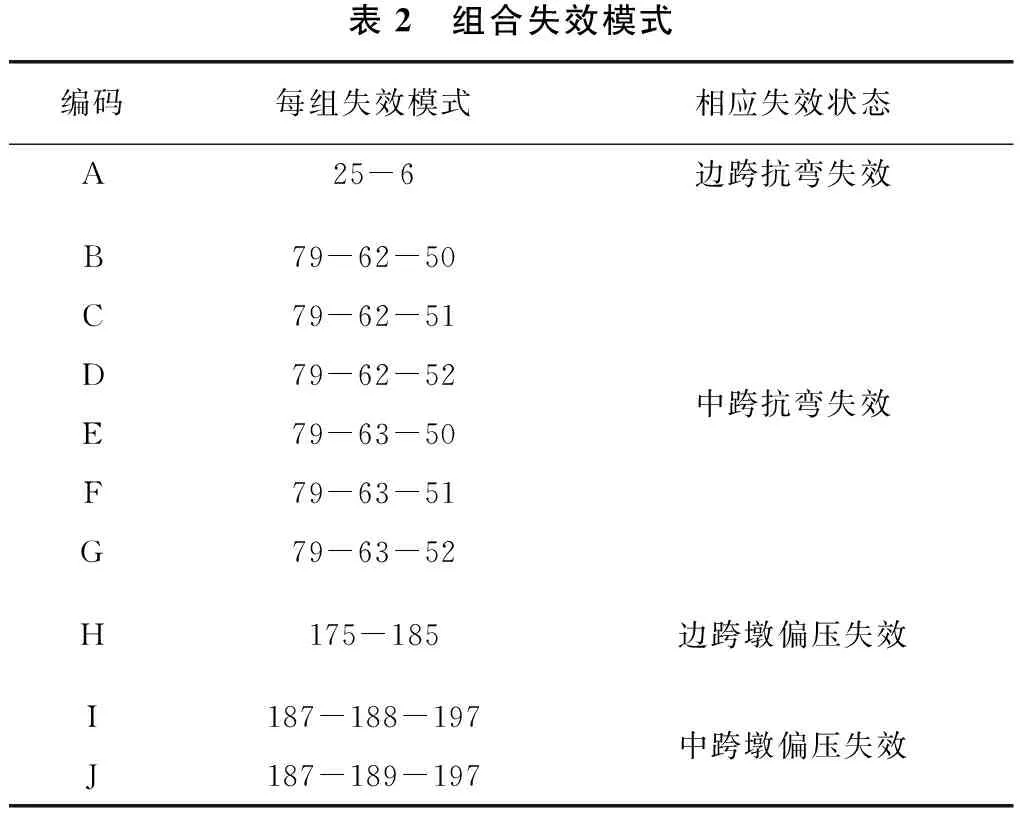
表2 组合失效模式编码每组失效模式相应失效状态A25-6边跨抗弯失效B79-62-50C79-62-51D79-62-52E79-63-50F79-63-51G79-63-52中跨抗弯失效H175-185边跨墩偏压失效I187-188-197J187-189-197中跨墩偏压失效

通过归纳该连续刚构桥结构体系的失效模式，建立连续刚构桥的失效树，如图4。

该连续刚构桥存在的可能半桥失效截面，见图5中的数字编码。

3.3结构可靠指标及可靠度

结构极限状态方程为R-SG-SQ=0，并将结构抗力R、荷载效应的标准值SG和SQ与统计值的乘积当做结构抗力及荷载作用效应分布函数值，再结合JC法的计算程序，运用MATLAB处理软件编程得到每组失效模式的可靠性指标β，结果如表3所示[11，12]。

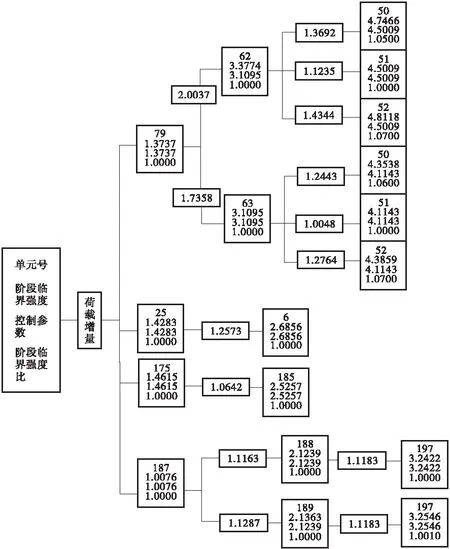
图4　连续刚构桥的失效树

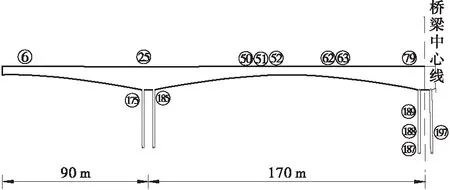
图5　连续钢构桥半桥失效截面

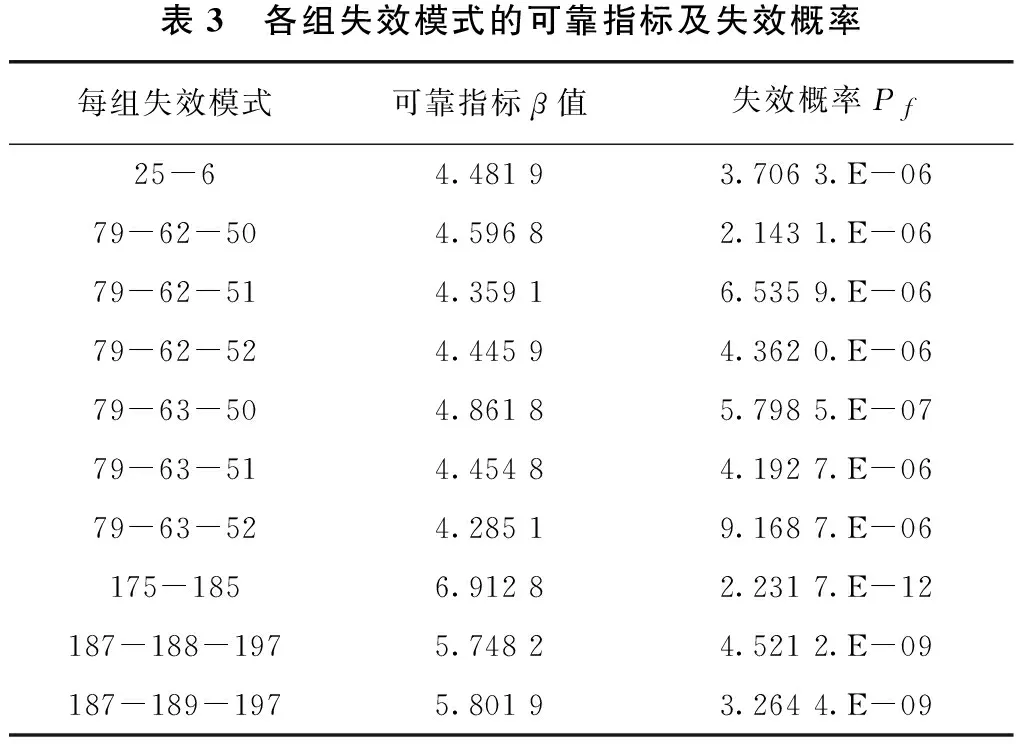
表3 各组失效模式的可靠指标及失效概率每组失效模式可靠指标β值失效概率Pf25-64.48193.7063.E-0679-62-504.59682.1431.E-0679-62-514.35916.5359.E-0679-62-524.44594.3620.E-0679-63-504.86185.7985.E-0779-63-514.45484.1927.E-0679-63-524.28519.1687.E-06175-1856.91282.2317.E-12187-188-1975.74824.5212.E-09187-189-1975.80193.2644.E-09

各个模式之间的相关程度用相关系数表示，结果见表4。通过每组失效模式之间的联系的物理关系，来简化连续刚构桥可靠性指标的计算。模式之间联系的物理量即相关系数，各失效模式间的相关系数见表4所列。由表4计算结果看出，各个失效模式之间的相关系数都靠近1，表明各个失效模式之间的相关度极高。

结合各个失效模式小的可靠性指标β及模式间的相关系数，通过计算可以得到失效模式的失效概率大小及体系可靠指标。将相关系数0.9视为临界值，同时由于各失效模式之间的相关程度很高，因此，采用PENT法[13，14]计算连续刚构桥体系的综合失效概率和相对应的体系可靠指标，即Pf为9.168 7E-06，βs为4.285 1>βt=4.2。综合上述计算结果，对比桥梁结构设计的可靠性指标目标值，表明该连续刚构桥还没有超过使用寿命。

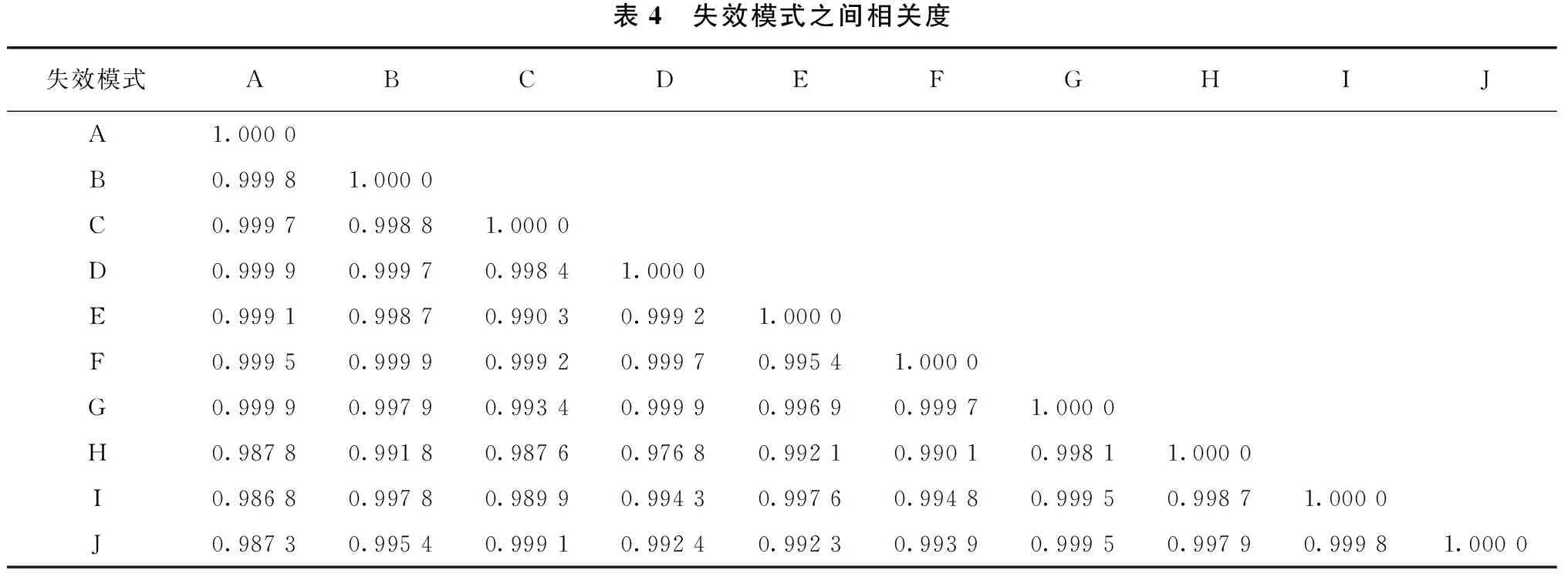
表4 失效模式之间相关度失效模式ABCDEFGHIJA1.0000B0.99981.0000C0.99970.99881.0000D0.99990.99970.99841.0000E0.99910.99870.99030.99921.0000F0.99950.99990.99920.99970.99541.0000G0.99990.99790.99340.99990.99690.99971.0000H0.98780.99180.98760.97680.99210.99010.99811.0000I0.98680.99780.98990.99430.99760.99480.99950.99871.0000J0.98730.99540.99910.99240.99230.99390.99950.99790.99981.0000

4　结论

1) 依据本文所提出的连续刚构桥体系可靠度指标的计算流程得到的可靠指标，能够综合正确地描述连续钢构桥体系失效现象。

2) 运用全局分枝-约界法来找到连续刚构桥的主要失效模式，研究各结构构件的失效形式和失效顺序，研究发现有限元单元的离散程度决定了失效模式对应桥梁失效截面位置的精确程度。

3) 计算得到的各失效模式之间的相关系数基本接近1，说明各个失效模式之间的相关度很高。

4) 由于单个构件的可靠指标要比体系失效可靠指标值大，因此，通过单个可靠指标进行桥梁设计不安全；桥墩失效可靠度指标比主梁大，说明主梁更为容易失效。

[1]沈逢俊.连续刚构桥结构体系可靠度分析[D].西安：长安大学，2007.

[2]高峰.混凝土简支桥梁的体系延性与可靠度研究[J].公路交通技术，2013(4)：66-71.

[3]张业平.连续梁桥结构体系的可靠度研究[D].合肥：合肥工业大学，2004.

[4]秦权，林道锦，梅刚.结构可靠度随机有限元理论及工程应用[M].北京：清华大学出版社，2006.

[5]赵国藩.工程结构可靠性原理与应用[M].大连：大连理工大学出版社，1996.

[6]刘扬，鲁乃唯.钢管混凝土组合高墩连续刚构桥体系可靠指标计算方法[J].公路交通科技，2011(9)：89-95.

[7]袁新鹏.公路预应力混凝土桥梁的可靠度分析[D].成都：西南交通大学，2009.

[8]章劲松.基于可靠度的公路桥梁结构极限状态设计计算原则及应用[D].合肥：合肥工业大学，2007.

[9]董聪，杨庆雄.冗余桁架结构系统可靠性分析理论与算法[J].计算结构力学及其应用，1992，9(4)：393-397.

[10]陈卫东，张铁军，刘源春.高效识别结构主要失效模式的方法[J].哈尔滨工程大学学报，2005，26(2)：202-204.

[11]桂劲松，康海贵.结构分析的响应面法及其MATLAB实现[J].计算力学学报，2004，21(6)：683-687.

[12]张杨永，蔡敏.基于响应面重构的一种可靠度计算方法[J].合肥工业大学学报(自然科学版)，2006，29(4)：482-485.

[13]田浩，陈艾荣.寿命期内预应力混凝土连续梁体系可靠分析[J].哈尔滨工业大学学报，2011，43(10)：105-112.

[14]何嘉年，滕海文，霍达.基于改进PNET法的框架结构体系可靠度计算方法[J].北京工业大学学报，2012，38(5)：708-712.

2015-11-26

彭子茂(1982-)，男，工程师，主要从事公路与桥梁施工技术方面工作。

；1008-844X(2016)03-0159-05

；U 441

；A