大跨度钢桁架拱桥抖振数值仿真分析

张贤文

(湖南省益阳市交通规划勘测设计院，湖南 益阳　413000)



大跨度钢桁架拱桥抖振数值仿真分析

张贤文

(湖南省益阳市交通规划勘测设计院，湖南 益阳413000)

讨论广州南沙区某钢桁拱桥在自然脉动风中的抖振响应，以具体的工程实例，建立有限元模型，基于谐波合成法数值仿真该地区的三维脉动风场，并将风荷载时程作用在该桥的有限元模型中，以此来分析桥梁的抖振效应，得到了由于抖振产生的位移和内力，最后完成对该桥的抖振时域研究。结果表明，模拟出来的三维脉动风场具有较高的准确度，该桥的抖振响应在成桥状态下不会产生风致病害。

；钢桁架拱桥；有限元模型；三维脉动风场；抖振；抖振时域

0　引言

桥梁抖振[1]在桥梁风工程中主要是由于大气的脉动风引起的，在桥梁的风致振动中是最常见的一种振动形式，是紊流风场作用下随机强迫振动，是研究桥梁风致振动的重要内容之一。抖振不仅能引起结构构件的疲劳问题，而且影响大桥行车舒适性，同时还会引起生命财产安全，所以得到了由于抖振产生的位移和内力，完成对该桥的抖振时域研究是十分必要。相比频域法而言，时域法由于可以考虑几何非线性，气动力非线性等影响因素，利用时域法[2]来分析风致振动产生的效应成为研究的主流方向。为此，本文按文献[3]模拟了三维脉动风场对该桥进行抖振时域分析。

1　三维脉动风场模拟

利用数理统计法[4]分析脉动风的一些性质。在桥梁风工程中，通常是把现实中原本三维相关的风速场通过数理统计的方法简化成为x，y，z方向独立的3个一维风速场。

同时依据目标功率谱函数[5]，在进行抖振响应的时域分析中，采用精度高的谐波合成法来人工模拟出空间脉动风场。模拟过程如下所示：

一个一维n变量零均值平稳随机过程，互相关函数矩阵如下式：

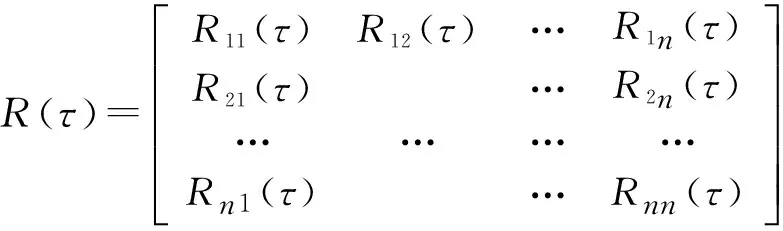
R(τ)=R11(τ)R12(τ)…R1n(τ)R21(τ)…R2n(τ)…………Rn1(τ)…Rnn(τ)éëêêêêêùûúúúúú

其互功率谱密度矩阵为：

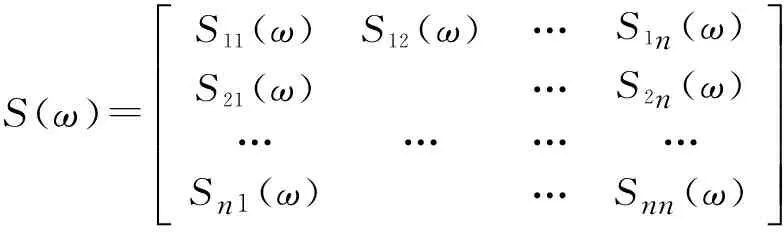
S(ω)=S11(ω)S12(ω)…S1n(ω)S21(ω)…S2n(ω)…………Sn1(ω)…Snn(ω)éëêêêêêùûúúúúú

由平稳随机过程的性质可知：

Rjj(τ)=Rjj(-τ)，j=1，2，…，n

Rmj(τ)=Rjm(-τ)，j=1，2，…，n，m=1，2，…，n，j≠m由维纳-辛钦关系得：

假设n变量模拟出来的随机过程fj(t)，功率谱密度矩阵分解为：

S0(ω)=H(ω)HT*(ω)

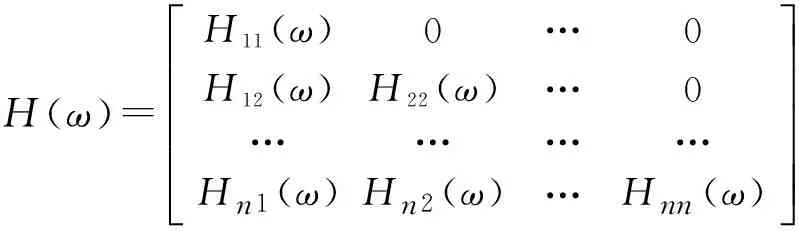
H(ω)=H11(ω)0…0H12(ω)H22(ω)…0…………Hn1(ω)Hn2(ω)…Hnn(ω)éëêêêêêùûúúúúú

式中：

Hjj(ω)=Hjj(-ω)，j=1，2，…，n

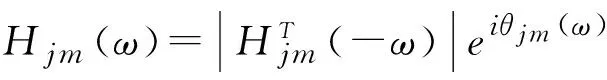
j=1，2，…，n，m=1，2，…，j-1；

式中，j=1，2，…，n，n为模拟点数；N为频率等分数，一般取为2的整数次幂；Δω为频率增量；ωup为截止频率，ωup可用下式估算：

其中，ε<<1，可取ε=0.001；φl为均匀分布在[0，2π)区间的随机相位角；ωl为频率，其表达式有多种，分别为下列各式：

ωl=(l-1/2)Δω，

ωl=lΔω，l=1，2，…，N

其中，δωl为均匀分布在(-Δω′/2，Δω′/2)的随机频率，其中Δω′<<Δω。Shinozuka和Deodatis建议ωml采用双索引频率解决了ωup不可能太小的问题，计算公式如下：

ωml=(l-1)Δω+m/n·Δω，

l=1，2，…，N，m=1，2，…，n

则可以表示为：

2　风场模拟的工程算例

该桥设置为3跨双层钢桁架拱桥，主跨的跨径：436 m，矢跨比：1/5.83。其中，主桁架是由3片桁架拱构成，每片桁架的间距达到了18 m，主跨拱圈矢高：75 m。按照4个独立的一维多变量随机脉动风场来模拟脉动风场[6]，如表1所示。模拟点如图1所示。1～21个模拟点是每隔36 m布置1个；22～36号模拟点也是每隔36 m布置1个，以此来布置拱肋。其中1号点为主梁边上关键点，11号点为主梁跨中关键点，22号点为边拱肋关键点，29号点为拱肋跨中关键点。

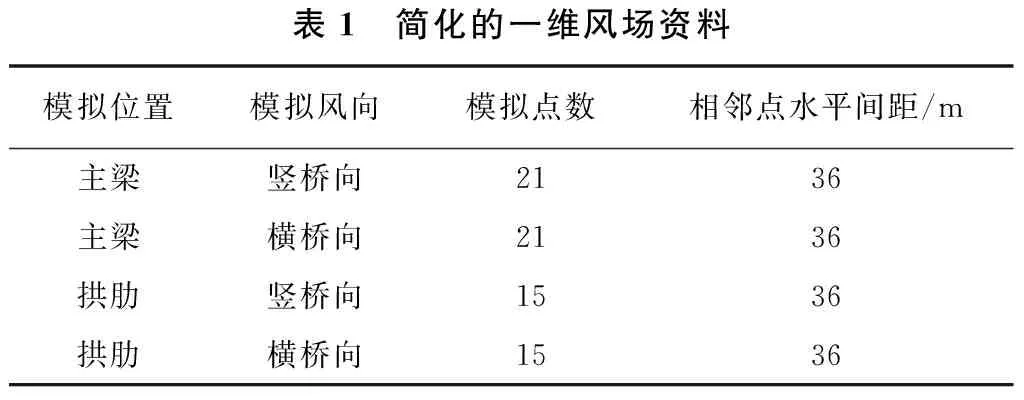
表1 简化的一维风场资料模拟位置模拟风向模拟点数相邻点水平间距/m主梁竖桥向2136主梁横桥向2136拱肋竖桥向1536拱肋横桥向1536

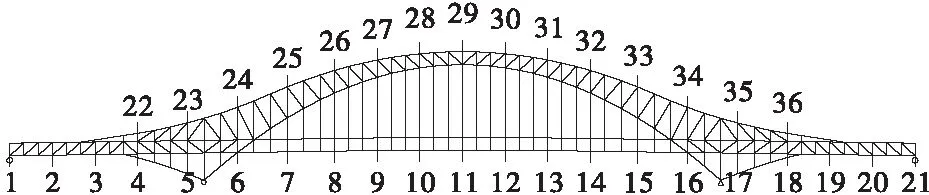
图1　风场模拟点图(单位；m)

由设计资料可知，主桥地面标高为7.3 m，桥面标高50.047 m，桥面处的地貌类别为B类，相应风剖面指数为0.16。因此，对应的主梁设计基准风速为：

按照《公路桥梁抗风设计规范》：

风速相关系数采用Davenport函数形式：

通过以上部分的详述具体参数取值如表2。

应用MATLAB程序，按文献[7]模拟了主梁上1～21号点的横桥向和竖桥向脉动风场。拱肋和主梁跨中节点横桥向模拟的脉动风速时程如图2和图3所示。

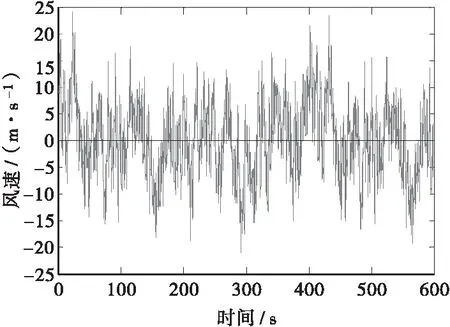
图2　拱肋横桥向跨中风速时程

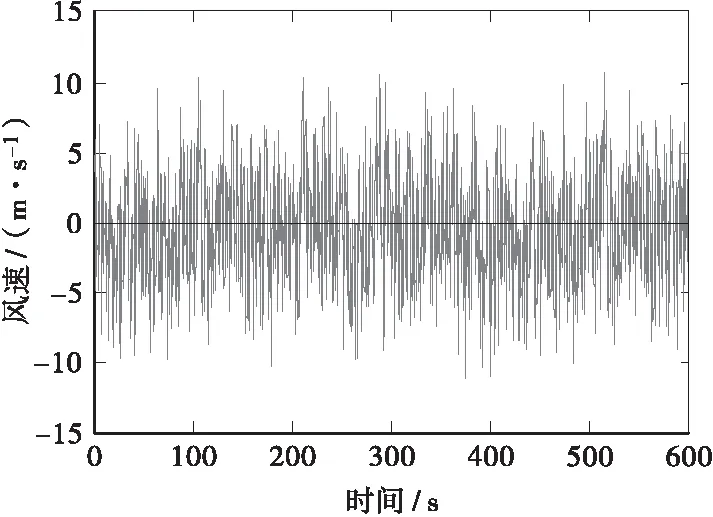
图3　主梁横桥向跨中风速时程

3　桥梁抖振的时域分析

3.1抖振力荷载处理

本文中不考虑气动导纳[8]对全桥抖振响应影响，即将气动导纳取为常数1，作用在单位长度上的抖振力荷载可以根据Scanlan准定常气动力模型理论研究分析，其具体表达式为：

本文只考虑零度风攻角的情况。加载方式采用：

1) 将抖振力时程直接加载在主梁和拱肋的节点上，同时考虑D、L和M的作用。

2) 吊索的抖振力只分析D的影响，参数取值与静风响应分析相同。

3) 迎风面桁架和背风面桁架的风荷载分配仍然遵循静风响应分析的遮挡系数进行取值。

抖振力时程直接作用在有限元模型的节点上，运用瞬态分析中的模态叠加法进行分析，时间步长风荷载模拟中的时间步长一致，总时长600 s，结构阻尼采用规范规定来进行选择。主梁跨中11号点处抖振力时程见图4，拱顶处29号点的抖振力时程见图5。

图4　跨中11号点处抖振阻力时程

图5　拱顶29号点处抖振阻力时程

3.2抖振响应分析

成桥状态的抖振响应分为抖振力和抖振位移两个方面，杆件抖振力太大则容易引起结构的疲劳破坏，节点抖振位移[9]也是评价安全与否的重要指标。为了简化计算，通常只考虑了拱肋的阻力，而忽略了升力和扭矩的作用。本文基于拱肋三分力试验的基础上，可以直接测出拱肋的三分力系数，故加载考虑了拱肋的阻力、升力和扭矩。应用ANSYS15.0研究该桥，计算结果如表3，其中RMS值表示响应的均方根值。

通过对表3数据的分析，成桥状态竖向的位移峰值在桥面跨中位置处，最大值达到2.025 cm，横桥向的位移最大值则是在桥梁的拱肋跨中出现，达到14.78 cm；各个关键扭转位移均很小，基本可以忽略不计，说明该桥发生扭转失稳的可能性很小。主梁1/4跨正好位于拱梁结合处，此处刚度很大，故抖振位移比较小，边跨由于支座的存在，从而限制各向位移了，抖振位移也很小。主梁和拱肋侧向位移RMS值沿桥跨向的变化曲线如图6所示，竖向位移RMS值沿桥跨向的变化曲线如图7所示。成桥状态拱肋中跨位置处横桥向和竖向位移时程曲线如图8和图9所示。表4为成桥状态控制杆件的抖振内力的峰值和均方根值。

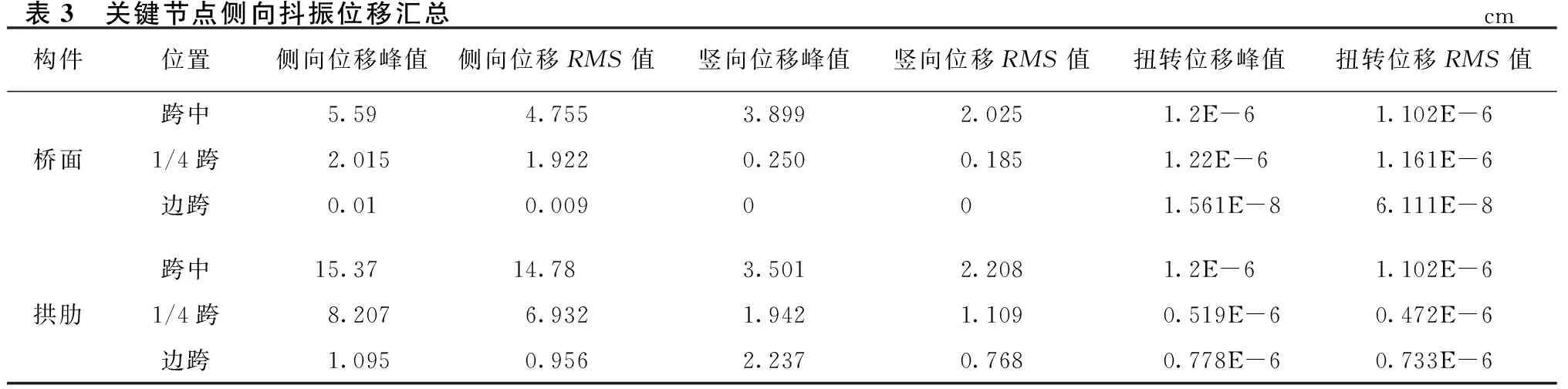
表3 关键节点侧向抖振位移汇总cm构件位置侧向位移峰值侧向位移RMS值竖向位移峰值竖向位移RMS值扭转位移峰值扭转位移RMS值桥面跨中5.594.7553.8992.0251.2E-61.102E-61/4跨2.0151.9220.2500.1851.22E-61.161E-6边跨0.010.009001.561E-86.111E-8拱肋跨中15.37 14.78 3.5012.2081.2E-61.102E-61/4跨8.2076.9321.9421.1090.519E-60.472E-6边跨1.0950.9562.2370.7680.778E-60.733E-6

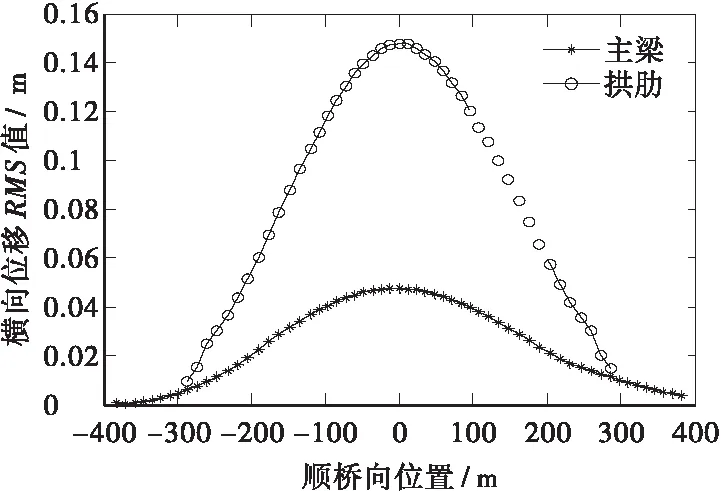
图6　主梁和拱肋侧向位移RMS值

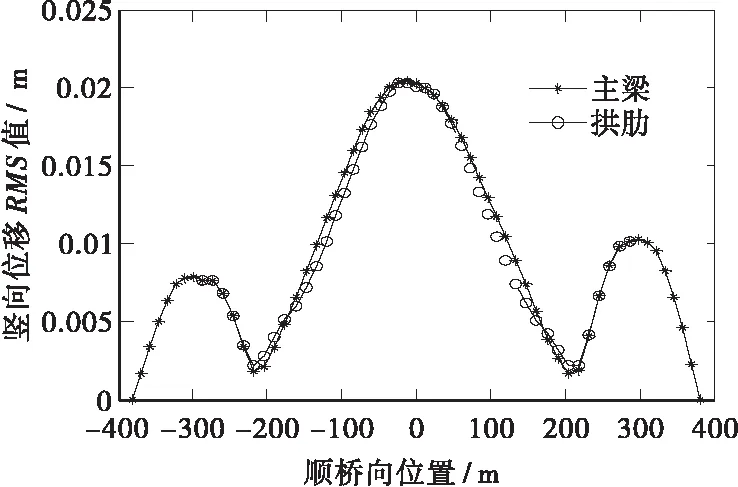
图7　竖向位移RMS值

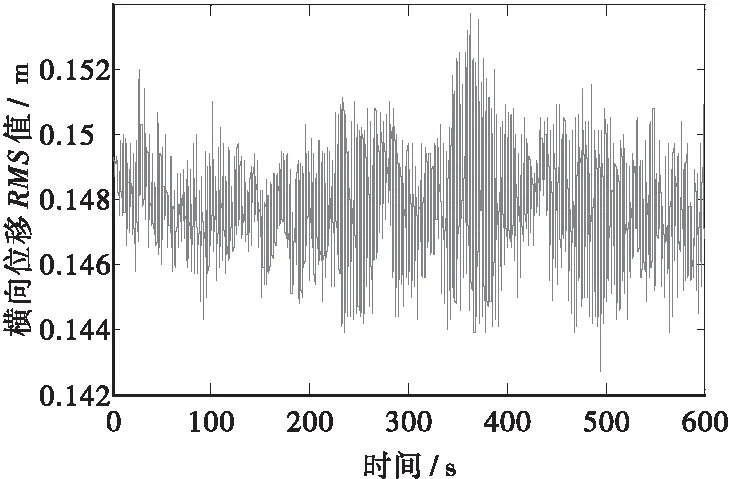
图8　拱肋中跨横桥向时程曲线

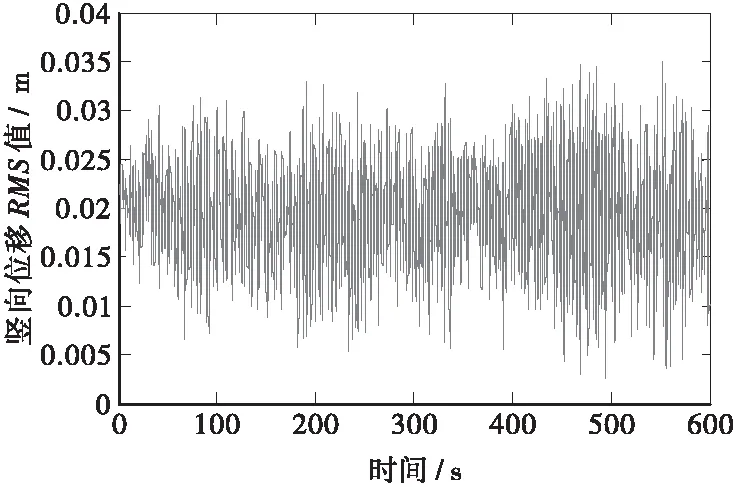
图9　拱肋中跨竖向位移时程曲线

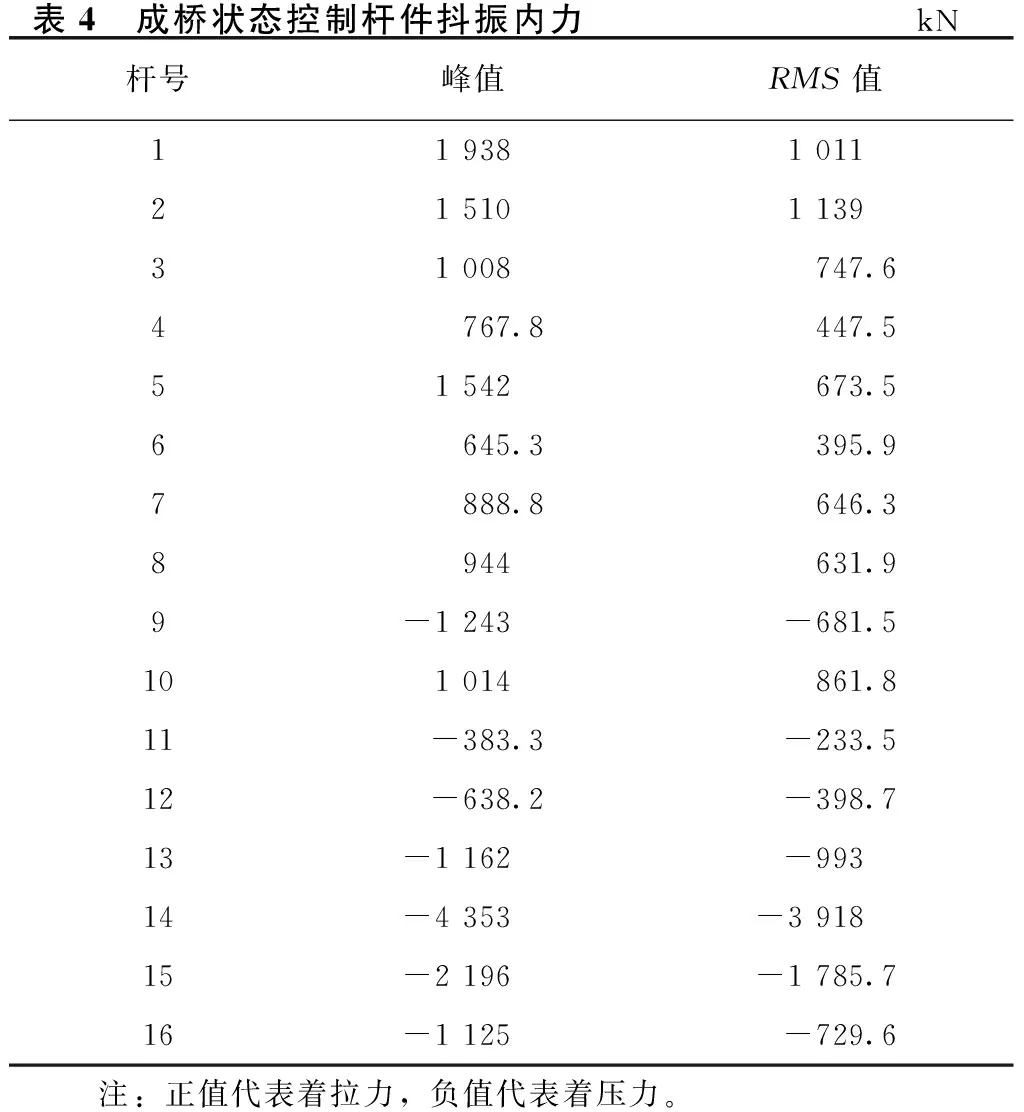
表4 成桥状态控制杆件抖振内力kN杆号峰值RMS值11938101121510113931008747.64767.8447.551542673.56645.3395.97888.8646.38944631.99-1243-681.5101014861.811-383.3-233.512-638.2-398.713-1162-99314-4353-391815-2196-1785.716-1125-729.6 注:正值代表着拉力,负值代表着压力。

4　结论

本文主要讨论了广州南沙区某钢桁拱桥在自然脉动风中的抖振响应。开始分析了该桥所处区域的

风环境，选取规范建议的风谱，通过谐波合成法模拟了该地区的三维脉动风场。其次，通过对模拟的风场数值模拟分析得到了一系列可靠的结果。最后完成了对该桥的抖振分析，取得的主要计算分析成果如下：

1) 设计了成桥状态的有限元模型，计算并分析了全桥在该成桥状况下的内力与位移变化值。

2) 本桥在成桥状态下在跨中位置位移达到了最大值，其中，桥面主梁达到了竖向位移的最大值，拱顶的位置达到横向位移的最大值，可见桥面的竖弯刚度较低，而拱肋的侧弯刚度较低，切合横向宽度较大公路钢桁架拱桥[10]的特点。

[1]吉孔东.结构阻尼对桥梁风振的影响及复合阻尼比的计算[D].西安：长安大学，2010.

[2]徐洪涛.山区峡谷风特性参数及大跨度桁梁桥风致振动研究[D].成都：西南交通大学，2009.

[3]陈艳伟.大跨悬索桥非平稳抖振位移响应时域分析[D].哈尔滨：哈尔滨工业大学，2014.

[4]李韬.双烟囱相互干扰下风振特性试验研究[D].成都：西南交通大学，2015.

[5]任银飞.大跨度斜拉桥风致振动响应分析研究[D].合肥：合肥工业大学，2009.

[6]曾满良.大跨度分路钢桁拱桥风致抖振时域分析[D].成都：西南交通大学，2011.

[7]孙刘军.大跨度连续钢桁梁拱桥时域抖振分析[D].成都：西南交通大学，2009.

[8]韩艳.桥梁结构复气动导纳函数与抖振精细化研究[D].长沙：湖南大学，2007.

[9]胡峰强，陈艾荣，林铁良.杭州湾南航道独塔斜拉桥抗风性能试验研究[J].工程力学，2006，23(8)：132-137.

[10]李红征.贵广铁路大跨度钢桁架拱铁路桥施工技术研究[D].成都：西南交通大学，2013.

2016-07-27

张贤文(1977-)，男，高级工程师，主要从事道路桥梁设计工作。

；1008-844X(2016)03-0098-04

；U 448.22+4

；A