一种并网逆变器的电容电流单周期控制技术

吴　静，刘晓东，方　炜，刘宿城

（安徽工业大学电力电子与运动控制重点实验室，马鞍山243002）

一种并网逆变器的电容电流单周期控制技术

吴静，刘晓东，方炜，刘宿城

（安徽工业大学电力电子与运动控制重点实验室，马鞍山243002）

在LCL型并网逆变器传统双环结构（电容电流内环、并网电流外环）基础上，提出一种结合数字单周期控制和准比例谐振控制的新型电流控制策略。在αβ静止坐标系下，将单周期控制应用于系统内环，推导出了电容电流单周期数字控制占空比函数，提高了系统抗干扰能力并简化调节过程；外环采用准比例谐振控制器直接控制并网电流，省去了复杂的坐标变换，计算简单。最后，实验结果表明所提出控制策略能够实现逆变器有效并网，且动态性能良好。

并网逆变器；准谐振控制器；单周期控制；LCL滤波器；电容电流反馈

引言

三相电压型全桥式并网逆变电路结构简单可靠、直流电压波动较小，电路所用元器件较少，在并网逆变领域应用广泛［1-3］。为了确保逆变器输出并网电流的波形质量满足各种标准要求，其输出交流侧滤波环节通常采用LCL滤波器来抑制并网电流的谐波含量。与L型滤波器相比，LCL滤波器呈三阶传递特性，滤波效果好于L型滤波器［4-6］，可以以较小的体积和损耗滤除逆变电路输出电流的高次谐波及高频纹波。但是LCL滤波器存在高频谐振问题，谐振频率处产生的谐振峰导致了系统谐波含量超标甚至影响系统稳定性，因此需要增加系统阻尼予以抑制谐振发生。

目前解决谐振问题的策略主要有无源阻尼法和有源阻尼法［7］。无源阻尼法实现简单，不受开关频率限制，其基本思想是在硬件电路系统中添加电阻元件，增加系统阻尼，从而达到抑制谐振的效果，如在LCL滤波器电容支路串并接阻尼电阻［8］等。但阻尼电阻的加入不仅消耗系统有功功率，增加系统损耗，也抑制了滤波器的高频衰减能力，降低滤波性能。而有源阻尼法则是通过选择额外的状态反馈量构建一定的控制结构并通过控制算法实现系统虚拟阻尼的增加，抑制谐振发生［9］，避免了功率损耗和热消耗。诸如电容电流比例反馈法［10-11］，逆变器侧电感电流反馈法［12］，滤波电容电压微分反馈法［13］和基于超前-滞后网络的桥臂电流有源阻尼复合反馈法［14］等多种有源阻尼策略虽然抑制了谐振峰发生，增加了系统稳定性，但是额外引入状态变量反馈需要较多的电压/电流传感器，增加了系统成本和硬件电路复杂度。而系统基于有源阻尼策略构建的多环多变量控制系统更是增加了控制系统设计的难度与复杂度，也使得控制器参数对环境参数的影响更为敏感，降低了系统的抗干扰能力。

在此基础上，本文提出了电容电流内环的数字单周期控制律，简化了控制器有源阻尼内环设计过程，使系统具有优良的抗干扰能力。外环则是采用αβ静止坐标系下准比例谐振控制器［15-16］实现对并网电流的直接控制。最后，以TMS320F28335DSP为数字控制核心研制了一台1.5 kW的实验样机，验证了所提出控制方案的合理性和可行性。

1　电容电流单周期控制原理

1.1电容电流单周期原理推导

本文选取三相LCL型并网逆变器作为系统主电路，电路拓扑如图1所示。其中，ua、ub、uc为三相电网相电压，L1为逆变器侧的电感，L2为电网侧的电感；i1为逆变器侧电感的各相电流，i2而为电网侧电感的各相电流；Cf为滤波电容，ic为滤波电容电流；S1-S6为IGBT功率器件，Udc为直流侧电压，Cdc为直流侧滤波电容。

图1　三相并网逆变器主电路Fig.1　Three-phase inverter with LCL filter

单周期控制技术是Keyue M.Smedley提出的一种非线性控制技术，电路结构简单、动态响应快、稳定性好，能有效地抵制电源侧的扰动，消除稳态误差和暂态误差。分析单周期控制过程前，做如下假设：①三相电网电压对称，内阻为0；②开关器件均为理想器件，且每桥臂上、下两开关管互补运行，忽略死区影响；③不考虑系统延迟。

设开关管 S1、S3、S5占空比分别为 dap、dbp和dcp；则S2、S4、S6占空比分别为1-dap、1-dbp和1-dcp。以A相电路为例，电路存在2种开关状态（S1导通S4关断和S1关断S4导通）。则电路正常运行时一个开关周期内VAN、VBN、VCN的平均值满足条件为

由图1可得

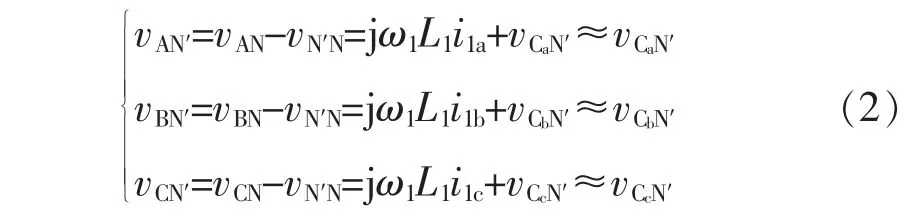
由于三相系统对称，则有：vCaN′+vCbN′+vCcN′=0。结合式（1）～式（2），可得

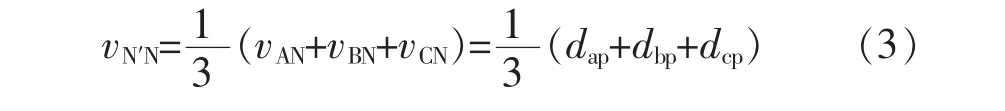
同理可得

由双极性SPWM调制原理可得，三相系统对称时，任意开关周期均有

结合式（3）～式（5），A相开关过程电路等效电路如图2所示。

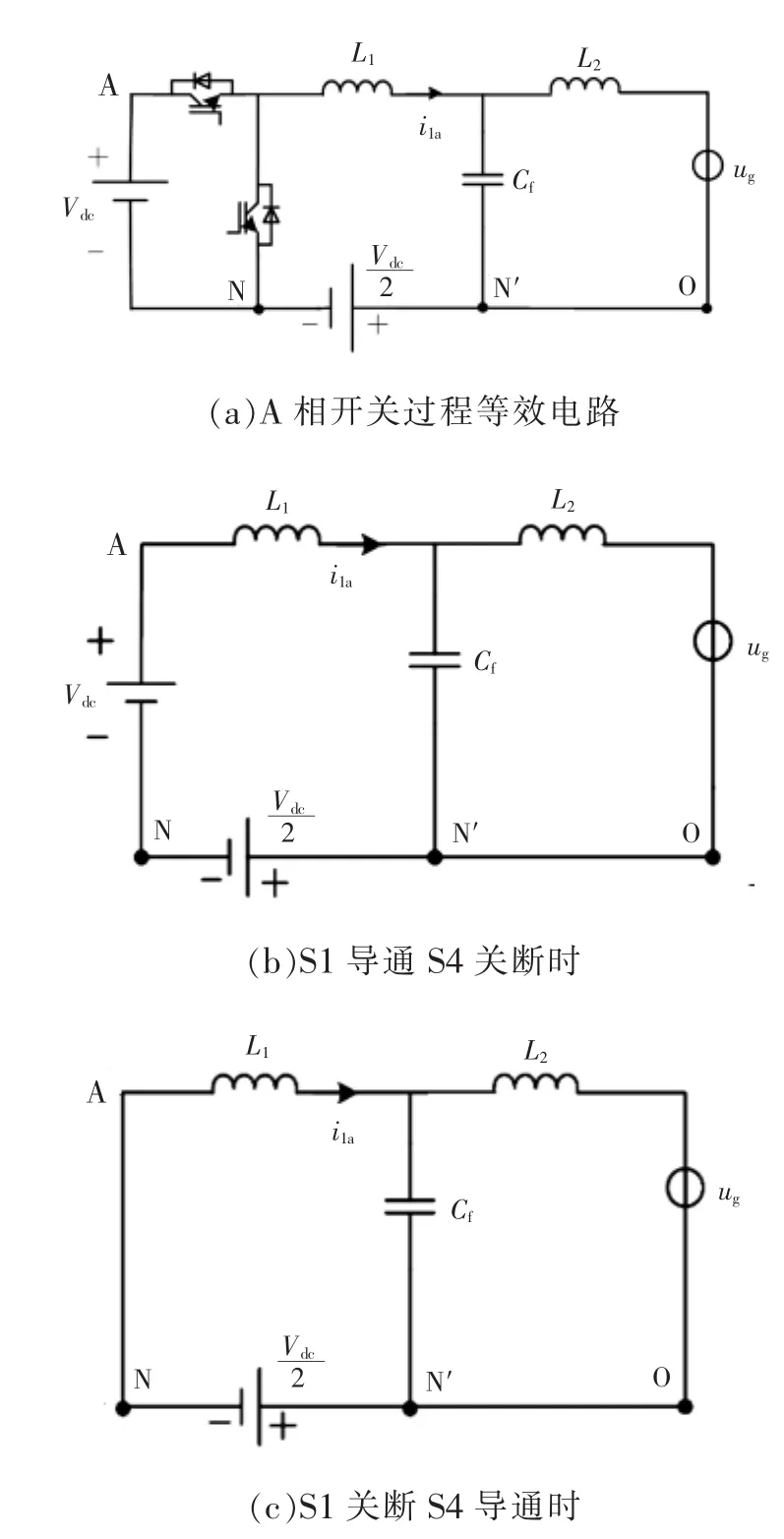
图2　A相开关过程等效电路Fig.2　Equivalent circuit of A-phase in switching process

由图2可知

因开关频率fsw远大于电网基本频率f1，所以在每个开关周期Ts内，电网电压vg视为定值。则电路正常运行时i1a在一个开关周期Ts内的平均值〈i1a〉满足条件为

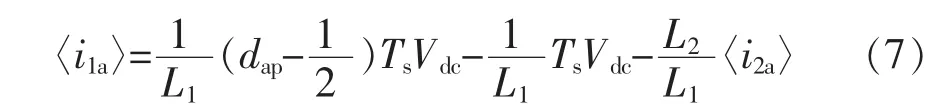
由于电流i2a的幅值跟随电网电压vga呈正弦变化，所以有

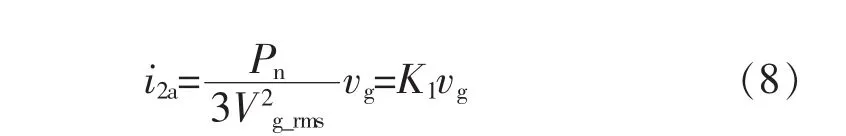
将式（8）代入式（7），则有

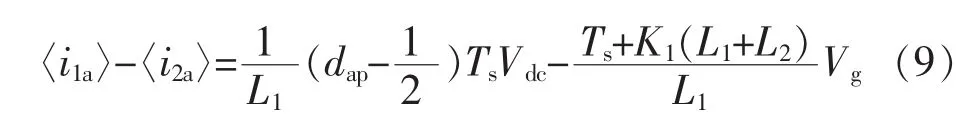
由电感L2的伏秒平衡原理可得

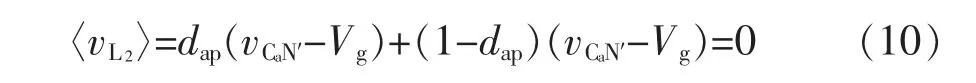
则〈vCaN′〉=Vg。

电容Cf在一个开关周期Ts平均电压满足的条件为

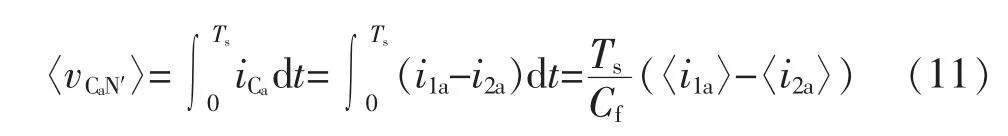
将式（11）～式（12）代入式（9）可得

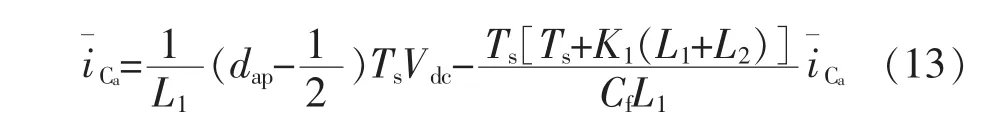
则A相占空比为

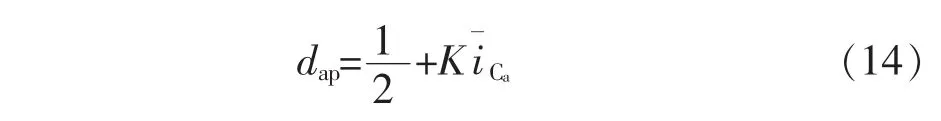
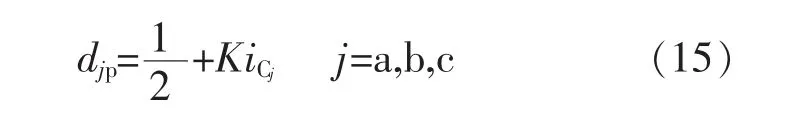
1.2电容电流环的数字实现

由式（15）可知，电容电流的单周期控制率需检测每个开关周期内电感电流i1j和i2j的平均值。式（15）离散化处理后，可得到数字占空比为

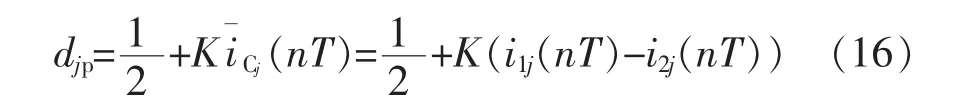
同理可得三相电容电流的数字单周期控制双极性控制率为

以A相并网电流为例，当i2a＞0时，电流i2a变化示意如图3所示。根据图3，电感电流i2a在每个开关周期内的平均值为

同理则有

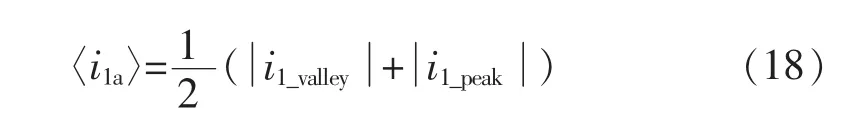
图3　电感L2电流变化示意Fig.3　Schematic of the change with inductor L2current

在TMS320F28335DSP中设置ePWM模块的时基（TB）部分为增减计数，若ePWM模块在定时器计数值为零时启动ePWM中断，则ePWM模块所产生的六路PWM脉冲均为中心对称PWM波形，且对称阵轴相同。如果设置此时启动ADC转换，采样点恰好为一个开关周期内电感电流上升的中间值，可近似认为是电感电流的平均值。且此时处于开关管导通的中点，远离IGBT导通点和关断点，电感电流相对稳定一些，其电流采样示意如图4所示。

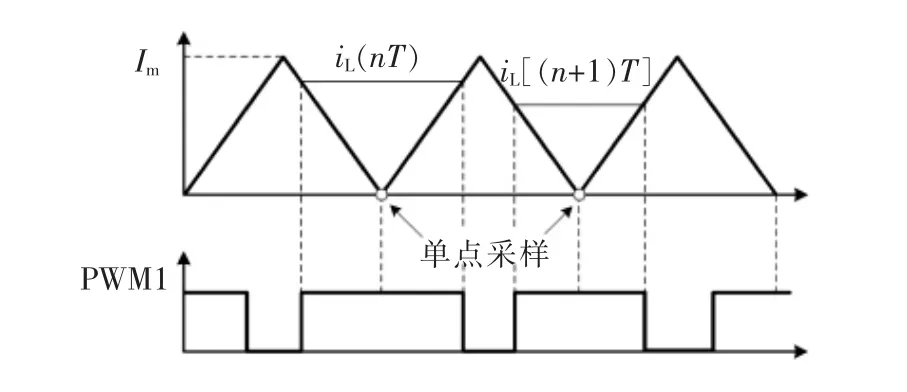
图4　电感电流采样示意Fig.4　Sketch map of sampling of inductor current

2　双环电流控制系统设计

2.1并网电流外环——QPR控制器

比例谐振控制策略算法简单，谐波补偿易实现，具有良好的稳态性能。PR控制可以在静止坐标系下实现对交流量的直接控制，不需要进行复杂的坐标变换，解决了PI控制在跟踪正弦量时存在幅值和相位的稳态误差问题，其传递函数为

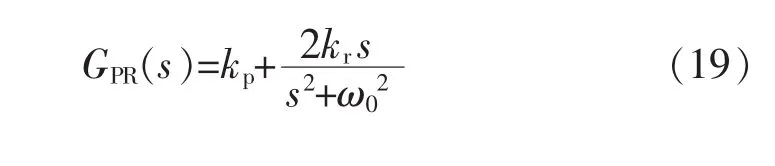
由式（19）可知，PR控制器在基波频率处的增益趋近于无穷大，可实现对正弦基波信号的无静差跟踪。但在实际系统中，理想PR控制器是难以实现的，因其带宽小，若电网频率发生偏移，则不能有效抑制电网谐波。故本文采用一种易实现的准比例谐振QPR（quasi proportional resonant）控制器。QPR控制器在谐振点附近一定带宽的频率范围内，仍可以维持较高的增益，解决了实际谐振频率与设计谐振频率略有偏差时增益大幅下降的问题，其传递函数为

式中：kp为比例系数；kr为谐振系数；ωc为截止频率；ω0为电网基波角频率，ω0=314 rad/s。ωc是QPR控制器的带宽。经计算，QPR控制器的带宽满足BW= ωc/π。一般来说ωc取3～6 rad/s，这里取ωc=5 rad/s。

由于QPR控制器由比例环节与广义积分器并联组成，广义积分器主要用于保证控制系统对基波电流指令的无静差跟踪（kr和ωc决定了控制器所需增益和带宽），比例环节承担大部分的电流稳态跟踪和动态响应任务：随着kp的增大，系统谐波阻抗增大，系统的抗扰性能越好；但是kp过大时控制器频带变宽，选频特性变差；且系统的主导极点靠近虚轴，大大降低系统的稳定裕度，使系统稳定性变差。因此，在设计QPR控制器时通常需综合考虑系统的稳定性和抗扰性能，而本文在电容电流内环引入了抗扰性能优良的单周期控制律，减少了QPR控制器对比例环节的依赖性，可以更好地发挥其无静差跟踪正弦信号的能力。

2.2逆变控制系统原理

由LCL型三相全桥式并网逆变器dq坐标系下状态方程可知，d轴与q轴之间存在的强耦合关系，使d轴与q轴的状态变量相互影响，不能独立控制，需进行解耦运算以获得理想的跟踪性能。但是解耦算法引入过多状态量，使控制系统设计过程变得更为复杂，降低了控制系统鲁棒性。而在两相静止坐标系（αβ系）下，α轴和β轴不存在任何耦合关系，三相全桥式逆变电路可以等效为2个单相逆变器。无需解耦运算，实现也较为容易。由abc坐标系至αβ坐标系的转换矩阵Tabc→αβ为

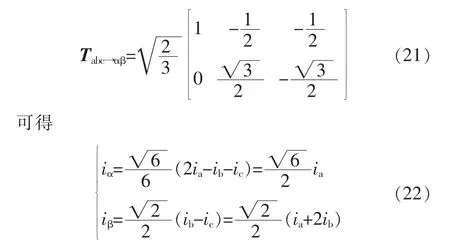
因此，三相系统对称运行时，只需采样A相和B相各控制量，即可完成控制系统的构建，一定程度上减少电压/电流传感器的数量，降低硬件成本。

在此基础上，本文结合有源阻尼策略和准比例谐振控制策略，以α轴和β轴上的并网电流和电容电流为被控量，构建双环控制结构，控制策略原理及控制系统框图如图5所示。以并网电流反馈构建的外环采用QPR控制器，利用其跟踪基波正弦信号无静差的特点，实现进网电流的零稳态误差，保证高的进网电流功率因数。以电容电流为有源阻尼反馈量构成内环，增加了系统有效阻尼，抑制谐振发生；同时由于内环采用基于单周期数字控制，能够有效抵御电源侧输入扰动，加快了系统的动态响应速度，提升了系统动态性能和抗扰能力，弥补了QPR控制动态特性差的缺点。特别是在电网电压发生频率偏离，QPR控制器因增益下降而危害系统稳定性时，单周期控制器能够使系统稳定性得到保障。此外，采用PLL锁相环，实现了并网电流与电网电压的同频同相。

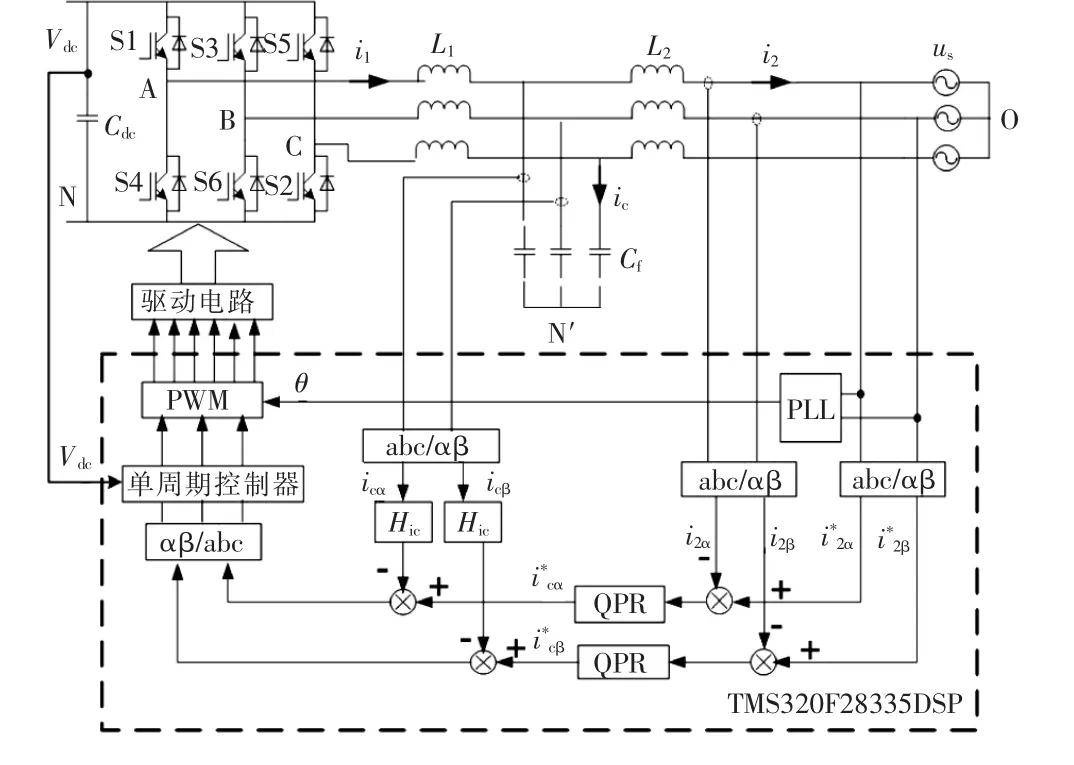
图5　并网逆变器控制系统框图Fig.5 Control system black diagram of three-phase grid-connected inverter with LCL filter

3　实验研究

为验证本文所提出算法和控制策略的正确性，搭建了基于TMS320F28335DSP的实验样机，通过数字控制电路调试得出了相关主要实验结果，实验波形如图6、图7所示。并网逆变样机技术指标为：Vdc=200 V，逆变器输出相电压峰值Vpahse_peak=100 V，输出有功功率1.5 kW，开关频率10 kHz，以验证所提出控制策略的可行性。

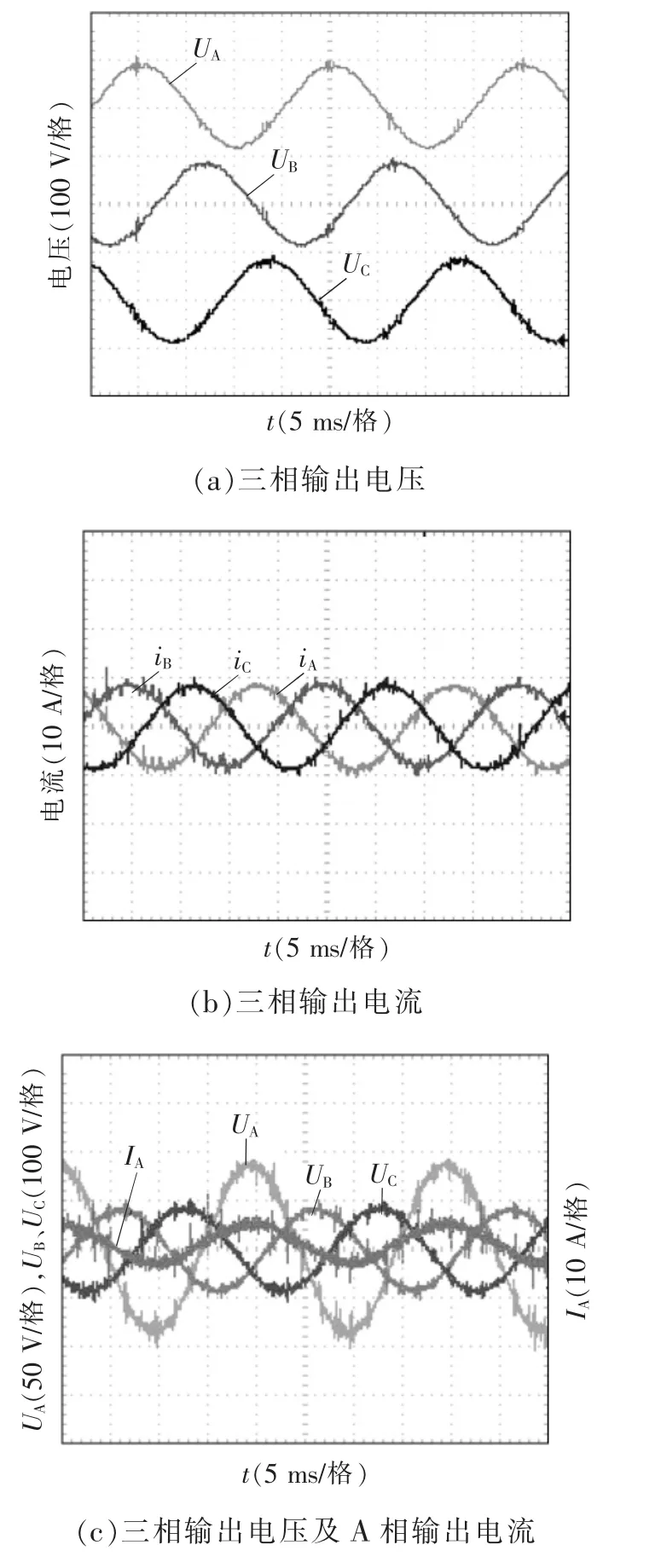
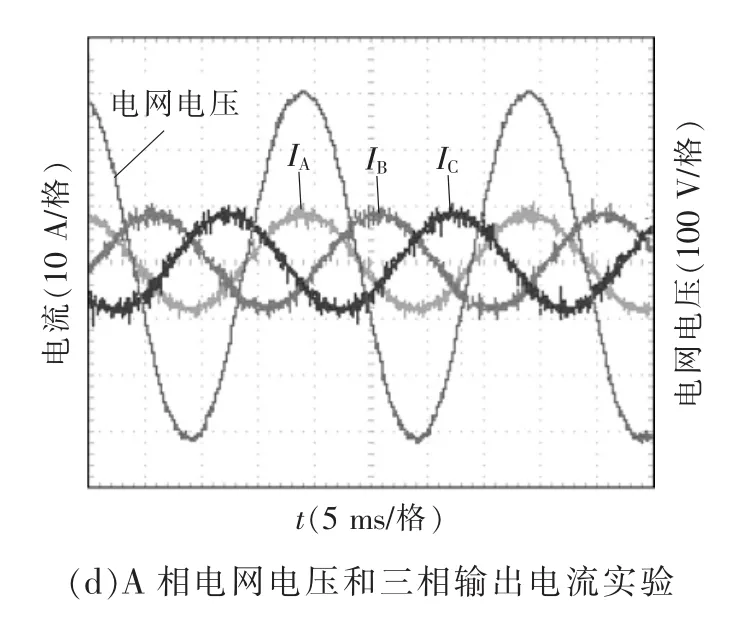
图6　稳态时三相并网电流及电压波形Fig.6　Oscillograph of three-phase currents and voltages in steady operation

系统稳态运行时，输出三相电压及其电流波形如图6（a）～（b）所示。由图6（a）～（b）可看出，并网电流的各次谐波得到很好抑制，开关纹波得到有效衰减，系统处于稳定运行状态。三相输出电流与A相电网电压的波形如图6（c）所示，图6（d）为A相电网电压和三相并网电流实验波形。从图6（a）～（c）中可以看出，逆变器输出的各相电压和各相电流波形均接近于正弦波形，频率均为50 Hz，且输出电压及其电流满足同相位关系。由图6（d）可以看出：逆变器入网电流能准确跟踪电网电压波形，锁相环工作正常，证明了控制策略的可行性。

图7为负载跳变时并网电流实验波形，图（a）为负载发生正跃变（5 A→10 A）、图（b）为负跃变（10 A→5 A）时入网电流波形，此时直流输入电压始终为Vdc=200 V。由图7可以看出，负载发生跳变时，逆变器输出并网电流波动较小，能够实现平稳过渡，输出电流在2～3个电网周期后就能达到新的稳态。

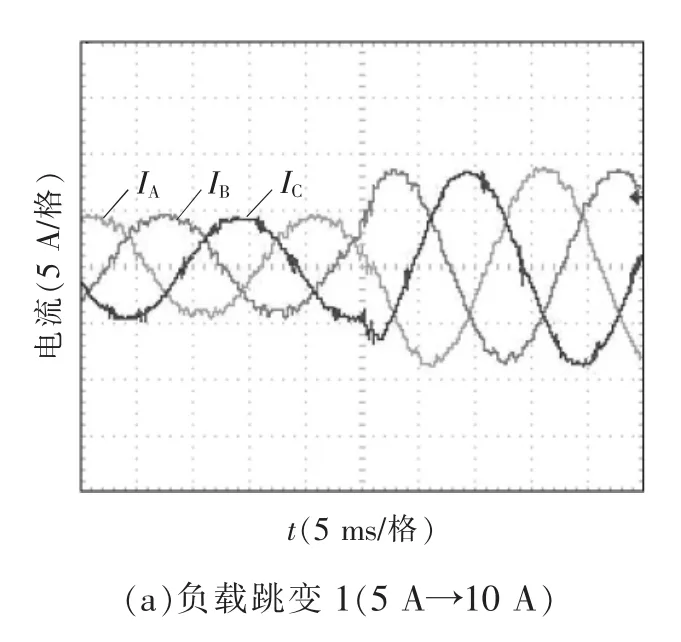
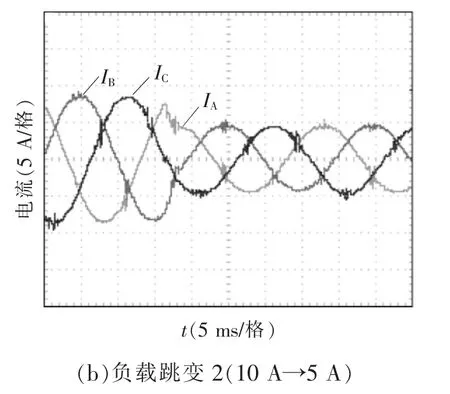
图7　负载跳变实验波形Fig.7　Experimental waveforms of load step changing

4　结语

本文推导出了应用于电容电流内环的单周期双极性控制律，增加系统有效阻尼，增强控制系统稳定性；得到了αβ坐标系下基于单周期控制和准比例谐振控制的电流双闭环控制策略，实现了对并网电流的直接控制。实验结果表明在该控制律下各相电流能跟随相应电网电压成正弦变化，并且系统有很好的动态响应性能。

［1］魏星，肖岚，姚志垒，等.三相并网逆变器的LCL滤波器设计［J］.电力电子技术，2010，44（11）∶13-15.Wei Xing，Xiao Lan，Yao Zhilei，et al.Design of LCL filter for three-phase grid-connected inverter［J］.Power Electronics，2010，44（11）∶13-15（in Chinese）.

［2］Sastry J，Ojo O，Wu Z.High-performance control of a boost AC-DC PWM rectifier/induction generator system［J］.IEEE Transactions on Industry Applications，2006，42（5）：1146-1154.

［3］Yang Chen，Keyue S.Three-phase boost-type grid-connected inverter［J］.IEEE Transactions on Power Electronics，2008，23（5）∶2301-2309.

［4］Suzan E，Majid P，Alireza B.Composite nonlinear feedback control and stability analysis of a grid-connected voltage source inverter with LCL filter［J］.IEEE Transactions on Industrial Electronics，2013，60（11）∶5059-5074.

［5］郑昕昕，肖岚，王长宝，等.三相变流器LCL滤波器参数优化新方法［J］.中国电机工程学报，2013，33（12）∶55-63.Zheng Xinxin，Xiao Lan，Wang Changbao，et al.A new parameter optimization method of LCL filters in threephase converters［J］.Proceeding of the CSEE，2013，33（12）∶55-63（in Chinese）.

［6］陆晓楠，孙凯，黄立培.微电网中并联LCL滤波器谐振特性［J］.清华大学学报：自然科学版，2012，52（11）∶1571-1576.Lu Xiaonan，Sun Kai，Huang Lipei.Resonance characteristics in a parallel LCL filter system for microgrid applications［J］.J Tsinghua Univ∶Sci&Tech，2012，52（11）∶1571-1576（in Chinese）.

［7］朱瑞林，韩金刚，汤天浩.并网逆变器LCL型滤波器的设计及有源补偿［J］.电源学报，2012，10（3）∶43-47.Zhu Ruilin，Han Jingang，Tang Tianhao.Design and active compensation of LCL filter for grid-connected inverter［J］.Journal of Power Supply，2012，10（3）∶43-47（in Chinese）.

［8］仇志凌，杨恩星，孔洁，等.基于LCL滤波器的并联有源电力滤波器电流闭环控制方法［J］.中国电机工程学报，2009，29（18）∶15-20.Qiu Zhiling，Yang Enxing，Kong Jie，et al.Current loop control approach for LCL-based shunt active power filter ［J］.Proceedings of the CSEE，2009，29（18）∶15-20（in Chinese）.

［9］肖华锋，许津铭，谢少军.LCL型进网滤波器的有源阻尼技术分析与比较［J］.电力自动化设备，2013，33（5）∶55-59.Xiao Huafeng，Xu Jinming，Xie Shaojun.Analysis and comparison of active dampling technologies for LCL filter ［J］.Electric Power Automation Equipment，2013，33（5）∶55-59（in Chinese）.

［10］Dannehl J，Liserre M，Fuchs F.Filter-based active damping of voltage source converters with LCL-filter［J］.IEEE Transactions on Industrial Electronics，2011，58（8）∶3623-3633.

［11］Dannehl J，Fuchs F，Hansen S，et al.Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters with LCL filters［J］.IEEE Transactions on Industry Applications，2010，46（4）∶1509-1517.

［12］胡雪峰，韦徵，陈轶涵，等.LCL滤波并网逆变器的控制策略［J］.中国电机工程学报，2012，32（27）∶142-148.Hu Xuefeng，Wei Zheng，Chen Yihan，et al.A control strategy for grid-connected inverters with LCL filters［J］.Proceedings of the CSEE，2012，32（27）∶142-148（in Chinese）.

［13］Vladimir B，Vikram K.A novel control to actively damp resonance in input LC filter of a three-phase voltage source converter［J］.IEEE Trans on Industry Application，1997，33（2）∶542-550.

［14］杨淑英，张兴，张崇巍，等.LCL滤波电压源并网逆变器多环控制策略设计［J］.电力系统自动化，2011，35（5）∶66-70.Yang Shuying，Zhang Xing，Zhang Chongwei，et al.Strategy design of multiple feedback loop control for grid-connected voltage source inverter with LCL filter［J］.Automation of Electric Power Systems，2011，35（5）∶66-70（in Chinese）.

［15］Liu Bo，Yang Xu，Zhang Yan，et al.A new control strategy combing PI and quasi-PR control under rotate frame for three phase grid-connected photovoltaic inverter［C］.8th International Conference on Power Electronics-ECCE Asia，2011，Jeju，Korea∶882-888.

［16］Shen Guoqiao，Zhu Xuancai，Zhang Jun，et al.A new feedback method for PR current control of LCL-filter-based grid-connected inverter［J］.IEEE Trans on Industrial Electronics，June 2010，57（6）∶2033-2041.

A New One-cycle Control Strategy of Capacitor Current on Grid-connected Inverter

WU Jing，LIU Xiaodong，FANG Wei，LIU Sucheng
（Key Lab of Power Electronics&Motion Control，Anhui University of Technology，Ma’anshan 243002，China）

On the basis of double-loops control structure of capacitive current being inner loop and net current being outer loop，a new current control strategy is proposed combining one-cycle digital control strategy with QPR controller.One-cycle controller is applied in the system inner loop in αβ stationary reference frame，and then，the duty function of one-cycle control bipolar algorithm of capacitor current is obtained to improve the anti-jamming performance of the system and to simplify the tuning process.The quasi proportional resonant（QPR）controller of the outer loop is adopted to control the grid-connected currents directly without complicated coordinates transform.Finally，Experimental results indicate that the proposed control scheme allows three-phase gird-tied inverter to meet the grid-connected demands，and the system has a good dynamic performance.

grid-connected inverter；quasi proportional resonant（QPR）controller；one-cycle-control；LCL filter；capacitor current feedback

吴静

10.13234/j.issn.2095-2805.2016.3.62

TM46

A

吴静（1988-），女，硕士研究生，研究方向：电力电子功率变换技术方面研究，E-mail：qishu_1543@126.com。

刘晓东（1971-），男，通信作者，博士，教授，研究方向：电力电子功率变换技术方面研究，E-mail：lxdong168@sina.com。

方炜（1977-），男，博士，副教授，研究方向：电力电子功率变换技术及非线性控制方面研究，E-mail：fwei2k@hotmail.com。

刘宿城（1981-），男，博士，讲师，研究方向：电力电子系统的大信号分析与控制，分布式电源系统的建模与分析以及高性能功率放大技术，E-mail：liusucheng@ahut.ed u.cn。

2015-08-19

国家自然科学基金资助项目（51207001）；安徽省自然科学基金资助项目（1308085ME66）。

Project Supported by the National Science Foundation of China （51207001）；Anhui Provincial Natural Science Foundation（13 08085ME66）