带有随机激活机制的钝化网络模型研究

王学文,罗月娥,潘伟伟,杨　丰

(1.贵州师范学院物理与电子科学学院，贵州贵阳　550018;2.景德镇陶瓷学院机械电子工程学院，江西景德镇　333403)



带有随机激活机制的钝化网络模型研究

王学文1,罗月娥1,潘伟伟1,杨丰2

(1.贵州师范学院物理与电子科学学院，贵州贵阳550018;2.景德镇陶瓷学院机械电子工程学院，江西景德镇333403)

在一般的钝化网络模型中，节点从活性态到钝化态的变化是一个绝对钝化过程，即不可逆的老化过程.在实际情况中，已经失去活性的节点在某一情况下又会被重新激活，成为活性态节点.本文提出了带有随机激活行为的钝化网络模型,采用差分方程和率方程分别对网络演化过程中的活性态节点和休眠态节点进行了描述，对网络中的度分布进行解析求解和数值模拟，得到了相一致的结果.

钝化网络；钝化；激活；度分布；

复杂网络是研究复杂系统的有力工具.如果网络中用节点来代表个体，用节点之间的连边来表示个体间的相互作用，真实系统就能够抽象成网络来进行研究[1-2].自从BA模型提出以来，有关增长网络模型的性质和动力学得到了深入研究[3-6].然而在真实的网络世界中，节点的老化效应也非常重要，由此人们对于老化网络也进行了深入研究[7-11].Dorogovtsev等[7]在BA模型的基础上考虑了时间因素的影响，提出了新进节点与老节点的连接概率正比于老节点连接度和老节点年龄的幂τ-α.他们通过理论分析和数值模拟发现，当α>1时网络的无标度属性消失.2003年，Zhu等[8]也在BA模型的连接概率中引入了与节点年龄相关的指数衰减函数.根据理论分析与数值模拟发现生成的网络除了度分布发生变化之外还有很多明显的变化.另外，Klemm和Eguiluz[9-10]通过研究科学引文网络，观察到了节点年龄和连接概率之间存在负相关.在此基础上，他们考虑了个体的有限集体记忆并提出了一个高聚类系数的无标度网络模型.该模型解释了三种经验特征,偏好连接，幂律分布以及节点年龄与连接概率之间的负相关性.但是在这个模型中，节点一旦老化就再也不能获得新的连接，这个条件太过于绝对.

在真实网络中，广泛存在着老化态节点再次被激活的现象.最近,Xiong等[11]在综合考虑了基于节点个体消耗的老化过程和钝化态节点通过与活性态节点相邻来进行激活的效应，提出了一个带有邻居激活机制的耗散网络模型.在这个模型中，随着新节点的不断加入，活性节点可能疲于相互作用而慢慢地失去活性成为老化态节点.但是，这些老化态节点又有可能通过与活性态节点相邻而被激活.他们通过数值模拟得到了幂律形式的度分布，并且得到了高的聚集系数和度正相关性.

本文在钝化网络模型的基础上，提出了一个带有随机激活行为的钝化网络模型.将网络中节点的状态分为活性态和休眠态两种.在该网络模型中，同时考虑了新进活性态节点不断地加入和老节点状态不断转变的过程.并且就该模型给出了一致的网络度分布的理论与模拟解析结果.

1　网络模型

带有随机激活机制的钝化网络模型描述了带有激活机制的有向增长网络.网络中已有节点的状态分为两种，活性态和休眠态.新加入的节点一开始总是处于活性态，并且发出一定数目的连边.随着网络的演化，活性态节点可能会老化暂时失去活性成为休眠态节点；然而由于某种原因，休眠态节点可能被选择激活再次成为活性态节点.在整个网络演化的过程中，只有活性态节点能够被新进节点连接.下面就网络演化模型进行具体介绍：

1)初始时刻有m0个度为m的节点，其中有m个为活性态节点(这里要求m0>m)，其他节点的状态均为钝化态；

3)激活新进节点i，即新进节点的初始状态为活性态；

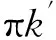
6)返回步骤2，进行演化直到网络尺寸达到N为止.

该模型可以应用于引文网络中，活性态节点通过老化可能成为休眠态节点，这个过程可以认为是一个“遗忘”的过程.休眠态节点也能够通过再次被激活成为活性态节点，从而再次受到关注与新进的活性态节点连接，即再次被新的文献引用，该过程也是一个知识的再认识过程.

2　度分布的理论计算及数值模拟

定义A(k′,t)和D(k′,t)分别为t时刻网络中具有入度为k′的活性态节点和休眠态节点的数目.根据网络的演化过程可以写出网络的演化方程.

对于活性态节点可以写出差分方程

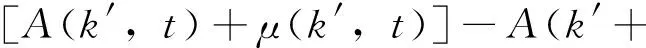
(1)

对于钝化态节点可以写出率方程

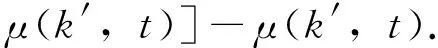
(2)

其中,μ(k′,t)和π(k′,t)分别为t时刻网络中具有入度为k′的节点的激活和钝化的概率.当网络规模足够大时，网络中活性态节点的度分布趋于稳定状态，即

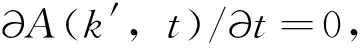
代入(1)式有

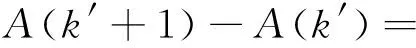
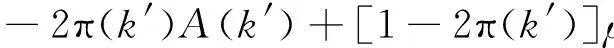
(3)

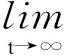
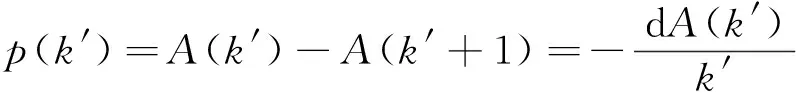
(4)

为了便于分析，本文主要考虑了一种随机激活和偏好钝化的情况.在这种情况下，任意一个休眠态节点被激活的概率均相等，则t时刻入度为t休眠态节点被激活的概率为

(5)

应用极限条件D(k′)=tp(k′)，代入(5)式可得到

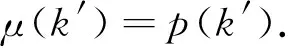
(6)

根据(4)式有

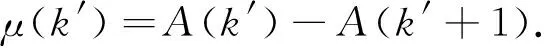
(7)

2.1随机钝化

此处的钝化概率为随机概率，即每个活性态节点被钝化的概率相等，可得

(8)

将(7)式和(8)式代入(3)式得到

(9)

对上述方程进行求解有

(10)

根据初始条件可知A(0)的值为1，即表示新进的活性节点的入度为0.因此，可以得到整个网络的入度分布为

(11)

为了得到网络中节点的整体度分布，这里只需要把上述方程变换成如下的形式

(12)

其中k=k′+m.

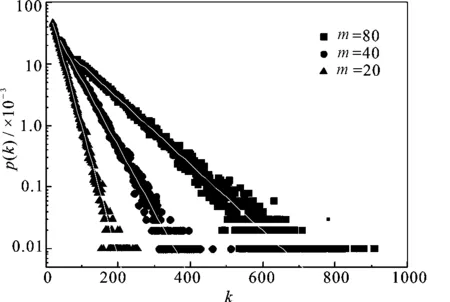
生成网络参数为m0=m+1，生成网络的尺寸为n=105，实线为(12)式的最小二乘法拟合结果

图1度分布的模拟和理论解析解的比较

Fig1Simulatedandtheoreticalresultsofdegreedistribution

图1给出了这种情况下网络规模为105的整个网络的度分布的模拟和理论解析解的结果，通过最小二乘法拟合，得到对应于m=20，40和80的衰减指数1/(m+1)分别为0.048(8),0.024(7)和0.012(4).可以看出网络度分布为指数分布，并且与解析结果完全一致.

2.2偏好钝化

此处采用了偏好钝化机制，即节点被钝化的概率正比于该节点的入度.由此可以得到，当前活性节点j被钝化的概率为

(13)

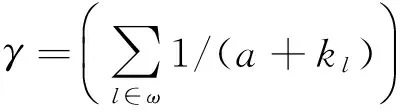
(14)

对上述方程进行求解有

(15)

由初始条件A(0)=1，代入(4)式可得到网络入度的分布为

(16)

根据上式可得网络中节点的整体度分布，这里将上式变换为

(17)

(18)

由上式可以看出，指数γ依赖于a和m的取值.当a=m+2时，γ=2.图2给出了这种情况下网络规模为105的整个网络的度分布的模拟和解析解的结果.通过最小二乘法拟合，得到对应于m=20,40和80的衰减指数γ+1分别为2.83(7),2.91(6)和2.92(9).可以看出网络度分布为幂律分布，并且与理论解析结果完全一致.

3　结束语

钝化网络模型考虑了节点的有限记忆性，能够体现真实世界的许多特性，幂律度分布，高的集团系数和非负的连通相关性.但是钝化网络模型只考虑了不可逆的老化效应，节点从活性态到钝化态的变化是一个绝对钝化过程，而实际情况是钝化态节点也有可能会被重新激活.本文在原有的钝化网络模型的基础上考虑了随机激活机制，采用率方程和差分方程分别对网络中的活性态节点和钝化态节点的演化过程进行了描述，并且找出了这两个演化方程的内在联系.本文就随机钝化和偏好钝化两种情况对网络的度分布进行了理论解析求解和数值模拟.通过最小二乘法拟合，得到了与理论解析解相一致的结果.该模型拓展了原有的钝化网络模型，为网络模型的进一步应用创造了条件.

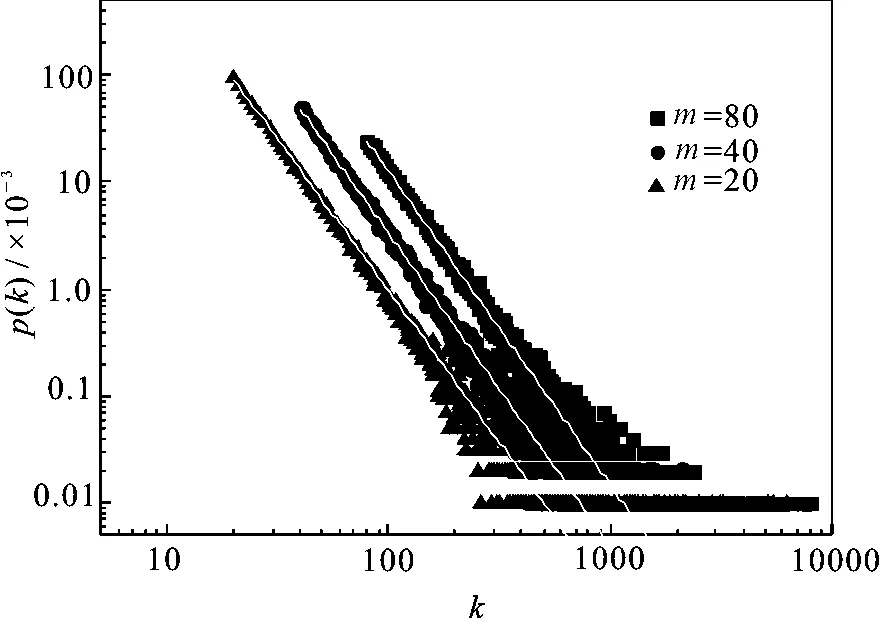
生成网络参数为m0=m+1，α=m+2,生成网络的尺寸为n=105，实线为公式(17)的最小二乘法拟合结果

图2度分布和理论解析解的比较

Fig2Simulatedandtheoreticalresultsofdegreedistribution

[1]ALBERTR,BARABASIAL.Statisticalmechanicsofcomplexnetworks[J].Reviews of Modern Physics,2002,74(1):47.

[2]NEWMAN M E J.The structure and function of complex networks[J].SocietyforIndustrialandAppliedMathematics,2003,45(2):167.

[3]BARABASI A L,ALBERT R.Emergence of scaling in random networks[J].Science,1999,286(15):509.

[4]BARABASI A L,ALBERT R,JEONG H.Mean-field theory for scale-free random networks[J].PhysicaA,1999,272(1-2):173.

[5]DOROGOVTSEV S N,MENDS J F F,SAMUKHIN A N.Structure of growth networks with preferential linking[J].PhysicalReviewLetters,2000,85(21):4633.

[6]SHI D H,CHEN Q H,LIU L M.Markov chain-based numerical method for degree distribution of growing networks[J].PhysicalReviewE,2005,71(3):036140.

[7]DOROGOVTSEV S N,MENDS J F F.Evolution of networks with aging of sites[J].PhysicalReviewE,2000,62(2):1842.

[8]ZHU H,WANG X R,ZHU J Y.Effect of aging on network structure[J].PhysicalReviewE,2003,68(5):056121.

[9]KLEMM K,EGUILUZ V M.Highly clustered scale-free networks[J].PhysicalReviewE,2002,65(3):036123.

[10]KLEMM K,EGUILUZ V M.Growing scale-free networks with small-worid behavior[J].PhysicalReviewE,2002,65(5):057102.

[11]XIONG F,LIU Y,ZHU J,et al.A dissipative network model with neighboring activation[J].TheEuropeanPhysicalJournalB,2011,84(84):115.

(责任编辑孙对兄)

The deactivation network model with random activation mechanism

WANG Xue-wen1,LUO Yue-e1,PAN Wei-wei1,YANG Feng2

(1.School fo Physics and Electronic Sciences,Guizhou Normal College,Guiyang 550018,Guizhou,China; 2.School of Mechanical and Electronic Engineering,Jingdezhen Ceramic Institute,Jingdezhen 333403,Jiangxi,China)

In the general deactivation network model,the state change of node is an absolutely deactivation process,it is an irreversible aging process.Considering the actual situation,an inactive node will be reactivated again and become an active node in some cases,this paper presents a deactivation network model with random activation behavior,and the finite difference equations and rate equations are used for describing network evolution process of the active node and dormant node respectively.This paper gives the network degree distributions of the theory analytical solution and numerical simulation,and obtains the consistent results.

deactivation network;deactivation;activation;degree distribution.

10.16783/j.cnki.nwnuz.2016.05.012

2016-04-23;修改稿收到日期:2016-07-29

贵州省教育厅自然科学研究项目(黔教合KY字[2015]355)；贵州师范学院自然科学研究基金项目(13BS013,13BS012)；贵州省科技厅自然科学研究项目 黔科合J字([2014]2143号)；江西省学位与研究生教育教学改革研究项目(JXYJG-2015-091)

王学文(1976—)，男，江西景德镇人，副教授,博士.主要研究方向为复杂系统与复杂网络.

E-mail:icewater0397@163.com

N 94

A

1001-988Ⅹ(2016)05-0051-04