广义Virasoro代数到中间序列模的导子

方政蕊

(武夷学院数学与计算机学院，福建武夷山　354300)



广义Virasoro代数到中间序列模的导子

方政蕊

(武夷学院数学与计算机学院，福建武夷山354300)

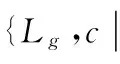
广义Virasoro代数； 中间序列模； 导子；1-上同调群

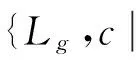
(1)

其中L0=CL0Cc,Lg=CLg(g≠0).

李代数导子的研究是李理论中的一个重要课题，因为导子与李代数的低阶上同调群有密切联系，李代数定义关系中看不出的一些结构特性往往能随着导子的确定而洞察.近年来，很多代数的导子已被广泛研究，2006年Ren等[9]研究了扭Heisenberg-Virasoro代数的导子代数和自同构群；高寿兰等[10]研究了无中心的Virasoro李代数(即witt代数)的一类扩张李代数的结构，并给出了它的导子代数.对于导子研究的文献还有很多[11-13].

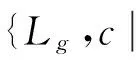
1　相关概念

本文讨论复数域C上的李代数，设G为复数域C的任意非零加法子群.下面先给出本文要用到的一些基本概念.

定义1.1[15]如果李代数L有子空间直和分解L=g∈GLg，使得∀g,h∈G，都有[Lg,Lh]⊆Lg+h，那么称L是G-阶化李代数.

定义1.2[15]设L是G-阶化李代数，W是L-模.如果W有子空间直和分解W=g∈GWg，使得∀g,h∈G，都有Lg·Wh⊆Wg+h，那么称W是G-阶化L-模.

定义1.3[15]设L是G-阶化李代数，W是L-模，φ:L→W是一个线性映射.如果∀x,y∈L，都有

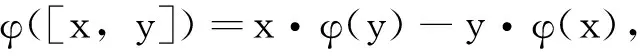
那么称φ是L-模W的导子，简称W的导子.∀ν∈W，线性变换Dν:x|→x·ν是W的导子，称为W的内导子；不是内导子的导子称为外导子.W的导子全体构成的集合记为Der(L,W)，内导子全体构成的集合记为DerInn(L,W).

记H1(L,W)为李代数L到L-模W上的一阶上同调群，则有

引理1.1[15]设L=g∈GLg是有限生成的G-阶化李代数，W=g∈GWg是G-阶化L-模，则Der(L,W)也是G-阶化的，即有：

Der(L,W)=g∈GDer(L,W)g,

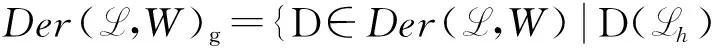
引理1.2[14]设L=g∈GLg是有限生成的G-阶化李代数，W=g∈GWg是G-阶化L-模.如果

1)H1(L0,Wg)=0,∀g∈G{0}；

2)HomL0(Lg,Wh)=0,∀g≠h，那么，Der(L,W)=Der(L,W)0+DerInn(L,W).

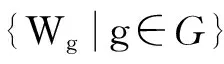
Aa,b(G): Lgwh=(a+h+gb)wg+h;

Aa(G): Lgwh=(h+g)wg+h,h≠0;

Lgw0=g(g+a)wg;

Ba(G): Lgwh=hwg+h,h≠-g,

Lgw-g=-g(g+a)w0;

其中g,h∈G，c在Aa,b(G),Aa(G),Ba(G)上的作用都为0.

对于引理1.3中L的三类中间序列模及子商模，有以下同构关系：

(i)Aa,b(G)≅Aa′,b(G),a-a′∈G;

(ii)Aa,0(G)≅Aa′,1(G),a∉G,a-a′∈G;

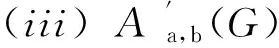
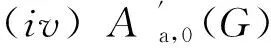
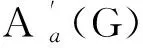
下面讨论广义Virasoro代数到三类中间序列模的导子，记广义Virasoro代数为L.

2　L到模Aa,b(G)的导子

由于∀a,a′∈C，当a-a′∈G时，有Aa,b(G)≅Aa′,b(G)，因此，可以假定a∉G或a=0.记W=Aa,b(G)，则W=g∈GCwg，且

定义L到W的4个线性映射如下：

容易验证这4个线性映射和Dw0具有如下性质，其中Dw0为内导子.

性质2.1(1)当a=0,b=1时，θ1∈Der(L,Wg)0，且θ1,Dw0线性无关；

(2)当a=0,b=2时，θ2∈Der(L,Wg)0，且θ2,Dw0线性无关；

(3)当a=0,b=2时，Dw0=0,θ3,θ4∈Der(L,Wg)0，且θ3,θ4线性无关；

引理2.1对∀g∈G，当g≠0时，有H1(L0,Wg)=0.

证明设D∈Der(L0,Wg),∀x∈L0，将D作用等式0=[L0,x]，得

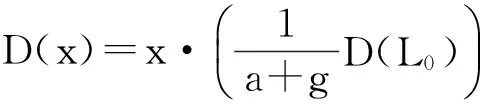
引理2.2对∀g,h∈G，当g≠h时，有HomL0(Lh,Wg)=0.

证明设φ∈HomL0(Lh,Wg),∀x∈Lh,φ(x)∈Wg.将φ作用等式hx=[L0,x]，得

移项得(a+g-h)φ(x)=0.由于a∉G或a=0，且g≠h，所以a+g-h≠0，进而有φ(x)=0.由此得φ=0，所以HomL0(Lh,Wg)=0.

由引理2.1,引理2.2以及文献[14]的命题1.2，可得命题2.1.

命题2.1Der(L,W)=Der(L,W)0+DerInn(L,W).

由命题2.1，只需计算Der(L,W)0.为此，下面分5种情况进行计算.

引理2.3当a≠0时，Der(L,W)0⊆DerInn(L,W).

证明任取D∈Der(L,W)0，对∀x∈Lg，有D(x)∈Wg.将D作用等式gx=[L0,x]，得

整理得

引理2.4当a=0, b≠0,1,2时，DerInn(L,W)0⊆DerInn(L,W).

证明任取D∈Der(L,W)0，对∀g∈G{0}，将D分别作用等式gLg=[L0,Lg]和0=[c,Lg]，得

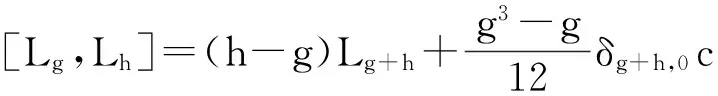
在上式中比较wg+h的系数，可得

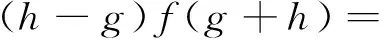
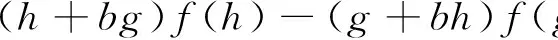
(2)

进一步地，在(2)中，用-g替换h，有

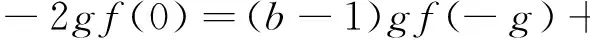
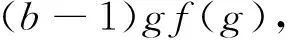
(3)

利用(3)式及b≠1的条件，可得

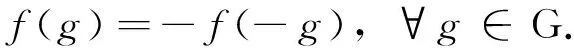
(4)

在(2)式中，取h=1，可得

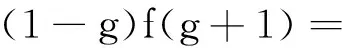
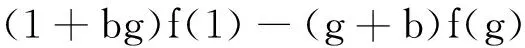
(5)

在(2)式中，取h=-1，并用g+1替换g，可得

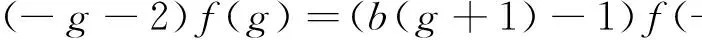
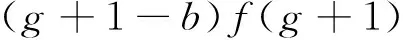
(6)

联立(5)，(6)式，消去f(g+1)，并利用(4)式有f(1)=-f(-1)，可得，

当b≠-1时，利用b≠2的条件消去2+b-b2，可得f(g)=gf(1)；

注意到，将b=-1代入(5)，(6)式中，也可得，f(g)=gf(1)，所以取k=f(1)，即得到

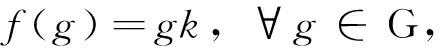
即

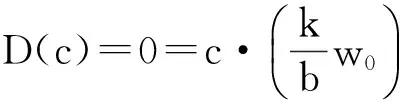
Der(L,W)0⊆DerInn(L,W).

引理2.5当a=0,b=1时，Der(L,W)0=Cθ1CDw0.

证明由性质2.1，只需证明Der(L,W)0⊆Cθ1CDw0.任取D∈Der(L,W)0，由引理2.4的证明可得，D(L0)=D(c)=0.对∀g∈G，设D(Lg)=f(g)wg，有f(0)=0.

将b=1代入(5)，(6)式，可得

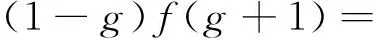
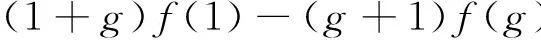
(7)

(8)

联立(7)，(8)式，消去f(g+1)，可得

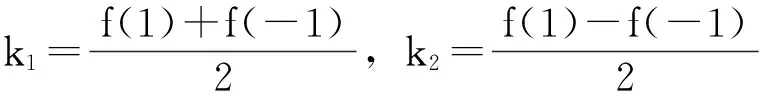
即得到f(g)=k1g2+k2g，

因此，D(Lg)=f(g)wg=k1g2wg+k2gwg,

由于k2gwg=Lg·w0，所以

因此Der(L,W)0⊆Cθ1CDw0，从而，Der(L,W)0=Cθ1CDw0.

引理2.6当a=0,b=2时，Der(L,W)0=Cθ2CDw0.

证明由性质2.1，只需证明Der(L,W)0⊆Cθ2CDw0.任取D∈Der(L,W)0，由引理2.4的证明可得，D(L0)=D(c)=0.对∀g∈G，设D(Lg)=f(g)wg，有f(0)=0.

将b=2 代入(2)式，可得

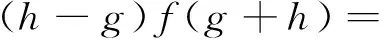
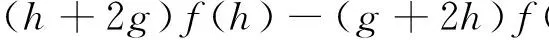
(9)

进一步地，在(9)式中，用-g替换h，可得

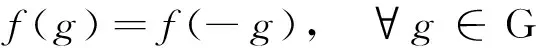
(10)

即f(1)=f(-1),f(2)=f(-2)

在(9)式中，取h=1，可得

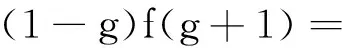
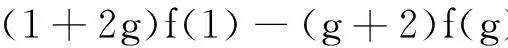
(11)

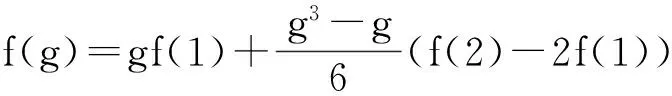
取f(1)=2k1,f(2)-2f(1)=k2，即得到

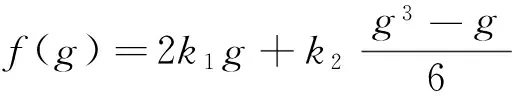
因此D=k1Dw0+k2θ2，所以

从而

Der(L,W)0=Cθ2CDw0

引理2.7当a=0,b=0时，Der(L,W)0=Cθ3Cθ4.

证明由性质2.1，只需证明Der(L,W)0⊆Cθ3Cθ4.任取D∈Der(L,W)0，对∀g∈G，设D(Lg)=f(g)wg，将b=0代入(5)，(6)式，可得

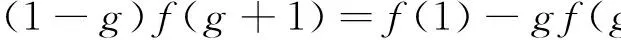
(12)

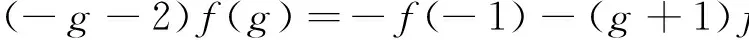
(13)

联立(12)，(13)式，消去f(g+1)，可得

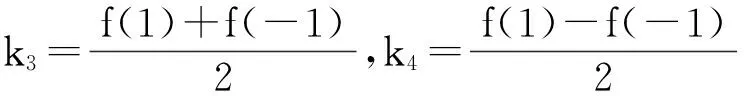
所以D=k3θ3+k4θ4，Der(L,W)0⊆Cθ3Cθ4，从而Der(L,W)0=Cθ3Cθ4.

由命题2.1和引理2.3～2.7，可得下面的定理.

定理2.1设W=Aa,b(G)有

(1)当a∉G时，Der(L,W)=DerInn(L,W)；

(2)当a=0,b≠0,1,2时，Der(L,W)=DerInn(L,W)；

(3)当a=0,b=1时，Der(L,W)=DerInn(L,W)Cθ1；

(4)当a=0,b=2时，Der(L,W)=DerInn(L,W)Cθ2；

(5)当a=0,b=0时，Der(L,W)=DerInn(L,W)Cθ3Cθ4；

推论2.1

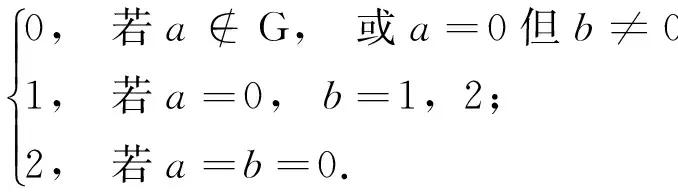
3　L到模Aa(G)的导子

由文献[8]中关于模的同构关系可知，A0(G)≅A0,1(G)，下面只对a≠0的情形进行讨论.

记W=Aa(G)，则W=g∈GCwg，且

Lgw0=g(g+a)wg.

性质3.1定义L到W的线性映射为：Ψ(Lg)=gwg,Ψ(c)=0.则当a≠0时，这个线性映射Ψ∈Der(L,Wg)0，且Ψ，Dw0线性无关，其中Dw0为内导子.

引理3.1对∀g∈G，当g≠0时，有H1(L0,Wg)=0.

证明设D∈Der(L0,Wg),∀x∈L0，则D(x)∈Wg, D(c)∈Wg，

设D(x)=f(g)wg，对∀g∈G，当g≠0时，有

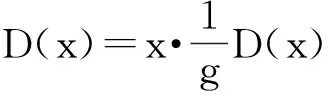
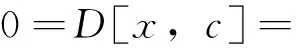
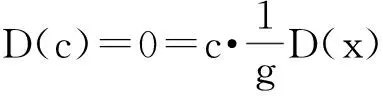
引理3.2对∀g,h∈G，当g≠h时，有HomL0(Lh,Wg)=0.

证明设φ∈HomL0(Lh,Wg),∀x∈Lh,φ(x)∈Wg.将φ作用等式hx=[L0,x]，得

gφ(x)=hφ(x),

经移项得

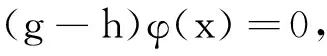
对∀g,h∈G，当g≠h时，有g-h≠0，所以φ(x)=0，由此得φ=0，所以HomL0(Lh,Wg)=0.

由引理3.1、引理3.2以及文献[14]的命题1.2，可得命题3.1.

命题3.1Der(L,W)=Der(L,W)0+DerInn(L,W).

由命题3.1，只需计算Der(L,W)0.

引理3.3Der(L,W)0=CΨCDw0.

证明由性质2.1，只需证明Der(L,W)0⊆CΨCDw0.任取D∈Der(L,W)0，对∀g∈G，设D(Lg)=f(g)wg,D(c)=c0w0.

将D作用于[L-1,c]=0和[L1,L-1]=-2L0上，可得c0=f(0)=0.

当g≠0,-1时,

将D作用于[L-1,Lg+1]=(g+2)Lg和[L1,Lg]=(g-1)Lg+1上，可得

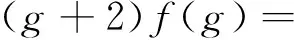
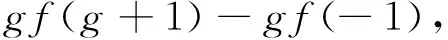
(14)

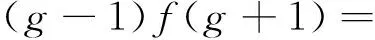
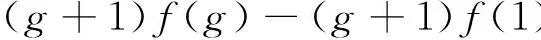
(15)

联立(14)，(15)式，可得

(16)

显然，(16)式对g=0,-1也成立，从而对任意g成立.

因此

从而Der(L,W)0⊆CΨCDw0.

综上所述，Der(L,W)0=CΨCDw0.

由A0(G)≅A0,1(G)，可知当a=0时，L到模A0(G)的导子与模A0,1(G)的导子结构相同，所以由定理2.1以及引理3.3有以下定理.

定理3.1Der(L,A0(G))=CΨDerInn(L,A0(G)).

推论3.1dimH1(L,A0(G))=1.

4　L到模Ba(G)的导子

由文献[8]中关于模的同构关系可知，B0(G)≅A0,0(G)，下面只对a≠0的情形进行讨论.

记W=Ba(G),a≠0，则W=g∈GCwg，且

定义L到W的线性映射θ1,θ2如下：

容易验证两个线性映射具有如下性质：

性质4.1θ1,θ2∈Der(L,Wg)0,且θ1,θ2线性无关.

因为L0和c在Aa(G)和Ba(G)的基元wg上的作用相同，所以引理3.1和引理3.2对于模Ba(G)也成立.于是可直接得出以下两个引理.

引理4.1对∀g∈G，当g≠0时，有H1(L0,Wg)=0.

引理4.2对∀g,h∈G，当g≠h时，有HomL0(Lh,Wg)=0.

由引理4.1、引理4.2以及文献[14]的命题1.2，可得命题4.1.

命题4.1Der(L,W)=Der(L,W)0+DerInn(L,W).

由命题4.1，只需计算Der(L,W)0.

引理4.3Der(L,W)0=Cθ1Cθ2.

证明由性质4.1知，θ1和θ2线性无关，只需证明Der(L,W)0⊆Cθ1Cθ2，任取D∈Der(L,W)0，对∀g∈G，设D(Lg)=f(g)wg,D(c)=c0w0.

当g+h≠0时，

由D[Lg,Lh]=Lg·D(Lh)-Lh·D(Lg),得

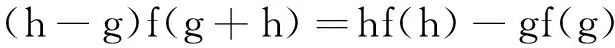
(17)

将g=1代入(17)式，得

其中h≠-1.

再将g=-1代入(17)式，并用h+1替换h，得

其中h≠0.因此，可得到

(18)

由(18)式可得，对任意的h≠0，有

从而

下面求D(L0)和D(c).

由D[L-1,L1]=L-1·D(L1)-L1·D(L-1),得

所以

最后，由于

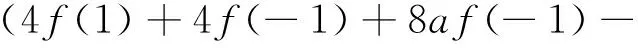
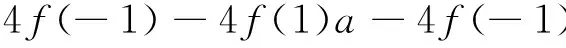
16f(1)a-16f(-1)a)w0=

因此

进而Der(L,W)0⊆Cθ1Cθ2.

由B0(G)≅A0,0(G)，可知当a=0时，L到模B0(G)的导子与模A0,0(G)的导子结构相同，所以由定理3.1以及引理4.3，有以下定理：

定理4.1Der(L,Ba(G))=Cθ1Cθ2DerInn(L,Ba(G)).

推论4.1dimH1(L,Ba(G))=2.

[1]KAPLANSKY I,SANTHAROUBANE L.Harish-Chandra Modules over the Virasoro Algebra[M].NewYork:Springer，1985:217.

[2]SU Y C.Classification of Harish-Chandra modules over the higher rank Virasoro algebras[J].CommunicationsinMathematicalPhysics，2003，240(3):539.

[3]HU N H.q-Witt Algebras，q-Lie Algebras，q-Holomorph structure and representations[J].AlgebraColloquium，1999，6(1):51.

[4]HU N H.Quantum group structure of the q-deformed Virasoro algebra[J].LettersinMathematicalPhysics，1998，44(2):99.

[5]MAZORCHUK V，ZHAO K M.Classification of simple weight Virasoro modules with a finite-dimensional weight space[J].JournalofAlgebra，2005，307(1):209.

[6]MAZORCHUK V.On simple mixed modules over the Virasoro algebra[J].MatematychniStudii，1999，22(2):121.

[7]MATHIEU O.Classification of Harish-Chandra modules over the Virasoro Lie algebra[J].InventionesMathematicae，1992，107(1):225.

[8]SU Y C，ZHAO K M.Generalized Virasoro and super-Virasoro algebras and modules of intermediate series[J].JournalofAlgebra，2003，252(1):1.

[9]REN S，JIANG C B.The derivation algebra and automorphism group of the twisted Heisenberg-Virasoro algebra[J].CommunicationsinAlgebra，2006,34(7):2547．

[10]高寿兰，姜翠波，裴玉峰．一类 Lie 代数的导子及中心扩张与自同构[J].数学学报，2009(2):281．

[11]姜翠波，杨国庆．无限维 Heisenberg 代数的导子代数[J].烟台师范学院学报(自然科学版)，1996(2):85．

[12]JIANG C B ,MENG D J.The Automorphism group of the derivation Algebra of the Virasoro-like Algebra[J].AdvancesinMathematics,1996，2(2):175.

[13]方政蕊，连海峰.扭 Heisenberg-Virasoro代数到中间序列模的导子[J].四川师范大学学报(自然科学版)，2011，34(4):509.

[14]FARNSTEINER R.Derivations and central extensions of finitely generated Graded Lie Algebras[J].JournalofAlgebra，1988，118(1):33.

[15]汉弗莱斯J E．李代数及其表示理论导引[M].上海:上海科技出版社，1981.

(责任编辑陆泉芳)

The derivations from the generalized Virasoro algebra to its intermediate series modules

FANG Zheng-rui

(Department of Mathematics and Computer，Wuyi College，Wuyishan 354300，Fujian,China)

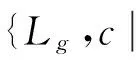
generalized Virasoro algebra;modules of the intermediate series;derivations;the first cohomology group

10.16783/j.cnki.nwnuz.2016.05.009

2016-05-09;修改稿收到日期:2016-07-20

国家自然科学基金资助项目(11571145)；武夷学院青年专项基金资助项目(XQ201107)

方政蕊(1978—)，女，福建武夷山人，讲师，硕士.主要研究方向为李代数.E-mail:fzr1117@163.com

O 152.5

A

1001-988Ⅹ(2016)05-0036-06