“身无彩凤双飞翼，心有灵犀一点通”——用“坐标法”教学曲线

□ 江苏省苏州市吴中区临湖第一中学 柳春喜

“身无彩凤双飞翼，心有灵犀一点通”
——用“坐标法”教学曲线

□ 江苏省苏州市吴中区临湖第一中学 柳春喜

“能理乱丝，乃可读诗。”（明·杨慎《古今谚》）其大意是：能够整理纷乱的思绪，才可以开始读诗作文。它讲述这样一个道理：只有能在纷乱的现象中剔除芜杂，抓住本质，整理思绪的人，才有可能读懂古训，付之实践。同样，初中数学中抛物线、双曲线问题，只要你抓住其本义，何愁解不出来呢！

解析几何区别于综合几何的最本质特征是它的研究方法，即坐标法。正因为笛卡尔建立了平面坐标系，才得以用代数方法研究几何问题。因此，我们说坐标化方法是解析几何的本质特征，没有坐标化，就没有解析几何这门学科。虽然解析几何的体系建立以后，其研究的对象更加多样了，研究的内容更加丰富了，研究的方法更加灵活了，认识的程度更加深刻了，但是“坐标化”始终是它不变的灵魂。历年的高考中，尽管解析几何试题的载体可能是直线、圆、椭圆、双曲线或抛物线，形式也可以多变，但是根本宗旨还是考查坐标化方法和坐标化思想。

一、曲线的核心组成——点

对于一个几何问题，在建立坐标系的基础上，用坐标表示点；用方程表示曲线，通过研究方程的性质间接地来研究曲线的性质，这一研究几何问题的方法称为坐标法。我们初中的重点是：用坐标表示点、点再连成平滑曲线。所以双曲线、抛物线背景下的本义是“点的坐标”。只要我们把点的坐标解决了，问题随之完成。

例1：如图，在平面直角xOy坐标系中，四边形OABC是正方形，点A，C的坐标分别为（2，0）、（0，2），D是x轴正半轴上的一点（点D在点A的右边），以BD为边向外作正方形BDEF （E、F两点在第一象限），连接FC交AB的延长线于点G.

（1）若AD=1，求点F的坐标；

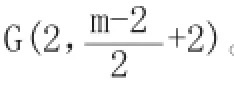
这正如北京教育考试院王雅琪老师所说“坐标一桥飞架，数形天堑变通途”。美籍匈牙利数学家波利亚曾说过：“类比是一个伟大的引路人。”19世纪俄国教育家，被称为“俄罗斯教育心理学的奠基人”乌申斯基也说过：“比较是一切理解和思维的基础。”的确，比较的思想方法在中学数学教学和学习中有着无可替代的优越性。它既是一种逻辑方法，也是一种科学研究的方法，是最重要的数学思想方法之一。运用这种方法，能突出数学问题的本质特征，同时加强了数学教学的艺术效果和感染力。

二、比较中生成情愫

例2：抛物线y=x2-4x-5与y轴交于点C，交x轴于A、B两点（A在B的左侧），已知点M是抛物线上一动点，当⊿MBC的面积为10时，求点M的坐标。

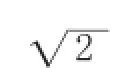
解：令y=0则x2-4x-5=0

解之得：x1=-1，x2=5

所以点B（5，0）

令x=0则y=-5

所以点C（0，-5），OB=OC=5，⊿

所以k=1，b=-5，直线BC解析式为y=x-5，由它上下平移4个单位得两直线分别是：y=x-1和y=x-9

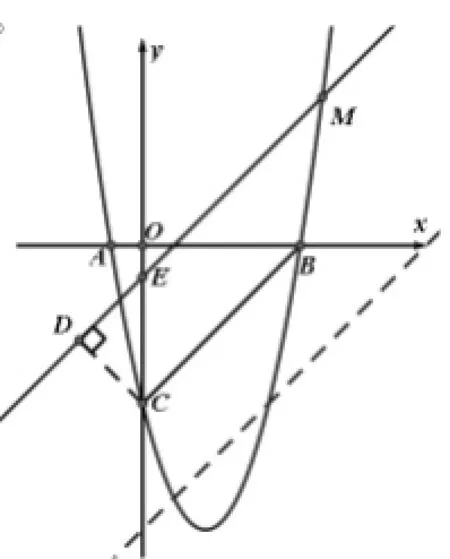
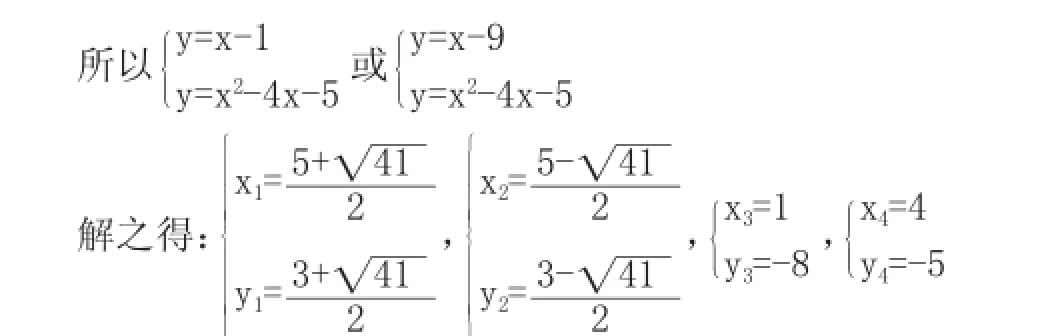
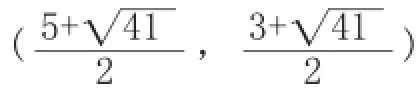
感悟：

这样的直线有两条，千万不要漏解。另外，平行线间的距离若能转化到它们在轴上所夹线段的长度，那么利用平移知识很快就能构造直线解析式，利于解决问题。从形到数再到形，此法我以为在审题要注意充分揭示图形的几何特征，即图形的内在性质，运用相关的几何结论，直接转化到解析法（列出方程组）解题，这样思路直接、解法简捷、过程简化。

“解法比较”：

设点M（x，x2-4x-5），易得B（5，0），即Bx=5；直线BC解析式为：y=x-5.

（1）当M在BC下方时（如图），过点M作MP∥y轴交BC于P，

则P（x，x-5），MP=Py-My=x-5-（x2-4x-5）=5x-x2

由于 S△MBC=10，所以 S △CPM+S△MPB=10，即PM·P+XPM（BX-PX）=10

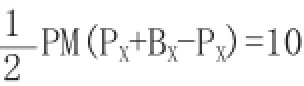
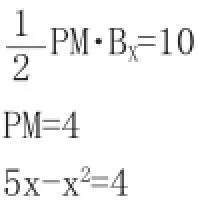
解之得：x1=1，x2=4即M（1，-8）或M（4，-5）

（2）当点M在BC上方时（如图），过M’作M’Q∥y轴，交BC所在的直线于点Q，则Q（x，x-5），M’Q=（x2-4x-5）-（x-5）=x2-5x由于S△M’BC=10，所以S△CQM’-S△M’QB=10

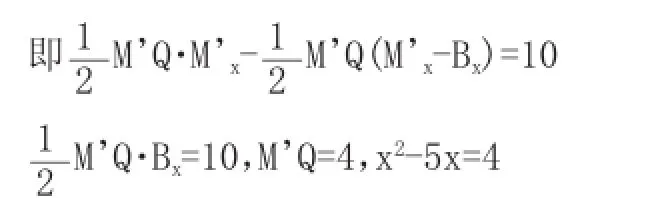
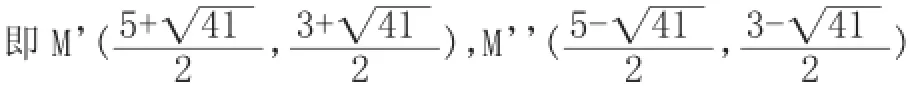
感悟：通过组成抛物线的核心，解设动点坐标，再把该坐标转化成有关线段，利用面积这一条件列出方程，我想这也是解决曲线上动点的一个有效方法。追求解题过程的多样化、思维过程的严谨性是解题者的天性，这也是培养学生创新意识、科学意识的一种有效途径.

三、数学思想使学生产生“火花”，并成为思考问题的常态

著名数学家华罗庚说：新的数学方法和概念，常常比解决数学问题本身更重要。传授数学知识、演化数学方法、传承数学文化是数学教育的重要任务，串联数学知识、数学方法与数学文化的“经脉”是数学思想。可以说，数学教育的本质就是数学思想的教育，掌握了数学思想，就是掌握了数学的精髓。让我们再看一例。

例3：（2015山东济宁中考题）如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点 （点A在点B的上方），与x轴的正半轴相交于点C；直线l的解析式为y=3x+4，4 与x轴相交于点D；以C为顶点的抛物线经过点B.

（1）求抛物线的解析式；

（2）判断直线l与⊙E的位置关系，并说明理由；

（3）动点P在抛物线上，当点P到直线l的距离最小时，求出点P的坐标及最小距离。

分析：（1）我们可由点E坐标转化出OE=3，由半径为5转化出点C（8，0），连结EB，在Rt△OEB中，用勾股定理易得OB=4，于是点B（0，-4），然后假设抛物线的顶点式易得：y=-x-8）2这里就充分展示了数形结合的思想，并用到了勾股定理。

（2）可由直线解析式得出点A、点D坐标，易得EA、AD、DE三线段的长，再由勾股定理的逆定理不难说明EA⊥直线l。

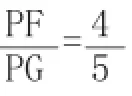
感悟：从数（点的坐标）到形（线段），然后利用几何知识处理后，再到数，直到解决问题，这种解法思路简捷、直观，但构造法较难。在我们平常的教学中，要把数学思想与相应的数学知识联系起来理解，揭示内涵；要追根溯源，刨根问底，积极展示数学思想发生、形成的过程，进而多角度、多层次地理解数学思想；要让数学思想生活化，把数学思想渗透到学生生活中，培养学生自觉用数学思想解决生活中的问题的数学意识。

总之，曲线上的动点问题是个让学生头痛的问题，也是各地中考的常见问题。我们在解这类题时要多思维、善联想、寻方法、巧转化，使其形成自觉的转化意识、数形结合意识、构造意识，从而培养学生的应变能力和创造思维能力，提高学生用数学思想解决数学问题的能力。