引入超前-滞后校正的数字滤波器优化设计

郭喜峰　栾方军　刘美菊　李云路　刘　剑

(沈阳建筑大学信息与控制工程学院1，辽宁 沈阳　110866；东北大学信息科学与工程学院2 ，辽宁 沈阳　110819)



引入超前-滞后校正的数字滤波器优化设计

郭喜峰1栾方军1刘美菊1李云路2刘剑1

(沈阳建筑大学信息与控制工程学院1，辽宁 沈阳110866；东北大学信息科学与工程学院2，辽宁 沈阳110819)

为满足有源电力滤波器谐波检测的需要，提出同时加入超前和滞后校正改善低通滤波器特性的优化设计。在比较各种滤波器后，选取二阶椭圆型滤波器作为谐波检测的核心；通过分析系统零极点的分布，得出影响系统性能的参数配置关系，并加入超前-滞后校正，对数字低通滤波器进行优化。仿真试验表明，该优化设计方法能够更好地满足电网谐波和基波无功电流检测的需要，使检测系统同时获得良好的检测精度和令人满意的动态响应速度。

超前校正滞后校正谐波检测数字低通滤波器有源电力滤波器优化

0　引言

有源电力滤波器(activepowerfilter,APF)是有效抑制谐波的重要手段。具有较好实时性和准确性的谐波检测系统是APF消除谐波、补偿无功的前提，谐波检测算法的优越性是APF正常工作的基本保障，数字低通滤波器(lowpassfilter,LPF)的合理性将直接决定谐波检测系统的工作性能[1-3]。

文献[4]提出数字低通滤波器的设计，给出基本的选型和阶次，但没对数字低通滤波器响应时间进行分析。文献[5]设计的数字低通滤波器具有预测功能，但从试验结果可以看出，基波信号提取平滑度不高，含有部分高次谐波成分。文献[6]中研究了巴特沃斯数字低通滤波器的截止频率和调整时间的关系，试验数据较详细，但没有对其他类型的数字低通滤波器进行研究。文献[7]中的数字低通滤波器是通过双神经网络实现的，并给出了系统稳定状态下的波形图，但未给出系统稳定前的波形图。文献[8]提出基于校正网络的谐波检测方法，即加入超前校正的巴特沃斯数字低通滤波器，使系统得到较快的响应速度；但文中没有对校正网络进行稳态分析，加入超前校正后需要综合考虑，因为动态响应较快的同时也会加大系统的超调和稳态误差。

本文选取二阶椭圆滤波器，加入超前-滞后校正对数字低通滤波器进行优化，并对不同类型滤波器加入校正前后的情况进行仿真和试验比较。比较结果表明，基于超前-滞后校正的优化设计使整个检测系统具有良好的检测精度和令人满意的动态响应速度，提高了APF的补偿能力，也验证了本文方法的有效性。

1　基于ip-iq理论的谐波电流检测原理

ip-iq谐波检测法是在瞬时功率理论的基础上发展并获得应用的。在三相电路谐波电流检测中，首先将三相信号变换为互相垂直的两相信号[9-11]。

(1)

式中：ia、ib、ic分别为各相电流的瞬时值；ip、iq分别为瞬时有功电流和瞬时无功电流。

当电网电压对称无畸变时，有：

(2)

ip、iq经过低通滤波器后，得到：

(3)

对式(3)求逆变化，可得：

(4)

式中：iaf、ibf、icf分别为检测电流ia、ib、ic的基波分量。将检测的三相电流信号减去基波信号，便得到谐波电流信号。

基于ip-iq法谐波检测原理如图1所示。当iq为零时，补偿所有的无功分量；否则不对无功分量进行补偿。

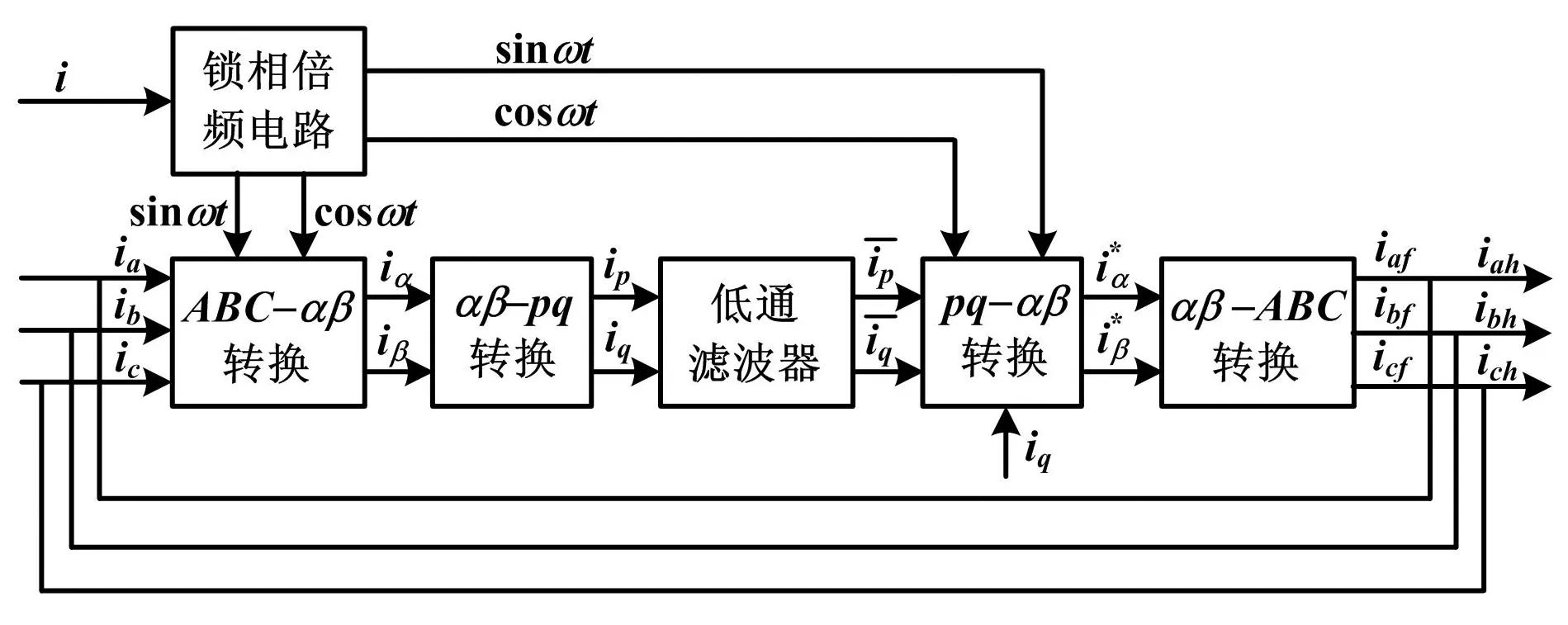
图1　基于ip-iq法谐波检测原理图

2　数字低通滤波器的优化设计

2.1数字低通滤波器

基于瞬时无功功率理论检测谐波和基波无功电流的方法，都要用数字低通滤波器从总的有功电流和无功电流中获取直流分量[2]。很明显，LPF的性能将直接决定检测方法的精确性和动态跟踪速度，并最终影响APF的谐波补偿性能[9-11]。常用的数字低通滤波器主要类型有：巴特沃斯(Butterworth)数字低通滤波器、切比雪夫(Chebyshev)Ⅰ型和Ⅱ型数字低通滤波器、椭圆(Elliptic)滤波器等。不同滤波器的滤波效果如图2所示。图2(a)是信号s=3+0.2sin(300πt)+0.11sin(300πt)在通过频率、截止频率分别为30Hz和50Hz，通带衰减、阻带衰减分别为1dB和80dB下的滤波效果。根据负载谐波特性分析，对要滤波的谐波信号主要成分进行重构，用以检验各种不同滤波器的滤波效果。图2(b)是在相同条件下一阶至五阶椭圆数字低通滤波器的滤波效果。图2(c)是不同通过频率的二阶、三阶椭圆数字滤波器的滤波效果。

图2　不同滤波器滤波效果图

从图2(a)可以看出，ChebyshevⅡ滤波器具有最快的动态响应，Elliptic滤波器次之，Butterworth滤波器最慢。但Elliptic滤波器在线性相位、衰减斜率及加载特性等方面具有特性均衡的特点[12]。

从图2(b)可以看出，椭圆滤波器阶次越高，需要的稳定时间越长，相应的上升时间越长；奇数次滤波结果没有幅值衰减，而偶数次有一定衰减。当稳态误差e≤5%时，一阶动态效果最好，tr为0.006 7s；当e≤1%时，二、三阶次均满足要求。

综上比较，选取30～50Hz作为通过频率。

2.2加入校正的优化设计

以本文选取的椭圆低通滤波器为基础，选取二阶低通滤波器，通带纹波1dB，阻带衰减为80dB，截止频率为30Hz，得到其传递函数H(s)为：

(5)

根据图1，低通滤波器的传递函数为H(s)，被检测三相电流的拉氏变换为I(s)，检测得到的谐波电流拉氏变换为If(s)，有：

If(s)=[E-C23CC32H(s)]I(s)

(6)

式中：E为三阶单位矩阵。

基于ip-iq电流检测方法的传递函数G(s)为：

G(s)=1-H(s)

(7)

将式(6)代入式(7)，传递函数为：

(8)

根据传递函数，得出椭圆滤波器开环和闭环的零极点分布情况，如图3所示。图3中，P、Z表示零极点。

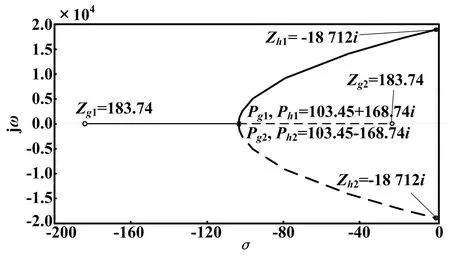
图3　电流检测零极点分布

通过图3可以看出，谐波检测系统的一对零点离原点较远，导致系统的动态响应慢，并且系统开环传递函数的零点位于虚轴之上。在不改变系统稳定性(即不改变系统极点)的情况下，使校正后的系统极点位于坐标原点附近，这样检测系统就具有较好的动态响应性能。

本文选取的超前校正传递函数为：

(9)

滞后校正传递函数为：

(10)

式中：α>1；β>1。

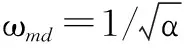
(11)

由于系统的主导极点是-103.45±168.74 i，为不影响系统的频率响应特性，所以增加的滞后开环零点不能影响主导极点。这里，取主导极点10倍距离的点为1 034，那么Tg= 9.67×10-4s。取β=10，得到滞后校正网络传递函数Gg(s)为：

(12)

校正后的传递函数为Hc(s)=H(s)Gd(s)Gg(s)，加入校正的谐波检测原理如图4所示，优化后系统零极点分布如图5所示。

图4　校正后ip-iq法谐波检测原理图

图5　校正后电流检测零极点分布

3　仿真验证

根据以上分析结果，利用Matlab建立仿真模型。选取的巴特沃斯二阶低通滤波器超前校正网络参数为(0.007 5s+1)/(0.000 075s+1)，椭圆滤波器校正详见式(11)、式(12)，待滤波的信号为s(t)= 2.932×sin(200πt)+1.331sin(300πt)，在0.15s进行直流电流幅值切换。不同滤波器的校正网络动态响应曲线如图6所示。图6中：椭圆滤波器加超前-滞后校正上升时间为tr=18ms、超调量σ=1.2%、稳态误差为e≤1.1%，可获取更好的动态性能；只是稳态误差相对于椭圆滤波器加滞后校正略大，但是具有更快的动态响应，可见通过优化提高了系统谐波检测的性能。

利用Matlab搭建三相不可控整流谐波源。仿真电路的主要参数有：电源频率为50Hz、交流电压为78V、阻抗为0.1Ω、感抗为0.1mH、限流电阻为18Ω、电抗为1mH。不可控整流部分电阻为5.4Ω、电感为1mH、电容为1 000μF。限流电阻在0.002s切换，在0.1s时增加一个并联1Ω的负载。仿真精确性分析见表1。

图6　不同滤波器校正网络动态响应曲线

滤波器+校正方法第二周波基波幅值/A误差/%总谐波失真/%椭圆滤波器+超前—滞后校正6.828+0.520.44椭圆滤波器+超前校正6.996+2.511.12巴特沃斯滤波器+超前校正6.032-11.631.51椭圆滤波器+滞后校正6.778-0.660.42

由表1可以看出，椭圆滤波器加超前-滞后校正的优化方法相比巴特沃斯加超前校正，动态响应快且测量精确，对负载电流变化反应更迅速；同时，具有超前校正和滞后校正的优点，因此检测效果更好。

4　试验验证

为了验证加入超前-滞后校正的优化数字低通滤波器的可行性和实用性，利用试验样机进行试验验证。样机核心采用的是TI公司32位浮点数字信号处理器TMS320F28335。样机其他试验参数有：电源为38V/50Hz，系统阻抗为0.1Ω，进线电感为1mH；三相不可控整流桥带阻感负载，电感为2mH，电阻为10Ω；直流母线电压为80V，直流储能电容为5 000μF；系统频率为12.8kHz。

在检测设备和试验条件相同的情况下，用不同数字低通滤波器完成APF的谐波治理。原系统畸变率为24.04%；采用超前—滞后校正椭圆滤波器的APF治理后，系统畸变率为6%；采用超前校正椭圆滤波器的APF治理后，系统畸变率为6.9%；采用超前校正的巴特沃斯滤波器的APF治理后，系统畸变率为7.7%；采用滞后校正的椭圆滤波器的APF治理后，系统畸变率为7.2%。试验证明，数字滤波器的选取决定了谐波检测效果，且基于超前-滞后校正的椭圆数字滤波器优化设计的效果较好。

5　结束语

仿真结果和试验样机的实测结果表明，以二阶椭圆型数字滤波器为基础，加入超前-滞后校正对数字低通滤波器进行优化，使系统的动态性能更加优越，测量的准确性有所提高。单纯地加入超前校正，增加了系统的超调量；而只加入滞后校正，牺牲了系统的快速性。因此，基于超前-滞后校正对数字低通滤波器的优化，提高了谐波检测的准确性和实时性。在检测设备和试验条件相同的情况下，采用超前-滞后校正的优化数字低通滤波器，可以提高APF的性能指标，改善电网谐波的治理效果，从而证明了本文优化方法的合理性和有效性。此外，该方法易于数字实现，不需要额外的硬件投入，具有较高的实用价值。

[1] 周鹏,贺益康.电网电压不对称且谐波畸变时基波电压同步信号的检测[J].仪器仪表学报,2010,31(1):78-84.

[2] 周柯,罗安,夏向阳,等.一种改进的ip-iq谐波检测方法及数字低通滤波器的优化设计[J].中国电机工程学报,2007,27(34):96-101.

[3] 袁兆祥,郑建勇,胡敏强,等.有源滤波器中新型检测滤波器的设计[J].中国电机工程学报,2008,28(9):45-49.

[4] 陈仲.并联有源电力滤波器实用关键技术的研究[D].杭州:浙江大学,2005.

[5]KILICT,MILUNS,PETROVICG.Designandimplementationofpredictivefilteringsystemforcurrentreferencegenerationofactivepowerfilter[J].InternationalJournalofElectricalPower&EnergySystems,2007，29(2):106-112.

[6]CHUDAMANIR,VASUDEVANK,RAMALINGAMCS.Comparativeevaluationofharmonicextractiontechniquesforthree-phasethree-wireactivepowerfilter[C]//ProceedingsoftheInternationalConferenceonPowerElectronicsandDriveSystems.IEEE2007:1700-1706.

[7]BHATTACHARYAA,CHAKRABORTYA.Harmoniceliminationandreactivepowercompensationthroughashuntactivepowerfilterbytwinneuralnetworkswithpredictiveandadaptiveproperties[C]//IEEEInternationalConferenceonIndustrialTechnology，2009:1-6.

[8] 吴勇.有源电力滤波器若干关键技术研究[D].武汉:华中科技大学,2007.

[9] 史伟伟,蒋全,胡敏强,等.串联型电力有源滤波器中低通滤波器的设计及参数优化[J].中国电机工程学报,2001,21(11):74-78.

[10]王毅男,林伟.数字梯形成形滤波器的模块化设计[J].自动化仪表,2015,36(10):89-95.

[11]尚海涛,薛红喜.基于带通滤波器的ZoomFFT算法研究[J].自动化仪表,2011,32(4):11-17.

[12]洪露,沈记全,穆志纯.基于克隆选择调节算法的IIR数字滤波器设计[J].控制与决策,2007,22(11):1264-1268.

OptimizedDesignofDigitalFilterwithLead-lagCorrection

Aimingattheneedofharmonicdetectionofactivepowerfilter,anoptimizeddesignispresentedwithaddinglead-lagcorrectiontoimprovecharacteristicsoflow-passfilter.Second-orderellipsefilterischosenasthecoreoftheharmonicdetectionaftercomparingvariouskindsoffilters.Relationshipofparametersconfigurationwhichaffectssystemperformanceisworkedoutbyanalyzingdistributionofsystempole-zero,thenlead-lagcorrectionisaddedtooptimizelow-passfilter.Simulationandexperimentsshowthatthisoptimizeddesignbetterfitstherequirementsfordetectingthegridharmonicsandfundamentalreactivecurrent,makesthedetectionsystemmaysimultaneouslyobtainexcellentaccuracyandsatisfactorydynamicresponsespeed.

LeadcorrectionLagcorrectionHarmonicdetectionDigitallowpassfilterActivepowerfilterOptimization

郭喜峰(1981—),男，2013年毕业于东北大学电气工程专业，获博士学位，副教授；主要从事电能质量的研究。

TH7;TP2

ADOI:10.16086/j.cnki.issn1000-0380.201609022

国家自然科学基金资助项目(编号：51467017);沈阳建筑大学基金资助项目(编号：XKHY2-73)。

修改稿收到日期：2015-12-17。