高非线性光纤及超宽带波长转换器的研究

吴 迪，张 娜，游善红

（苏州大学a.电子信息学院；b.文正学院，江苏苏州 215006）

高非线性光纤及超宽带波长转换器的研究

吴 迪a，b，张 娜a，游善红a

（苏州大学a.电子信息学院；b.文正学院，江苏苏州 215006）

文章主要利用HNLF（高非线性光纤）实现超宽带波长转换。从HNLF出发，简单介绍了光纤的基本原理和参数，利用光纤的耦合振动方程，推导了FWM（四波混频）效应进行波长变换的理论依据，并分析了影响波长转换效率的因素。针对这些因素，利用Optisystem仿真软件在常规非线性光纤中进行仿真验证。通过调整相关参数，在自定义参数HNLF中实现了较大带宽和较高效率的波长转换。

波长转换；四波混频；高非线性光纤

0 引 言

随着光网络中信息流量的不断增长，因光频谱的重叠可能会造成阻塞和串扰。若在网络核心节点加入波长转换器，当发生波长冲突时将波长转换成空闲波长，可实现网络扩容、简化通信链路、节约频谱资源和减少干扰。利用光纤的非线性效应能够实现一定带宽内的波长转换。根据原理光纤的非线性效应可分为XGM（交叉增益调制）、XPM（交叉相位调制）和FWM（四波混频）等［1］。

利用FWM效应能够实现光波信号的完全透明传输，转换速率可达100Gbit/s，而HNLF（高非线性光纤）因非线性度高，能够有效缩短光纤长度。2001年华中科技大学基于XGM效应实现了波长间隔大于14nm，信噪比大于30dB的波长转换［2］，2008年北京大学同样基于XGM效应，实现了波长间距60nm、信噪比和消光比均大于10dB的波长转换［3］；而日本的古河光子学实验室（Fitel Photonics Laboratory）在2009年通过抑制受激布里渊散射获得了60nm宽的波长转换［4］。本文主要研究FWM下的波长转换。

1 四波混频原理

FWM起源于介质的束缚电子对电磁场的非线性响应［5］。由于二阶极化率通常为零，因此极化强度P展开到三阶时可以表示为

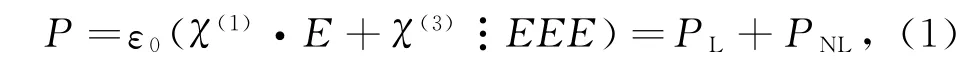
式中，E为电场强度；ε0为真空介电常数；χ（j）为第j阶极化率（通常是j+1阶张量）。χ（1）对P有主要的贡献，χ（2）在大多数分子对称的介质中都为零，因此一般光纤中的非线性最低是由三阶极化率导致的［6］。PL为P的线性分量，是带χ（1）的部分；PNL为P的非线性分量，是带χ（3）的部分。若假设存在4束角频率为ωi（i=1，2，3，4）的线偏振光沿同一x轴传播，则非线性部分可表示为

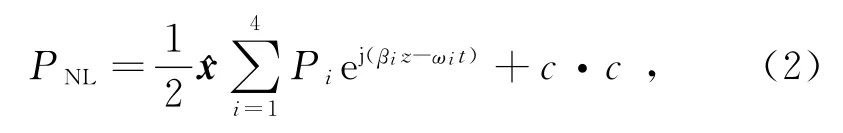
由此，对于θ-，若发生相位匹配，即ω1+ω2-ω3-ω4=0，则会产生新的频率ω4=ω1+ω2-ω3。如果将ω1与ω2简并，则有ω4=2ω1-ω3。一般情况下，我们将ω1和ω2作为泵浦光，ω3作为信号光，则ω4即为我们需要的转换光。

由上述分析可知，只有当相位失配几乎为零时才会发生明显的FWM。即必须满足。利用波动方程解耦合振动方程，可得4个频率的振幅［6-7］：

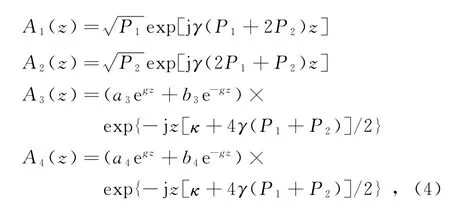
式中，Pi=|Ai（0）|2即为泵浦光的入射功率；γ为非线性系数（由于4束光波长差并不大，因此取4束光的平均非线性系数）；有效相位失配κ=Δβ+γ（P1+P2）；ai和bi是由边界条件确定的常数；参量增益g取决于泵浦功率，定义为

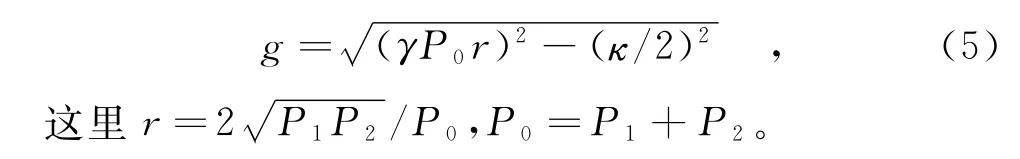
由此，可由转换光和信号光的功率比求得转换效率

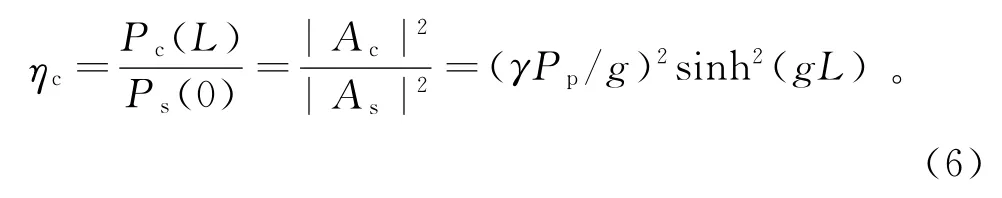
2 HNLF下的全光波长转换

目前全光波长转换按泵浦分类有三种方式：单泵浦、平行双泵浦和垂直双泵浦。下面通过Optisystem仿真软件来对上述理论推导进行验证。仿真所使用的光纤长度L=1km，零色散波长λ0=1 550nm，衰减α=0.5dB/km，色散D=1ps/（nm·km），色散斜率S=0.019ps/（nm2·km），有效面积Aeff= 2.6μm2，非线性折射率n2=2.6×10-20m2/W，非线性系数γ=4.05W-1/km。3种方式进行FWM的光路如图1所示［8］。

图1　3种FWM方案

2.1单泵浦情况

固定信号光功率，分别对功率为3、9和11dBm 的1 550nm泵浦进行仿真，可以发现随着泵浦功率的提升，转换光功率能够呈平方倍地提升。再固定泵浦光功率，将泵浦波长偏离零色散波长1 550nm，则转换效率会逐渐降低。最后固定泵浦功率、波长以及信号功率，仿真表明，单泵浦情况下的波长转换器是偏振敏感的，因为对于功率和波长都相同的信号光，随着其偏振态的变化，对应的转换光功率会发生显著的变化，而当信号光与泵浦光偏振正交时，转换光的功率趋向于0，即转换效率无穷小，这一结果显然是在实际应用中不愿意看到的。

在各条仿真曲线中，9dBm的泵浦光产生了大约4nm长的平坦转换带宽，如图2所示。这与实验中的带宽比较接近，对理论分析有一定的验证，但在实际应用中无法满足多信道同时转换的工作要求，只能应用在较为简单、信道数比较少的场合。

图2　单泵浦波长转换结果

2.2平行双泵浦情况

对于相位失配参数，引入两个泵浦的参数。定义两个泵浦之间的角频距离ωd=（ωp-ωq）/2，两个泵浦的中心频率ωm=（ωp+ωq）/2，由此可得

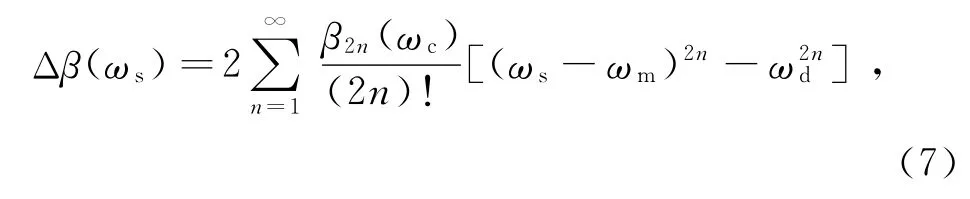
即转换光失配程度与两泵浦的间距和中心位置都有关系。由此，通过控制ωd同样可以控制相位失配，然后由此来补偿非线性相位失配γ（P1+P2），从而使有效相位失配κ在宽频谱范围内保持近似为零。

在仿真时，分别控制各变量，当仅泵浦功率发生变化时，其变化规律与简并时的结论一致；当控制两泵浦间距不变，改变泵浦的中心波长时，若中心频率接近零色散波长，则能够得到一条较宽的平坦带宽，随着中心频率偏离零色散波长，转换效率和平坦程度明显降低；而控制中心波长不变，拉开两泵浦的距离可以发现，当信号光与泵浦光较接近时，转换光的功率会有一个明显的提升，然后在零色散波长附近有一个极小值。虽然随着泵浦之间距离的拉开，能够得到相对平坦的带宽在增大，但是转换光功率在不断下降。在偏振态上，平行泵浦对一定范围内的信号的偏振态基本不敏感，因此可应用于高速偏振复用的传输系统。

由上述分析可知，平行泵浦情况下的转换光功率较单泵浦情况下有了一定的提高，但依然存在一些问题。在平行双泵浦下，我们能得到大约10nm的平坦转换带宽，如图3所示。

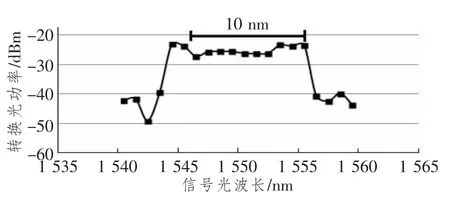
图3　平行双泵浦波长转换结果

2.3垂直双泵浦情况

由于两泵浦偏振态正交，引入琼斯矢量分析［8］。经过理论推导得到信号光和转换光的振幅分别为

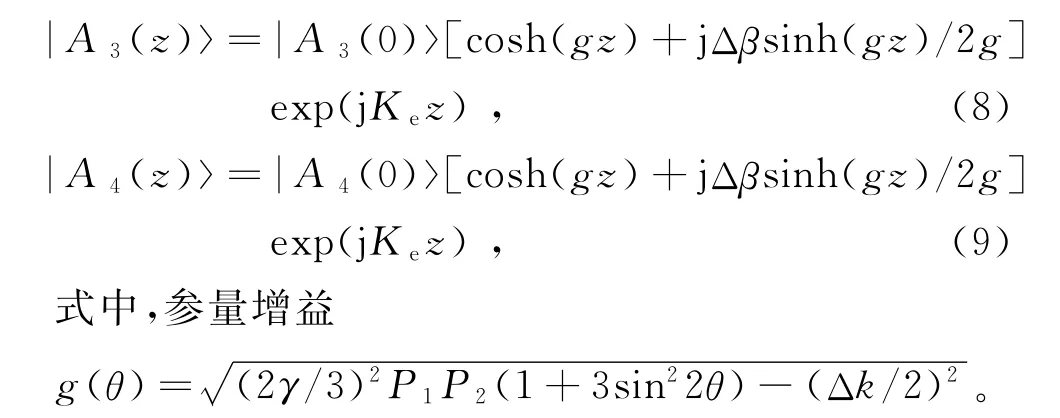
这里，θ为表征椭圆率的量，即当椭圆偏振成为圆偏振（θ=45°）时，参量增益达到最大。

垂直双泵浦情况下的相关结论与平行双泵浦基本一致。垂直双泵浦条件下双泵浦间的转换光功率比平行双泵浦的要小。但是在另一方面，垂直泵浦能够获得比平行泵浦更好的平坦带宽。最主要的是，垂直泵浦能够很好地克服信号光偏振态的变化而引起的转换效率的改变，这是单泵浦无法做到的。最终，在间距为1nm、中心波长（两个泵浦的平均频率所对应的波长）为1 550nm的垂直双泵浦下，我们得到了波长范围1 513～1 530nm内约17nm的平坦转换带宽，如图4所示。

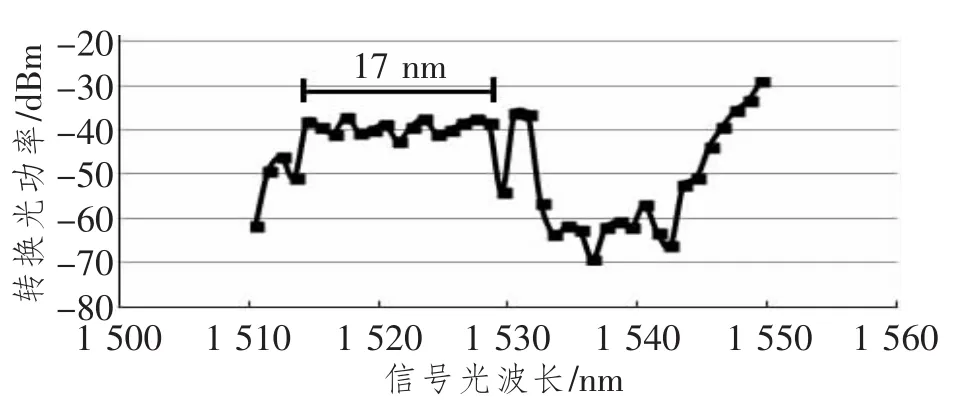
图4　垂直双泵浦波长转换结果

3 超宽带波长转换器的研究

在上面的分析中，我们大致得到了转换功率与泵浦功率、泵浦中心波长和泵浦间距的关系。接下来我们对不同非线性程度的光纤进行仿真。由于γ=2πn2/λAeff，其中n2是较难改变的，对纤芯是二氧化硅的材料n2=2.6×10-20m2/W。而通过调整纤芯半径a或参数V就可以调整Aeff。因此在1 550nm处附近，若Aeff在1～100μm2范围内变化，则γ会在100～1W-1/km范围内反比例变化［5］。可见，通过改变Aeff，就能获得HNLF。

通过仿真发现，随着光纤非线性程度的增加，转换光的功率在逐渐增加到一个峰值后又有一定的回落。由于在推导时忽略了XPM与SPM（自相位调制），且从参考文献［5］、［8］和［9］来看，SBS（受激布里渊散射）的阈值会随着模场面积的减小而减小，因此在缩小Aeff时，能量部分转移到了SBS上。在上面的仿真中，当γ达到30W-1/km时，转换平坦带宽约为15nm（1 527～1 542nm），转换功率在-35dBm左右。

而对β3进行分析可以发现，β3的大小对转换的功率影响不大。β3在0～15ps2/km范围内时，转换光的功率大致都在-40dBm附近。但不同取值的β3对稳定转换功率非常不同，带宽平坦度随着β3先升后降，在γ=25W-1/km时，若β3在5ps2/km附近，则转换光平坦度和平坦带宽最令人满意。

经过多次调整，以表1中参数设计了一条自定义参数的光纤，并进行了仿真。当信号光波长在1 510～1 540nm范围内时，可以得到-27dBm± 2dBm的平坦转换，带宽约为30nm，如图5所示。

表1　自定义光纤参数

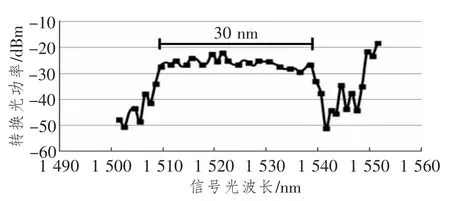
图5　自定义参数光纤波长转换结果

4 结束语

本文分析了单泵浦、平行双泵浦和垂直双泵浦情况下的FWM效果，并且着重分析了泵浦的功率、间距、中心频率以及信号的偏振态对转换光的影响，得出以下结论：第一，转换效率与泵浦的功率的平方成正比，但当泵浦功率超过一定阈值后，其他非线性效应将使转换效率快速衰落；第二，当泵浦的中心频率接近光纤零色散波长时，转换效率最高，而随着中心频率的偏离，转换效率逐渐降低；第三，泵浦的间距越大，则转换带宽越大，但转换效率会降低；第四，单泵浦对信号的偏振非常敏感，平行泵浦与垂直泵浦可实现对信号的偏振不敏感转换。最后，我们在理论上仿真得到了带宽范围约30nm的-27dB的超宽带平坦转换。

［1]贾光明，贾东方，李世忱.高非线性光纤及其应用［J］.光通信研究，2003，（1）：43-47.

［2]谢光，张新亮，龚威.基于交叉增益调制的全光波长转换实验研究［J］.光通信研究，2001，（3）：10-15.

［3]周黎，王子宇.基于SOA交叉增益调制的2.5Gbit/s NRZ码全光波长转换实验研究［J］.电子学报，2008，（4）：50-53.

［4]Takahashi M，Hiroishi J，Tadakuma M，et al.FWM wavelength conversion with over 60nm of 0dB conversion bandwidth by SBS-suppressed HNLF［C］// OFC 2009.San Diego，USA：OSA，2009：1-3.

［5]李淳飞.非线性光学［M］.第2版.北京：电子工业出版社，2010.

［6]Onishi M.Highly Nonlinear Dispersion-Shifted Fibers and Their Applications to Broadband Wavelength Converter［J］.Optical Fiber Technology，1998，（4）：204-214.

［7]Lu J.Polarization Insensitive Wavelength Conversion Based On Four-Wave Mixing For Polarization Multiplexing Signal In High-Nonlinear Fiber［J］.Optics Communications，2009，282：1274-1280.

［8]Agrawal Govind P.Nonlinear Fiber Optics，Fourth E-dition &Applications of Nonlinear Fiber Optics，Second Edition［M］.北京：电子工业出版社，2010.

［9]叶佩弦.非线性光学物理［M］.第1版.北京：北京大学出版社，2007.

Research on HNLF and Broadband Wavelength Converter

WU Dia，b，ZHANG Naa，YOU Shan-honga
（a.School of Electronic and Information Engineering； b.Wenzheng College，Soochow University，Suzhou 215006，China）

In this paper，we use a High Non-Linear Fiber（HNLF）to achieve broadband wavelength conversion.We first introduce the basic principles and parameters of HNLF，and then derive the theory of wavelength conversion based on Four-Wave Mixing（FWM）.Finally，the factors which may have influences on the conversion efficiency are analyzed.The simulations are conducted in the software Optisystem.After optimization of several parameters，we demonstrate a broadband and high-efficiency converter based on HNLF.

wavelength converter；FWM；HNLF

TN915

A

1005-8788（2016）02-0007-04

10.13756/j.gtxyj.2016.02.003

2015-11-19

吴迪（1992-），男，江苏南京人。硕士研究生，主要研究方向为光纤通信、数字图像处理。

游善红，副教授。E-mail：shyou@suda.edu.cn