电力牵引传动系统微秒级硬件在环实时仿真

郝 琦 葛兴来 宋文胜 冯晓云

（西南交通大学电气工程学院 成都 610031）

电力牵引传动系统微秒级硬件在环实时仿真

郝 琦 葛兴来 宋文胜 冯晓云

（西南交通大学电气工程学院 成都 610031）

为满足电力牵引传动系统高速实时仿真的需求，分析了交直交牵引传动系统的结构及其原理，建立了现场可编程门阵列硬件在环（HIL）仿真模型，其中包含单相脉冲整流器、中间直流回路、三相两电平逆变器以及异步电机四部分。对于含有开关器件的结构——逆变器和整流器，分别推导出它们不同状态下各自开关函数的逻辑表达式，考虑了变流器电流过零点时的换流情况。采用状态方程及矩阵方程分别对变流器以及异步电机进行建模，并将数学模型集成在FPGA中加以实现，在RT-LAB实时仿真器上进行HIL仿真，验证了仿真平台的正确性。由于采用FPGA模拟牵引传动系统，充分发挥了其善于并行计算的特性，大幅缩短了仿真的步长，突破了中央处理器速度限制，实现了微秒级系统模型实时仿真，提高了HIL仿真系统的响应速度以及准确度。

现场可编程逻辑阵列 微秒级 硬件在环 电力牵引传动系统 实时仿真 交直交

TM922

0 引言

近年来，在电力电子和电气传动领域，硬件在环（Hard-In-the-Loop, HIL）作为一种快速、安全和可靠验证控制器算法的途径逐渐得到了广泛应用[1]。开发过程中加入HIL仿真，可以提前测试系统的控制参数和算法，有效减少了研发的周期与成本[2]。在HIL仿真系统中，实时仿真器用数学模型模拟实际装置，实际控制器对其模型加以控制，二者进行数据交互，实现了系统多参数、多运行条件的测试，并具有灵活性好、体积小、周期短和准确度高等优点[3]。

文献[4,5]针对不同拓扑结构的电力牵引传动系统，建立实时仿真模型，仿真步长分别为 40μs和60μs，测试验证了模型的正确性。文献[6]为避免电力电子实时仿真模型求解发散，给出不同电路拓扑下能够保证模型求解收敛稳定的最大步长。文献[7]为了提高实时仿真准确度，研究了开关器件在相邻仿真时刻间动作时的补偿算法。无论是为了避免模型求解发散或是为了提高仿真准确度，缩小仿真步长都是最为直接有效的方法。

传统HIL仿真中，由中央处理器（CPU）承担模型解算工作，由于其模拟程序采用串行计算方式，速度难以进一步提升，HIL仿真步长通常在 10μs数量级[8]。较高的仿真步长意味着低采样速率，为了精确体现控制器脉冲控制效果，只能通过额外器件精确抓取脉冲变化时间，在下一个仿真周期中引入算法加以补偿。如若强制缩短仿真步长，又会导致计算超时，进而引起仿真数值的不稳定。HIL系统中负责数据交互的模-数、数-模器件频率动辄上兆赫兹，控制器——FPGA或 DSP，其控制周期也能达到10μs这一数量级。显然，实时仿真器的速度已经成为仿真系统的瓶颈，影响了实时仿真速度进一步提升。

目前为止，FPGA凭借其高时钟频率、高可靠性和多输入、输出等特点，承担了电力电子装置驱动脉冲发生工作，应用已非常普遍[9-11]。在 HIL仿真方面，FPGA主要应用在硬件接口中，承担仿真器与控制器间信号交换[12]。但是，FPGA还具备潜力替代CPU成为电力电子系统的仿真运算单元。文献[13]分析了电力电子器件的开关特性和换流过程，并在FPGA中实现其实时仿真，在器件级的水平上反映出开关过程中电压、电流尖峰及功率损耗等关键指标。文献[14]针对两电平电压源型逆变器及异步电机进行建模，采用FPGA对系统模型进行仿真，仿真步长为10μs，实现了对电机的矢量控制HIL实时仿真。

本文以交直交电力牵引传动系统为对象，提供了一种高速实时仿真的建模和实现方法，完成了牵引传动系统1μs步长的HIL仿真。基于硬件描述语言（Hardware Description Language，HDL）在FPGA中实现了电力牵引传动系统主电路拓扑建模以及牵引异步电机建模，构建了电力牵引交流传动系统HIL仿真平台，并完成了实时仿真模型HIL仿真测试。与传统基于CPU的实时仿真系统相比，仿真步长大幅减小，仿真模型动态响应速度提高，此外还避免CPU模型解算中复杂的时间补偿算法，提高了仿真准确度。

1 电力牵引传动系统HIL仿真简介

电力牵引传动系统包括牵引变压器、单相脉冲整流器、中间直流回路、三相两电平逆变器和牵引异步电机[15]。牵引变压器将单相 50Hz工频交流降压，供给单相整流器，后者将交流电变为直流电，并通过中间直流回路输送给逆变器。逆变器将直流电变换为频率幅值可变的三相交流电，驱动牵引异步电机，为整个系统提供动力[16]。

图1给出了电力牵引传动系统HIL仿真框图。与传统实时仿真相比，将被控对象的模型由CPU中转移到FPGA芯片中进行计算。采用双DSP分别作为整流器系统和逆变器电机系统的控制器。脉冲整流器系统控制算法采用瞬态电流控制，调制算法采用SPWM。逆变器电机系统控制算法采用转子磁场定向间接矢量控制，调制算法采用 SVPWM，其中低速区为异步调制，中高速区为分段同步调制。

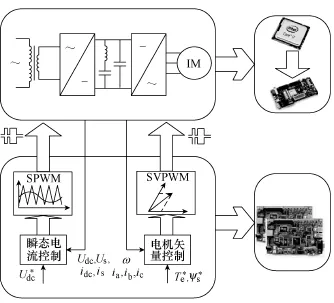
图1　电力牵引传动系统HIL仿真框图Fig.1 HIL of electrical traction drive system

2 牵引变流器建模

Matlab/Simulink、PSCAD等仿真软件在求解电路时，根据其拓扑和参数将待求电路化为高阶方程组，并进行求解，其中涉及到行列式变换、矩阵乘法求逆等，这类复杂运算在FPGA上实现较为困难。为满足实时仿真系统的高速性，本文采用状态方程对变流器进行建模，忽略器件导通时的电阻和关断时的电导，便于牵引变流器模型的求解。将整流器、逆变器以及连接二者的直流电路视为变流器的三个核心部分，进行统一建模。整流器、逆变器共同完成了交直交传动系统的电能变换，中间直流回路作为两者能量传输的桥梁。

2.1单相脉冲整流器及直流环节模型

牵引变压器将供电系统的电能变换电压等级，变压器一次侧、二次侧电动势同频率、同相位，仅幅值不同。为降低仿真系统的复杂度，建模时只考虑变压器二次侧，将其等效为正弦交流电源与变压器二次侧漏电感Ls和绕组电阻Rs串联，如图2所示。

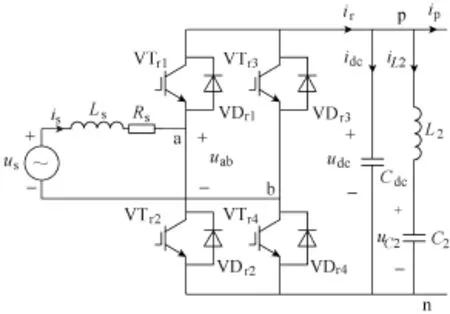
图2　单相整流器及直流环节电路结构Fig.2 Topology of the single-phase rectifier and DC-link circuit

单相整流器由a桥和b桥两个桥臂组成，每个桥臂包含两个IGBT和两个二极管，共同组成一个全控桥电路。建立整流器理想开关函数，描述a桥、b桥导通关断，其开关函数Sra、Srb状态可定义为

则整流器输出电流和输入端电压可以分别用开关函数表示为

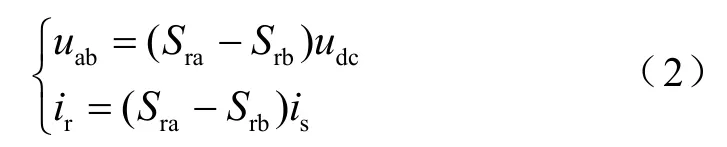
式中，udc为直流侧电压；uab为整流器输入端电压；is为变压器二次电流；ir为整流器输出电流。

中间直流回路包含一个直流电容器 Cdc和一个包含电感L2和电容C2的LC滤波电路，后者的谐振频率设置为100Hz。

至此，将整流器、变压器与中间直流回路联合起来，图2所示的电路拓扑数学模型可以描述为

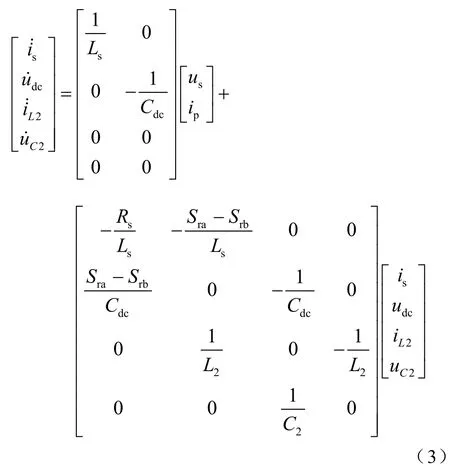
式中，Cdc为直流侧电容；C2为滤波电路电容；L2为滤波电路电感；us为变压器二次电压；uab为整流器输入端电压；uC2为电容 C2电压；iL2为电感 L2电流；ip为直流电路输出电流。

2.2牵引逆变器模型

逆变器主电路如图3所示，它由三相桥臂u、v 和w组成，每个桥臂有两个IGBT以及与其反并联的二极管构成，共同构成三相电压源型逆变器。

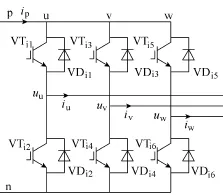
图3　三相两电平逆变器电路拓扑Fig.3 Topology of the three-phase two-level inverter

与整流器类似，用开关函数描述逆变器开通关断状态，即

在牵引传动系统中，逆变器向电机提供三相交流电压。取直流侧支撑电容中点为零电位点，则电机三相输入电压及直流回路输出电流可以描述为

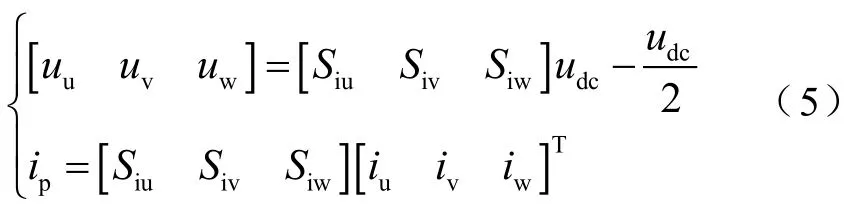
式中，uu、uv和uw分别为电机u、v和w三相输入电压；iu、iv和iw分别为电机u、v和w三相电流。

2.3FPGA实现

对于整流器和逆变器，开关函数取值由其接收控制器的触发脉冲所决定。

以整流器为例，整流器拓扑包含四个开关管，开关管信号组合有24=16种，其中有七种信号组合会引起直流母线短路，排除后仍有九种，而开关函数Sra与Srb组合仅有22=4种，开关函数与触发脉冲存在一定的映射关系。因此，首先要确定如何根据触发脉冲来获得开关函数。

变压器漏电感的续流作用会维持变压器二次电流 is方向不变，而电流流向的不同也会影响桥臂导通关断状态。枚举出 is为任意方向时，不同触发脉冲组合对应的开关函数，表1给出了具体开关函数取值。

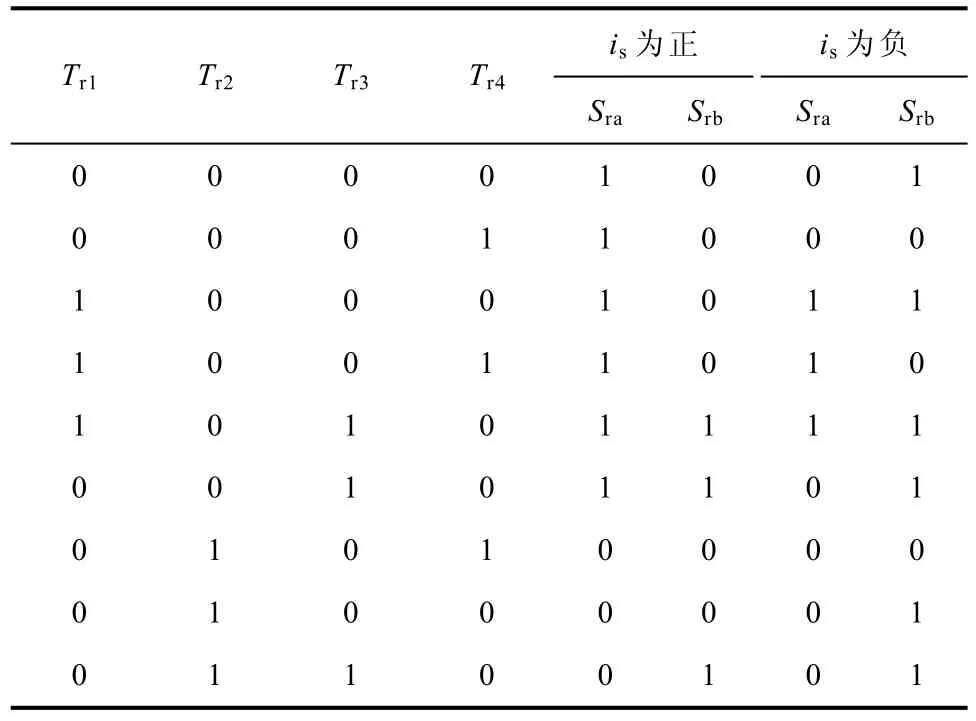
表1　触发信号与开关函数对照Tab.1 Corresponding rules between trigger signal and switching function

当is大小接近于0时，电感续流作用可被忽略，此时开关器件通断情况受交流侧电压以及直流侧电压影响。定义阈值δ，当时，不再以is正负来判断开关函数取值，类似地，列举出不同电压条件下的开关函数的值，文中不再给出。实际情况中，δ 取值视系统功率等级和模型计算步长不同而变化，功率等级越大或计算步长越大，对应δ 取值越大，此处取0.5Α。

若采用C语言实现，为得到不同情况下开关函数取值，需要加入一系列条件判断语句。而对FPGA来说，实现条件判断效率并不高，需要耗费较多的硬件资源。

电流方向、电压正负和电压间大小比较都可化为二进制 01变量，IGBT的触发脉冲也用01变量表示。而FPGA恰好善于组合逻辑运算，因此，本文考虑用逻辑表达式来表示 Sra和 Srb，并利用卡诺图化简逻辑函数得

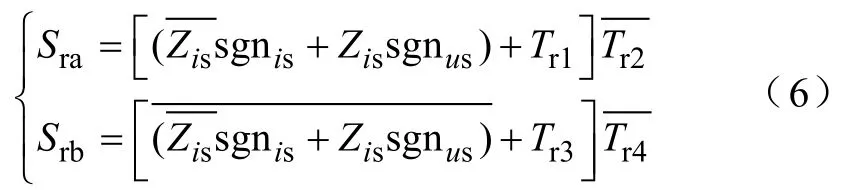
式中，Zis、sgnis和sgnus分别对应电感电流过0判断、电感电流方向和网侧电压正负三个逻辑变量。

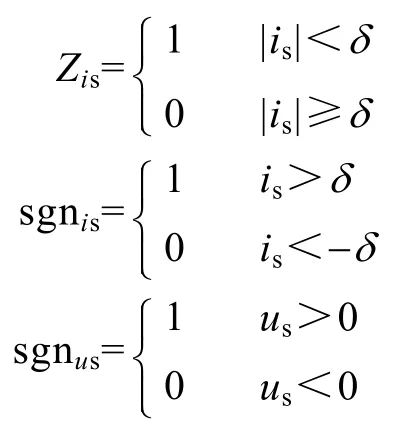
此外，当电感不具备续流作用时，整流器还存在一种特殊的工作情况。例如：当 udc＞us＞0、|is|＜δ 时，Tr2=Tr3=0，Tr1、Tr4不同为1。此时，由于Tr1、Tr4并没有同时接收导通触发脉冲，对于is来讲，只存在顺时针导通的回路（流经二极管），而不存在逆时针导通的回路（流经IGBT），并且由于udc＞us，二极管承受反向压降，无法导通。在FPGA实现过程中，驱动is寄存器的复位信号使之为0。

对于逆变器，由于电机的定子绕组也呈感性，同样具有续流作用。定义电机电流方向逻辑变量为

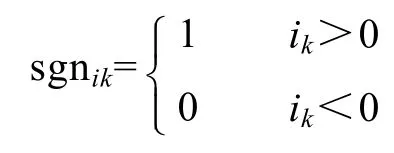
式中，k可取u，v和w。

电机与中间直流环节不同，不存在电容维持电机侧电压，因此不必考虑电机电流过0点时的桥臂导通情况。

同样，利用卡诺图对其进行化简得到逻辑函数

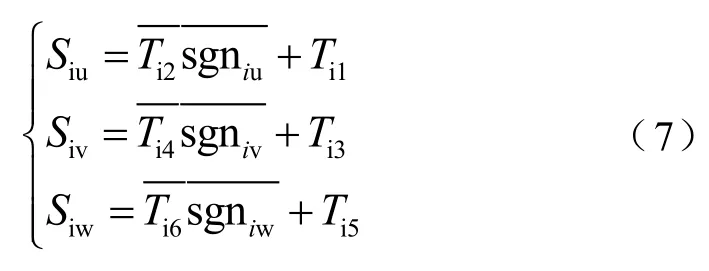
为保证模型求解速度，模型中变量、参数统一以定点数参与运算，表2中给出了牵引变流器模型中变量定点数表示。以交流电压 us的定点数精度16.8为例，用16个二进制位表示电压的整数部分，8个二进制位表示电压的小数部分。

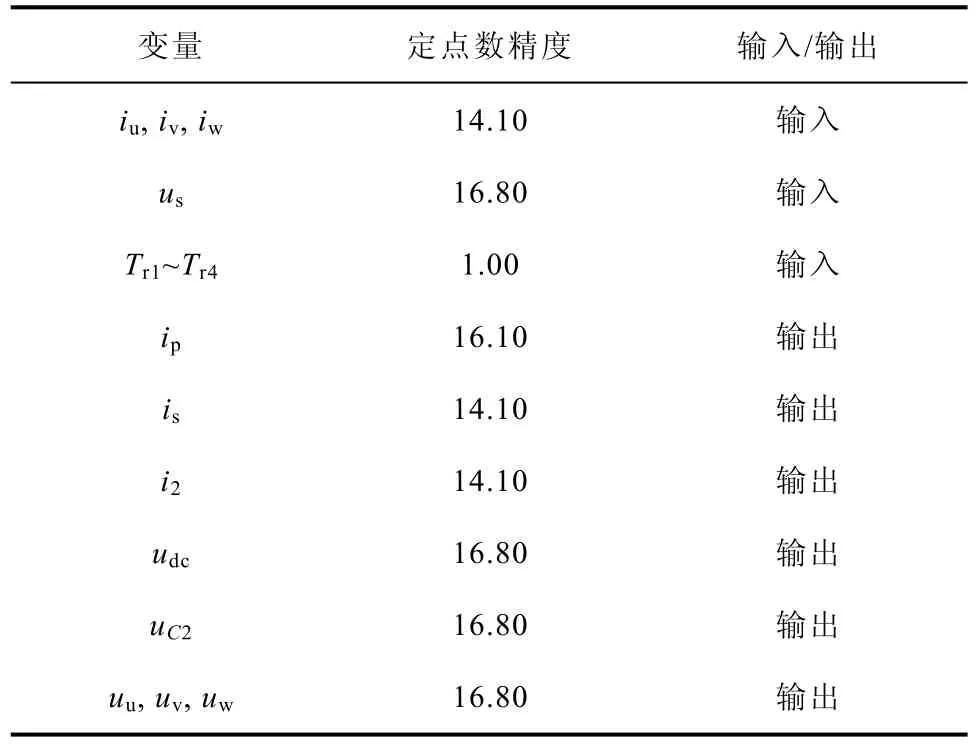
表2　牵引变流器变量定点数表示Tab.2 Fix-point format of variables in traction converter

本文中，采用了梯形公式对状态方程进行积分计算。由于将模型集成在FPGA中，使得模型求解步长大幅度缩短，梯形公式积分已经可以满足较高的仿真准确度。

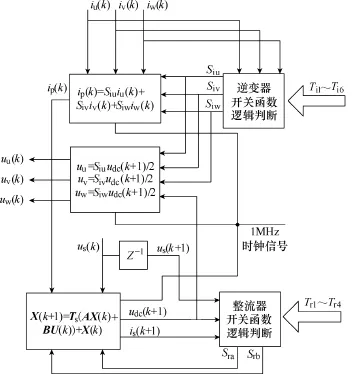
图4 牵引变流器模型离散化框图Fig.4 The block diagram of discretization modeling of a traction converter

图4中给出了变流器模型的离散化具体实现框图，其中，Ts为 FPGA模型仿真步长，为1μs。由于模型中，式（3）相对较为复杂，用状态方程一般形式进行表示。

最后，FPGA实现过程中也考虑了短路故障情况，当监测到整流器或逆变器上下桥臂同时接收到导通信号时，模型会向上位机发送短路报警信号。

3 异步电机建模

电力牵引传动系统通常选取三相异步电机，将电能转化为机械能，为列车提供行驶动力。三相异步电机本身是一个高阶非线性的多变量系统，本文采用静止αβ坐标系下异步电机模型对其建模。

3.1牵引异步电机模型

首先，将牵引变流器的输出三相电压uu、uv和uw采用矢量合成方式，转换为两相静止αβ坐标系下的电压uαs、uβs为

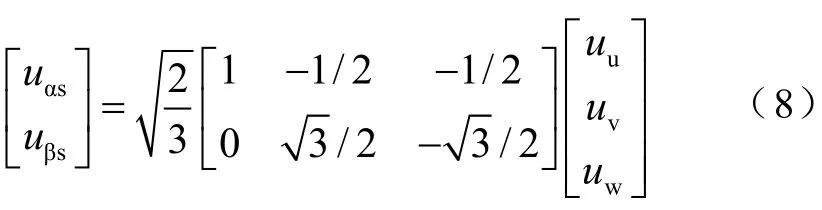
因此，在两相静止坐标系下，异步电机的状态方程模型如式（9）～式（13）所示。

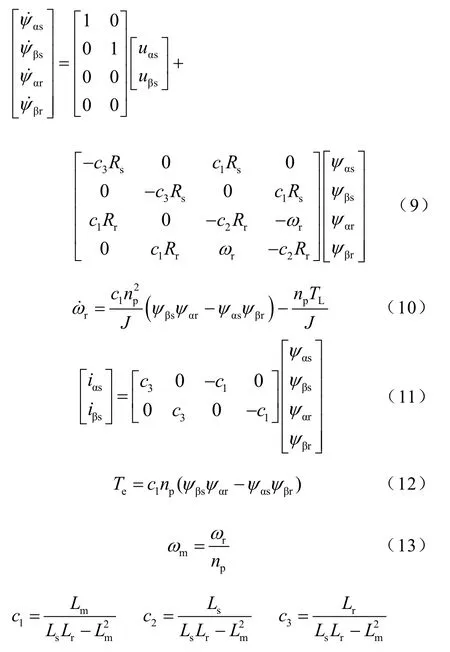
式中，Rs为定子内阻；Rr为转子内阻；Lm为互感；Ls为定子自感；Lr为转子自感；ψαs、ψβs为定子磁链在α轴和β轴分量；ψαr、ψβr为转子磁链在α轴和β轴分量；uαs、uβs为定子电压在α轴和β轴分量；iαs、iβs为定子电压在α轴和β轴分量；np为级对数；ωr为转子电角速度；ωm为转子机械角速度；J为转动惯量；Te为电磁转矩；TL为负载转矩。

最后，将两相静止坐标系下的电流iαs、iβs转换为三相交流电流iu、iv和iw，转换公式为

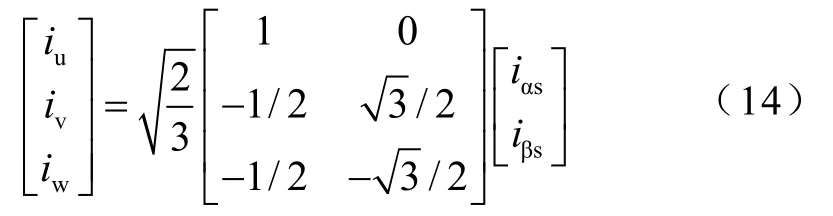
式中，iu、iv、iw作为电机输出，同时作为逆变器的输入反馈回变流器模型。

3.2FPGA实现

在FPGA实现过程中，主要是对模型的离散化处理。图5给出了异步电机模型的离散化具体实现框图，Ts为FPGA模型仿真步长，为 1μs。由于式（9）相对较为复杂，用状态方程一般形式X= AX+BU进行表示。

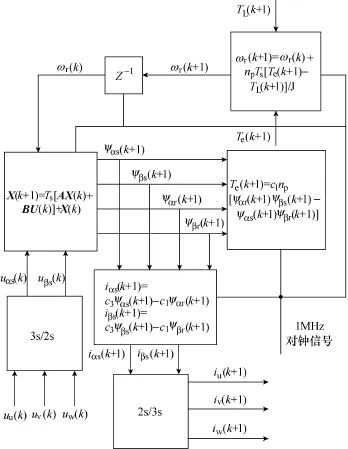
图5　异步电机模型离散化框图Fig.5 The block diagram of discretization modeling of an induction motor

在该模型中，四阶状态方程以转子和定子磁链为状态变量，描述电机电磁特性，一阶状态方程以转子电角速度ωr为状态变量，描述电机机械特性。由于转速相对磁链来说是慢变量，ωr(k)与ωr(k+1)的角速度变化差值相对较小。因此，先由ωr(k)作为初值计算第k+1时刻转子和定子磁链，再由磁链计算第k+1时刻Te和ωr。

表3给出了异步电机模型中变量定点数表示。

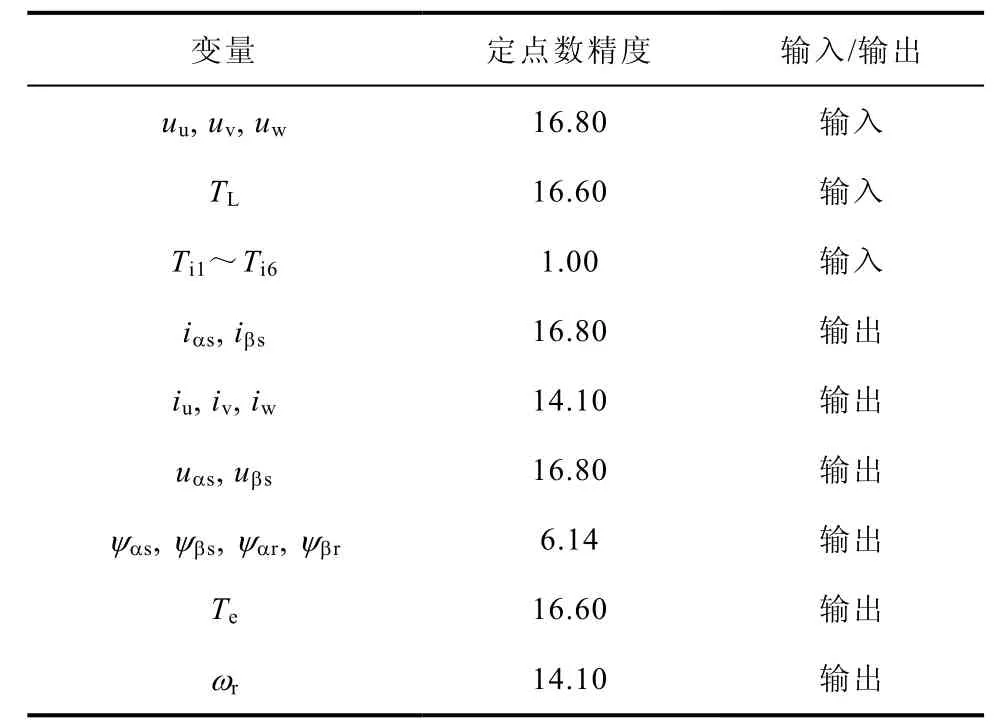
表3　异步电机变量定点数表示Tab.3 Fix-point format of variables in an induction motor

表4给出了模型各部分调用基本运算模块的数量。加法运算、移位和多路选择均可以在一个时钟周期完成，乘法运算相对复杂，采用流水线乘法器加以实现，对于一个N位数乘法器需要INT(log2N)级加法实现。模型中的乘数均不超过32位，考虑到移位及其他操作的时间，乘法运算耗时共6个时钟周期。FPGA芯片时钟频率为 100MHz，乘法运算时间为60ns，其他运算操作则需10ns，对表4各部分求和，共 750ns。此外，模型中需对关键变量添加寄存器，保证数值稳定，通过控制器脉冲计算得到变流器开关函数，亦需要计算时间。故考虑时间裕量将 100个 FPGA时钟周期设为仿真步长，即1μs，各计算模块受1MHz的信号触发，信号占空比为1%，保证了每1μs系统完成一次完整运算。

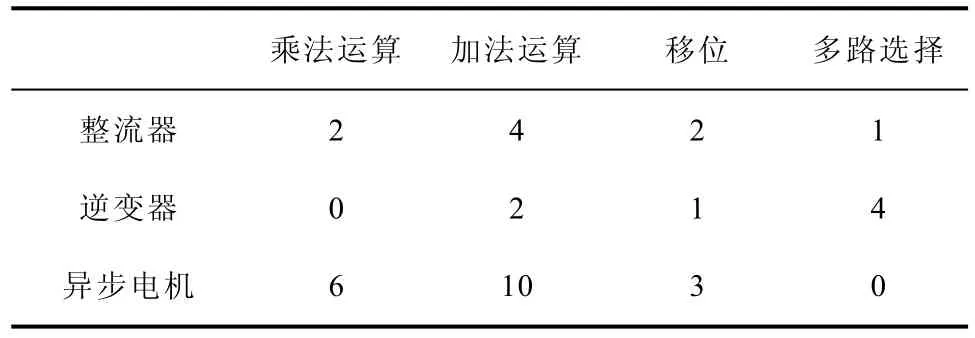
表4　模型各部分运算模块使用数量Tab.4 Numbers of operation modules of each part in this model

本文采用了Xilinx公司的System Generator系统级工具箱对整个电力牵引传动系统模型进行实现。该工具箱提供了图形化的设计界面，并且提供了Matlab/Simulink的接口。

4 HIL仿真验证

4.1HIL仿真平台框架

图6a和图6b分别给出了HIL仿真平台的框架结构示意图和实物图。上位机与RT-LAB仿真器通过以太网线通信，上位机可观测模型中的变量，并可配置模型参数。RT-LAB实时仿真器包含两个运算单元：CPU为Intel Core-i7处理器，FPGA为Xilinx Virtex-6芯片。CPU将配置信号通过PCI-E总线发送给FPGA，并接收来自FPGA的待观测量。FPGA还负责与数字、模拟板卡通信的工作，模型中的电流、电压、转速和转矩等信号经过模拟板卡OP5330输出。其中电压、电流信号发送给 DSP的模-数模块。电机的转速信号，经过正交编码脉冲（Quadrature Encoder Pulse，QEP）电路，通过OP5354数字输出板卡发送至DSP的QEP模块，FPGA通过数字输入板卡OP5353，接收来自DSP的PWM信号，控制模型中虚拟的整流器和逆变器。值得一提的是，OP5353、OP5354和 OP5330中的所有信号都可以在RT-LAB仿真器I/O面板通过示波器进行观测。牵引控制单元（TCU）由TI公司TMS320F2812为核心的器件构成。

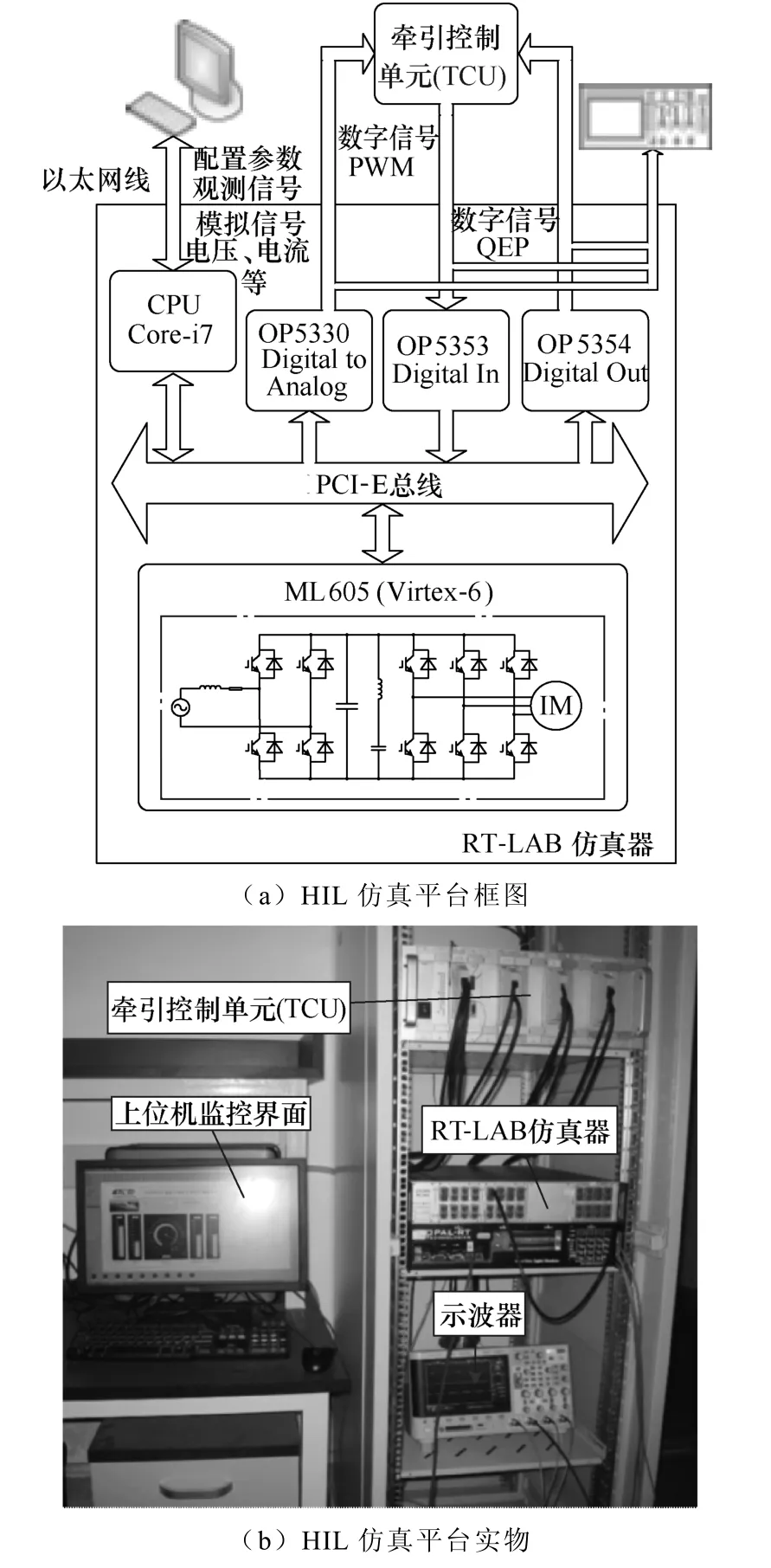
图6　电力牵引传动系统HIL仿真平台Fig.6 The block diagram and photo of hardware-in-the-loop simulation platform for electrical traction drive systems

4.2测试结果

为了验证所建模型的正确性和适用性，基于图6所示的HIL仿真平台，对电力牵引传动的FPGA模型进行测试。具体系统参数配置见表 5。其中，逆变器要同时驱动四台异步电机，脉冲整流器系统控制算法采用瞬态电流控制，调制算法采用SPWM。逆变器电机系统控制算法采用转子磁场定向间接矢量控制，调制算法采用 SVPWM，低速区为异步调制，中高速区为分段同步调制。

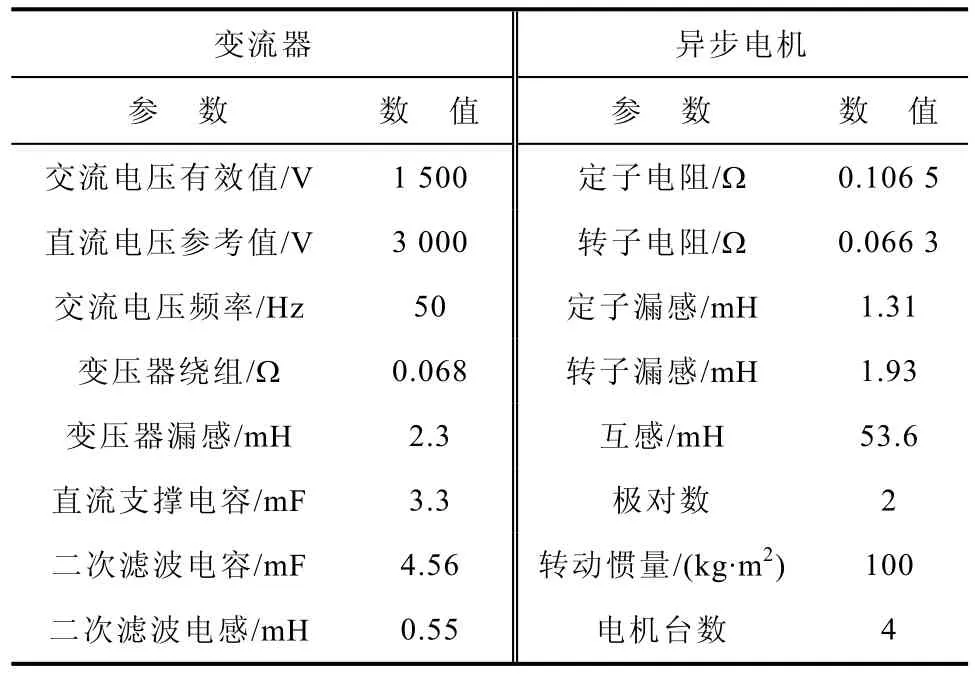
表5　电力牵引传动系统HIL仿真参数Tab.5 The HIL simulation parameters of an electrical drive system

图7所示为单相整流器模型工作在不控整流状态时网侧电压、电流仿真波形。以网侧电压 us＞0时为例说明：t＜t1时，udc＞us，二极管反向阻断，整流器 a、b两桥臂均未导通，is=0；t1＜t＜t2时，udc＜us，二极管VDr1、VDr4正向导通，整流器a桥上桥臂和b桥下桥臂导通，Ls正向充电，is增大；t2时刻，udc=us，is增至最大值，由于Ls续流作用，维持 VDr1、VDr4导通；t2＜t＜t3时，udc＞us，Ls持续放电，is减小；t3时刻，is减小为0，a、b两桥臂变为关断状态。

图8给出整流器在瞬态电流控制下，电压与电流波形。由图8可知，网侧电流is正弦度高，与交流电压us同频同相位，整流器工作在单位功率因数下。ip为直流侧输出电流。

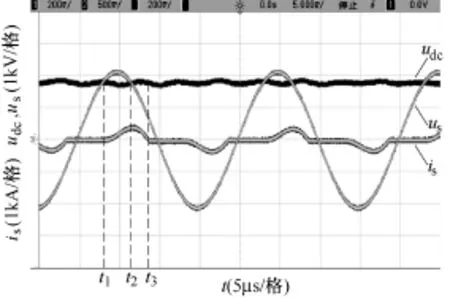
图7　不控整流网侧电压与电流仿真波形Fig.7 Simulation waveforms of the main voltage and the line current in diode-rectification mode

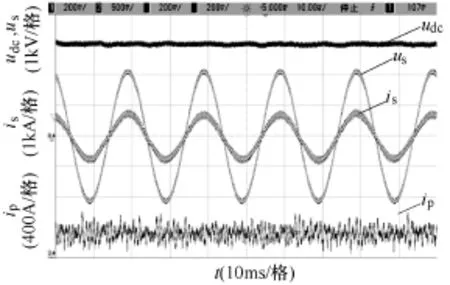
图8　瞬态电流控制下整流器网侧和直流侧电压与电流波形Fig.8 Simulation waveforms voltage and current of AC side and DC side of rectifiers with transient current control

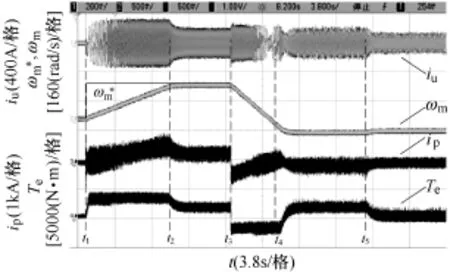
图9 异步电机矢量控制全过程的定子电流、转速、直流侧电流和转矩仿真波形Fig.9 Simulation waveforms of stator current, speed, DC-link current and torque of the asynchronous motor with vector control in the whole operations process

图9给出了异步电机起动运行全过程的定子电流、转矩、直流侧电流和转矩波形，其中给定转子磁链ψs*=5Wb。t1时刻，给定转速ωm*=200rad/s，电机带载起动，输出转矩给定值 Te=3 000N·m，负载转矩 TL=1 500N·m，电机匀加速起动，相电流 iu起动时电流幅值保持不变，频率增大，电机输入电流ip线性增加，能量由直流侧传导至电机侧。t2时刻，电机达给定转速，输出转矩Te=TL=1 500N·m。t3时刻，给定转速改变为ωm*=−50rad/s，输出转矩给定值Te=−2 000N·m，ωm匀减速变化，ip突变为负值并呈上升趋势变化。t4时刻，ωm达给定转速，电机反转，能量由电机侧反馈回直流环节，ip由正变为负并保持相对稳定。t5时刻，TL变为0，Te迅速变为0，电机转差也变为0，电机转速有略微上升。

在电力牵引传动系统中，受变流器体积及散热器散热能力限制，除异步调制外，往往在较高频率范围，引入分段同步调制、方波控制，在保证不超过发热量限制值的前提下，降低电流谐波含量、抑制转矩脉动。

图10中给出了不同调制模式下，各过程的牵引电机三相电流波形。调制模式切换时，三相定子电流过渡平稳，证明了FPGA电机模型在各种调制模式下都能正确稳定工作。

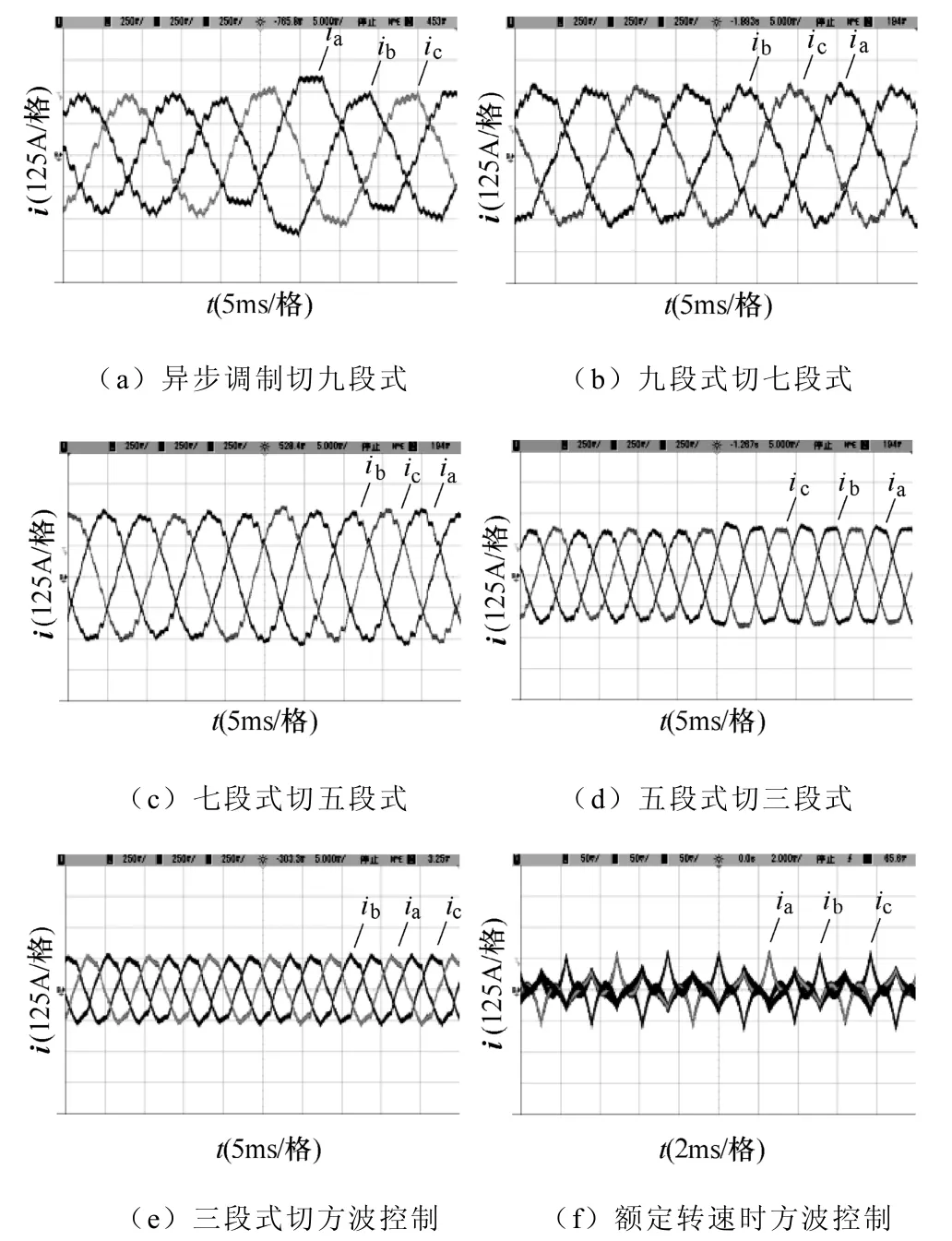
图10 不同调制模式过程中三相定子电流波形Fig.10 Simulation waveforms of three-phase stator current under different module modes

图11对比不同实时仿真中CPU模型和FPGA模型整流器交流侧电流的变化情况，说明FPGA模型运算速度上的优势。图11a中，CPU模型运算步长为20μs，电流is呈阶梯状变化。对于开关信号Tr3、Tr4的窄脉冲，由于模型计算的延迟，is并未对其作出响应，继续增大。图11b中，FPGA模型运算步长为1 μs，电流连续性更高。对于开关信号Tr3、Tr4的窄脉冲，is立即响应变化。FPGA模型相对于传统CPU模型提高了仿真计算速度。

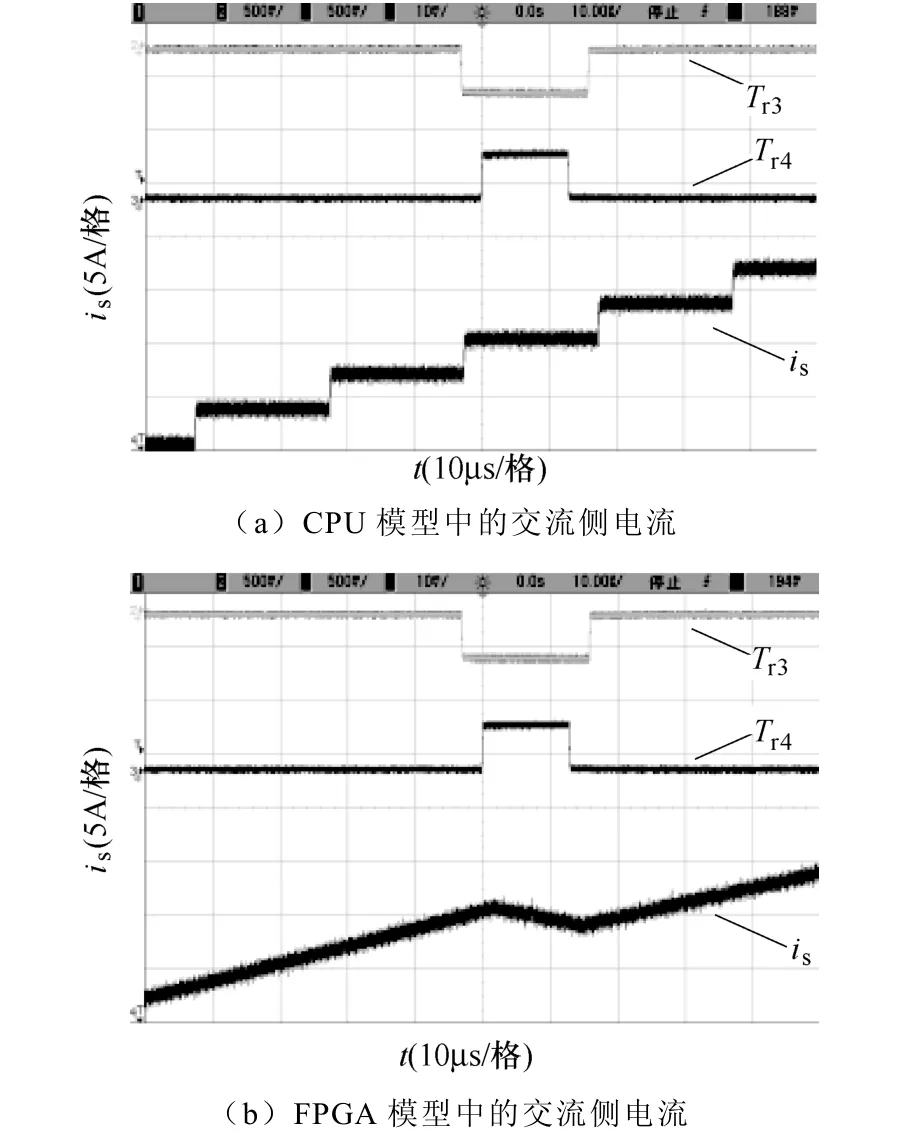
图11　电力牵引传动系统的CPU模型与FPGA模型对比Fig.11 The comparison between CPU model and FPGA model of an electrical traction drive system

5 结论

本文以提升电力牵引传动系统实时仿真速度为目标，分析了系统的结构和原理，推导了开关逻辑函数，充分考虑了变流器过零点换流情况，并采用状态方程对牵引传动系统中的变流器及异步电机进行建模。通过System Generator工具将模型集成在FPGA芯片中，由于其高速并行的计算特性，实时仿真步长仅为1μs，相较于基于CPU的实时仿真，速度提高了一个数量级，避免了复杂的时间补偿算法。实验证明模型的正确性、可靠性。1μs的实时仿真步长提高了HIL仿真动态性能和仿真准确度，降低了计算带来的延迟。

本文对电力牵引传动系统的建模方法具有普遍性。本文所构建的模型包含了电阻、电感和电容等构成电路的基本元件，单相及三相变换器，以及非线性的异步电机模型。建模思路和方法具有一定的借鉴和推广价值。

[1] Pak L F, Faruque M O, Nie X, et al. A versatile cluster-based real-time digital simulator for power engineering research[J]. IEEE Transactions on Power Systems, 2006, 21(2): 455-465.

[2] 何舜, 张建文, 蔡旭. 风电变流器的 RT-LAB硬件在环仿真系统设计与实现[J]. 电力系统保护与控制, 2013, 41(23): 43-48. He Shun, Zhang Jianwen, Cai Xu. Realization and design of wind power converter model based on RT-LAB HIL system[J]. Power System Protection and Control, 2013, 41(23): 43-48.

[3] 李秋硕, 张剑, 肖湘宁, 等. 基于 RTDS 的机电电磁暂态混合实时仿真及其在 FACTS中的应用[J].电工技术学报, 2012, 27(3): 219-226. Li Qiushuo, Zhang Jian, Xiao Xiangning, et al. Electromechanical-electromagnetic transient realtime simulation based on RTDS and its application to FACTS[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 219-226.

[4] 丁荣军, 桂卫华, 陈高华. 电力机车交流传动系统的半实物实时仿真[J]. 中国铁道科学, 2008, 29(4): 96-102. Ding Rongjun, Gui Weihua, Chen Gaohua. HIL realtime simulation of electric locomotive AC drive system[J]. China Railway Science, 2008, 29(4): 96-102.

[5] 葛兴来, 宋文胜, 冯晓云. 基于 dSPACE的高速列车牵引传动系统[J]. 电力自动化设备, 2012, 32(3): 18-22. Ge Xinglai, Song Wensheng, Feng Xiaoyun. Drive system based on dSPACE platform for high-speed train[J]. Electric Power Automation Equipment, 2012, 32(3): 18-22.

[6] Jin H. Behavior-mode simulation of power electronic circuits[J]. IEEE Transactions on Power Electronics, 1997, 12(3): 443-452.

[7] Kuffel P, Kent K, Irwin G. The implementation and effectiveness of linear interpolation within digital simulation[J]. International Journal of Electrical Power & Energy Systems, 1997, 19(4): 221-227.

[8] 郭希铮, 游小杰, 徐从谦, 等. 大功率电力牵引控制系统硬件在回路实时仿真[J]. 电工技术学报, 2012, 27(4): 65-70.Guo Xizheng, You Xiaojie, Xu Congqian, et al. Simulation of hardware in loop for high-power electrical traction system[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 65-70.

[9] 邱大强, 李群湛, 舒泽亮, 等. 基于 FPGA 的综合潮流控制器的设计与实现[J]. 电力系统保护与控制, 2010, 38(24): 163-167. Qiu Daqiang, Li Qunzhan, Shu Zeliang, et al. Design and realization of integrated power flow controller based on FPGA[J]. Power System Protection and Control, 2010, 38(24): 163-167.

[10] 罗德荣, 王耀南, 葛照强, 等. 级联型高压变频器控制算法的研究及实现[J]. 电工技术学报, 2010, 25(1): 104-110. Luo Derong, Wang Yaonan, Ge Zhaoqiang, et al. Research and realization of control algorithm of cascaded high voltage converter[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 104-来110.

[11] 赵耀, 赵庚申, 郭天勇, 等. 基于 SVPWM 低谐波死区算法的研究及应用[J]. 电力系统保护与控制, 2012, 40(8): 57-62. Zhao Yao, Zhao Gengshen, Guo Tianyong, et al. Research and application of low harmonics dead-time injection based on SVPWM[J]. Power System Protection and Control, 2012, 40(8): 57-62.

[12] 傅成骏. 轨道交通车辆交流传动系统硬件在回路仿真技术进展[J]. 机车电传动, 2009(3): 1-4. Fu Chengjun. Development of hardware-in-loop simulation technology for AC drive systems in rail vehicles[J]. Electric Drive for Locomotives, 2009(3): 1-4.

[13] 马晓军, 杨宗民, 刘春光, 等. 电力电子器件的实时仿真[J]. 电力系统自动化, 2013, 37(18): 108-112. Ma Xiaojun, Yang Zongmin, Liu Chunguang, et al. Real-time simulation of power electronic devices[J]. Automation of Electric Power Systems, 2013, 37(18): 108-112.

[14] Parma G G, Dinavahi V. Real-time digital hardware simulation of power electronics and drives[J]. IEEE Transactions on Power Delivery, 2007, 22(2): 1235-1246.

[15] 冯晓云. 电力牵引交流传动及其控制系统[M]. 北京: 高等教育出版社, 2009.

[16] 宋文胜, 冯晓云, 侯黎明, 等. 电力牵引传动系统的三电平直接转矩控制算法的半实物实验研究[J].电工技术学报, 2012, 27(2): 165-172. Song Wensheng, Feng Xiaoyun, Hou Liming, et al. Hardware-in-loop research of three-level direct torque control scheme for electric traction drive system[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 165-172.

Microsecond Hardware-in-the-Loop Real-Time Simulation of Electrical Traction Drive System

Hao Qi Ge Xinglai Song Wensheng Feng Xiaoyun
（School of Electrical Engineering Southwest Jiaotong University Chengdu 610031 China）

The structure and principle of electric traction drive system are analyzed, and a field-programmable gate array (FPGA) model is built for hardware-in-the-loop (HIL) simulation, to meet the demand of real-time high speed simulation. This model consists of a single-phase rectifier, the DC-link circuit, a three-phase two-level inverter and asynchronous motors. For the inverter and rectifier which include switching devices, logical expression functions are derived under different switching states. State equations and matrix equations are applied in modeling converters and asynchronous motors respectively. In addition, the mathematical model is integrated into the FPGA chip. The test on HIL simulation in the RT-LAB real-time simulator has verified this FPGA model. As a result, the simulation step decreases sharply, breaking the speed limit of general-purpose processor. The real-time HIL simulation method at microsecond level improves the response speed and accuracy of the electrical traction drive system modeling.

Field-programmable gate array, microsecond, hard-in-the-loop, electric traction drive system, real-time simulation, AC-DC-AC

郝 琦 男，1991年生，硕士研究生，研究方向为电力牵引交流传动及其控制。

E-mail: curiouse@gmail.com

葛兴来 男，1979年生，博士，副教授，研究方向为电力牵引系统控制及其故障检测与诊断技术。

E-mail: xlgee@163.com（通信作者）

国家自然科学基金——高铁联合基金重点项目（U1134205）和国家自然科学基金（51207131、51277153）资助。

2014-02-21 改稿日期 2014-07-08