基于模糊专家系统的输电线路分段冰风荷载等效停运率模型

段 杰 王秀丽 侯雨伸

（西安交通大学电气工程学院 西安 710049）

基于模糊专家系统的输电线路分段冰风荷载等效停运率模型

段 杰 王秀丽 侯雨伸

（西安交通大学电气工程学院 西安 710049）

输电线路通常跨度较大，针对一条输电线路在同一时间不同区段可能处于不同冰冻风险等级的状况，引入串联网络模型，先对线路分段，考虑外界条件对停运率的影响，然后再整合，得到整条线路的等效停运率。考虑到气象预测误差和电力系统运行的不确定性对线路停运率计算的影响，建立基于模糊专家系统的线路非解析可靠性模型，将分段等效模型中停运率与主要外界影响因素之间的确定性关系模糊化，选择合适的模糊集、隶属度函数和模糊规则来弥补预测数据不准确带来的缺陷。以IEEE RBTS系统为例，预先设定线路各段所处的天气状况、地形状况和系统运行状态，求解特定工况下线路条件相依的综合停运率。计算结果表明，分段等效模型能够更加准确、合理地反映天气状况和系统状态的变化对线路综合停运率的影响，为评估线路运行风险和电力系统运行可靠性提供了基础。

线路停运率 分段模型 模糊专家系统 风力荷载 冰力荷载

0 引言

2008年发生在我国南方大范围的低温雨雪冰冻灾害使我国南方多个地区的电力设施损坏严重，电力供应遭到严重破坏，电力线路冰闪跳闸，电力杆塔断线倒塔等，对经济和社会活动造成的直接经济损失达到 1 500亿元，电网在这次极端天气条件下的脆弱情况令人大为震惊。事实上，由于过去冰灾的出现次数和影响范围较小，加之以往电力设施建设远没有现在密集，冰冻灾害造成的损失并没有引起人们的足够重视。近年来随着电网规模不断扩大和延伸，冰冻和暴（雨）雪等灾害性天气对电网安全运行的影响也越来越大，因此积极开展极端冰冻灾害对电网安全运行影响的可靠性评估显得非常迫切和重要[1-3]。

从以往事故的统计数据来看，在恶劣天气条件下，空气温度、风速和湿度等环境条件及负荷电流等运行条件以及电力设备的服役时间等不断变化使得电力系统元件的短期可靠性不断改变，继而影响了系统的运行可靠性水平。其中，覆冰引起的冰力荷载和风向、风速引起的风力荷载对线路故障的影响非常显著，当气温＜0℃持续时，电气设备产生覆冰并持续增长，与此同时，受线路覆冰的影响，线路等效半径明显增大，对线路承受的风力荷载影响显著，两者共同作用导致大量的线路故障停运。另外，输电线路上的潮流变化对停运率的影响同样是一个重要因素，因为潮流越限引起的温升使其机械强度缺失，导线被拉长。而导线被拉长后不可避免地引起下垂，接头处融化，从而增加闪络的风险[4]。

建立条件相依的线路短期停运率模型是运行可靠性评估的基础。如果电力系统可靠性评估过程中不考虑恶劣天气条件对电力系统的影响，评估结果会偏乐观，这将影响电力系统的规划和设计。目前已有较多文献对极端天气条件下电力系统的运行和风险进行了研究，但是主要集中在研究覆冰机理和增长模型、线路监测以及融冰技术策略[5,6]等。文献[7]基于瞬时状态概率采用快速排序算法评估了发输电系统的短期可靠性。这些研究都采用恒定的元件故障率，没有考虑天气环境和电气量等运行条件对元件停运的影响，难以反映运行条件的变化对系统短期可靠性的影响。文献[8-10]介绍了与天气条件相依的电网可靠性评估方法，但都以同一线路受到单一气象条件影响为前提，并没有考虑到同一线路不同地段气象条件的差异性所导致的电网风险差异。文献[11]分析故障率对电网设计的危险性时主要基于元件故障率的长期统计值，并未考虑某些地区缺少原始数据记录的问题，因此即使建立了线路可靠性的模型也很难确定相应的参数。文献[12]通过模糊规则系统建立了元件停运模型，是一种较合理的处理方法，但其仍是按照整条线路受单一天气条件作用的思路来考虑三种不同影响因素对停运率的综合作用，而且其不同因素对停运率的影响简单取最大值来计算，也忽视了冰力和风力荷载的联合作用。

针对以上问题，本文研究了分段冰风荷载等效停运率模型。针对一条输电线路在同一时间不同区段可能处于不同冰冻风险等级的状况，引入串联网络模型，对线路分段考虑外界条件对停运率的影响，然后再整合得到整条线路的等效停运率。考虑到气象预测误差和电力系统运行的不确定性对线路停运率计算的影响，建立了基于模糊专家系统的线路非解析可靠性模型，将分段等效模型中停运率与影响因素之间的确定性关系模糊化，选择合适的模糊集、隶属度函数和模糊规则来弥补预测数据不准确带来的缺陷。此方法建立的线路短期停运率模型是运行可靠性评估的基础，可以为运行决策和线路设计提供参考。

1 停运率影响因素数学模型

冰力荷载、风力荷载和线路的潮流水平是影响输电线路停运率最重要的因素[13]。线路荷载和停运率之间的关系，可以用表达式λ=f (loadice)和λ= f (loadwind)表示，但目前国内外对此都没有确定的数学表达式。瑞典研究人员根据现场和统计经验得到了线路停运率与风力荷载和冰力荷载的离散表达式[5]。鉴于国内目前还没有针对荷载值的停运率统计数据，故本文引用瑞典统计数据并在此基础上修改后进行分析。

1.1冰力荷载

线路上的冰力荷载是一个积累的过程，影响覆冰的因素包括温度、湿度和风速等，这里简单给出在满足温度和湿度条件下冰力荷载的计算，即覆冰现象已经出现的冰力荷载计算方法。详细计算步骤见文献[14]。

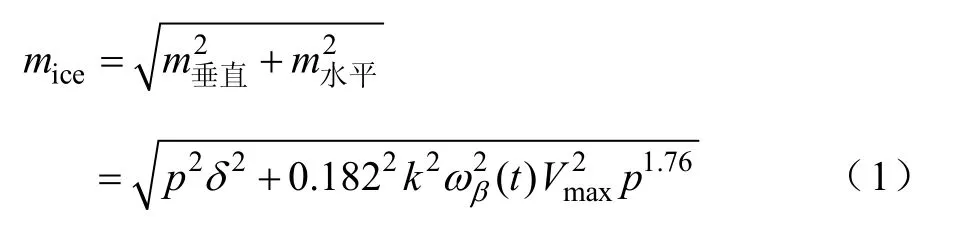
撞击到线路上的雨雪总质量为式中，p为降雨速率（mm/h）；δ 为水密度（g/cm3）；ωβ(t)为夹角因子, ωβ(t)=sinβ(t)，β (t)为风向和导线之间的夹角，是锐角；k为地形对风速的影响因子；Vmax为气象局发布的地区最大风速（m/s）。

设冰冻天气持续时间为t，单位是h。第i小时的降雨率和风速预测风别为pi和Vi，则第t小时导线冰力荷载为

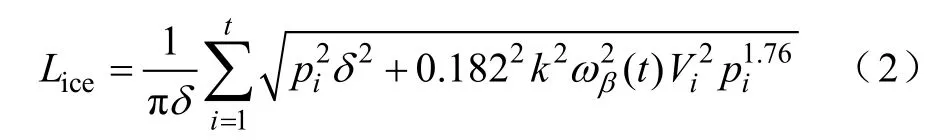
将冰力荷载对线路破坏作用的严重程度分为三个等级：极端恶劣、恶劣和正常状态。由瑞典统计数据加以改造得到冰力荷载三个等级与线路停运率之间的统计关系见表1。

表1　冰力荷载与线路停运率关系Tab.1 Relationship between failure rate and ice load

1.2风力荷载

线路上的风力荷载大小与距风场中心的距离和风场强度有关，风力可以由风场强度系数AF、到风场中心点的距离r以及气候影响因子表示。在冰冻天气中，导线上的覆冰随时间的推移而加剧，导线的等效半径会发生变化，风对导线的作用力也发生变化，因此在风力荷载的计算中应该考虑覆冰引起导线半径增大对风力荷载的影响。输电线路上的风力荷载为

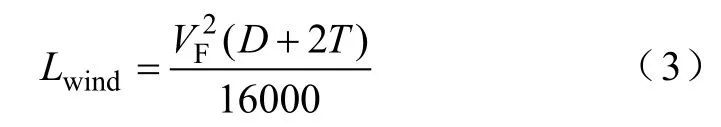
式中，D为导线直径（mm）；T为覆冰厚度（mm）。VF计算式为

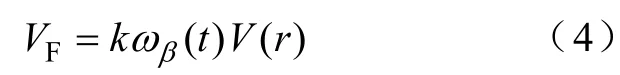
式中，k和ωβ与冰力荷载计算式公用，V(r)计算式为

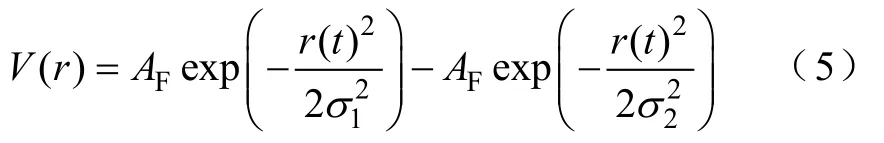
式中，r(t)≤R，R为风场影响半径（km）；AF为风场强度系数（m/s），对应风速指标；σ1、σ2为气候影响因子，其值与气候半径有关。

与冰力荷载对输电线路的影响作用相似，将风力荷载对线路破坏作用的严重程度分为三个等级。由瑞典统计数据加以整理得到风力荷载三个等级与线路停运率之间的统计关系见表2，其中为风力荷载的设计值。

表2　风力荷载与线路停运率关系Tab.2 Relationship between wind load and failure rate

1.3线路潮流

输电线路过载会导致线路的停运，本文将线路潮流水平对线路破坏作用的严重程度分为两个等级：正常和恶劣状态。假设线路潮流水平的额定值为 ID，线路潮流水平在 110%ID以下时，其停运率较低，为正常状态；当过载水平超过110%ID时，其停运率迅速增大，为恶劣状态。潮流水平与线路停运率之间的关系见表3。

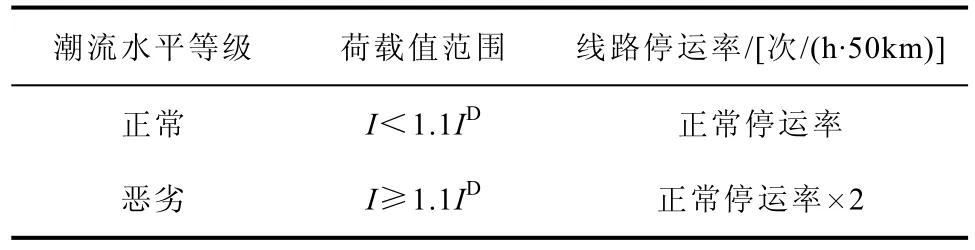
表3　潮流水平与线路停运率关系Tab.3 Relationship betwwen power flow and failure rate

2 线路分段等效模型

当采用均一的气象模型时，一条输电线路只有一个修复率和一个停运率。而对于跨度较大的输电线路，可能遇到不同级别的冰冻灾害，造成一条输电线路不同区段覆冰严重程度差异很大。本文采用分段模拟反映输电线路各区段处于不同的气候条件时，其停运率、修复率以及故障概率均不同。假设冰冻灾害严重程度近似认为一条线路跨越了N个不同的气候区，从逻辑上看，输电线路可模拟成由 N个不同故障率元件串联的等效元件[4,15]，如图1所示。

图1　线路分段等效模型Fig.1 The segmented equivalent model of transmission line

将一条输电线路分为N段，每一段占线路总长的百分数为 ki，其自身停运率为λi，则每一段等效停运率为kiλi。串联网络等效停运率为

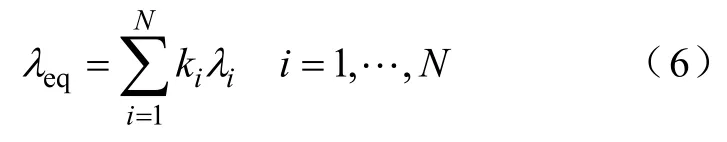
串联网络等值可用率为

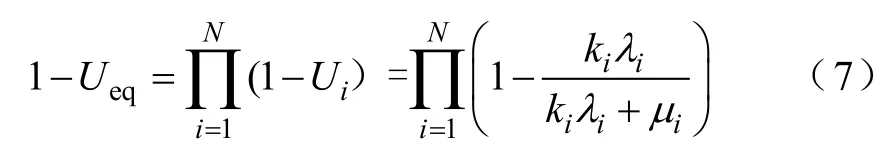
式中，Ueq为网络等效不可用率；Ui为元件不可用率；μi为元件修复率。

冰冻灾害对电网的影响主要是通过覆冰和风力两因素的综合作用完成的。当冰力荷载和风力荷载共同影响线路停运率时，其内部联系可通过两者的可靠性模型表示[13]，表现在停运率上可以表示为

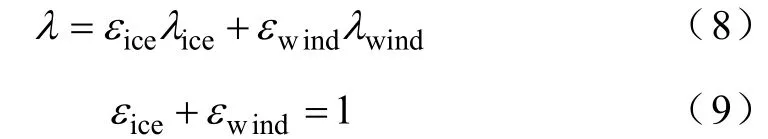
式中，λice、λwind分别为风力、覆冰导致的设备停运率；εice、εwind分别为对应的权重系数，一般通过经验获取，在本文中取εice=0.7、εwind=0.3。

3 线路分段等效模型模糊化

采用上述分段模型求线路的综合停运率并不准确，主要原因有两个：①气象预测的不确定性和微地形对区域覆冰的影响导致冰冻灾害的实际影响范围判定具有模糊性；②在实际运行中没有充分的数据确定线路过载水平与停运率之间的对应关系，即与潮流水平相对应的线路停运率没有精确值。在统计数据缺失的情况下，这两个问题可以利用模糊建模较好地解决。模糊理论已经在电力系统中得到了广泛的应用，其通过将专家经验和模糊数学相结合，把隶属度函数的概念引入专家系统的模糊知识中，能够克服传统专家系统处理问题过程中出现的许多概括性的、笼统的自然语言以及具有不完善之处的专家经验知识模型，从而实现快速准确的模糊推理[16,17]。

由上述可知，输电线路停运率模糊建模的三个影响因素为冰力荷载、风力荷载和线路潮流水平。冰力荷载和风力荷载的综合作用通过式（8）加以整合。在模糊建模上，冰力荷载影响和风力荷载影响相似，由于篇幅限制，本文仅通过将受冰力荷载影响的线路分段等效模型模糊化加以阐释。

3.1模糊输入变量隶属度函数

定义模糊语言变量 Xice-worst表示极端恶劣气象条件在线路上的影响范围，取值范围为[0,1]，最严重的情况下整条线路处于极端恶劣气候条件，取值为 1；最好的情况下整条线路处于正常气候条件，取值为 0。其模糊词集为{≤A1；约 A2；约 A3；约A4；≥A5}，本文取{≤0.2；约0.35；约0.5；约0.65；≥0.8}，是电网运行人员根据经验得出的典型影响范围数值。SA1、SA2、SA3、SA4、SA5和 SA6为各停运率值对应的极端恶劣气象条件影响范围的输入隶属度函数，如图2所示。

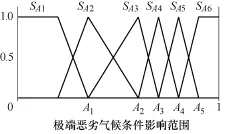
图2　Xice-worst隶属度函数Fig.2 Membership function of Xice-worst

其中影响范围SA4的三角形模糊输入函数为

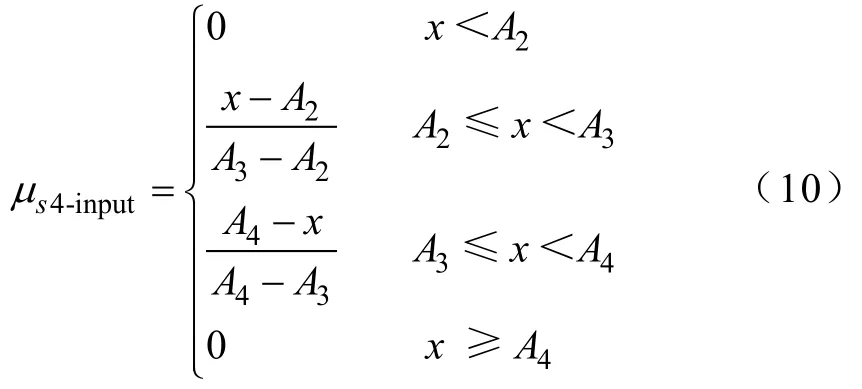
采用同样的方法可以建立恶劣气象条件影响范围Xice-medium的三角形模糊输入函数。其模糊词集为{≤B1；约B2；约B3；约B4；≥B5}。本文为了简单，同样取词集为{≤0.2；约0.35；约0.5；约0.65；≥0.8}。SB1、SB2、SB3、SB4、SB5和 SB6为各停运率值对应的恶劣气象条件影响范围的输入隶属度函数。

由于极端恶劣气象条件、恶劣气象条件和正常气象条件的影响范围相加之和应为线路总长度 1，因此正常气象条件的影响范围不作为一个输入变量，在计算过程中只要前两者确定下来，正常等级气象条件的影响范围也随之确定。

定义模糊语言XFlow表征输电线路的过载水平，其隶属度函数如图3所示，模糊词集中只有一个元素 I。本文取 ID为线路潮流额定值，假设线路潮流水平在1.1ID以下时，其停运率为正常停运率；当过载水平超过1.1ID时，其停运率增加为原停运率的2倍。SC1和SC2为各停运率对应的线路潮流水平输入隶属度函数。

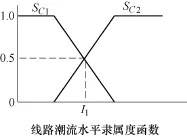
图3　XFlow隶属度函数Fig.3 Membership function of XFlow

3.2模糊输出隶属函数

根据三角形模糊输入变量的隶属度函数，定义三角形模糊输出变量隶属度函数。如由 SA4、SB2和SC2三个输入状态决定的模糊输出隶属度函数，其区域为[fmin, fmax]，上、下限分别是当线路有A5、A3长度处于极端恶劣气候区域、B2、B3长度处于恶劣气候区域且线路潮流水平超过1.1ID时，由分段模型计算得到的线路综合停运率。最大隶属度停运率 fmid为当线路A4范围处于极端恶劣气候区域、B2范围处于恶劣气候区域且线路潮流水平超过额定值时，由分段模型计算得到的线路综合停运率。其他各模糊输出隶属度函数可类似求得。

3.3if-then模糊推理规则

根据线路冰力荷载输入变量状态的划分，按影响范围建立极端恶劣等级六个隶属函数、恶劣等级六个隶属函数和潮流水平两个隶属函数，共 72个if-then模糊推理规则。

规则 1：当线路处于极端恶劣气候条件的部分为0，处于恶劣气候条件的部分为0，线路潮流水平为“≤额定值的 110%”，整条线路停运率约为4.5×10−3次/(h·50km)

…

规则24：当线路处于极端恶劣气候条件的部分为50%，处于恶劣气候条件的部分为35%，线路潮流水平为“＞额定值的110%”，整条线路停运率约为(0.07×0.5+0.03×0.35+4.5×10−3×0.15)×2次/ (h·50km)=0.092次/(h·50km)

…

规则72：当线路处于极端恶劣气候条件的部分为100%，处于恶劣气候条件的部分为0，线路潮流水平为“＞额定值的110%”，整条线路停运率约为0.07×2次/(h·50km)=0.14次/(h·50km)

3.4模糊推理算法

采用多规则、多输入和单输出if-then模糊推理模型，规则数为72，三个模糊输入变量分别为极端恶劣等级影响范围、恶劣等级影响范围和线路潮流水平，模糊输出变量为线路停运率。模糊推理算法采用 Mandani算法，推理合成规则为极大-极小运算。输入变量权重系数为 1，合成方法为求和，解模糊方法采用中心平均加权解模糊化方法[18]。

4 算例分析

本文以IEEE RBTS为算例，选取其中线路L2（120km）处于冰冻灾害天气。设冰冻天气持续时间为7h，风力影响半径R为60km，冰力影响半径也为 50km，风力气候的移动速度为 90km/h，线路与风力移动方向的夹角为 45°，线路冰力荷载设计值为15mm，风力荷载设计值为1.2kg/m，σ1=0.4R，σ2= 0.05R。值得指明的是，在一般情况下，风力气象中心和冰雪气象中心并不在同一点上，因此对线路的影响范围有所不同。考虑冰力荷载作用时，外界环境对线路 L3的影响使 L3形成三个不同的气象区。其中，a段线路降雪率为p1，b段线路降雪率为p2，两地降雪率见表4，c段线路受冰冻灾害非常轻，设其冰力荷载一直处于额定荷载范围内。

表4　不同区域降雪率预测Tab.4 Snowfall forecast in different regions

考虑风力荷载作用时，外界环境对线路L3的影响也使L3形成三个不同的气象区。其中，d段线路途经山谷地区，并且距离风力气象中心的距离较近，风力荷载对线路的影响最大；e段线路途经山谷地区，但是距离风力气象中心的距离较远，因此风力荷载的影响作用较d段有减弱，但仍然处于恶劣等级下；f段线路离风力中心的距离过远，风力作用对其影响很小，设其风力荷载一直处于额定荷载的范围内。

通过风力荷载和冰力荷载模型可以计算出各地段各时段的线路风力和冰力荷载值。因为篇幅原因，具体计算过程略去。线路各区间段冰力荷载和风力荷载随时间变化的曲线如图4所示。

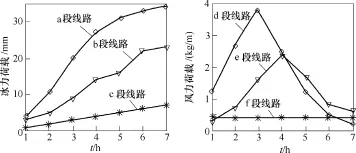
图4　冰力荷载和风力荷载随时间变化Fig.4 The ice load and wind load changing with time

从图4可以看出，线路所受的冰力荷载和风力荷载随气象中心的移动而发生变化，其中线路上的冰力荷载是一个随时间累积的积分过程，随时间推移其值不断增大；风力荷载与风力气象中心的移动方向有较大关系，风力方向与线路段的夹角越小，风力荷载越小，距离风力气象中心的距离越近，线路风力荷载越大；随着风力气象中心的不断移近再移远，风力荷载值呈先增大后减小趋势。

当t=5h时，线路地理布局与所处气候条件的示意图如图 5所示。a、b、c三段冰力荷载的预测值分别为27mm、16.5mm和5mm，所占整条输电线路的长度比分别为0.46、0.28和0.26。通过把冰力荷载计算值与设计值拟合对比，得到线路该时段的分段停运率。a、b、c三段线路所对应的线路停运率分别为 0.04次/(h·50km)、0.03次/(h·50km)、4.5×10−3次/(h·50km)。由于风力气象中心和冰雪气象中心不在同一点，用 d、e、f三段线路表示同一时刻风力荷载对线路停运率的影响。此时三段线路风力荷载的预测值分别为 1.7kg/m、1.2kg/m 和0.4kg/m，所占整条输电线路长度比分别为0.4、0.4 和0.2，把风力荷载计算值与设计值对比，得到对应的线路停运率分别为4×10−2次/(h·50km)、5×10−3次/ (h·50km)、8×10−4次/(h·50km)。

设定线路潮流水平为额定值的 102%。将线路分段模型模糊化，针对风力荷载对线路停运率的影响，模糊输入变量为极端恶劣气象条件影响范围、恶劣气象条件影响范围和线路潮流水平，三者输入值分别为0.46、0.28和1.02时，真正起作用的模糊规则有八项，见表5。输入变量权重系数为1，合成方法为求和。采用Mandani模糊推理算法，推理合成规则为极大-极小运算。

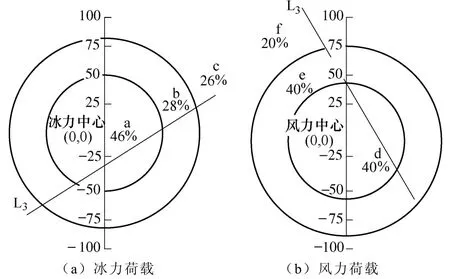
图5　冰力、风力荷载单独影响时的线路地理布局Fig.5 The transmission line geographic distribution influenced by ice and wind respectively

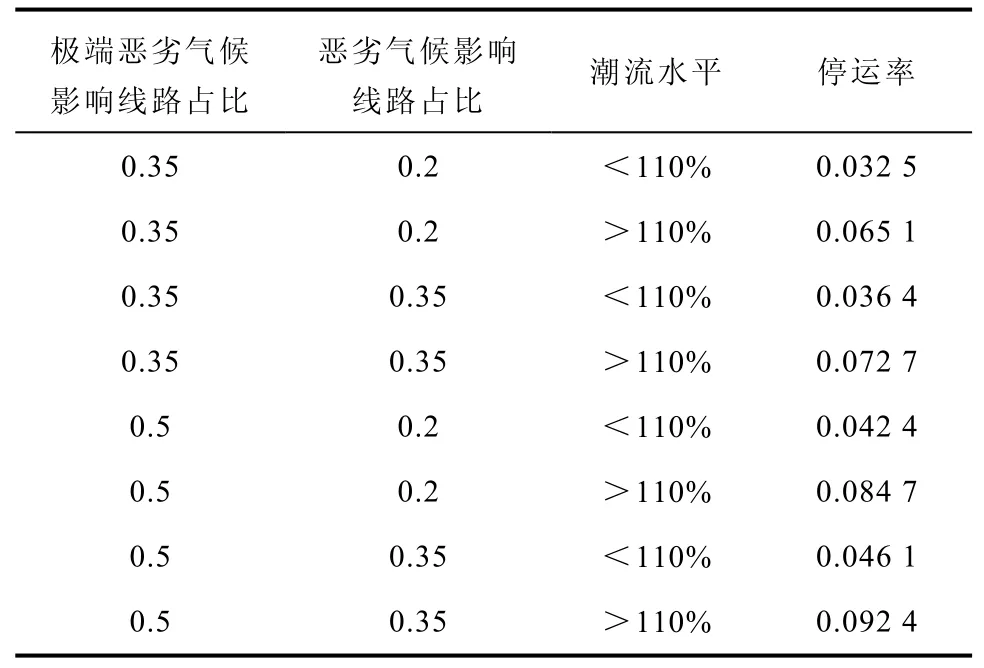
表5　if-then模糊推理规则Tab.5 Fuzzy rule of if-then

采用中心平均加权解模糊化方法，在冰力荷载单独作用下，线路综合停运率λice的模糊推理过程如图6所示。可以得到只考虑冰力荷载作用下，当线路 46%的长度处于极端恶劣气候条件，28%的长度处于恶劣气候条件，剩下26%的长度处于正常气候条件，线路潮流水平为 102%，线路此时综合停运率为0.059次/(h·50km)。

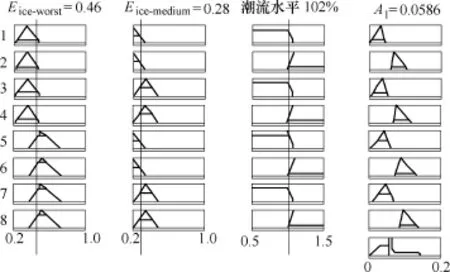
图6　只考虑冰力荷载作用时的Mamdani推理过程Fig.6 Analysis of the effect of ice on outage rate using Mamdani inference method

如果不采用模糊专家系统求解线路的分段模型，而是运用传统的解析法求解，代入式（6）得到受冰力荷载影响下线路停运率λice为

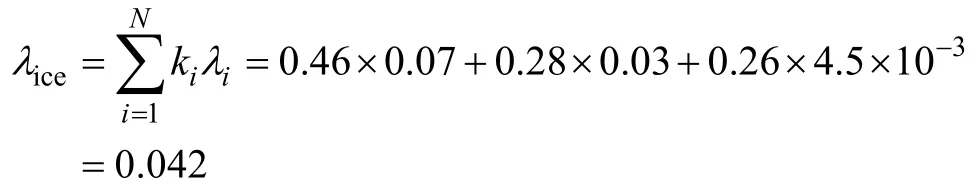
同理，可以将风力荷载作用条件下线路分段模糊化。模糊输入变量为在此条件下极端恶劣气象条件影响范围、恶劣气象条件影响范围和线路潮流水平，输入值分别为 0.4、0.4和 0.2。模糊推理过程如图7所示。只考虑风力荷载作用时，采用中心平均加权解模糊化方法得到线路此时的综合停运率λwind=0.025次/(h·50km)。

图7　只考虑风力荷载作用时Mamdani推理过程Fig.7 Analysis of the effect of wind on outage rate using Mamdani inference method

如果不采用模糊专家系统求解线路的分段模型，而是运用传统的解析法求解，代入式（6）得到受风力荷载影响下线路停运率λwind为

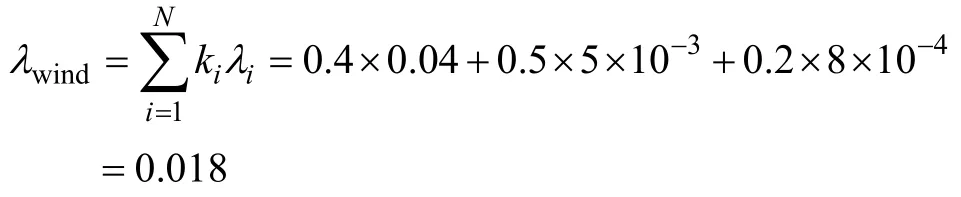
当冰力荷载和风力荷载共同影响线路停运率时，其综合影响可由式（8）加以整合。本文取εice=0.7、εwind=0.3。线路受冰、风灾害影响下的综合线路停运率λ为

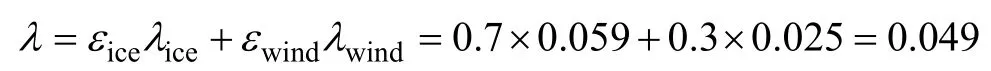
如果采用传统的解析法求解线路的综合停运率，将用解析法求得的冰力荷载和风力荷载作用下的线路停运率代入式（8）得到线路受冰风灾害影响下的综合停运率λ为

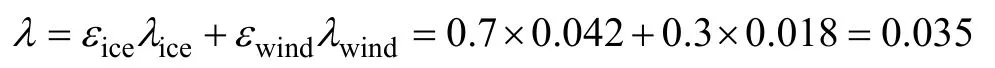
将用模糊专家系统和解析法得到的停运率结果相比较，见表6。

表6　两种方法得到的停运率比较Tab.6 Comparation of outage rates using two different approaches

可以看到，采用上述模糊规则和模糊推理系统将线路分段模型模糊化后，计算得到的线路综合停运率与线路受不同气象等级影响范围有很大关系，恶劣气象条件影响范围较大时线路停运率远高于正常气象条件影响范围较大时的停运率，仅凭统计平均值计算的线路停运率不能正确反映冰冻灾害天气对长距离输电线路可靠性的综合影响，应采用分段模拟再整合的方法。

比较传统解析法和模糊专家系统求出的同样气象条件下的线路综合停运率，可以看出基于解析法建立的模型计算结果与实际差异较大。原因在于采用传统解析法，某点所处的气象条件有极端恶劣、恶劣和正常。在这三个元素组成的集合中必居其一，且仅居其一。然而，这种方法不能反映外沿不分明的“模糊概念”。对于冰风暴灾害，其气候条件的恶劣程度用模糊语言可以更好地表达，在统计数据缺失的情况下利用输电线路停运率建模是优选方案。

5 结论

本文较详细分析了冰冻天气下输电线路停运率建模问题。首先建立计及地形因素影响的冰力荷载模型和计及覆冰影响的风力荷载模型。由于同一线路不同地段气象条件的差异性，采取对线路进行分段模拟再综合求出线路在冰、风暴灾害中的实时停运率。针对历史数据不完善的问题，基于模糊专家系统构建线路元件的非解析可靠性模型。结合专家知识和经验，采用Mamdani型推理，提出专家系统中模糊集、隶属度函数和模糊规则的确定方式。通过分析IEEE RBTS系统的线路综合故障率，说明了所提出的线路非解析元件可靠性模型比原来的解析法更加合理、准确。该方法可帮助调度人员在短期运行规划和在线运行中作出合理的决策。

[1] 陆佳政, 张红先, 彭继文, 等. 基于皮尔逊Ⅲ型概率分布的湖南电网覆冰重现期计算[J]. 电工技术学报, 2013, 28(1): 80-86. Lu Jiazheng, Zhang Hongxian, Peng Jiwen, et al. Calculation of Hunan power grid icing recurrence interval based on pearson III type probability distribution[J].Transactions of China Electrotechnical Society, 2013, 28(1): 80-86.

[2] 陆佳政, 蒋正龙, 雷红才, 等. 湖南电网2008年冰灾事故分析[J]. 电力系统自动化, 2008, 32(11): 16-19. Lu Jiazheng, Jiang Zhenglong, Lei Hongcai, et al. Analysis of Hunan power grid ice disaster accident in 2008[J]. Automation of Electric Power Systems, 2008, 32 (11): 16-19.

[3] 张满, 蒋兴良, 舒立春, 等. 混合凇对分裂导线起晕电压影响[J]. 电工技术学报, 2015, 30(3): 258-267. Zhang Man, Jiang Xingliang, Shu Lichun, et al. The influences of mixed-phase ice on corona inception voltage of bundle conductor[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 258-267.

[4] 马丽叶, 贾彬, 卢志刚, 等. 基于静态安全性和实时供电能力的输电网安全等级研究[J]. 电工技术学报, 2014, 29(6): 229-238. Ma Liye, Jia Bin, Lu Zhigang, et al. Research on security classification of transmission network considering static security and real-time power supply capability[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 229-238.

[5] Brostrom E, Ahlberg J, Soder L. Modelling of ice storms and their impact applied to a part of the Swedish transmission network[C]//Power Tech, IEEE Lausanne, 2007: 1593-1598.

[6] 陆佳政, 张红先, 方针, 等. 湖南电力系统冰灾监测结果及其分析[J]. 电力系统保护与控制, 2009, 37(12): 99-105. Lu Jiazheng, Zhang Hongxian, Fang Zhen, et al. Mechanical result and its analysis of ice disaster monitoring of Hunan power system[J]. Power System Protection and Control, 2009, 37(12): 99-105.

[7] Liu Haitao, Sun Yuanzhang, Cheng Lin, et al. Online short-term reliability evaluation using fast sorting technique[J]. IET Generation, Transmission & Distribution, 2008, 2(1): 139-148.

[8] 陈永进, 任震, 黄雯莹. 考虑天气变化的可靠性评估模型与分析[J]. 电力系统自动化, 2004, 28(21): 17-21. Chen Yongjin, Ren Zhen, Huang Wenying. Model and analysis of power system reliability evaluation considering weather change[J]. Automation of Electric Power Systems, 2004, 28(21): 17-21.

[9] Billinton R, Wu Chenjian. Predictive reliability assessment of distribution systems including extreme adverse weather[C]//Conference on Electrical and Computer Engineering, 2001, 2(2): 719-724.

[10] Billinton R, Singh G. Application of adverse and extreme adverse weather: modeling in transmission and distribution system reliability evaluation[J]. Proceedings of IEE Generation, Transmission and Distribution, 2006, 153(1): 115-120.

[11] 何剑, 程林, 孙元章, 等. 计及天气预测的电力系统运行可靠性短期评估[J]. 电力系统保护与控制, 2010, 38(10): 31-38. He Jian, Cheng Lin, Sun Yuanzhang, et al. Power system short-term operational reliability evaluation considering weather forecast[J]. Power System Protection and Control, 2010, 38(10): 31-38.

[12] 孙荣富, 程林, 孙元章. 基于恶劣气候条件的停运率建模及电网充裕度评估[J]. 电力系统自动化, 2009, 33(13): 7-12. Sun Rongfu, Cheng Lin, Sun Yuanzhang. An outage rate model and system adequacy assessment based on adverse weather conditions[J]. Automation of Electric Power Systems, 2009, 33(13): 7-12.

[13] 邹欣, 孙元章, 程林. 基于模糊专家系统的输电线路非解析可靠性模型[J]. 电力系统保护与控制, 2011, 39(19): 13-20. Zou Xin, Sun Yuanzhang, Cheng Lin. Non-analytic reliability model of transmission lines based on fuzzy expert system[J]. Power System Protection and Control, 2011, 39(19): 13-20.

[14] 韩卫恒, 刘俊勇, 张建明, 等. 冰冻灾害下计入地形及冰厚影响的分时段电网可靠性分析[J]. 电力系统保护与控制, 2010, 38(15): 81-86.Han Weiheng, Liu Junyong, Zhang Jianming, et al. Power system time-section reliability assessment analysis considering topography and icing under freezing disasterweather[J]. Power System Protection and Control, 2010, 38(15): 81-86.

[15] 李文沅. 电力系统风险评估模型、方法和应用[M].北京: 科学出版社, 2006.

[16] Lu C, Shen C. Estimation of sensitive equipment disruptions due to voltage sags[J]. IEEE Transactions on Power Delivery, 2007, 22(2): 1132-1137.

[17] Shen C, Lu C. A voltage sag index considering compatibility between equipment and supply[J]. IEEE Transactions on Power Delivery, 2007, 22(2): 996-1002.

[18] Li W, Zhou J, Xiong X. Fuzzy models of overhead power line weather-related outages[J]. IEEE Transactions on Power System, 2008, 23(3): 1529-1531.

Piecewise Equivalent Model of Ice Disaster Impact on Outage Rate of Transmission Lines Using Fuzzy Expert System

Duan Jie Wang Xiuli Hou Yushen
（Department of Electrical Engineering Xi’an Jiaotong University Xi’an 710049 China）

Transmission lines always cross long distance. As different parts of a transmission line may confront different weather conditions at the same time, a piecewise equivalent model is introduced to calculate the outage rate. The transmission line is divided into segments in series according to their particular external environment and their corresponding outage rates. Then these segments are combined to form an integrated outage rate for the entire transmission line. Taken the uncertainty of weather forecast and system operating status into account, the analytical model between load and outage is converted into a fuzzy one. It contains fuzzy sets, membership functions and fuzzy “if-then”rules, to effectively solve the problems caused by inaccurate data. The new model is applied to IEEE RBTS system. Assuming that a specified transmission line confronts three types of external load pressure in different parts, the outrage rates of the transmission lines are calculated and compared. With the deterioration of the weather condition and system operating state, the outrage rates of the transmission lines increase. The proposed model provides of the foundation for operational risk assessments of transmission lines and power system reliability.

Transmission line outage rate, piecewise model, fuzzy expert system, wind load, ice load

TM734

段 杰 男，1989年生，硕士研究生，研究方向为电力系统可靠性和电力系统优化规划。

E-mail: schzdj@163.com

侯雨伸 男，1988年生，博士研究生，研究方向为电力系统优化规划。

E-mail: houyushen20039@126.com（通信作者）

国家自然科学基金资助项目（51277140）。

2014-05-05 改稿日期 2014-08-12