基于Flatjoint接触模型的岩石单轴压缩和巴西劈裂颗粒流模拟研究

刘富有，陈鹏宇，余宏明

(1.中国地质大学(武汉) 工程学院，武汉　430074；2.河南省地质矿产勘查开发局 第二地质矿产调查院，郑州　450000；3.内江师范学院　地理与资源科学学院，四川 内江　641100)



基于Flatjoint接触模型的岩石单轴压缩和巴西劈裂颗粒流模拟研究

刘富有1,2，陈鹏宇3，余宏明1

(1.中国地质大学(武汉) 工程学院，武汉430074；2.河南省地质矿产勘查开发局 第二地质矿产调查院，郑州450000；3.内江师范学院地理与资源科学学院，四川 内江641100)

基于颗粒流平台，选择Flatjoint接触模型作为岩石模拟的基本模型，用单轴压缩和巴西劈裂数值试验测试岩石宏观参数，对数值试验进行正交设计，采用多因素方差分析和回归分析研究宏细观参数之间的关系。在此基础上，提出了基于岩石单轴压缩和巴西劈裂数值试验的细观参数匹配方法。以灰岩的室内试验为基础，对灰岩细观参数进行了标定，实现了灰岩单轴压缩和巴西劈裂的颗粒流模拟，模拟结果与试验结果相接近，验证了本文方法的有效性。

岩石；颗粒流；Flatjoint接触模型；单轴压缩；巴西劈裂

1　研究背景

颗粒流程序(particleflowcode，PFC)是一种离散单元法，其通过圆形颗粒之间的相互作用来模拟材料的宏观力学性质。最初，颗粒流程序中只有接触黏结模型和平行黏结模型2种颗粒接触黏结模型[1]。在实际应用中发现这2种模型计算得出的单轴抗拉强度都较高，导致单轴抗压强度和单轴抗拉强度比值UCS/TS值为3～4。而对于很多岩石，UCS/TS常常超过10。为此，N.Cho等[2]提出了簇平行黏结模型，它将多个颗粒固结成簇，形成一个不规则的大颗粒，簇中单个颗粒的旋转被抑制，这使UCS/TS值显著增大。为了更好地解决这个问题，D.O.Potyondy[3]又提出了一种适用于硬质岩石的平直节理颗粒黏结模型(Flat-JointedBonded-ParticleMaterial,FJBPM)，平直节理颗粒黏结模型将圆形颗粒构造成多边形颗粒，颗粒破坏后的旋转被抑制。随着颗粒流数值模拟方法的发展，其应用范围也越来越广泛，特别是岩石破坏的细观模拟分析[4-6]。但是上述方法大都采用颗粒流程序中的平行黏结模型。为此，本文选用FJBPM作为基本模型，研究宏细观参数之间的关系，提出了细观参数的匹配方法，在此基础上进行了灰岩单轴压缩与巴西劈裂破坏的颗粒流模拟。

2　颗粒流基本理论

PFC2D中通过设置每个接触的本构模型，从而实现对岩石材料宏观本构性质的模拟。Flatjoint接触模型能够抑制黏结破坏后颗粒的旋转。典型的Flatjoint接触模型如图1所示。

(a)假设的多边形颗粒形态

(b)平直节理交界面形态图1　平直节理接触模型[3]Fig.1　Flatjoint contact model[3]

Flatjoint接触模型有未黏结和黏结2种模式，两者的本构关系不同，具体可参见文献[3]。

选定Flatjoint接触模型，可通过岩石数值试验与室内物理试验的对比进行细观参数的标定。单轴压缩数值试验是经宏观参数得到细观参数的最重要的途径之一，该数值试验主要可以得到单轴抗压强度、变形模量和泊松比等参数；另一个确定细观参数的重要数值试验就是巴西劈裂数值试验。根据数值试样破裂时的峰值作用力Ff，可得数值试样的抗拉强度。本文选择这2个数值试验作为细观参数标定的基础。

3　细观参数的标定

3.1正交试验设计

在进行正交试验设计之前，考虑到接触本构模型细观参数较多，增加了数值试验的数量和细观参数标定的难度，因此，有必要进行一定的假设，以减少细观参数的数量。Flatjoint接触模型的细观参数包括：N，Ec，kn/ks，μb，λ，σb，cb，φb。其中：N为交界面段数；Ec为平直节理模量；kn/ks为平直节理刚度比；μb为平直节理摩擦系数；λ为平直节理两端较小颗粒的半径比；σb为平直节理抗拉强度；cb为平直节理黏聚力；φb为平直节理内摩擦角。

参考D.O.Potyondy[3]，B.A.Poulsenn等[7]的研究，作以下假设：①平直节理抗拉强度σb小于抗剪强度τb，即σb<τb=cb+σtanφb，σ为平直节理所受正应力，可获得符合实际的岩石拉压强度比；②采用简化的平直节理破坏准则，即τb=cb，φb=0，可以有效控制平直节理抗剪强度与抗拉强度比；③平直节理抗拉强度和抗剪强度两者的标准差与平均值的比值相等，取SD/Mean=0.25；④平直节理两端较小颗粒的半径比λ=1；⑤取最小半径Rmin=0.4mm，颗粒半径比固定为1.66；⑥平直节理摩擦系数μ=0.5。

由此，根据所需确定的细观参数建立正交试验设计表1，设计的正交矩阵序列如表2所示。分别进行单轴压缩数值试验和直接拉伸数值试验(试样宽50mm，高100mm)，由此得到宏观参数：单轴抗压强度σf、弹性模量E、泊松比ν和抗拉强度σt，所得结果如表2所示，可以看出该结果符合大部分岩石的宏观参数取值范围，并且平直节理模型的压拉比σf/σt大部分满足10～20。

3.2多因素方差分析

采用SPSS软件对表2的数据进行多因素方差分析。图2给出了多因素方差分析的F统计量的结果，其中X1表示Ec，X2表示kn/ks，X3表示σb，X4表示τb/σb，X5表示N。

表1　Flatjoint接触模型细观参数正交试验设计值Table 1　Orthogonal experimental design of mesoscopicparameters of Flatjoint model

表2　Flatjoint接触模型细观参数正交设计的矩阵序列和 宏观参数计算结果Table 2　Orthogonal matrix sequence of mesoscopic parametersof Flat-jointed model and the corresponding macroscopicparameters

根据F统计量和相伴概率值Sig.的结果(取显著性水平为α=0.05)可得到宏观参数的显著性影响因素及其排序结果如下：①弹性模量E,Ec>kn/ks>N；②泊松比υ,kn/ks>τb/σb;③单轴抗压强度σf,σb>τb/σb>N;④抗拉强度σt,σb>kn/ks;⑤压拉强度比σf/σt,τb/σb>kn/ks。

根据图2的结果，可以得到以下结论：

(1)对于平直节理模型，弹性模量E主要受到节理模量Ec、节理刚度比kn/ks和交界面段数N的影响，其中以节理模量Ec最为显著，节理刚度比kn/ks次之，交界面段数N的影响相对较弱，可以忽略。

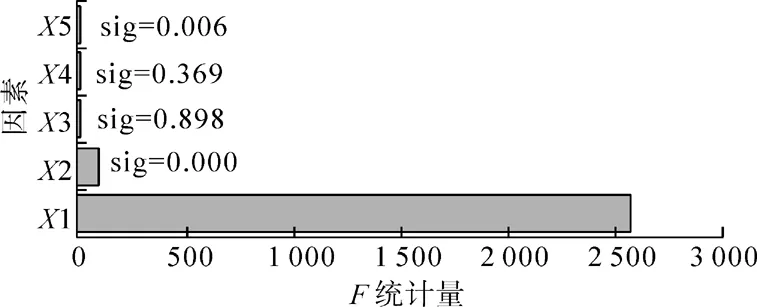
(a)弹性模量E

(b)泊松比υ

(c)单轴抗压强度σf

(d)抗拉强度σt

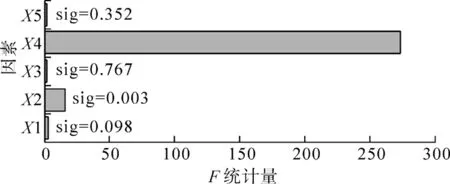
(e)压拉强度比σf/σt图2　平直节理模型宏细观参数多因素方差分析的F统计量Fig.2　F statistics of multi-factor analysis of variance formacro-and-meso-scopic parameters of Flatjoint model

(2)泊松比υ主要受到节理刚度比kn/ks和节理强度比τb/σb的影响，节理刚度比kn/ks的影响远大于节理强度比τb/σb。

(3)单轴抗压强度主要受到节理抗拉强度σb、强度比τb/σb和交界面段数N的影响，以节理抗拉强度σb最为显著，节理强度比τb/σb次之，交界面段数N影响最弱。

(4)抗拉强度σt主要受到节理抗拉强度σb和节理刚度比kn/ks的影响，但是节理刚度比kn/ks相比于节理抗拉强度影响较弱，可以忽略。

(5)压拉强度比σf/σt主要受到节理强度比τb/σb和节理刚度比kn/ks的影响，节理强度比τb/σb的影响远大于节理刚度比kn/ks。

3.3回归分析

根据上述正交试验计算结果可以建立宏观参数与其主要显著影响因素之间的关系式如表3所示，其中由于交界面段数N对宏观参数的影响相对于其他参数较小，并未考虑该因素。可以看出，宏观参数拟合公式的R2值在0.917～0.992之间，说明拟合效果良好，能够比较准确反映宏观参数与细观参数之间的关系。其中，弹性模量E与节理模量Ec呈正相关关系，与节理刚度比kn/ks的自然对数呈负相关关系；泊松比v与节理刚度比kn/ks和强度比τb/σb呈正相关关系；单轴抗压强度σf与节理抗拉强度σb和强度比τb/σb呈正相关关系；抗拉强度σt与节理抗拉强度σb呈正相关关系；压拉强度比σf/σt与节理刚度比kn/ks和强度比τb/σb呈正相关关系。

表3　宏观参数与细观参数之间的关系式及拟合度Table 3　Regression equations of macro-and-meso-scopicparameters and corresponding degrees of fitting

根据表3中的拟合公式，在已知宏观参数的情况下，即可反算对应的细观参数，由于σf/σt，σf，σt三者之间具有相关性，选择其中2个公式即可，为了计算方便，选择σf，σt两者的拟合公式，得到反算公式如表4所示。至于交界面段数N，可选择为3～4[3,7]，根据反算公式初步计算细观参数，然后进行数值试验计算宏观参数，对比计算宏观参数与实际宏观参数之间的差别，再根据拟合公式中所反映的宏细观参数之间的趋势性关系，可对细观参数进行适当微调，直到达到合理的精度范围。

表4　细观参数的反算公式Table 4　Back calculation formulas for mesoscopicparameters

4　实例分析

4.1室内试验

采用焦作市龙寺废弃矿山奥陶系中统上马家沟组(O2s)厚层状灰岩，室内试验是在INSTORN-1346电液伺服岩石力学测试系统上进行，可自动计算宏观力学参数。

4.1.1单轴压缩试验

图3为试验过程中测试系统自动记录的部分应力-应变曲线，从中可以看出后区曲线较陡，说明灰岩脆性明显。图4为岩石单轴压缩试验岩样破坏形态，岩样主要发生垂向的脆性劈裂破坏以及表层剥离，破坏面方向与轴向荷载加载的方向近乎平行。表5中给出了岩石单轴压缩试验成果。

(a)Y-1编号

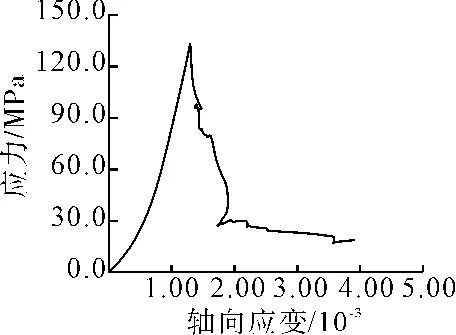
(b)Y-2编号图3　岩石单轴压缩应力-应变曲线Fig.3　Stress-strain curves of rock uniaxial compressive test

图4　岩石单轴压缩试验岩样破坏形态Fig.4　Failure patterns of rock samples under uniaxialcompression test表5　岩石单轴压缩试验成果Table 5　Result of rock uniaxial compression test

编号抗压强度/MPa试验结果均值弹性模量/GPa试验结果均值泊松比试验结果均值Y-1111.98Y-2133.55Y-3122.17Y-4119.96121.9172.9668.4051.8751.9061.280.2020.2050.2190.2070.208

4.1.2岩石巴西劈裂试验

巴西破裂试验同样是在INSTORN-1346电液伺服岩石力学测试系统上进行，可自动计算岩样抗拉强度。图5为试验过程中测试系统自动记录的部分应力-应变曲线，从中可以看出曲线呈倒V形，反映了灰岩的硬脆性特征。图6为岩石巴西劈裂试验岩样破坏形态，岩样主要发生径向的脆性劈裂破坏，破坏面方向与轴向荷载加载的方向平行。表6给出了岩石巴西劈裂试验成果。

(a) L-1

(b)L-2图5　岩石巴西劈裂应力-应变曲线Fig.5　Stress-strain curves of rock brazilian splitting test

图6　岩石巴西劈裂试验岩样破坏形态Fig.6　Failure patterns of rock samples under Braziliansplitting test表6　岩石巴西劈裂试验成果Table 6　Result of rock Brazilian splitting test

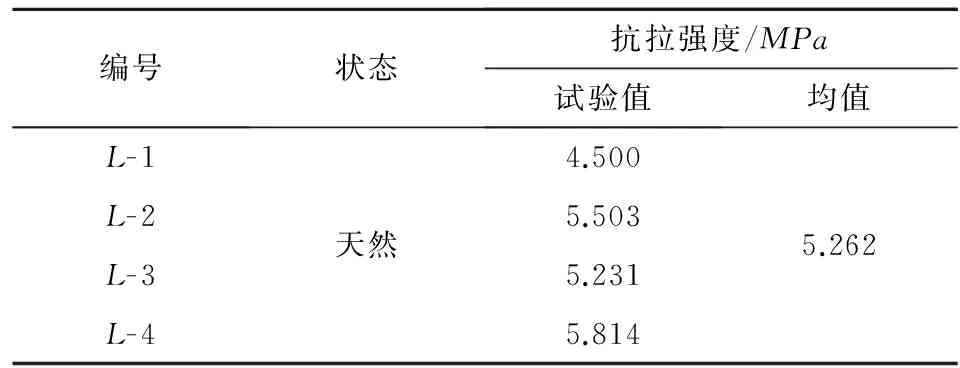
编号状态抗拉强度/MPa试验值均值L-1L-2L-3L-4天然4.5005.5035.2315.8145.262

4.2岩石破坏的颗粒流数值模拟

4.2.1岩石细观参数的标定

根据上述试验结果，即可进行岩石细观参数的标定，宏观参数选用岩石试验结果的平均值。生成颗粒流试样时，采用的空隙率为0.1，由此可以根据岩石密度确定颗粒密度，采用如下公式：

ρs=ρ/(1-r)。

(1)

式中：ρs为颗粒密度；ρ为岩石密度；r为数值试样空隙率，取0.1。

在正交试验时，本文采用的是直接拉伸试验确定抗拉强度，而岩石试验采用的是巴西劈裂试验。因此，在细观参数匹配时，采用的是巴西劈裂数值试验。巴西劈裂试验与直接拉伸试验确定的抗拉强度存在一定差异，但是差异并不是特别大，所以仍可以用表4中公式反算细观参数。然后，根据岩石单轴压缩数值试验对细观参数进行微调，以达到合理的精度范围。根据表5和表6的试验结果标定各项细观参数如表7所示，对应数值试样宏观参数如表8所示。

表7　岩石细观参数标定结果Table 7　Calibration result of rock mesoscopic parameters

表8　岩石数值试样宏观参数Table 8　Macroscopic parameters of rock numerical sample

对比表5，表6和表8 的宏观参数，从中可以看出，岩石数值试样的宏观参数和室内试验结果的平均值是非常接近的，误差仅在0.48%～2.51%之间。

4.2.2数值模拟结果分析

4.2.2.1单轴压缩数值试验

图7是PFC2D模拟的灰岩单轴压缩破坏过程的数值模拟结果。从图中可以看出，数值试样的破坏主要表现为轴向劈裂以及表层剥离，这与岩石试验结果是非常一致的。从应力-应变曲线中可以看出后区曲线较陡，这与室内试验结果一致，说明数值试样能够很好地体现灰岩的脆性特征。

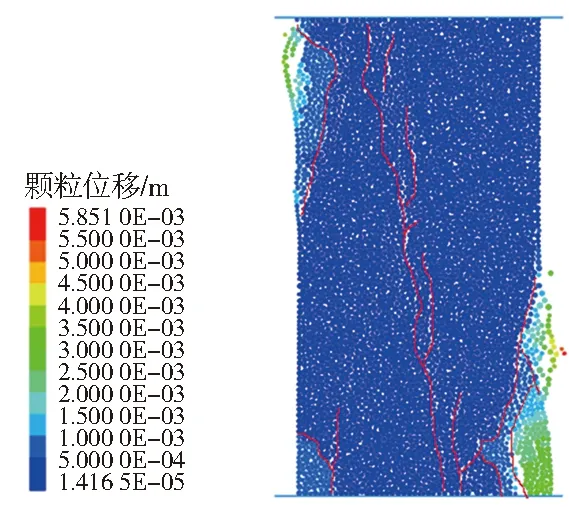
(a)破坏试样

(b)应力-应变曲线图7　灰岩单轴压缩数值模拟结果Fig.7　Numerical simulation result of uniaxial compressiontest of limestone

4.2.2.2巴西劈裂数值试验

图8是PFC2D模拟的灰岩巴西劈裂破坏过程的数值模拟结果。从图中可以看出，数值试样的破坏主要表现为径向的劈裂破坏，这与岩石试验结果是非常一致的。从应力-应变曲线中可以看出后区曲线较陡，这与室内试验结果一致，说明数值试样能够很好地体现灰岩的脆性特征。

(a)破坏试样

(b)荷载-应变曲线图8　灰岩巴西劈裂数值模拟结果Fig.8　Numerical simulation result of Brazilian splittingtest of limestone

5　结　论

(1)采用正交试验设计和多因素方差分析研究岩石细观参数和宏观参数之间的关系，得到如下结论：弹性模量E主要受节理模量Ec、节理刚度比kn/ks和交界面段数N的影响，显著性排序为Ec>kn/ks>N；泊松比v主要受节理刚度比kn/ks和节理强度比τb/σb的影响，显著性排序为kn/ks>τb/σb；单轴抗压强度主要受节理抗拉强度σb、强度比τb/σb和交界面段数N的影响，显著性排序为σb>τb/σb>N；抗拉强度σt主要受节理抗拉强度和节理刚度比的影响，显著性排序为σb>kn/ks；压拉强度比σf/σt主要受到节理强度比τb/σb和节理刚度比kn/ks的影响，显著性排序为τb/σb>kn/ks。

(2)根据正交试验计算结果可以建立宏观参数与其主要显著影响因素之间的关系式，发现弹性模量E与节理模量Ec呈正相关关系，与节理刚度比kn/ks的自然对数呈负相关关系；泊松比v与节理刚度比kn/ks和节理强度比τb/σb呈正相关关系；单轴抗压强度σf与节理抗拉强度σb和节理强度比τb/σb呈正相关关系；抗拉强度σt与节理抗拉强度σb呈正相关关系；压拉强度比σf/σt与节理刚度比kn/ks和节理强度比τb/σb呈正相关关系。根据宏细观参数之间的拟合公式得到了细观参数的反算公式，由此建立了岩石细观参数的标定方法。

(3)进行了灰岩的单轴压缩与巴西劈裂试验，试验结果显示灰岩的脆性特征明显。单轴压缩主要发生垂向的脆性劈裂破坏以及表层剥离，破坏面方向与轴向荷载加载的方向近乎平行。巴西劈裂主要发生径向的脆性劈裂破坏，破坏面方向与轴向荷载加载的方向平行。建立了灰岩的单轴压缩与巴西劈裂数值模型，模拟结果显示FJBPM可以很好地体现灰岩的脆性破坏特征，数值模拟结果与室内试验结果比较接近，说明了本文方法的有效性。

[1]POTYONDYDO,CUNDALLPA.ABonded-particleModelforRock[J].InternationalJournalofRockMechanicsandMiningSciences,2004,41(8):1329-1364.

[2]CHON,MARTINCD,SEGODC.AClumpedParticleModelforRock[J].InternationalJournalofRockMechanicsandMiningSciences,2007,44(7):997-1010.

[3]POTYONDYDO.AFlat-jointedBonded-particleMaterialforHardRock[C]//AmericanRockMechanicsAssociation,Proceedingsofthe46thUSRockMechanics/Geome-chanicsSymposium,Chicago,IL,USA,June24-27,2012:1510-1519.

[4]张学朋，王刚，蒋宇静，等.基于颗粒离散元模型的花岗岩压缩试验模拟研究[J].岩土力学，2014，35(增1)：99-105.

[5]刘宁，张春生，褚卫江，等.深埋大理岩脆性破裂细观特征分析[J].岩石力学与工程学报，2012，31(增2)：3557-3565.

[6]唐谦，李云安.围压对岩石裂纹扩展影响的颗粒流模拟研究[J].长江科学院院报，2015，32(4)：81-85.

[7]POULSENNBA,ADHIKARYDP.ANumericalStudyoftheScaleEffectinCoalStrength[J].InternationalJournalofRockMechanics&MiningSciences,2013,63:62-71.

(编辑：刘运飞)

PFC Simulation of Uniaxial Compression and Brazilian Splitting Test ofRock Based on Flat-jointed Bonded-particle Material

LIU Fu-you1,2,CHEN Peng-yu3,YU Hong-ming1

(1.FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China;2.No.2InstituteofGeological&MineralResourcesofHenanProvince,Zhengzhou450000,China;3.SchoolofGeographyandResourcesScience,NeijiangNormalUniversity,Neijiang641100,China)

TheFlat-jointbonded-particlematerialwasselectedasthebasicmodelforrocksimulation.Themacro-parametersofrockwerecalculatedthroughnumericaluniaxialcompressiontestandBraziliansplittingtestinPFC.Orthogonaldesignwasadoptedtoconductnumericaltestsandmulti-factoranalysisofvarianceandregressionanalysiswereutilizedtoanalyzetherelationshipbetweenmacro-parametersandmeso-parameters.Onthisbasis,methodofmatchingthemeso-parametersfornumericaluniaxialcompressiontestandBraziliansplittingtestwasproposed.Accordingtolaboratorytestsoflimestone,themeso-parametersoflimestonewereobtainedandthePFCsimulationofuniaxialcompressionandBraziliansplittingtestsoflimestonewereconducted.Thesimulationresultsareclosetothelaboratorytestresults,whichvalidatedtheeffectivenessoftheproposedmethod.

rock;PFC;Flatjointcontactmodel;uniaxialcompression;Braziliansplitting

2015-07-07;

2015-10-12

国家自然科学基金项目(41272377，41302278)

刘富有(1968-),男,河南邓州人,教授级高级工程师,博士，主要从事工程地质、水文地质和环境地质方面的工作，(电话)0371-55156812(电子信箱)79012983@qq.com。

10.11988/ckyyb.20150566

2016,33(09):60-65

TU457

A

1001-5485(2016)09-0060-06