零售商品销售量组合预测研究

昆明理工大学质量发展研究院 郭栋 李红娟 桑秀丽

零售商品销售量组合预测研究

昆明理工大学质量发展研究院 郭栋 李红娟 桑秀丽

针对零售商品销售量预测精度不高，致使零售商蒙受经济损失的问题，本文提出ARIMA-GARCH与Elman神经网络的零售商品销售量组合预测模型。先利用ARIMA-GARCH对存在异方差的零售商品销售量非平稳序列进行线性预测，再利用Elman神经网络对销售序列进行非线性预测；最后，结合线性规划思想，运用误差绝对值最小赋权算法实现对零售商品销售量的精确预测。案例分析表明，与ARIMA、BP等模型相比，该组合模型预测精度更高，更适合零售商品销售量的预测，在以后的零售商品销售预测中具有一定的推广作用。

零售商品销售量 ARIMA-GARCH Elman神经网络 组合预测

零售商品销售是零售行业管理中最为重要的部分之一，零售商品销售预测能为零售商的生产、运输、配送提供指导，提高经济效益，然而现实生活中往往因为销售预测精度不高带来种种问题，比如，积压时间过长导致商品过期和浪费；供应不足导致消费者投诉和影响零售商声誉等［1］。因此，对零售商品销售量进行精确预测，一方面可以有针对性地进行零售商品生产，为消费者提供充足的货物保障；另一方面有利于零售商进行合理采购，避免浪费或积压。

目前，研究零售商品销售预测的方法有两种，一种为单一预测法，诸如ARIMA［2］、灰色预测［3］、神经网络［4］、支持向量机［5］等方法。另一种为组合预测法，诸如灰色预测和支持向量机结合［6］、ARIMA与BP神经网络结合［7］、灰色模型与RBF神经网络结合［8］等方法。虽然预测方法众多，但是，这些方法自身都存在一定的局限性。ARIMA法简单方便，却不能解决方差非齐性（异方差）问题。灰色预测法所需样本量少，计算快捷，却要求样本序列光滑离散。BP神经网络与支持向量机表现出相对较高的预测精度，却训练速度慢，时间较长。ARIMA-GARCH模型能很好地解决回归分析中异方差问题，并在预测领域得到广泛应用，但预测精度相比智能算法略低。Elman神经网络作为一种典型的动态回归网络，不同于BP和RBF神经网络，其在BP神经网络结构的基础上，通过存储内部状态使其具有映射动态特征的功能，从而使系统具有适应时变特性的能力，但没有传统算法那样可依据设计方法和原则，而网络训练和测试多采用调试法。

基于此，本文构建ARIMA-GARCH与Elman神经网络的零售商品销售量组合预测模型，该组合预测模型既发挥了传统回归分析法简单方便和智能神经网络精度较高等优点，同时又通过GARCH和Elman神经网络算法分别对异方差和训练速度慢等问题进行了修正和完善。案例分析表明，该组合预测算法不仅操作可行，而且更进一步提高了零售商品销售的预测精度。

1　预测模型的构建

1.1ARIMA-GARCH模型

ARIMA模型，适合预测具有非平稳时间序列的零售商品销售量［9］。在预测过程中通常假设误差项的条件方差不变，使其无法有效地解释零售商品销售量时间序列中的波动，为此，在模型中进一步引入GARCH模型。

GARCH模型，即广义自回归条件异方差模型，可以轻易地发现零售商品销售量时间序列变化中存在的异方差和聚类性［10］。

当ARIMA模型处理零售商品非平稳时间序列出现ARCH效应时，就需用GARCH模型对残差项的异方差问题进行修正，此时的模型即为ARIMA-GARCH模型。

1.2Elman神经网络

Elman神经网络是一种内部具有反馈结构的动态回归神经网络［11］。其网络结构主要分为四层：输入层、隐含层、承接层和输出层。Elman神经网络的误差函数为：

1.3组合预测算法

为了简单便捷且有效地提高零售商品销售量预测精度，本文提出一种基于误差绝对值最小赋权方法的最优线性零售商品销售量预测的组合优化算法。

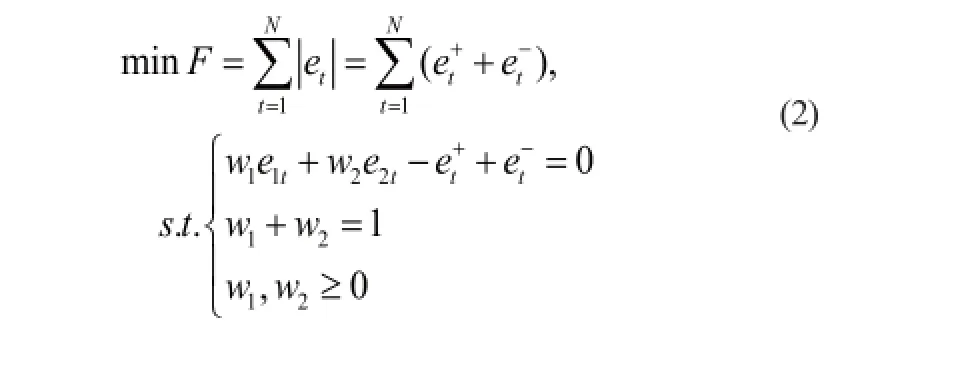
2　案例分析

2.1ARIMA-GARCH模型预测

本文选取某超市数据系统中2015年下半年7月～12月的某零售商品销售量数据（单位：千瓶）。其中，7月～11月共计153天作为训练数据，12月共31天用来做测试数据。用EViews8.0软件对训练数据进行处理并建立模型。由零售商品销售时序图（图1），可明显看出零售商品销售在10月1日～7日期间变化巨大，且11月中旬也明显异于常态，所以可判断此序列为非平稳时间序列。

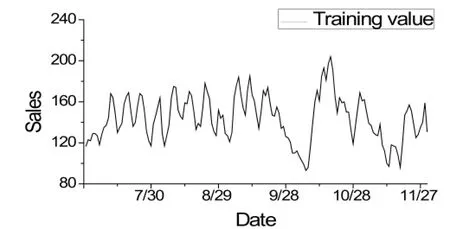
图1　时序图

对零售商品销售量序列一阶差分后，进行ADF单位根检验，由表1知DF统计量为-9.760134，远小于1%置信水平的-3.474874，且显著性p值小于0.05，因此可认为该序列已平稳。由图2可初步确定ARIMA模型的p、q值，尝试构建ARIMA（1，1，2）模型。

表1　ADF单位根检验结果

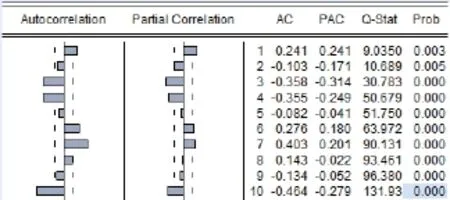
图2　1阶自相关图

在构建ARIMA-GARCH模型前，由图2中Q统计量异常显著，可知序列存在ARCH效应，对ARIMA（1，1，2）残差应进行ARCHLM检验，由表2可知，LM统计量的显著性P值为0.007，远小于0.05，即ARCH效应显著，可构建ARIMA-GARCH模型用于零售商品销售量预测。

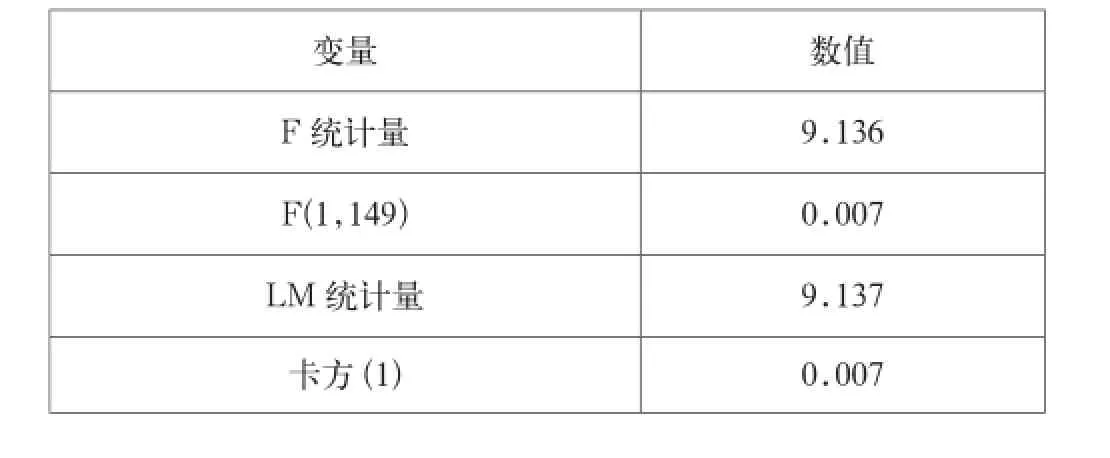
表2　ARCH效应LM检验法

2.2Elman神经网络预测

由于零售商品销售量对外界影响因素敏感，较大波动容易使Elman神经网络出现过拟合现象，同时为了加快神经网络的收敛速度，需对零售商品销售量数据进行归一化，使其归一化在［0.1，0.9］之间。

零售商品销售量数据是一维时间序列，前期销售序列会对后期造成影响，于是用逐步拓阶法来设计Elman神经网络的输入和输出，得到重组销售数据，前150组数据用于Elman神经网络学习训练，方法采用自适应学习速率的动量梯度下降反向传播算法；后31组用于测试。模型输入个数为3，隐含层神经元个数为9，输出数个数为1。用MATLAB编程得到训练结果如图3所示。从均方误差图看出，Elman神经网络训练效果较好，即Elman神经网络可用于对零售商品销售量测试集进行预测。

图3　训练结果

2.3组合预测

通过ARIMA-GARCH和Elman神经网络分别对零售商品销售量进行单项预测，得到测试数据的预测值。易知，单项模型的总数、测试集的总数、第个模型的预测值以及第个模型的误差值。再由组合优化算法，通过MATLAB线性规划模块计算出结果，得到最优解为：

2.4误差分析

科学合理的误差评价指标对评定预测效果十分重要，本文采用平均绝对相对误差（MAPE）和均方误差（MSE）作为误差评定指标。为了验证本文所建模型的优越性，运用ARIMA、BP神经网络等模型进行预测精度对比研究。对比结果如表3所示。

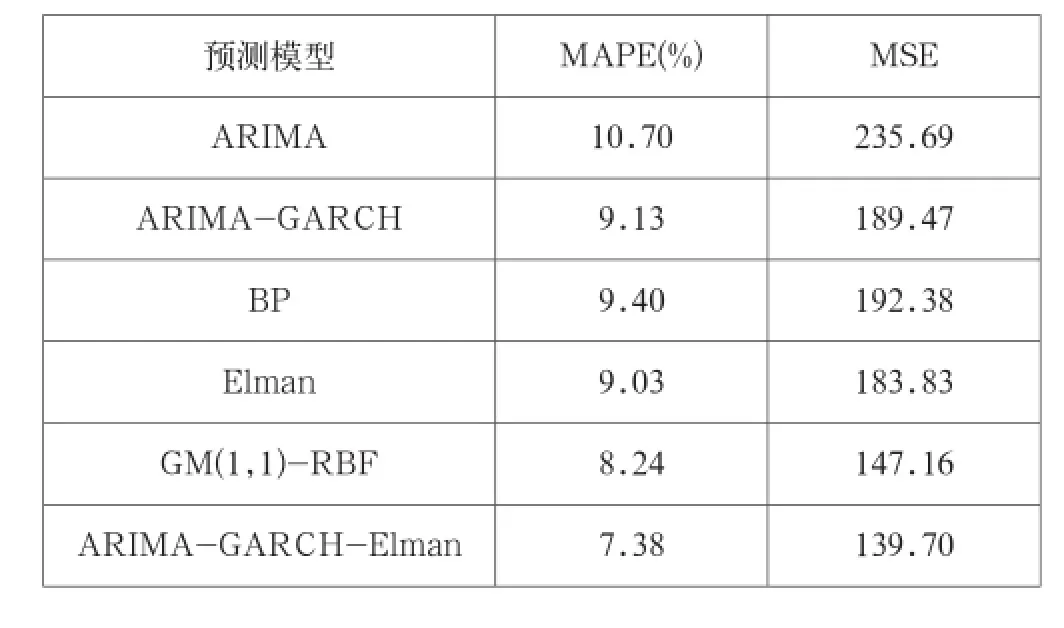
表3　预测误差分析

由表3可知，ARIMA-GARCH的MAPE和MSE值均小于ARIMA，说明引入GARCH模型使得模型预测精度提升；Elman预测精度要高于BP，说明动态神经网络在零售商品预测效果上优于静态神经网络； ARIMA-GARCH-Elman的MAPE、MSE值最小，说明本文提出的组合预测模型相对于以往的预测模型，其预测精度更高，更适合零售商品销售量的预测。

3　结语

精确有效地预测零售商品销售量对商家意义重大。本文针对零售商品销售的波动性、非平稳性，提出ARIMA-GARCH与Elman神经网络的组合预测模型。该模型既结合传统预测模型简捷的优势，又发挥了智能算法预测准确的长处。与ARIMA、BP等模型相比，本文提出的模型更适合于零售商品销售量。

［1］ Aye G C，Balcilar M，Gupta R，et al.Forecasting aggregate retail sales：The case of South Africa［J］. International Journal of Production Economics，2013（160）.

［2］ Ramos P，Santos N，Rui R.Performance of state space and ARIMA models for consumer retail sales forecasting［J］.Robotics and Computer-Integrated Manufacturing，2015（34）.

［3］ 李家会.灰色预测模型在产品销售预测中的应用［J］.科技信息，2014（11）.

［4］ Vhatkar S，Dias J.Oral-Care Goods Sales Forecasting Using Artificial Neural Network Model［J］.Procedia Computer Science，2016（79）.

［5］ 李哲，肖汉杰，李红娟.支持向量机在企业冰箱订单需求中的应用［J］.中国商论，2015（3）.

［6］ 张清华，刘凤英.基于灰色预测和支持向量机的销售预测模型研究［J］.中国商论，2013（9）.

［7］ 张昉，周宗放.基于ARIMA模型和BP神经网络的销售组合预测研究［J］.管理学家：学术版，2009（4）.

［8］ 盛魁.无偏灰色RBF神经网络组合模型在药品销售预测中的应用［J］.西南民族大学学报：自然科学版，2013（3）.

［9］ Hassan J.ARIMA and regression models for prediction of daily and monthly clearness index［J］.Renewable Energy，2014（7）.

［10］ Babu C N，Reddy B E.Prediction of selected Indian stock using a partitioning interpolation based ARIMA GARCH model［J］.Applied Computing & Informatics，2015（2）.

［11］ Zhou H，Su G，Li G.Forecasting Daily Gas Load with OIHF-Elman Neural Network［J］.Procedia Computer Science，2011（5）.

F224

A

2096-0298（2016）08（c）-001-03

郭栋（1990-），男，汉族，安徽芜湖人，硕士研究生，主要从事经济预测方面的研究；李红娟（1984-），女，汉族，辽宁省彰武县人，博士，讲师，主要从事经济数据分析方面的研究。

桑秀丽（1980-），女，山东泰安人，博士，教授，主要从事服务质量管理方面的研究。