稳定性导数计算方法研究

张瑞民，时晓天

(中国航天空气动力技术研究院 第二研究所，北京　100074)



稳定性导数计算方法研究

张瑞民，时晓天

(中国航天空气动力技术研究院 第二研究所，北京100074)

稳定性导数的准确计算对于飞行器的操稳特性具有重要意义。应用计算流体力学(CFD)方法中的非结构化动网格技术建立能够模拟飞行器做周期性俯仰运动的强迫振荡法，以国际动导数标模Finner导弹为验证算例，获得不同马赫数下俯仰力矩系数的迟滞环曲线，进而计算Finner导弹在不同马赫数下的静稳定性导数和动稳定性导数。结果表明：本文计算得到的俯仰静稳定性导数与试验数据非常接近；在亚音速和超音速范围内，动稳定性导数计算结果与试验值很接近，但在跨音速范围内，本文计算结果与试验曲线的规律性一致，但误差较大。

稳定性；导数；导弹；动网格；俯仰振荡

0　引　言

现代飞机型号设计日趋复杂，飞行条件也越来越严酷，在高速、大攻角状态下，对于带翼的细长体飞行器而言，其阻尼导数对飞行器响应具有强烈的影响[1-2]，有效、精确的性能评估对所有的型号工程系统设计都至关重要。通常，通过飞行测试来确定新型导弹的气动性能，但现代型号的复杂性使得测试过程愈加复杂，且测试费用十分昂贵；有些型号甚至出现了极端的流场状况，即使风洞试验也无法实现，而且风洞试验还存在着系统机构阻尼、支架干扰、洞壁干扰及重心位置干扰等影响，使其无法满足未来的工程型号需求。

CFD技术不仅消除了飞行测试和风洞试验所存在的物理条件限制，还在很大程度上节约了成本，避免了测试中的危险[3]。随着计算机性能的大幅提高和非定常数值模拟技术的飞速发展，对于飞行器稳定性导数的数值研究，国内外已经开展了大量工作。Zhang Weiwei等[4]采用高效的当地活塞理论对超音速和高超音速下的无粘非定常压力载荷进行了预测；卢学成等[5]将气动力工程算法推广到非定常气动力计算中，求解了任意外形飞行器做强迫振荡运动的非定常气动力，并获得了该飞行器的动导数；刘溢浪等[6]采用基于定常CFD技术的当地活塞理论，发展了一种高效高精度的超音速、高超音速飞行器动导数的计算方法，并通过两个国际标准算例进行了对比验证；A.D.Ronch等[7-8]采用线性频域的谐波平衡法预测了飞行器的周期性非定常流动特性，使计算效率获得大幅提升；David Hassan等[9]采用时域谐波平衡法计算了超音速导弹和民航飞机的俯仰动导数；陈琦等[10]采用谐波平衡法预测了标模导弹的动导数，其计算效率约为双时间推进法的13倍，且在大攻角动态特性计算中取得了令人满意的结果；Scott M.Murman[11-12]采用减缩频率法计算了标模导弹的俯仰动导数；袁先旭等[13]采用CFD方法研究了各种飞行器做俯仰振荡运动的动态特性，并计算了静、动态稳定性导数；范晶晶等[14]采用CFD方法研究了NACA 0012翼型、弹道外形和有翼导弹做强迫俯仰振荡的动态特性。但由于存在计算精度和效率等不足，对于稳定性导数计算问题还需进行深入研究。

本文应用CFD方法中的非结构化动网格技术，模拟飞行器绕横轴做俯仰振荡的整个运动过程；并以国际动导数标模Finner导弹为验证算例，采用多种方法计算Finner导弹在不同马赫数下的俯仰静、动稳定性导数，指出当前工作中的进步与不足，以期为飞行器工程设计工作提供参考。

1　数值方法

1.1控制方程

流场计算采用有限体积法求解时均N-S方程，其积分表达式为

(1)

式中：Q、Fc和Fv分别为守恒变量、对流通量和粘性通量，它们的具体表达式详见参考文献[2]。

湍流模型采用TransitionSST模型，该模型是在SSTk-w的基础上增加了有关间歇度γ和转捩发生准则的两种输运方程，其捕捉流场细节的精度更高。空间离散采用格心格式的有限体积法，时间离散采用隐式离散方法进行双时间推进。

1.2动网格技术

动网格技术可以模拟流场边界随时间变化的问题。网格可根据每次迭代中边界的变化情况自动完成其更新过程。

在任一控制单元中，广义标量Ф的积分守恒方程为

=∫∂VΓΦdA+∫VSΦdV

(2)

式中：ρ为流体密度；u为速度流量；ug为移动网格的网格速度；Γ为扩散系数；SΦ为源项；∂V为控制单元V的边界；A为控制单元的面积。

1.3网格划分与边界条件

网格生成是流场计算的基础，采用ICEM软件对Finner导弹模型进行非结构化网格划分。为了避免边界干扰，远场边界到弹体表面的距离设为弹长的20倍，弹体表面设为无滑移壁面边界。对弹体附近网格进行局部加密以提高计算精度。

2　稳定性导数计算

对于飞行物体，“稳定性”是指其受到扰动之后返回平衡位置的趋势。静稳定性系统不一定具有动稳定性，但动稳定性系统一定具有静稳定性。俯仰力矩是静稳定性导数和动稳定性导数的函数，本文主要讨论俯仰静、动稳定性导数。

2.1理论分析

2.1.1静稳定性导数

俯仰静稳定性导数是当攻角α发生变化时，由于飞行器受到的气动力变化而引起的，也被称为俯仰刚度。其表达式为

(3)

2.1.2动稳定性导数

(4)

(5)

式中：q为俯仰角速度。

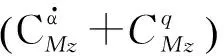
2.1.3俯仰力矩

飞行器作纵向俯仰运动时，若质心速度不变，则在体轴系中的运动独立变量只有攻角和俯仰角速度。假设基准飞行状态为对称直线飞行，且振荡幅度很小，计算中仅考虑一阶动导数，忽略高阶动导数，则将俯仰力矩在初始攻角处作泰勒展开，有

(6)

2.2公式推导

2.2.1静稳定性导数

(1) 差值法

(7)

(2) 直线法

画出力矩系数随攻角变化的迟滞环，找到迟滞环的最左侧点(最小攻角)和最右侧点(最大攻角)，连接这两个点画出一条直线，则该直线必定通过迟滞环的中心，该直线的斜率即为俯仰静稳定性系数，如图1所示。

图1　静稳定性系数示意图Fig.1　Schematic diagram of static stability coefficient

(3) 最小二乘法

该方法将在动稳定性导数计算方法介绍中详细给出。

2.2.2动稳定性导数

(1) 积分法

当刚体飞行器做低频小振幅的俯仰强迫振动时，其强迫振动模型的运动方程为

α=α0+αmsin(ωt)

(8)

式中：α0为初始攻角；αm为振荡幅值；ω为振荡圆频率。

经过简化处理，其模型运动方程可表示为

(9)

将式(9)代入式(6)，合并同类项，可得

(10)

对式(10)沿迟滞环线积分相当于求解非定常气动力做功，即

(11)

由此可得

(12)

对式(12)进行无因次化，得到俯仰组合动导数系数的表达式为

(13)

式中：k为减缩频率，k=ωd/2v。

(2) 最小二乘法

根据式(10)，俯仰力矩还可以表示为

Mz=A+Bsin(ωt)+Ccos(ωt)

(13)

式中：A、B、C为待定系数。

在完成非定常数值计算后，可得俯仰力矩系数随时间变化的曲线，经过无因次化和最小二乘拟合，可求出A、B、C，从而得到静态俯仰力矩系数和俯仰力矩导数。具体表达式为

(14)

(3) 迟滞环法

画出俯仰力矩系数随攻角变化的迟滞环，如图2所示，“+”表示上仰运动，“-”表示下俯运动。

图2　动稳定性系数示意图Fig.2　Schematic diagram of dynamic stability coefficient

大多数导弹的俯仰力矩系数随攻角的变化是准定常的，且环线关于α0中心对称。力和力矩的动稳定性导数可以取导弹在俯仰振荡过程中通过α0时的两点数值来计算，其表达式为

(15)

3　算例与分析

3.1模型与网格

算例选取国际通用的动导数标模Finner导弹[14]，其头部为尖锥形，弹身为圆柱形，尾部带有4个矩形翼，呈“+”形布局，Finner导弹外形示意图如图3所示。

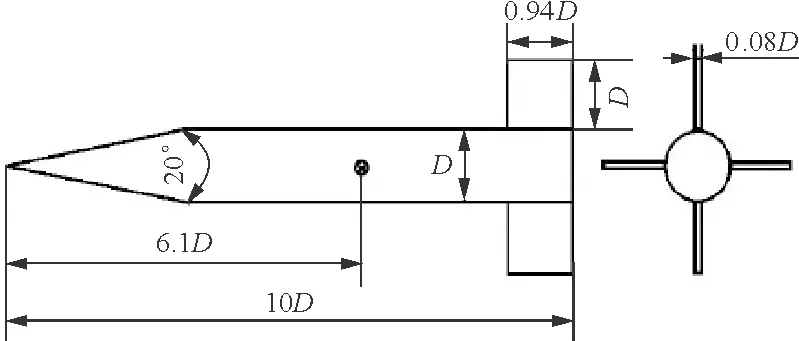
图3　导弹外形示意图Fig.3　Schematic diagram of basic Finnermissile configuration

为了模拟俯仰振荡运动，将计算网格划分为两个域——静域和动域。在非定常计算过程中，模型和动域一起按照指定的形式做俯仰振荡运动，其中，动域网格量为100万，静域网格量为320万。Finner模型网格如图4所示。

(a) 全局网格

(b) 局部网格 图4　Finner模型网格Fig.4　Mesh of Finner model

3.2算例验证

静态计算是动态计算的前提，直接影响动态计算的数值结果。本文首先计算静稳定性导数，当其达到收敛标准之后，再进行动态计算。具体计算工况如表1所示[15]。

表1　计算工况

3.2.1俯仰力矩系数迟滞曲线

马赫数为1.8时，俯仰力矩系数分别随攻角和振荡时间变化的曲线如图5所示。

(a) 俯仰力矩系数随攻角变化曲线

(b) 俯仰力矩系数随振荡时间变化曲线 图5　俯仰力矩系数迟滞曲线(Ma=1.8)Fig.5　Hysteresis curves of pitching momentcoefficient(Ma=1.8)

马赫数为2.7时，俯仰力矩系数随攻角和振荡时间变化的曲线如图6所示。

(a) 俯仰力矩系数随攻角变化曲线

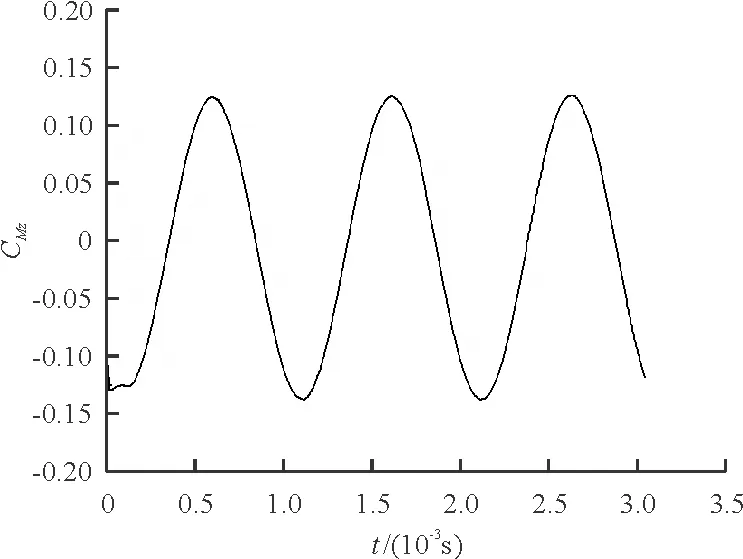
(b) 俯仰力矩系数随振荡时间变化曲线 图6　俯仰力矩系数迟滞曲线(Ma=2.7)Fig.6　Hysteresis curves of pitching momentcoefficient(Ma=2.7)

从图5～图6可以看出：作为攻角的函数，俯仰力矩系数迟滞曲线以(α,CM)=(0,0)为圆心中心对称；作为振荡时间的函数，俯仰力矩系数曲线呈正弦波形式。本文计算结果与文献[15]中Ma为0.9和4.5时的动态曲线趋势一致，规律相符。

3.2.2静导数结果

根据2.2.1节给出的静稳定性导数计算方法，求解俯仰力矩静稳定性导数，计算结果如表2所示。

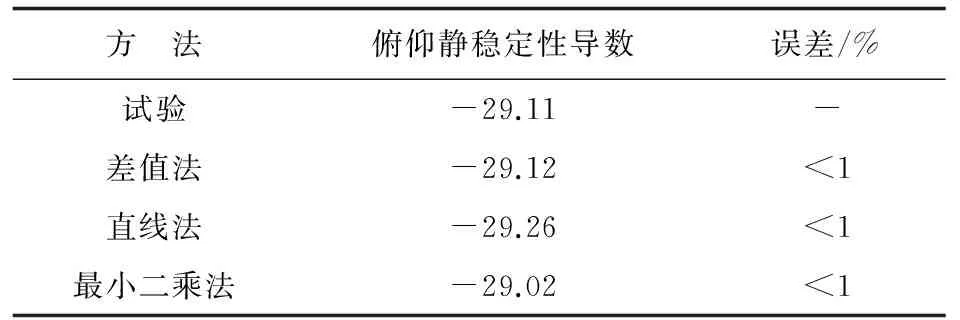
表2　俯仰静稳定性导数(Ma=1.7)

从表2可以看出：采用差值法、直线法和最小二乘法计算出的俯仰静稳定性导数非常接近，在马赫数为1.7时，与试验值的误差均小于1%，表明本文静稳定性导数的计算方法十分可靠。

直线法简便直观，故在后续的计算中，将采用该方法来计算俯仰静稳定性导数。

为了进一步验证静稳定性导数计算结果的正确性，对亚/跨/超三音速下的俯仰静稳定性导数进行计算，如图7所示。

图7　Finner导弹的俯仰力矩静稳定性导数Fig.7　Pitching static stability derivative of Finner missile

从图7可以看出：当马赫数等于1.1时，俯仰静稳定性导数达到最大值；当马赫数小于1.1时，随着马赫数的增加，俯仰静稳定性导数逐渐增大，且静导数随马赫数的变化关系接近于线性；当马赫数大于1.1时，随着马赫数的增加，俯仰静稳定性导数逐渐减小，且趋势变得缓和。与文献[15]的结果相比，本文静导数计算结果与试验值非常接近。

3.2.3动导数结果

根据2.2.2节给出的动稳定性导数计算方法，求解俯仰力矩动稳定性导数，计算结果如表3所示。

表3　俯仰动稳定性导数(Ma=1.83)

从表3可以看出：采用积分法、最小二乘法和迟滞环法计算出的俯仰动稳定性导数非常接近，在马赫数为1.83时，与试验值的误差均小于5.8%，表明本文动稳定性导数的计算方法十分可靠。

为了进一步验证动稳定性导数计算结果的正确性，对亚/跨/超三音速下的俯仰动稳定性导数进行计算，如图8所示。

图8　Finner导弹的俯仰力矩动稳定性导数Fig.8　Pitching dynamic stability derivative ofFinner missile

从图8可以看出：当马赫数小于0.9时，即在亚音速范围内，随着马赫数的增加，动稳定性导数逐渐增大，曲线近似线性，且与文献[15]相比，本文计算结果与试验值更接近；当马赫数大于1.3时，即在超音速范围内，随着马赫数的增加，动稳定性导数逐渐减小，且趋势逐渐变得缓和，与文献[15]相比，本文计算结果的规律性更好，与试验值更接近；当马赫数介于0.9与1.3之间时，即在跨音速范围内，随着马赫数的增加，动稳定性导数先减小后增大，与文献[15]相比，本文计算结果与试验曲线的规律性较一致，取得了较大进步，但数值误差较大，主要原因可能是计算网格密度不够，或者是当前数值方法在计算跨音速时尚存在不足。

在跨音速范围内，本文对俯仰动稳定性导数的计算结果与部分试验值的对比如表4所示。

表4　跨音速范围俯仰动稳定性导数

从表4可以看出：当马赫数等于1.10时，本文数值计算结果与试验值的误差已达21%，主要原因可能是跨音速区域数值方法的计算能力不足，或者是试验结果本身有误。A.B.Vishal等[15]也对试验值提出了质疑，因此本文认为，对于跨音速范围内的俯仰动稳定性导数，应同时开展风洞试验和数值计算来相互验证。

4　结　论

(1) 计算得到的俯仰力矩系数分别随攻角和振荡时间变化的曲线与文献[15]趋势一致，且规律相符，证明了本文数值方法的正确性与合理性。

(2) 计算得到的俯仰静稳定性导数与试验数据非常接近，表明本文关于静导数的计算方法十分可靠。

(3) 在亚音速和超音速范围内，本文关于动稳定性导数的计算结果与试验值更接近，表明本文关于动导数的计算方法十分可靠；而在跨音速范围内，本文的计算结果与试验曲线的规律性较一致，但数值误差较大，主要原因可能是计算网格密度不够，或者是当前数值方法在计算跨音速时尚存在不足，也有可能是试验结果本身有误。

[1]JamesMBrockJr,BruceJolly.ApplicationofcomputationalfluiddynamicsatEglinAirForceBase[R].AIAA-98-5500, 1998.

[2]MichaelEBartowitz.Determinationofstaticanddynamicstabilitycoefficientsusingbeggar[D].Alabama:AirUniversity, 2008.

[3] 李周复. 风洞特种实验技术[M]. 北京: 航空工业出版社, 2010.

LiZhoufu.Specialexperimentaltechniqueinwindtunnel[M].Beijing:AviationIndustryPress, 2010.(inChinese)

[4]ZhangWeiwei,YeZhengyin,ZhangChen’an,etal.Supersonicflutteranalysisbasedonalocalpistontheory[J].AIAAJournal, 2009, 47(10): 2321-2328.

[5] 卢学成, 叶正寅, 张伟伟. 超音速、高超音速飞行器动导数的高效计算方法[J]. 航空计算技术, 2008, 38(3): 28-31.

LuXuecheng,YeZhengyin,ZhangWeiwei.Ahighefficientmethodforcomputingdynamicderivativesofsupersonic/hypersonicaircraft[J].AeronauticalComputingTechnique, 2008, 38(3): 28-31.(inChinese)

[6] 刘溢浪, 张伟伟, 田八林, 等. 一种超音速高超音速动导数的高效计算方法[J]. 西北工业大学学报, 2013, 31(5): 824-828.

LiuYilang,ZhangWeiwei,TianBalin,etal.Effectivelycalculatingsupersonicandhypersonicdynamicderivatives[J].JournalofNorthwesternPolytechnicalUniversity, 2013, 31(5): 824-828.(inChinese)

[7]RonchAD,GhoreyshiM,BadcockKJ,etal.Linearfrequencydomainandharmonicbalancepredictionsofdynamicderitvates[R].AIAA-2010-4699, 2010.

[8]RonchAD,MccrackenAJ,BadcockKJ,etal.Linearfrequencydomainandharmonicbalancepredictionsofdynamicderivatives[J].JournalofAircraft, 2013, 50(3): 694-707.

[9]DavidHassan,FrédéricSicot.Atime-domainharmonicbalancemethodfordynamicderivativespredictions[C].AIAA-2011-1242, 2011.

[10] 陈琦, 陈坚强, 袁先旭, 等. 谐波平衡法在动导数快速预测中的应用研究[J]. 力学学报, 2014, 46(2): 183-190.

ChenQi,ChenJianqiang,YuanXianxu,etal.Applicationofaharmonicbalancemethodinrapidpredictionsofdynamicstabilityderivatives[J].ChineseJournalofTheoreticalandAppliedMechanics, 2014, 46(2): 183-190.(inChinese).

[11]ScottMMurman.Areduced-frequencyapproachforcalculatingdynamicderivatives[C].AIAA-2005-0840, 2005.

[12]ScottMMurman.Reduced-frequencyapproachforcalculatingdynamicderivatives[J].AIAAJournal, 2007, 45(6): 1161-1168.

[13] 袁先旭, 张涵信, 谢昱飞. 基于CFD方法的俯仰静、动导数数值计算[J]. 空气动力学学报, 2005, 23(4): 458-463.

YuanXianxu,ZhangHanxin,XieYufei.Thepitchingstatic/dynamicderivativescomputationbasedonCFDmethods[J].ActaAerodynamicSinica, 2005, 23(4): 458-463.(inChinese)

[14] 范晶晶, 阎超, 李跃军. 飞行器大迎角下俯仰静、动导数的数值计算[J]. 航空学报, 2009, 30(10): 1846-1850.

FanJingjing,YanChao,LiYuejun.Computationofvehiclepitchingstaticanddynamicderivativesathightanglesofattack[J].ActaAeronauticaetAstronauticaSinica, 2009, 30(10): 1846-1850.(inChinese)

[15]VishalAB,JubarajS.Numericalpredictionofpitchdampingstabilityderivativesforfinnedprojectiles[J].JournalofSpacecraftandRockets, 2014, 51(5): 1603-6018.

(编辑：马文静)

Study of Calculating Stability Derivative

Zhang Ruimin， Shi Xiaotian

(The Second Research Institute, China Academy of Aerospace Aerodynamics, Beijing 100074, China)

It is of significant importance to calculate the stability derivative accurately for stability and control of an aircraft. Dynamic mesh technology in computational fluid dynamics(CFD) are used to simulate periodic pitching oscillation motion of Finner missile circling around a fixed axis. The hysteresis curve of pitching moment coefficient for the basic model Finner missile is obtained at different Mach number. The static and dynamic derivatives of the missile in different Mach numbers are computed. The results show that the static derivatives are close to test data very much, and so as the dynamic derivatives in subsonic and supersonic speed range. The results in transonic speed range is of a similar tendency to test data, but with a big error.

stability; derivative; missile; dynamic mesh; pitching oscillation

2016-04-06；

2016-05-18

时晓天,xxtshi@163.com

1674-8190(2016)03-355-07

V211.3

A

10.16615/j.cnki.1674-8190.2016.03.014

张瑞民(1980-)，男，博士，高级工程师。主要研究方向：非定常空气动力学、非线性飞行动力学、飞行器结冰模拟、动力学仿真等。

时晓天(1981-)，男，博士，高级工程师。主要研究方向：空气动力学、计算流体力学。