起落架有限元梁模型建立及其静力学分析

娄锐，折世强，黄海清

(中航飞机起落架有限责任公司 工程技术研究中心，长沙　410200)



起落架有限元梁模型建立及其静力学分析

娄锐，折世强，黄海清

(中航飞机起落架有限责任公司 工程技术研究中心，长沙410200)

为了获得起落架载荷传递以及评估几何非线性和静不定对起落架载荷传递的影响，同时探索起落架结构有限元梁模型的建模方法，应用HyperMesh和Ansys联合仿真的方法搭建某型具有局部静不定特征的前起落架、主起落架有限元梁模型；使用此模型进行三种载荷工况的静力学计算，获得考虑静不定和几何非线性的起落架接头和截面载荷，以及在单位载荷作用下起落架的航向、侧向和扭转刚度，并与传统方法计算结果进行对比。结果表明：有限元方法和传统方法获得的接头载荷有差异，部分差异超过了±10%，最大差异达到30%；计算前起落架外筒横梁、斜梁截面内力的传统方法及其简化具有合理性，对起落架支柱设计具有指导意义。

起落架；有限元梁模型；静不定；几何非线性

0　引　言

获得飞机地面载荷后，根据起落架结构方案，准确计算其载荷传递，包括接头、运动副载荷以及零件截面内力，对起落架设计和优化具有重要意义。虽然起落架是单传力形式，但某些位置存在局部静不定并影响载荷传递，一般的处理方法是对结构做出某种程度的假设和简化，将静不定问题转化为静定问题，从而可以通过平衡方程解算，所获得的载荷是一个近似值。同时，起落架受载发生变形会产生附加弯矩，进一步影响载荷传递，行业规范对外载荷引起变形并对内部载荷分布变化的影响有明确规定[1]。

高泽迥[2]、刘锐琛[3]给出了计算静定起落架结构载荷传递的传统方法，并指出有限元可以解决静不定和变形附加载荷问题，但是并未给出有限元计算载荷传递的建模方法，以及传统方法与有限元方法结果的差异；邵永起[4]研究了考虑起落架结构变形的接头载荷和系统内力的计算方法，但此方法依赖于起落架支柱变形曲线的确定，并指出变形曲线应由梁元素有限元法获得；有限元方法针对起落架的静力学应用局限于零件和装配件的三维实体有限元分析[5-6]，研究目的是获得应力细节，并不是载荷传递和变形模式。

本文针对某型飞机前起落架、主起落架探索建立有限元梁模型，并进行几何非线性静力学分析和应用，包括接头载荷、零件截面内力、初步屈曲分析、刚度随行程的关系，从而获得考虑局部静不定和几何非线性作用的起落架载荷传递规律，并针对传统方法和有限元方法的计算结果进行对比分析，从而获得两种方法对载荷的影响。

1　有限元方法

有限元静力学问题的平衡方程[7]为

KU=Fa

(1)

式中：K为刚度矩阵；U为自由度列阵；Fa为外载荷列阵。

K中元素包含所有静定、静不定结构的刚度，通过求解式(1)可以获得自由度列阵U，根据U计算接头、运动副载荷和截面内力。

在Ansys软件中，几何非线性的求解使用N-R平衡迭代方法，几何非线性的有限元控制方程[8-9]为

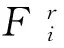
(2)

Ui+1=Ui+ΔUi

(3)

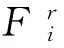
求解过程如下：通过式(2)获得位移增量ΔUi，由式(3)得到新的节点位移Ui+1，式(2)右边称为残余载荷列阵R，当R所规定的范数满足精度要求时，称为载荷收敛，并获得几何非线性问题的收敛解U。

2　起落架结构及计算其结构载荷传递的传统方法

某型飞机前起落架、主起落架结构示意图如图1所示。前起落架主要组成部分如图1(a)所示。支柱和阻力撑杆在航向所形成的三角形用于承受航向载荷，垂向载荷由支柱本身承受，外筒自身侧向的三角形用于承受侧向载荷。

主起落架为上单翼翼根安装的特型起落架，主要组成部分如图1(b)所示。主梁用于连接航向杆、垂向杆和支柱，使三者成为一体，收放支架与机身连接，为了实现支柱的锥面收放，支柱上半部分连接叉形件，叉形件另一端与收放支架相连，为了增加收放支架的侧向刚度，主梁和收放支架之间配置拉杆，下位锁通过锁臂和锁壳之间的插销实现，航向杆和下位锁承受航向载荷，垂向杆和主梁承受垂向载荷，下位锁和主梁承受侧向载荷。

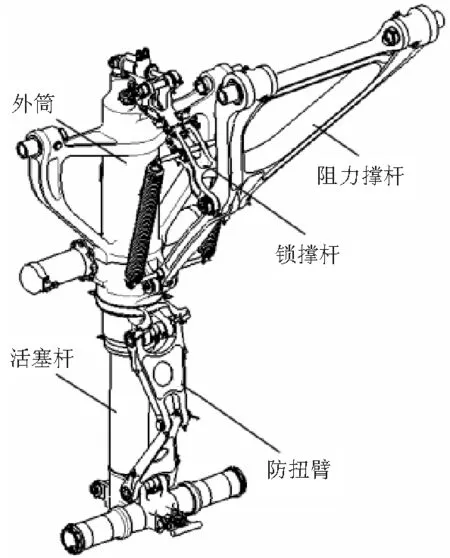
(a) 前起落架

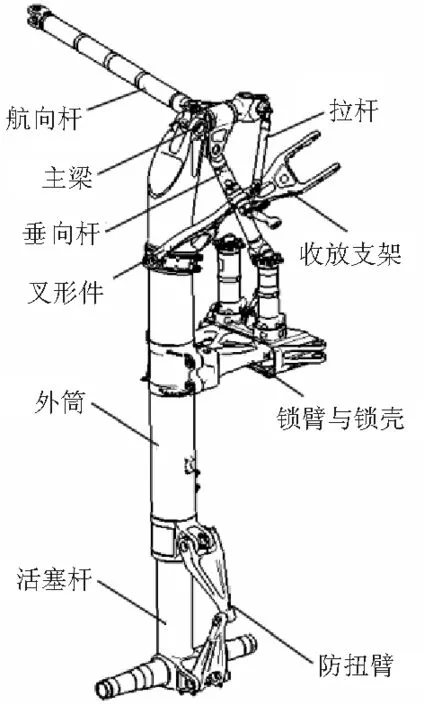
(b) 主起落架 图1　起落架结构示意图Fig.1　Nose and main landing gear structure sketch

前起落架外筒为三角结构，如图2(a)所示。主接头受到Fx、Fy和Fz载荷作用，载荷在外筒横梁和斜梁传递具有静不定特征，传统方法需进行简化和假设，如图2(b)所示。斜梁轴线方向较其他方向刚度大，可简化为二力杆载荷P，横梁与支柱轴线固定连接简化为垂直于三角平面的旋转副，二力杆载荷P由式(4)得到：

P=(Fyd2+Fzd1)/d3

(4)

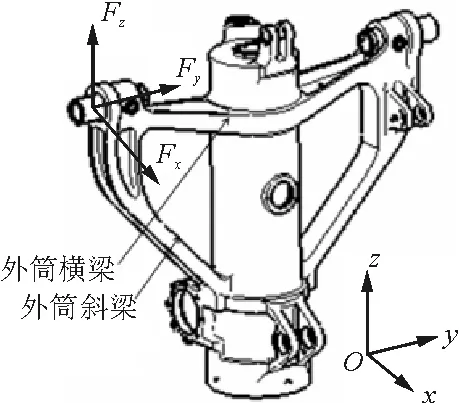
(a) 前起落架外筒接头受力

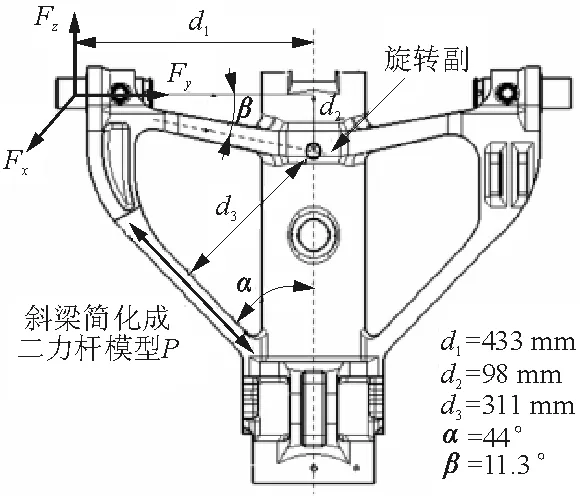
(b) 前起落架外筒横梁、斜梁受载简化 图2　前起落架外筒传力简化示意图Fig.2　Analysis simplification of load path of nose gear main fitting

从图1(b)可以看出：主起落架的主承力结构与叉形件分开布置，叉形件与坐标系的方向余弦全不为零，三个方向都能承受载荷，使得主起落架载荷传递具有静不定特征，传统方法需要进行简化和假设：将叉形件与收放支架断开，同时将主梁与收放支架间的拉杆断开。

主起落架锁销受到的航向载荷Fx1和Fx2通过锁壳传递至接头也是一个局部静不定问题，传统方法将航向载荷在两接头处平分，同时假设侧向载荷Fy1和Fy2在接头处不产生航向载荷，如图3所示。

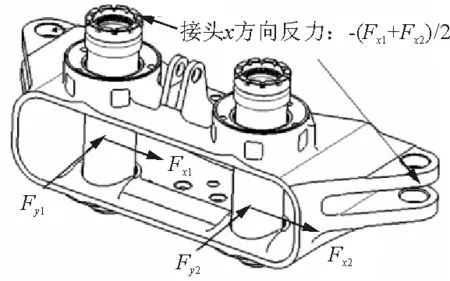
图3　主起落架锁壳受力与边界Fig.3　Force analysis and boundary condition of main gear down lock shell

3　梁模型建立

梁模型坐标系：原点任意，x轴逆航向为正，z轴沿支柱轴线向上为正，右手定则确定y轴。梁模型假设：垂直载荷通过活塞杆完全传递给柱塞再传递给外筒。

应用HyperMesh前处理、Ansys求解的方法进行有限元梁模型的建立和求解[10]。对于具有细长形状的零件，例如活塞杆、柱塞、航向杆应用Beam188梁单元建模，梁单元的刚度由反映结构截面特性的截面数据和材料属性确定；对于具有复杂形状的零件，例如叉形件、锁壳与锁臂则使用Shell281单元建模，壳单元的刚度由其厚度实常数和材料属性确定；梁与梁之间的连接关系通过耦合节点自由度Couple DOF方式实现，活塞杆与下支撑属于此类连接方式；梁与壳的连接方式通过MPC装配技术使用Conta175和Targe170单元并放开相关自由度实现，锁壳与锁销的连接属于该类型，如图4所示，与锁销配合的壳单元节点建立Conta175单元，锁销梁单元节点建立Targe170单元，机轮轮胎使用质量单元Mass21模拟惯量。最后，定义接头位移边界条件，应特别注意前起落架外筒与机身、前起落架上阻力撑杆与机身的侧向约束属于单边约束，通过Conta178单元实现单边约束定义。

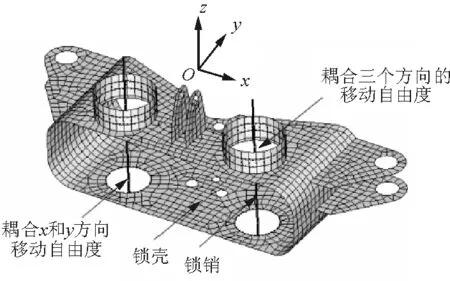
图4　锁壳与锁销的有限元连接模型Fig.4　FEA model of lock shell and pin connection

根据前起落架结构特点，前起落架使用全梁模型进行建模，如图5所示。

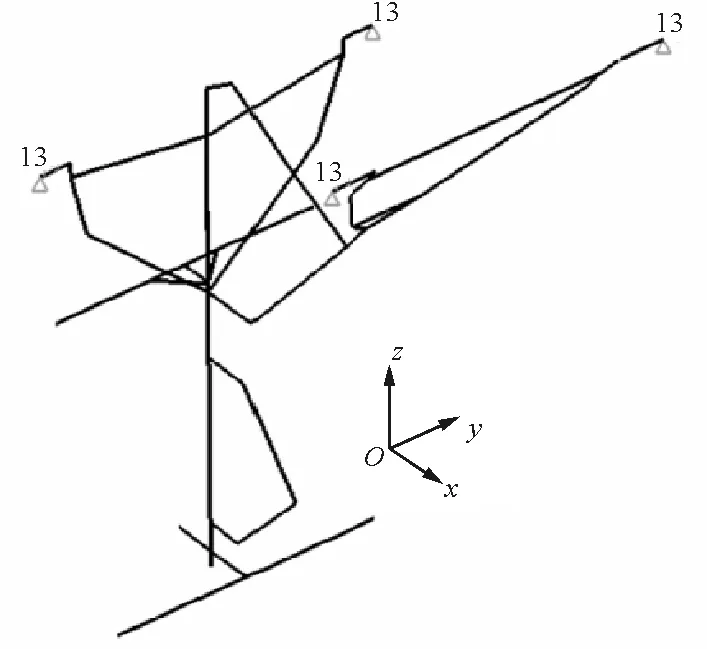
图5　前起落架三维梁模型Fig.5　FEA beam model of nose gear

根据主起落架结构特点，主起落架采用梁壳混合模型，如图6所示。

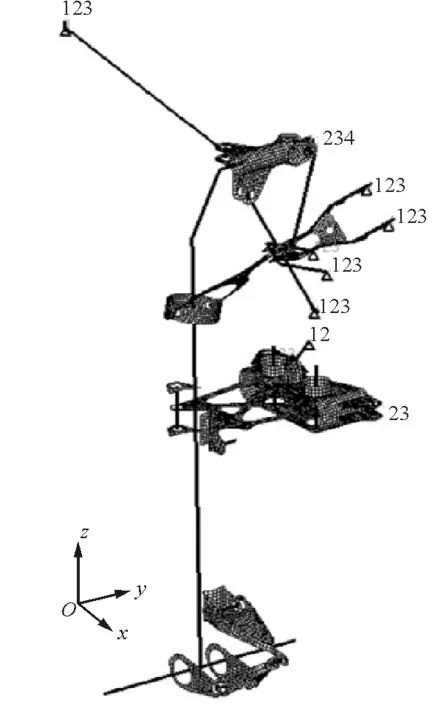
图6　主起落架梁壳模型Fig.6　FEA beam and shell mix model of main gear

4　梁模型静力学应用

获得起落架接头载荷、零件截面内力、运动副载荷以及初步屈曲载荷是计算起落架强度和稳定性的前提，获得起落架轮轴中心航向、侧向和扭转刚度特性是起落架变形计算的前提。

4.1接头载荷

起落架梁模型可以获取考虑局部静不定和几何非线性条件下的接头载荷。以主起落架为对象针对典型工况刹车MB64和转弯MT64(具体载荷情况如表1所示)对接头载荷进行比较，用于对比分析传统方法与有限元方法接头载荷计算结果的差异以及基于有限元方法的几何非线性对接头载荷的影响，计算结果如表2所示。

传统方法接头载荷相对于有限元方法接头载荷的相对变化量如图7所示。由于MT64工况下F2、Fnx、Fmx、Fkx等于0，Fky载荷符号出现反向情况，不参与比较。

基于有限元方法的不考虑几何非线性的接头载荷相对于考虑几何非线性的接头载荷相对变化量如图8所示。由于MT64工况下载荷Fkx较小，不参与比较。

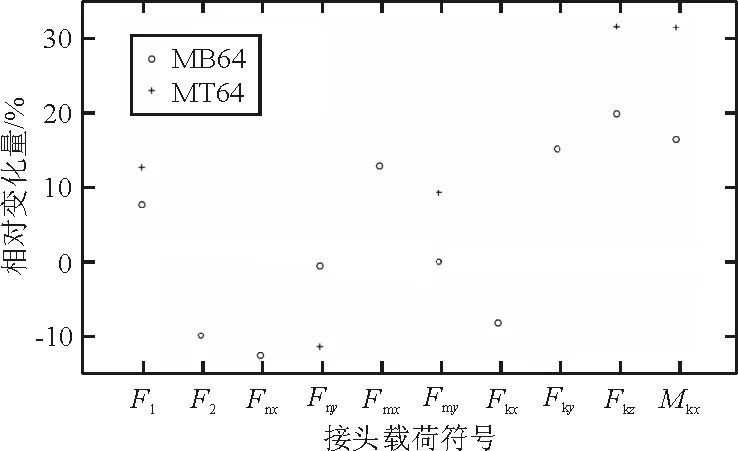
图7　不同工况条件下不同计算方法的 主起落架接头载荷差异Fig.7　Main gear attachment load comparison between different models under different load cases

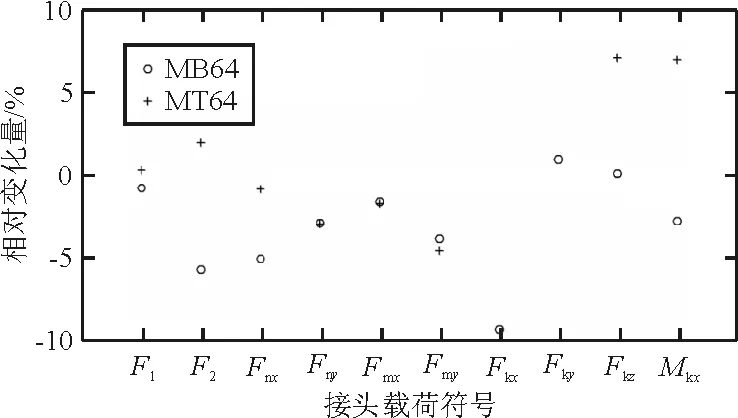
图8　不同工况条件下几何非线性对主起落架 接头载荷影响Fig.8　Geometry nonlinear influence on main gear attachment load under different load cases

从图7可以看出：部分接头载荷差异超过了±10%，最大差异超过30%；大部分接头载荷相对变化量为正，表明叉形件和拉杆承受了一部分地面载荷，起到减载作用；其余接头载荷相对变化量为负，表明几何非线性变形引起的增载超过了静不定的减载。

从图8可以看出：大部分接头载荷相对变化量为负，表明几何非线性对大部分接头载荷起到增加作用；接头载荷差异介于±10%之间；MT64工况下载荷Fky差异达到-73%((6 442-23 903)/23 903×100%)，并考虑到传统方法与有限元方法Fky载荷符号出现反向的情况，表明载荷Fky对侧向地面载荷较敏感。

应注意表2中MT64工况锁壳x方向载荷Fnx和Fmx，因为转弯工况轮轴Plx=Prx=0，所以传统方法Fnx=0、Fmx=0，而有限元方法给出较大互为反向的x方向载荷，这是由于锁壳受到的y方向载荷引起x方向变形引起的。

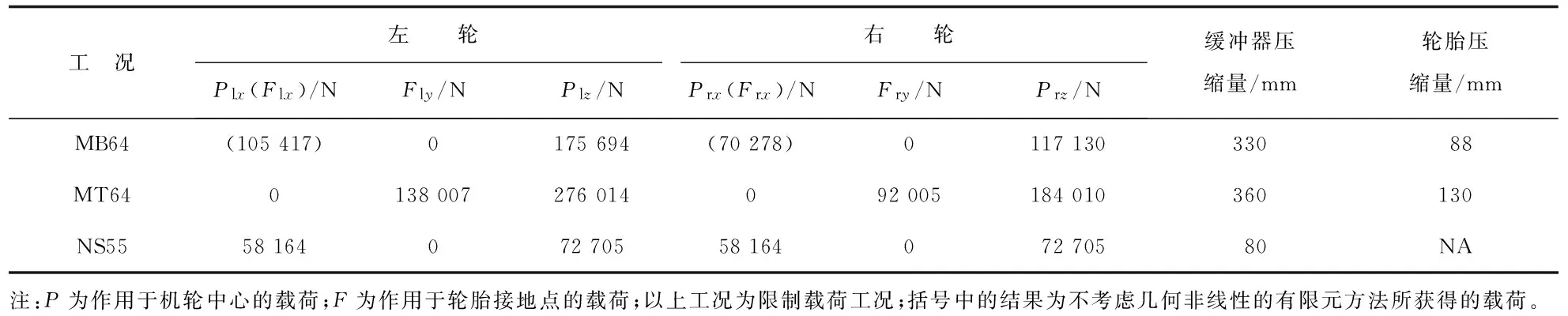
表1　前起落架和主起落架典型工况

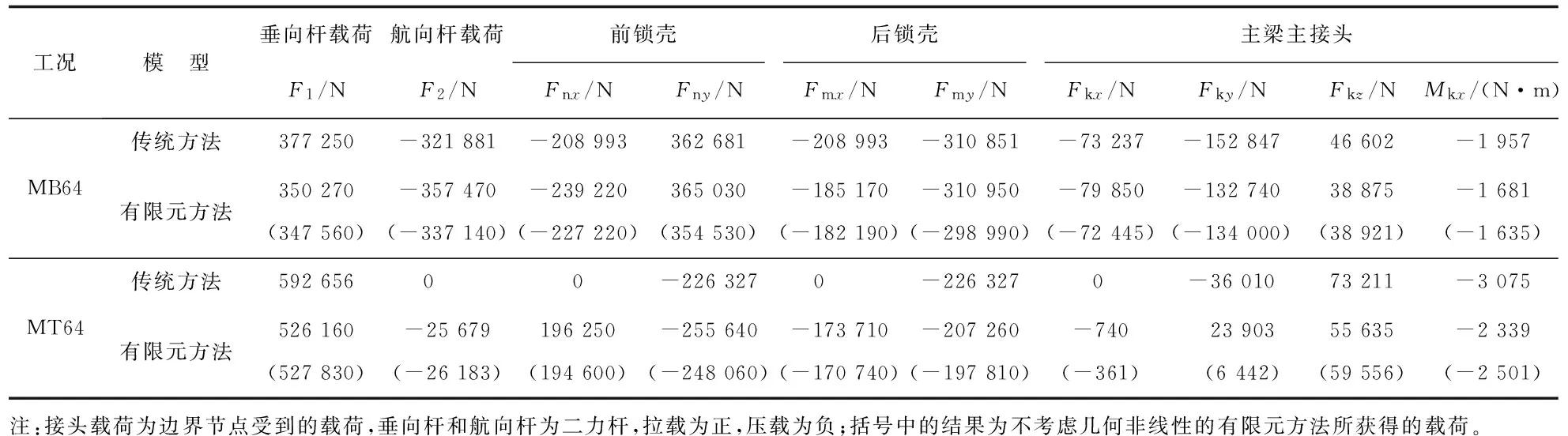
表2　不同工况下、不同计算模型的主起落架接头载荷

4.2截面内力

起落架梁模型可以获取考虑局部静不定和几何非线性条件下的截面内力。针对前起落架典型工况起转NS55，具体载荷情况如表1所示，对外筒横梁、斜梁截面内力进行比较，用于对比传统方法与有限元方法处理局部静不定的截面内力计算结果差异，截面位置如图9所示。根据式(4)，可得传统方法的二力杆载荷P=108 118 N，正号表示二力杆受拉。

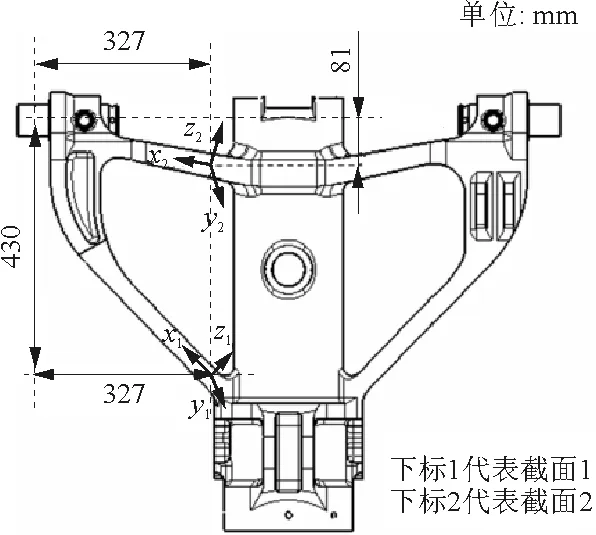
图9　前起落架外筒不同截面位置与截面坐标系Fig.9　Section locations and section coordinate systems of nose gear main fitting

通过输出单元截面内力获得梁模型结果并与传统方法结果比较，如表3所示。

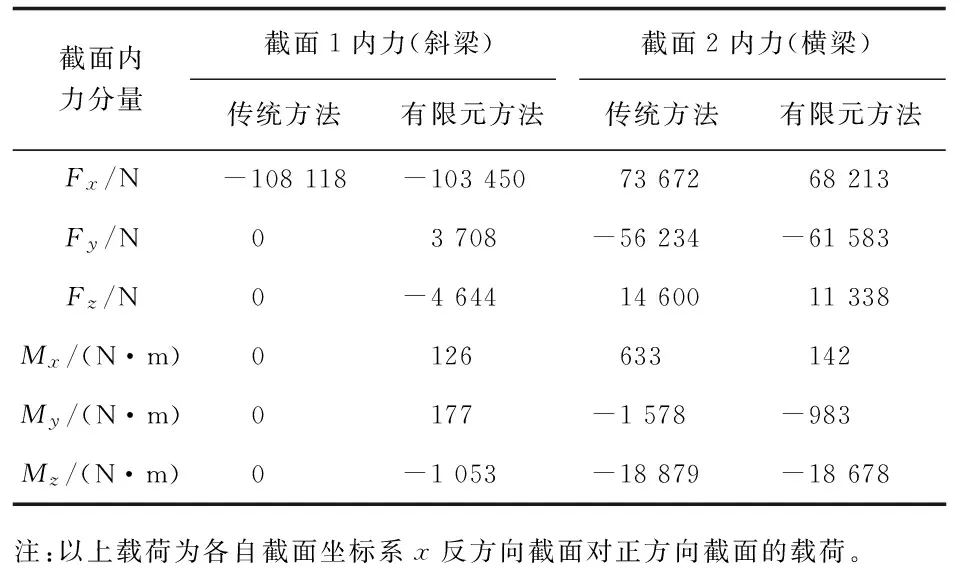
表3　不同计算模型的前起落架外筒不同截面内力

从表3可以看出：传统方法斜梁对于截面1只有轴向载荷Fx，而使用梁模型得出的截面1载荷除了具有较大的轴向载荷外，其余方向还承受了一定的载荷；对于截面1，传统方法和梁模型获得的截面内力在截面设计的主要载荷Fx方面比较一致；对于截面2，传统方法和梁模型获得的截面内力在截面设计的主要载荷Fx、Fy和Mz方面比较一致。因此，计算前起落架外筒横梁、斜梁截面内力的传统方法及其简化具有合理性，对前起落架支柱设计具有指导意义。

4.3运动副载荷

耦合两节点自由度方式形成的运动副，以及MPC装配技术形成的运动副可以通过“节点载荷”获取运动副载荷，本文不展开讨论。

4.4特征值屈曲分析

以主起落架为例，应用主起落架有限元梁模型，进行全局特征屈曲分析[9]，获得载荷因子，为具有较大长细比的受压零件设计提供初步屈曲分析，特征值屈曲分析要求有限元模型是线性的。

在刹车工况MB64下，载荷因子f=2.146 49时的特征屈曲模式如图10所示，为航向杆受压失稳，则在此限制载荷工况下，航向杆受压失稳安全裕度MoS=2.146 49-1=1.146 49，由表2可以获得航向杆受到的压载荷为F2=-337 140 N，则航向杆的受压失稳临界载荷为Fcr=f×F2=2.146 49×(-337 140)=-723 668 N，此载荷可用于航向杆受压临界设计条件。

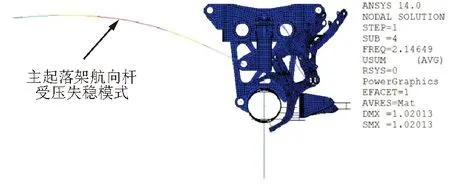
图10　主起落架航向杆失稳模式Fig.10　Longitudinal rod buckling mode of main gear

4.5刚度特性

以主起落架为例，分别建立行程0、0.2和0.4 m的梁模型，各自梁模型分别获得单位载荷Fi作用下对应的变形δi，其中i可以表示航向、侧向和扭转。根据公式Ki=Fi/δi分别计算航向、侧向、扭转刚度，假设刚度是行程的二次函数，再通过二次拟合方法获得全行程的刚度数据，如图11所示。

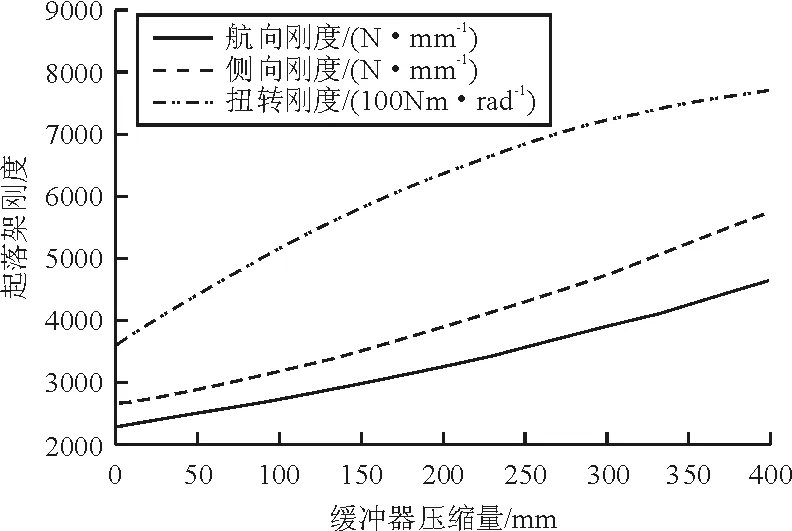
图11　主起落架轮轴中心刚度随行程变化Fig.11　Main gear wheel axle center stiffness vs shock absorber travel

5　结　论

(1) 本文提供了一种新的载荷传递计算方法，所使用的有限元方法在获得起落架载荷传递和整体刚度方面是一种有益的尝试，此方法相对于传统方法考虑了局部静不定和几何非线性条件对载荷传递的影响。

(2) 本文比较了有限元方法和传统方法获得的接头载荷和截面内力，发现对于接头载荷不同方法有较大差异，最大差异达到30%，这对起落架设计和确定零件截面是不利的，建议使用有限元方法获得的载荷用于起落架设计。

(3) 本文提出的有限元方法为仿真计算，计算结果应通过静力试验来验证。

[1] 中国民用航空局. CCAR25-R4-2008运输类飞机适航标准[S]. 北京： 中国民用航空局， 2008： 29.

Civil Aviation Administration of China. CCAR25-R4-2008 Airworthiness standards: transport category airplanes[S]. Beijing: Civil Aviation Administration of China， 2008： 29.(in Chinese)

[2] 高泽迥. 飞机设计手册： 第14分册——起飞着陆系统设计[M]. 北京： 航空工业出版社， 2002： 615-617.

Gao Zejiong. Aircraft Design Manual： Part 14-Take off & landing system design[M]. Beijing： Aviation Industry Press， 2002： 615-617.(in Chinese)

[3] 刘锐琛. 飞机起落架强度设计指南[M]. 成都： 四川科学技术出版社， 1989： 402-403.

Liu Ruichen. Design guides for aircraft landing gear strength[M]. Chengdu： Sichuan Science and Technology Press， 1989： 402-403.(in Chinese)

[4] 邵永起. 起落架弹性变形对结构强度的影响[J]. 飞机设计， 2001(2)： 38-43.

Shao Yongqi. Landing gear elastic deformation impact on structure strength[J]. Aircraft Design， 2001(2)： 38-43.(in Chinese)

[5] 汪洪峰， 汪建利， 宋娓娓， 等. 飞机起落架主起外筒起飞降落过程中的应力分布[J]. 机械设计， 2013， 30(6)： 61-64.

Wang Hongfeng，Wang Jianli，Song Weiwei，et al. Stress distribution of main outer cylinder of landing gear in process of aircraft tanking off and landing[J]. Journal of Machine Design， 2013， 30(6)： 61-64.(in Chinese)

[6] 黄铭敏， 左敦稳， 黎向锋， 等. 四轮并式起落架焊接主起轮轴受载模型及分析[J]. 中国机械工程， 2012， 23(17)： 2071-2074.

Huang Mingmin， Zuo Dunwen， Li Xiangfeng， et al. Model establish and numerical analysis of welded wheel axle of four-wheel-juxtaposed landing gear[J]. China Mechanical Engineering， 2012， 23(17)： 2071-2074.(in Chinese)

[7] 曾攀. 有限元分析及应用[M]. 北京： 清华大学出版社， 2004： 96-98.

Zeng Pan. Finite element analysis and applications[M]. Beijing： Tsinghua University Press， 2004： 96-98.(in Chinese)

[8] 王新敏. 杆系结构的几何非线性分析综述[J]. 石家庄铁道学院学报， 1993， 6(3)： 80-84.

Wang Xinmin. On the geometric nonlinear analysis theory of frames[J]. Journal of Shijiazhuang Railway Institute， 1993， 6(3)： 80-84.(in Chinese)

[9] Ansys. Ansys help[M]. USA： Ansys company， 2013.

[10] 贺李平， 龙凯， 肖介平， 等. ANSYS 13.0与Hyper Mesh 11.0联合仿真有限元分析[M]. 北京： 机械工业出版社， 2012： 39-51.

He Liping， Long Kai， Xiao Jieping， et al. ANSYS 13.0 and Hyper Mesh 11.0 cosimulation of finite element analysis[M]. Beijing： China Machine Press， 2012： 39-51.(in Chinese)

(编辑：马文静)

Establishing FEA Beam Model of Landing Gear and Its Analysis of Statics

Lou Rui, She Shiqiang, Huang Haiqing

(Engineering Technology Research Center， AVIC Landing Gear Advanced Manufacturing Corporation， Ltd.， Changsha 410200， China)

In order to obtain load path of landing gear and evaluate the load path impact of geometry nonlinear and static indeterminacy, meanwhile to explore method of building FEA beam model of landing gear, the FEA beam models of specific type nose and main landing gear with feature of local static indeterminacy are built by way of HyperMesh and Ansys co-simulation. Static calculation of three load cases is conducted using the FEA model. The joint load and section load of landing gear with feature of static indeterminacy and geometry nonlinear are obtained, and longitudinal, lateral and torsion stiffness of the gear are obtained under unit load, and compared with that by using the traditional method. Results show that there is difference between the joint load of the two methods. Some difference is exceeded by ±10% and the biggest difference achieved by 30%. The traditional method and simplification of calculating section load of level beam and inclined beam of nose strut is reasonable and is of guidance meaning in designing nose strut.

landing gear; finite element beam model; static indeterminacy; geometry nonlinear

2016-06-04；

2016-07-23

娄锐,lourui607@163.com

1674-8190(2016)03-325-07

V226

A

10.16615/j.cnki.1674-8190.2016.03.009

娄锐(1985-)，男，硕士，工程师。主要研究方向：起落架缓冲性能和载荷分析。

折世强(1968-)，男，研究员。主要研究方向：起落架缓冲性能和载荷分析。

黄海清(1975-)，男，高级工程师。主要研究方向：起落架强度计算与设计。