加权马尔科夫链对汛期降水量的预测

王志刚

（辽宁省大连水文局，辽宁 大连 116023）

加权马尔科夫链对汛期降水量的预测

王志刚

（辽宁省大连水文局，辽宁 大连 116023）

根据碧流河水库坝址以上1958至2002年汛期的流域平均降水量，利用加权马尔科夫链法对2003—2005年汛期降水量进行预测，与实测结果相比，3年汛期降水量均在预测允许范围之内，计算方法简便，预测结果较准确，对水库调度有着重要意义。

汛期降水量；加权马尔科夫链；预测；碧流河水库

1 概述

碧流河水库是大连市的水源地，根据水库统计多年平均降水量、径流量资料分析得知，汛期降水量占全年降水量的75%左右，汛期的径流量占全年径流量85%左右，降水是形成径流的主要因素，因此较准地确预测未来汛期降水量对水库的蓄水、供水等有着十分重要的意义。

由于降水受到很多因素的影响，并且有很大的随机性，通常难以通过物理成因对未来某一时段的降水量进行准确数值预测。在现实工作中，如果能预测出未来时段降水量变化区间那么也就大大提高了预报的精度。预测范围增大了，预报的可靠性也就提高了。对大量的降水序列资料统计分析及物理成因的定性分析得知，降水量为一相依随机变量，其相依关系的强弱通常采用自相关系数作为其定量的测度，因此对降水量丰枯状况划分变化区间，用加权马尔可夫链对碧流河水库汛期的降水量丰枯变化进行预测。

2 马尔科夫链与加权马尔科夫链预测计算步骤

2.1 马尔科夫链

马尔科夫链是时间和状态都离散的马尔科夫过程，其数学表达式如下：定义在概率空间（赘，F，P）上的随机序列{X（t），t∈T}，其中参数集 T= {0，1，2，…}，状态空间 E={0，1，2，…}，称为马尔科夫链，如果对任意的正整数l，m，k，及任意的非负整数jl>…>j2>j1（m>jl），im+k，im，ijl，…ij2，ij1∈E有式（1）成立（这里要求式（1）的左端有意义）。

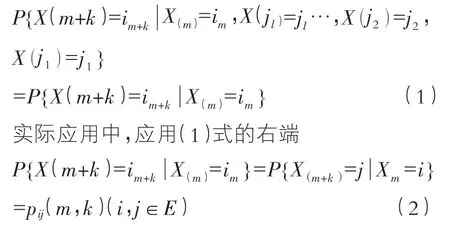
在现实应用中，一般考虑齐次马尔科夫链，即对任意的m，k∈T，pij（m，k）=pij（k）（i，j∈E）。

其中pij（m，k）表示为系统在时刻m时处在状态i、经k步状态转移到达状态j的概率；pij（k）为系统从状态i、经k步状态转移j的概率，此时转移概率与初始时刻无关，k=1时pij（1）记为pij。

齐次的马尔科夫链{X（t）}完全由初始分布{p（i），i= 0，1，…}及其状态转移概率矩阵（状态转移概率pij，（i，j=0，1，…）所构成的矩阵）所决定。

2.2 加权马尔科夫链模型具体计算步骤

2）建立汛期降水量的分级标准，将汛期降水量分成干旱、偏旱、正常、偏丰、丰水5个状态。

3）对第二步所得到的状态结果进行统计，能够得到不同滞时（步长从1至5）的一步转移概率矩阵。

4）对汛期降水量序列的各阶自相关系数rk进行计算：

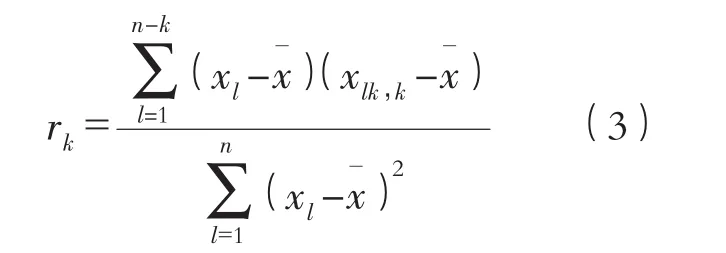
式中：rk为第k阶（滞时为k）的自相关系数；xl为第l时段的汛期降水量；x为汛期降水量均值；n为汛期降水量的长度。

5）各阶自相关系数wk实行规范化，即：

式中：wk为规范化相关系数；m为预测需要计算的最大阶数。

6）分别以前面各时段的汛期降水量作为初始状态，结合其相应的各阶转移概率矩阵，可预测出这个时汛期降水量的状态概率。

7）对同一状态的各预测概率pi加权和，作为降水量处于这种状态的预测概率：

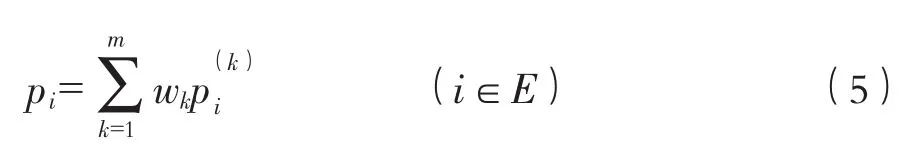
max｛pi，i∈k｝为这个时段降水量的预测状态,这个时段降水量发生后，加入到原序列，然后重复从1至7的计算步骤，进行下一年的汛期降水量状态的预测。

3 利用加权马尔科夫链预测碧流河水库汛期降水量

本文以碧流河水库站统计1958—2005年汛期降水量资料（降水量资料摘自碧流河水库调度手册，手册降水量资料只统计到2005年），首先用1958—2002年的汛期降水量资料，预测2003年汛期降水量，把2003年汛期降水量加入到原序列，再预测2004年汛期降水量，把2004年汛期降水量加入到原序列，最后预测2005年汛期降水量。

1）首先计算碧流河水库从1958—2002年汛期流域平均降水量均值x=548.6 mm、标准差滓= 153.8 mm。

2）按照表2所建立的标准确定资料序列中各时段所对应的状态。

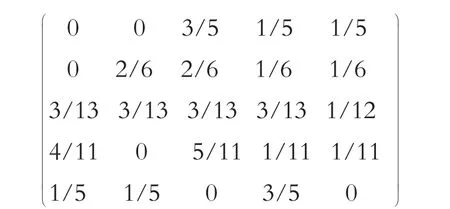
3）计算步长从1～5状态转移概率矩阵：

表1 碧流河水库1958—2002年汛期降水量序列及状态表

表2 碧流河水库汛期降水量分级表

①步长为1状态转移概率矩阵：

②步长为2状态转移概率矩阵：

③步长为3状态转移概率矩阵：

④步长为4状态转移概率矩阵：

⑤步长为5状态转移概率矩阵：

4）按照公式（3），计算各阶自相关系数，r1= -0.116，r2=0.232，r3=0.051，r4=-0.057，r5=-0.194。

5）按公式（4），对各阶自相关系数进行规范化，w1=0.194 8，w2=0.390 6，w3=0.024 9，w4=0.096 6，w5=0.293 0。

6）根据1998—2002年状态转移概率矩阵，乘各阶自相关系数， max{pi}=0.282 4（见表 3），i=1，预测2003年汛期为枯水年，x<379.5，2003年实测值359.9 mm。

把2003年汛期降水量加入到序列，以1958—2003年汛期降水量序列，重复上述计算步骤，预测2004 年汛期降水量，max{pi}=0.448 2，i=3，预测2004年汛期为正常年份，降水量467.2≤x<621.8，2004年实测值592.9 mm。同理，把2004年汛期降水量加入到序列，以1958—2004汛期降水量序列，重复上述步骤，预测2005年汛期降水量，max{pi}= 0.433 3，i=3，预测2005年汛期为正常年份，降水量469.0≤x<622.1，2005年实测值474.2 mm。（预测2004年、2005年汛期降水量具体计算步骤略）

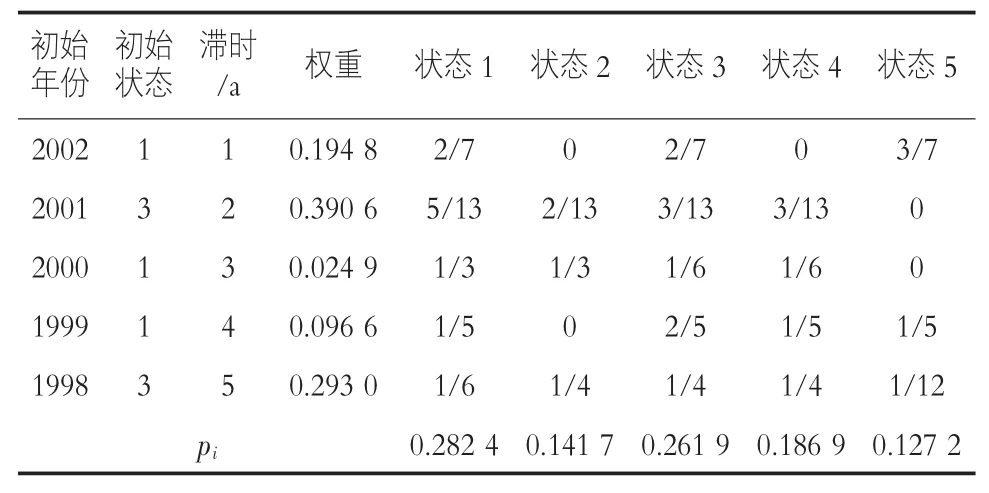
表3 碧流河水库2003年汛期降水量状态预测表

4 结 语

1）因为以各种步长的自相关系数为权重，以各种步长的马尔科夫链加权和来预测降水量状态，与叠加马尔科夫链预测方法相比较，能更充分、合理地利用信息，可以将马尔科夫链与相关分析结合起来进行预测。

2）预测结果为降水量是一个区间值，而不是一个点值，在满足工作的前提下，预测的范围扩大了，预报精度也随之提高。

3）随着预报系列的增长，资料的代表性也会日益增强，应将每年预报对象的新的实测值加入到分析的系列，计算预报对象的自相关系数、状态转移矩阵概率、权重，可以进一步提高预报精度。

4）本文应用加权马尔可夫链预测的是汛期降水量，还可以用加权马尔可夫链来预测单月降水量或旬降水量。

5）应用加权马尔可夫链对碧流河水库汛期降水量的预测，计算方法简便，预测结果比较准确，对于水库调度有着重要的意义。

［1］夏乐天，朱元生生，等.加权马尔科夫链在降水状况中的应用［J］.水利水电科技进展，2006，26（6）：20-27.

TV125；P338+.1

A

1002－0624（2016）04－0036－03

2015-12-09