M—DSP中高性能浮点乘加器的设计与实现
车文博 刘衡竹 田甜

摘要:针对高性能M型数字信号处理器(M-DSP)对浮点运算的性能、面积和功耗要求,研究分析了M-DSP总体结构和浮点运算的指令特点,设计和实现了一种高性能低功耗的浮点乘累加器(FMAC)。该乘加器采用单、双精度通路分离的主体结构,分为六级流水站执行,对乘法器、对阶移位等关键模块进行了复用设计,支持双精度和单精度浮点乘法、乘累加、乘累减、单精度点积和复数运算。对所设计的乘加器进行了全面的验证,基于45nm工艺采用Synopsys公司的Design Compiler工具综合所设计的代码,综合结果表明运行频率可达1GHz,单元面积36856μm2;与FT-XDSP中的乘加器相比,面积节省了12.95%,关键路径长度减少了2.17%。
关键词:浮点乘法;浮点乘累加器;浮点点积;布斯算法;IEEE754
中图分类号:TP332.2
文献标志码:A
0引言
数字信号处理器(Digital Signal Processor, DSP)从专用信号处理器开始发展到今天的超长指令字(Very Long Instruction Word, VLIW)阵列处理器,其应用领域已经从最初的语音、声纳等低频信号的处理发展到今天雷达、图像等视频大数据量的信号处理。由于浮点运算和并行处理技术的应用,信号处理能力已得到极大的提高。随着数字信号处理器在处理速度和运算精度两个方向的发展,体系结构中数据流结构甚至人工神经网络结构等,将可能成为下一代数字信号处理器的基本结构模式。近些年,从传统DSP结构中已不能有效地提高DSP处理器的性能,许多新的提高DSP性能的方法被提出[1]。其中提高频率的方法已达到瓶颈阶段,最有效的途径是提高并行性。数字信号处理领域的核心算法根据运算类型可以分为两大类:一类是以密集的浮点乘加运算为典型的信号处理算法,包括快速傅里叶变换(Fast Fourier Transformation, FFT)[2-3]、有限冲激响应(Finite Impulse Response,FIR)和离散傅里叶变换(Discrete Fourier Transform, DFT)等算法;另一类是以密集的复数矩阵操作为主的算法,包括信道估计和多输入多输出(Multiple-Input Multiple-Output, MIMO)均衡[4]等算法。这两类算法均需要DSP处理器提供较高的浮点乘加运算的计算性能。第一类算法主要是进行乘加运算(a*b+c),第二类算法主要进行大量的复数矩阵乘和矩阵求逆等运算,而在这些运算中都存在密集的乘后加运算(a*c+c*d)。浮点乘累加器(Floating-point Multiply ACcumulate, FMAC)已经成为提高并行计算以减少计算延时的有效方法,其运算能力已经成为衡量数字信号处理器DSP性能的一个重要特征。
浮点乘加结构已被研究多年,IBM学者Montoye和Hokenek于1990年最先提出了融合乘加的概念[5],即将乘法和加法融合成一条指令执行,并将加法操作融合在乘法的部分积压缩阵列中,从而减少硬件开销和延时;这种乘加结构的主要缺点是求和尾数长且结果尾数舍入延时长。Lang等[6]于2004年提出了低延时融合乘加结构,这种结构采用前导零预测(Leading Zero Anticipation, LZA),将尾数舍入和加法合并,并在尾数加法之前进行规格化移位。目前大多数处理器中的浮点乘加设计实现均采用这种技术,为进一步提高浮点融合乘加结构的并行度以提升浮点乘加器的性能,Lang等[7]于2005 年设计了双通路浮点融合乘加结构,该乘加结构主要优点是延时更低、处理性能得到进一步提高;但该乘加结构逻辑设计复杂,硬件资源消耗大。国防科技大学研制的FT-XDSP中设计了多功能快速浮点融合乘加运算单元[8],但该设计硬件资源消耗太多,功耗过大。
本文基于高性能计算的应用需求,以M型数字信号处理器(M-DSP)为研究背景,深入研究FMAC的各功能模块和流水线结构,对已有浮点融合乘加结构[9]的关键模块和算法进行了研究与优化,设计了6级流水线结构的FMAC单元,可支持双精度和单精度浮点乘法、乘累加、乘累减、单精度点积和复数运算。对所设计的FMAC单元的寄存器传送语言(Register Transfer Language, RTL)代码实现进行了仿真测试,并基于45nm工艺采用Synopsys公司的DC(Design Compiler)对硬件实现进行了综合,运行频率可达1GHz。
1M-DSP处理器体系结构
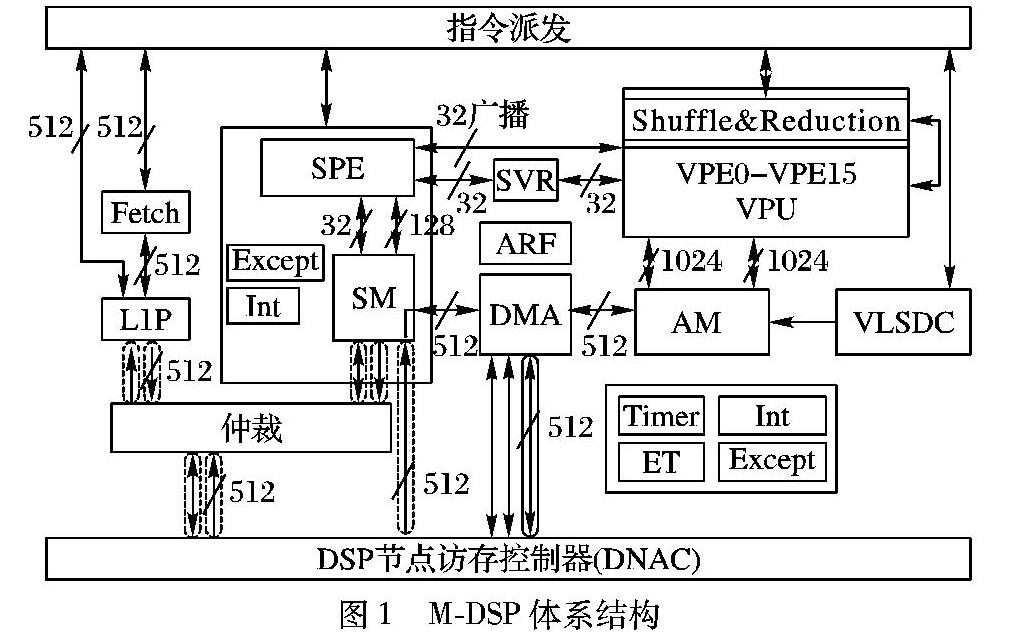
M-DSP总体结构设计如图1所示。M-DSP 是自主研发的一款具有自主知识产权的高性能DSP,目标频率1GHz。内核采用新型的哈佛结构,采用可变长的11发射超长指令字结构,可以同时并行取指和派发11条指令。M-DSP中内核结构主要包括一级程序Cache、取指单元(Instruction Fetch, IF)、指令派发单元(DisPatch, DP)、向量运算部件(Vector Process Unit,VPU)、标量运算部件(Scale Process Unit,SPU)和向量阵列存储器(Array Memory, AM)等。其中运算部件是DSP内核中最重要的单元之一,约80%以上的指令来自于运算部件。标量运算单元(Scale Process Element, SPE)包括两个乘加部件和一个定点执行单元。两个同构的乘加部件由共享54×32位乘法器结构的定点MAC单元与浮点MAC单元以及浮点算数逻辑单元(Arithmetic Logical Unit, ALU)组成,三个单元独立运算但共用乘累加(Multiply-ACcumulate, MAC)单元的写端口写回到寄存器,三个单元共用同一套寄存器端口。
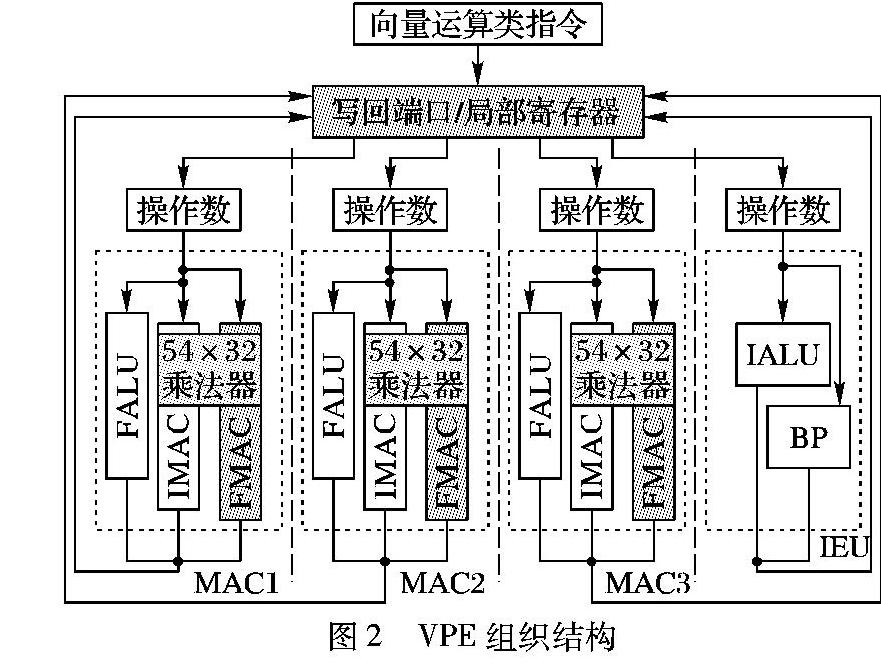
向量运算单元(Vector Process Element, VPE)内数据通路如图2所示,它包含64个局部通用寄存器,三个同构的MAC部件由定点乘加(Integer Multiply Accumulate, IMAC)、浮点MAC和浮点ALU单元三个单元构成,其中FMAC和IMAC复用了一个54×32乘法器。向量运算部件均包含有16个相同结构的向量运算单元VPE,与标量运算类似,每一个向量运算单元由三个向量乘加部件(Vector Multiply ACcumulate, VMAC)及一个向量定点执行单元组成。每一个单元内部的部件组成及数据写回方式与标量的处理方式相同。
VPE之间通过混洗网络和规约树网络进行数据交互。混洗网络可以根据混洗粒度和混洗模式的不同对VPE之间的数据进行混洗操作;归约网络将多个VPE中的数据通过多宽度规约方式规约到一个或者多个VPE中,多宽度归约操作将所有的16个VPE进行分组,每个分组归约操作并行执行,分组只支持平均分组,分组大小为2的整数次幂。
2FMAC单元的结构设计与实现
2.1浮点乘加单元指令集设计
浮点MAC单元共设计实现9条指令(如表1所示),包括双精度乘法(Double Floating-point MULtiply, DFMUL)、单精度乘法(Single Floating-point MULtiply, SFMUL)、双精度乘加(Double Floating-point MULtiply-Adder, DFMULA)、单精度乘加(Single Floating-point MULtiply-Adder, SFMULA)、双精度乘减(Double Floating-point MULtiply-Subtration, DFMULS)、单精度乘减(Single Floating-point MULtiply-Subtration, SFMULS)、浮点复数实部乘法(Floating-point Complex multiplication REAL, FCREAL)、浮点复数虚部乘法(Floating-point Complex multiplication IMAGinary, FCIMAG)和
浮点点积(Floating-point DOT product, FDOT)指令。由于寄存器端口的限制,双精度指令和4操作数单精度指令需要读取两拍,双精度结果写回需要两拍。
2.2高性能浮点MAC单元的体系结构设计
浮点MAC单元其总体结构设计实现如图3所示。基于经典低延时浮点乘加结构,根据M-DSP的体系结构设计要求设计实现了双精度浮点乘加运算通路,在此基础上复用部分硬件实现单精度指令的相关运算通路,包括单精度浮点乘法/乘加、点积和复数操作。为提高性能、降低逻辑设计复杂度,基于传统浮点乘加结构将单、双精度指令计算分开处理,设计了一套单、双精度通路分离[10]的浮点乘加结构。所设计的浮点MAC单元包括54×32共享乘法器、指数计算、源操作数例外判断、尾数对阶移位、尾数加法、乘法结果输出、结果符号计算、结果尾数规格化移位、结果舍入和结果选择写回等模块,单/双精度浮点操作均需要用到上述模块。根据逻辑复用的设计思想,将对阶移位、尾数加法和前导零等模块进行优化,使得硬件逻辑在支持单/双精度浮点乘加的同时支持单精度浮点乘法后加法操作。各流水线设计如下:
1)流水线第一站设计实现。流水线第一站主要由源操作数读取、源操作数例外判断、指数计算和对阶移位量计算等运算模块构成(乘法器模块单独设计),其中乘法器的相关模块与定点MAC单元共用,为了减少乘法器面积和提高逻辑复用的能力,采用4个27×16的乘法器实现54×32的乘法操作,双精度乘法需要两次乘法操作才能计算出结果,乘法器详细设计在2.3.1节中介绍。
2)流水线第二站设计实现。流水线第二站主要包括部分积压缩第3级、27×16乘法结果的Sum与Carry的加法和乘法/乘加指令的尾数对阶移位等运算模块。第3级部分级压缩将乘法器中前两级压缩的结果采用进位保留加法器(Carry-Save Adder, CSA)进一步压缩,在得到单精度乘法的部分积和阵列的Sum和Carry后,采用43位加法器对Sum和Carry进行全加操作,得到高位部分的单精度浮点乘法结果尾数。
3)流水线第三站设计实现。流水线第三站包括乘加/乘后加指令的尾数加法等运算模块。在第三站中,在单精度乘法操作完成后,双精度乘法的中间结果Sum和Carry也已计算出来,采用2个全加器用来计算浮点尾数求和,前导零LZA逻辑有部分逻辑在第三站进行。
4)流水线第四站设计实现。第四流水站主要包括前导零预测LZA第二部分、乘加结果尾数舍入进位处理、乘法结果溢出、例外判断和乘法结果选择写回等运算模块,在乘法结果旁路写回模块中,单精度乘法执行4拍写回,双精度乘法由于读、写都要多一拍,需要6拍写回结果。
5)流水线第五站设计实现。流水线第五站主要包括规格化移位、尾数舍入处理、结果符号计算和结果指数修正。在第五级流水线中,浮点MAC除乘法类的各条指令的规格化移位都使用128位对数移位器对结果尾数进行规格化移位。根据舍入模式以及粘接位的值,舍入模块判断是否对最后结果尾数进行加1操作。根据规格化移位的结果尾数和移位量,利用指数修正模块可以计算出正确的结果指数,根据尾数加法的最后结果采用符号计算逻辑判断结果符号。
6)流水线第六站设计实现。第六级流水线主要包括结果尾数的例外判断、溢出判断以及结果选择写回处理。结果尾数选择写回时,先根据浮点控制寄存器中各标志位进行结果处理,待结果尾数确定后选择写回,写回时双精度指令要写两拍。
2.3浮点MAC单元关键模块设计
2.3.1乘法器设计
传统的定点和浮点运算部件都有单独的乘法器单元。特别是处于同一流水线上的定、浮点单元,这样的设计会导致硬件资源浪费。因此在M-DSP中,采用定点乘加部件与浮点乘加部件复用同一个乘法器,这样可以在满足功能要求的前提条件下,提高硬件利用率,减少芯片面积。按照指令设计需求,定点MAC单元中有32×32和单指令多数据(Single Instruction Multiple Data, SIMD)的16×16定点乘法,浮点MAC单元有54×54和24×24的浮点乘法。由于寄存器文件端口个数和位宽的限制,浮点乘加的读操作数与写结果均需要两拍实现,无法实现全流水操作。通过优化逻辑结构,因此将乘法器设计为54×32位乘法器,采用4个27×16的子乘法器搭建而成,复用的乘法器共三级流水,其中定点MAC单元使用前面的两级流水站,浮点MAC单元使用三级流水站。由于乘法器面积在定、浮点乘加部件面积中比重较大,共享同一个乘法器的设计可以大幅度减少MAC单元的面积。
27×16位乘法器采用两级流水实现,其实现结构如图4所示,其中基2Booth编码[11]、第一级压缩与第二级压缩为第一站,第三级压缩和Sum与Carry的加法为第二站。这样的流水设计满足功能要求和时序要求,并且可以提高乘法器速度。对所设计的27×16位与54×32位乘法器进行模块级验证后,使用综合工具DC在40nm工艺下对所设计的乘法器进行了逻辑综合, 27×16位乘法器关键路径340ps,单元面积6758.707μm2,单元总功耗6.0817mW;54×32位乘法器关键路径390ps,单元面积27438.196μm2,单元总功耗17.4217mW。
定、浮点MAC单元共享乘法器结构如图5所示,其中PP0~PP8表示9个部分积(Part of the Product, PP),乘法器内部有单独的源操作数预处理模块,根据派发的定、浮点指令对读取的源操作数进行处理,浮点尾数乘法的操作数均视作无符号数,而定点的操作数则要区分有无符号分别处理。
2.3.2对阶移位和规格化移位
本文所设计的浮点乘加单元,浮点乘加指令需要对尾数进行对阶移位,设计一个m位移位器,将尾数乘积固定在设计的移位器最右端,通过固定右移加数实现对阶。乘积与加数的指数差决定了对阶移位的移位量。同样在进行乘加/减指令时,在对尾数进行加法后,由于尾数高位可能会出现0的情况,为满足IEEE754浮点数标准,需要对结果尾数进行规格化,使其最高位为1,即规格化移位,在规格化的同时根据移位量对预测结果指数进行修正。本文所设计的浮点MAC单元,除乘法类指令外其余指令需要进行规格化移位操作。
在浮点MAC 中设计了两个右移的对阶移位器,一个是106位用于单/双精度浮点乘加尾数对阶移位器,一个是98位用于点积和复数指令运算的对阶移位器,均处于浮点MAC流水线上的第二级流水站。设计两个对阶移位器主要是考虑时序问题,通过实验,复用同一个对阶移位器时,面积并没有减少,由于关键路径的增加,面积还会有增大。这里以点积指令为例介绍其移位设计思想。浮点单精度点积乘法尾数对阶采用一个98位的移位器进行对阶操作, 98位移位器的结构组成是由48位单精度乘法结果、用于保护处理和舍入操作的2位填充位和另一个单精度乘法尾数的48位组成,保护位与舍入位的添加可以简化舍入运算。
由式(1)可知,在提取公共指数Ea+Eb+50-2p后,C*D结果尾数右移|Ec-(Ea+Eb+50)|位后,两个乘法结果尾数的小数点已对齐。设两个乘法指数阶差为d,则d=Ec+Ed-(Ea+Eb),根据式(1)提取出的公共指数Ea+Eb+50-2p,设对阶移位量为Shift_Bit,则Shift_Bit=Ec+Ed-(Ea+Eb+50)=d-50,不同的移位量会产生以下几种对阶移位情形:
a)Shift_Bit≥0时,尾数mC*mD相对其在98位对阶移位器中的最高位置左移或者不移动,则mA*mB的乘法结果只对粘贴位sticky位的计算有影响,sticky=|mA*mB,即A*B乘法结果的或值,左移时尾数后面填充的0对sticky位没有影响。
b)Shift_Bit<0且Shift_Bit≥-50时,尾数mC*mD要右移,移位量为|Shift_Bit|,但mC*mD最多右移50位,而mC*mD还处在98位移位器中,此时sticky位要等到尾数加法完成后才能计算出来。
c)Shift_Bit<-50且Shift_Bit≥-98时,说明移位量大于50,尾数mC*mD有一部分尾数会移出移位器,但不会完全移出,可以将sticky位分成两部分(sticky1和sticky2)计算:sticky1根据两个乘法结果尾数在加法完成后,将需要舍入的位进行或操作,sticky2是将移出移位器的尾数值进行或操作,最终的sticky=sticky1|sticky2。
d)Shift_Bit≤-98时,尾数mC*mD全部移出移位器,也可将sticky位分成两部分计算:sticky1是加法完成后需舍入的位数的或值,sticky2是移出移位器的尾数mC*mD的或值。
同理也设计了用于双精度浮点乘加运算的108位对阶移位器,该移位器也可以满足单精度浮点乘加运算的对阶移位。
规格化移位器是一个左移的移位器,为满足IEEE754浮点运算标准,在尾数进行加法后,结果尾数最高位有可能不为1,需根据计算出的前导零个数将结果尾数进行左移操作,使结果尾数最高位为1。双精度浮点乘加运算尾数为161位,最大只要一个161位的规格化移位器即可满足要求;单精度浮点乘加运算需要一个74位的规格化移位器;复数与点积运算需要一个98位规格化移位器。针对规格化移位的设计需求,设计了一个108位对数移位器。主要是对双精度的规格化移位作了优化,先判断计算出的结果尾数前导零个数是在前53位还是在后108位:若在前53位,则用移位器直接进行108位规格化移位要求;若在后108位,则结果尾数固定左移53位再用移位器进行108位移位.单精度浮点乘加与复数指令的规格化移位不需要再进行判断,使用108位规格化移位完全可以满足要求。
3FMAC模拟验证与综合优化
3.1FMAC验证
M-DSP中浮点MAC的验证主要从模拟验证和形式验证两方面来完成[12]。模拟验证主要借助Cadence公司的NC-Verilog等工具完成,包括模块级验证、系统级验证以及覆盖率分析等;形式化验证主要借助于ATEC(Advanced Test Equivalence Checking)和Formality等价性检查工具来完成。通过上述验证方法,发现了一些边界值错误和全局控制信号的控制错误,均已修正。
3.1.1黄金模型建立
模块级与系统级验证都需要验证大量功能点来保证功能的正确性,硬件仿真的结果需要与另一结果进行对比来判断,而另一结果的取得由于数据量大且有准确性高的要求,往往不能由人工计算得到,所以使用准确度高、速度快的软件方式计算结果对于提高验证工作效率十分必要。按照硬件逻辑的执行架构,使用C语言将每条指令的功能描述出来,并与硬件仿真调用同一组操作数,这一由软件建立的模型即为黄金模型。黄金模型的结果不依赖硬件,作为软件结果而独立存在,因此可以作为参考结果与硬件结果进行比较,方便检查硬件结果的正确性,同时节省大量资源。
3.1.2模块级验证
浮点MAC的验证首先从模块级验证开始,根据浮点数的数据结构和浮点MAC单元实现的指令,有针对性地加入相应的功能点测试激励,根据验证结果分析模块结构是否存在错误;模块级验证工具采用NC-Verilog仿真工具进行验证,通过编写特定的TestBench加入到模块级模拟验证环境中,查看激励响应,检测模块设计的正确性。对所有子模块完成充分验证之后,再在浮点MAC单元中进行功能验证,模块级验证主要内容如表2所示。
3.1.3系统级验证
系统级验证在单核情况下进行,通过汇编指令在高层次对FMAC进行验证,保证FMAC在系统级工作的正确性。系统级验证进行的主要验证工作有:
1)随机数测试。随机数验证主要是针对验证功能点与边界值时遗漏的测试点进行的验证,手工编写测试激励很难将边界值中的各种情况测试完全,根据浮点数据的结构特征,将生成的符号位、指数位、尾数位自由交叉组合生成伪随机数测试激励,在单核系统下测试1000万组随机数。
2)精度测试。进行精度测试主要是为了查看在相同的标准条件下,浮点运算的结果是否一致或误差的大小。在进行精度测试时,与Intel的Pentium Dual-core E5300 CPU和TI的TMS320C6678的运算结果进行了对比。由于TMS320C6678没有复数指令和乘加、乘减指令,所以测试结果与其有误差,但与Pentium E5300的结果完全一致。
3)流水线测试。指令流水线测试是为了验证处于系统级下的浮点MAC单元是否按预定的执行周期进行指令流水,浮点MAC单元共有9条指令,每条指令均能按照设计的流水节拍正确地执行写回。
4)全局信号测试。全局信号测试主要测试与外部模块通信的接口和信号的通信和控制,主要涉及到控制流水线的相关全局信号,包括全局暂停(Global Stall, G_Stall)信号、流水线冲刷(Pipeline_Flush, P_Flush)信号、派发暂停(Instruction Dispatch Snop, ID_Snop)信号以及条件执行(Condition Execution, Cond_Exe)信号。以全局信号测试为例,当全局信号G_Stall为高时,指令暂缓执行,等到为低时流水线继续执行,其测试波形如图6所示。
5)指令组合测试。M-DSP中MAC单元包括3个执行单元:浮点MAC单元、定点MAC单元和浮点ALU单元,三条执行通路共用一套读写端口,因此,在对浮点MAC指令进行验证时,与其他单元的指令组合验证是必要的,不仅可以检查本单元的正确性,还可以验证整个MAC流水线通路的正确性。
3.1.4形式验证
形式验证(Formal Verification, FV)是一种集成电路(Integrated Circuit, IC)设计的验证方法,它从静态的角度对设计进行验证,不需要模拟验证的激励。ATEC等价性检查工具采用形式化的验证方法,将RTL代码与C语言编写的黄金模型转化为可以比较的表达式,在相同的约束条件下进行等价性验证,保证硬件设计的正确性。验证初期已对浮点MAC单元的每条指令建立C语言黄金模型,ATEC等价性检查的流程如图7所示。由于FMAC模块的复杂性,在进行ATEC验证过程中,当存在错误时,会快速地举出反例测试激励,可以通过给出的测试激励进行错误定位,大幅缩短设计周期。Formality等价性检查旨在验证综合前的RTL代码与综合后的门级网表是否等价。
3.2逻辑综合
浮点MAC单元采用Synopsys公司的DC工具进行逻辑综合,综合环境是基于40nm工艺库,在Typical条件下进行综合,综合的目标频率是1GHz,留给后端物理设计的时间大约是30%,剩下的前端的时钟周期大约为450ps,寄存器的输入延时设置为100ps,输出延时设置为100ps。
采用上述综合约束条件,对浮点MAC单元的乘法器模块和MAC运算主体结构流水线进行逻辑综合,浮点MAC单元综合结果如表3所示,单个浮点MAC单元综合面积35250μm2,总功耗6.7570mW,其中动态功耗6.0432mW,静态功耗713.7950μW,最长关键路径450ps。与参考文献[8]中的FMAC结构相比,本文采用单双精度通路分离的乘加结构,虽然通路分离,但精简了逻辑设计,降低了硬件设计的复杂度,有效减少了硬件开销;文献[8]中的浮点MAC采用单一的浮点乘加结构,虽然复用了大部分逻辑资源,但增加了逻辑设计的复杂度,很多硬件资源并没有有效复用,从而导致面积较大,本文所设计的FMAC在硬件资源开销上比参考结构在性能提高了2.17%,单元面积减少了12.95%。
4结语
本文详细设计了M-DSP中浮点MAC单元,根据浮点MAC单元的指令功能和性能要求,设计和实现了单、双精度通路分离的6级流水线浮点MAC单元,针对每个功能单元进行了详细设计,并对乘法器等关键模块进行了优化设计。全面验证了所设计的浮点MAC单元,基于40nm工艺对浮点MAC单元采用DC综合工具进行综合,综合结果表明所设计的浮点MAC单元工作频率可达1GHz,功耗6.7570mW,面积35250μm2。整个M-DSP芯片1GHz下峰值处理性能达到单精度浮点复数乘法25GFLOPs(Giga FLoating-point Operations Per second)、单精度浮点100GFLOPs、双精度浮点50GFLOPs,满足M-DSP芯片对浮点乘加运算的高性能要求。
参考文献:
[1]李海森,李思纯,周天.高速DSP原理、应用与试验教程[M].北京:清华大学出版社,2009:23-47. (LI H S, LI S C, ZHOU T. High Speed DSP Principle, Application and Experiment Course [M]. Beijing: Tsinghua University Press, 2009: 23-47.)
[2]方维,孙广中,吴超,等.一种三维快速傅里叶变换并行算法[J].计算机研究与发展,2011,48(3):440-446. (FANG W, SUN G Z, WU C, et al. A parallel algorithm of three-dimensional fast Fourier transform [J]. Journal of Computer Research and Development, 2011, 48(3): 440-446.)
[3]WANG X, ZHANG Y, WANG F, et al. A configurable floating-point discrete Hilbert transform processor for accelerating the calculation of filter in Katsevich formula [J]. WSEAS Transactions on Communications, 2012, 11(11): 395-404.
[4]张拥军,陈艇.基于软件无线电的并行多输入多输出均衡技术[J].计算机应用,2015,35(4):1179-1184. (ZHANG Y J, CHEN T. Parallel multiple input and multiple output equalization based on software defined radio [J]. Journal of Computer Applications, 2015, 35(4): 1179-1184.)
[5]MONTOYE R K, HOKENEK E, RUNYON S L. Design of the IBM RISC System/6000 floating-point execution unit [J]. IBM Journal of Research and Development, 1990, 34(1): 59-70.
[6]LANG T, BRUGUERA J D. Floating-point fused multiply-add with reduced latency [J]. IEEE Transactions on Computers, 2004, 53(8): 988-1003.
http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=1306992&url=http%3A%2F%2Fieeexplore.ieee.org%2Fiel5%2F12%2F29016%2F01306992
http://xueshu.baidu.com/s?wd=paperuri%3A%280abb7fbed27abc68d04bc9efe4c31c30%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdl.acm.org%2Fcitation.cfm%3Fid%3D846996&ie=utf-8&sc_us=16446173281281047444
ICCD '02 Proceedings of the 2002 IEEE International Conference on Computer Design: VLSI in Computers and Processors (ICCD'02)
Page 145
IEEE Computer Society Washington, DC, USA ?2002
[7]LANG T, BRUGUERA J D. Floating-point fused multiply-add: reduced latency for floating-point addition [C]// ARITH 05: Proceedings of the 17th IEEE Symposium on Computer Arithmetic. Washington, DC: IEEE Computer Society, 2005: 42-51.
[8]田甜.FT-XDSP中FMAC单元的研究与实现[D].长沙.国防科学技术大学,2013:56-57. (TIAN T. The research and implementation of high performance SIMD floating-point multiplication accumulator unit for FT-XDSP [D].Changsha: National University of Defence Technology, 2013: 56-57.)
[9]彭元喜,杨洪杰,谢刚.X-DSP浮点乘法器的设计与实现[J].计算机应用,2010,30(11):3121-3126. (PENG Y X, YANG H J, XIE G. Design and implementation of float point multiplier in X-DSP [J]. Journal of Computer Applications, 2010, 30(11): 3121-3126.)
[10]何军,黄永勤,朱英.分离通路浮点乘加器设计与实现[J].计算机科学,2013,40(8):28-33. (HE J, HUANG Y Q, ZHU Y. Design and implementation of separated path floating-point fused multiply-add unit [J]. Computer Science, 2013, 40(8): 28-33.)
[11]RUBINFIELD L P. A proof of the modified Booths algorithm for multiplication [J]. IEEE Transactions on Computer, 1975, 24(10): 1014-1015.
[12]陈海燕,郭阳,刘祥远,等.集成电路计算机辅助设计与验证实践[M].长沙:国防科技大学出版社,2010:210-220. (CHEN H Y, GUO Y, LIU X Y, et al. The Practice of Computer Aided Design and Verification of Integrated Circuits [M]. Changsha: National University of Defence Technology Press, 2010: 210-220.)

