Flow, thermal criticality and transition of a reactive third-grade fluid in a pipe with Reynoldsʼ model viscosity*
Samuel S. OKOYA
Flow, thermal criticality and transition of a reactive third-grade fluid in a pipe with Reynoldsʼ model viscosity*
Samuel S. OKOYA
Department of Mathematics, Obafemi Awolowo University, Ile-Ife, Nigeria, E-mail: sokoya@oauife.edu.ng (Received September 5, 2014, Revised January 22, 2015)
Neglecting the consumption of the material, a steady incompressible flow of an exothermic reacting third-grade fluid with viscous heating in a circular cylindrical pipe is numerically studied for both cases of constant viscosity and Reynolds’ viscosity model. The coupled ordinary differential equations governing the flow in cylindrical coordinates, are transformed into dimensionless forms using appropriate transformations, and then solved numerically. Solutions using Maple are presented in tabular form and given in terms of dimensionless central fluid velocity and temperature, skin friction and heat transfer rate for three parametric values in the Reynoldsʼ case. The numerical results for the velocity and temperature fields are also presented through graphs. Bifurcations are discussed using shooting method. Comparisons are also made between the present results and those of previous work, and thus verify the validity of the provided numerical solutions. Important properties of thermal criticality are provided for variable viscosity para- meter and reaction order. Further numerical results are presented in the form of tables and graphs for transition of physical parame- ters, while varying certain flow and fluid material parameters. Also, the flow behaviour of the reactive fluid of third-grade is com- pared with those of the Newtonian reactive fluid.
non-Newtonian fluids, third-grade fluid, thermal transition, heat generation, temperature dependent viscosity, numerical solutions
Introduction
The phenomenon of Newtonian flow and heat transfer in a cylinder on physically reasonable assu- mptions has been analyzed by a number of authors[1]and the references therein. It is now generally known in industrial applications that the non-Newtonian flui- ds, particularly the fluid of third-grade, are more suita- ble than Newtonian fluids. Some of the applications in processing industries include food processing, poly- mer processing and petrochemical applications. For problems involving heat transfer processes in fluids of third-grade, a complete thermodynamics analysis of the constitutive function has been performed (see rela- ted work by some authors[2,3]etc.). In this specialthe case of third grade fluids, the governing equations re- duces to that which one would get for an appropriate generalized Newtonian fluid.
These studies have little or no emphasis on the effects of variable viscosity and heat transfer on the flow. Some other studies involving variable viscosity models have no consideration of heat generation in the system, see for example Massoudi and Christe[4]. Reference [4] solved and analyzed numerically, the effects of temperature dependent viscosity for Reynoldsʼ and Vogelʼs model cases for a pipe. Appro- ximate analytical solutions for Reynolds’ and Vogelʼs model cases for a pipe were revisited using perturba- tion technique, while the criteria for which the solu- tions are valid were determined by Yürüsoy and Pakdemirli[5]. The problem of Reynoldsʼ and Vogelʼs temperature dependent viscosity models for third grade fluids in a cylindrical pipe is studied using ho- motopy analysis method by Ellahi et al.[6].
Most of these studies mentioned above, are based on non-reactive flow properties. More accurate predi- ction for the flow and heat transfer can be achieved by including exothermic reaction under Arrhenius kineti- cs, but we have neglected reactant consumption of the materials. Some of the earlier investigations on criti- cality and disappearance of criticality of a reactive viscous fluid with or without flow are: A new numeri- cal method was employed to calculate criticality and transition (disappearance of criticality) for a range of Biot number for Arrhenius and Bimolecular tempera- ture dependence in the cases of infinite slab, infinite cylinder and sphere in the absence of flow, see Boddington et al.[7]. Also, Zaturska[8]considered plane Couette flow, Poiseuille pipe flow, axial and rotating flows between concentric circular cylinders using power series and assuming the Frank-Kamenetskii ex- ponential approximation to the Arrhenius term. Fur- thermore, Shonhiwa and Zaturska[9]adopted the shoo- ting method and solved numerically for the disappea- rance of criticality, for the reactive viscous flows stu- died in Ref.[8]. Quite recently, Britz et al.[10]provided numerical solutions to the equation for thermal expan- sion of a reacting gas, exploring both steady state and time-marching solutions for the infinite slab, cylinder and sphere. It is worthy of attention that the critical conditions of the form described above are significant in providing safety criteria both for storage and for handling.
A number of studies in the literature do not ex- plain the effects of variable viscosity, heat transfer and generation of reaction heat inside the pipe on the non- Newtonian fluid. In fact, very little work has been re- ported, which deals with flow of a reacting non-linear fluid. Bridges and Rajagopal[11], by direct integration, investigated the pulsatile pipe flow of a chemically- reacting fluid whose viscosity depends on the concen- tration of a species (constituent) that is governed by a convective-reaction diffusion and the velocity gradient. Approximate solutions are constructed for the pro- blem with heat source term, using regular perturbation techniques together with a special type of Hermite- Pade approximants, while important properties of the velocity and temperature fields including thermal cri- ticality conditions are discussed in Makinde[12]for iso- thermal wall. Other numerical studies involving the competing effects of conduction, dissipation, heat ge- neration and radiation for the flow of non-linear fluids are contained in Massoudi and Phuoc[13]and the refe- rences contained therein. Ajadi[14]studied the criticali- ty of a one-step exothermic, reactive third-grade liquid flowing steadily through a cylindrical pipe with iso- thermal wall for a variable spatial dependent viscosity via homotopy analysis method and variational techni- que on the momentum and energy equations, respecti- vely. Recently, Chinyoka and Makinde[15]derived the coupled nonlinear equations in cylindrical coordinates governing pressure-driven unsteady flow of a reactive fluid of viscosity with an exponentially decreasing function of temperature, and solved numerically, using semi-implicit finite difference schemes, under axisymmetric conditions. Also, Chinyoka and Makinde[16]solved numerically, using an unconditio- nally stable and convergent semi-implicit finite diffe- rence scheme, the transient flow of a reactive variable viscosity third-grade fluid in a cylindrical pipe with convective heat exchange at the pipe surface. More re- cently, Ireka and Chinyoka[17]studied numerically, using semi-implicit finite difference techniques, the effect of wall slip on the flow and heat transfer for the reactive Johnson-Segalman fluid in a lubricated pipe with exponential viscosity.
The works carried out by Ajadi[14], Bridges and Rajagopal[11], Makinde[12], Massoudi and Phuoc[13]are obviously a major step towards understanding the role of non-linear fluids with (or without) variable viscosi- ty under heat generation with Arrhenius kinetics, while restricting their analysis up to thermal explosion (critical value). It should be conceded that a realistic mathematical description of thermal explosion needs to include the effects of Arrhenius temperature depe- ndence with variable pre-exponential factor (see, for example Adegbie[18]and Okoya[19]) and Reynoldsʼ vis- cosity model (see Massoudi and Christe[4], Ireka and Chinyoka[17]and Jayeoba and Okoya[20]).
In this study, reactive generalized Newtonian fluid flow in pipe is considered while fluid friction and Nusselt number are formulated. The coupled di- mensionless governing equations of momentum and energy are solved numerically by using Maple routine codes. A third-grade fluid model is accommodated, while Reynoldsʼ model accounted for the temperature- dependent viscosity in the analysis. The central velo- city and temperature, fluid friction and Nusselt num- ber are presented in tabular form, while the velocity and temperature profiles are presented graphically. Thermal critical values are computed for various va- lues of viscosity parameter and reaction order while competing effects of non-Newtonian parameter, pre- ssure gradient parameter, viscous dissipation parame- ter and index of the pre-exponential factor on constant viscosity and Reynolds’ model viscosity (cases) are treated separately. The solutions for reactive Navier- Stokes fluid can be deduced as a limiting case of our solutions.
1. Governing equations
Consider the fully developed laminar motion th- rough a circular Poiseuille device. We employ cyli- ndrical coordinates, with theaxis coinci- ding with the axis of the pipe. Hereis the distance measured radially, such thatis the radius of the pipe andis the azimuthal angle (see Fig.1).
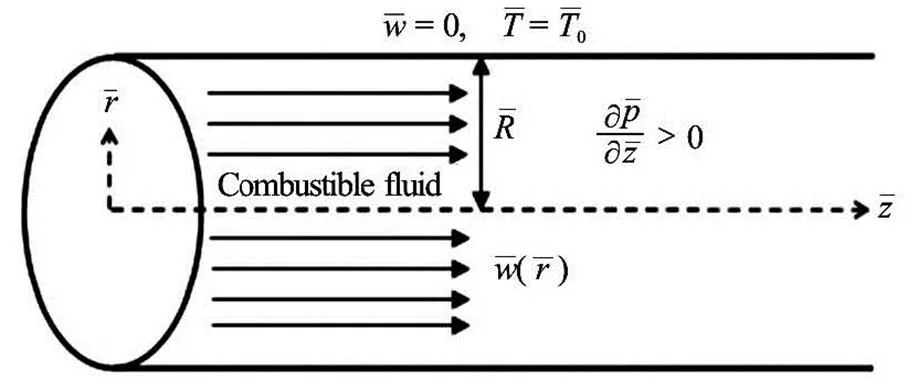
Fig.1 Flow configuration and coordinate system of the problem
Assuming incompressible flow, in the absence of chemical reactions and electromagnetic effects, the equations of motion are the continuity, linear momen- tum and energy equations,
and
For the heat flux vector we adopt the classical Fourierʼs law of heat conduction, so that
It is a well known fact that majority of the pre- vious studies have dealt with systems having constant viscosity as a good approximation (i.e.). On the other hand, important issues related to systems po- ssessing temperature dependent viscosities are scienti- fically appealing and challenging, with a wide range of industrial applications. Our review of literature has been based on fluid viscosity, which usually has a st- rong dependence on temperature. There have been se- veral studies involving, in particular, Reynolds’ model viscosity, for example in the case where the functiontakes the form,
The constitutive equation for a third-grade fluid is
For the problem under consideration, we seek ve- locity and temperature fields of the form:
while Eq.(3) reduces to
The problem is simplified by writing the equatio- ns in the non-dimensional form. We define the follo- wing non-dimensional quantities,
In terms of the above non-dimensional variables and parameters, Eqs.(13)-(15) take the form
where
is the dimensionless viscosity. These dimensionless equations cannot be integrated analytically, and it is very important to develop efficient numerical method to solve them. Evidently, the special case ofco- rresponds to constant viscosity case.
2. Particular cases
(1) In the absence of non-Newtonian field, rea- ction order and constant viscosity i.e.,and, respectively, the results for critical values withand disappearance of criticality of the pre- sent paper are reduced to Zaturska[8]and Shonhiwa and Zaturska[9], respectively.
(2) In the absence of reaction order and constant viscosity i.e.and, respectively, the re- sults of the present paper are reduced to the critical values obtained by Makinde[12].
(3) In the absence of heat source i.e, the resu- lts of the present paper are reduced to those studied by numerous authors such as Massoudi and Christe[4]and Yürüsoy and Pakdemirli[5].
3. Numerical solution
To start the integration of the differential Eqs.(16), (17) by Maple standard solver, poses a pro- blem since it contains a singularity in the neighbour- hood of the axis of the pipe (i.e.). This pro- blem is handled numerically by developing equations that do not contain a singularity. Applying LʼHospital rule[4](or Maclaurin expansion[9,10]) we have
so that the differential Eqs.(16) and (17) reduce to
The new differential Eqs.(21), (22) are valid near0. It is evident that the boundary conditions atare specified in a straightforward manner. Such me- thods have been used successfully for thermal explo- sion problems (see for example, Shonhiwa and Zaturska[9]and Britz et al.[10]), and non-reactive third- grade fluid (see e.g., Massoudi and Christe[4]).
Firstly, the systems of non-linear differential equations together with the boundary conditions (i.e. Eqs.(16)-(19), (21), (22)) were solved numerically fo- llowing procedure based on the Maple. Maple uses the Runge-Kutta-Fehlberg fourth fifth order (RFK45) me- thod as one of its standard numerical solvers to gene- rate the numerical solution of a boundary value pro- blem. Practical tests indicate that the neighborhood of the axis of the pipe (to start the integration) for the constant viscosity case, has been taken small enough and kept invariant throughout the run of the program, while slightly higher for the Reynolds’ model. In all the calculations, the finite length of the device is igno- red and the computations performed for infinitely long cylinders. For comparison of the results, numerical va- lues are recorded in Table 1 forand. Hereandare the values of the maximum velo- city and temperature at the pipe axis. It is observed from Table 1 that the numerical values ofandin the present paper whenand, are in good agreement with the results obtained by Massoudi and Christe[4]. These authors have used fini- te difference technique as compared to our Maple sol- ver.
Table 1 Values and are compared with Massoudi and Christe[4]
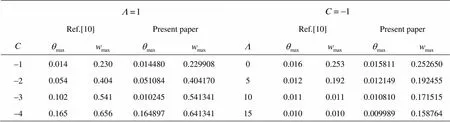
Table 1 Values and are compared with Massoudi and Christe[4]
Ref.[10]Present paperRef.[10]Present paper -10.0140.2300.0144800.22990800.0160.2530.0158110.252650 -20.0540.4040.0510840.40417050.0120.1920.0121490.192455 -30.1020.5410.0102450.541341100.0110.0110.0108100.171515 -40.1650.6560.1648970.641341150.0100.0100.0099890.158764
Two other quantities of interest are the skin-fri- ction at the wall and Heat transfer rate which is esti- mated in terms of Nusselt number. The skin-fri- ction, related to the shear stress at the wall, is related toand the Nusselt number is rela- ted to. There are basically three in- dependent non-dimensional parameters,,andwhich were not considered in Massoudi and Christe[4], but in our present work we will only study the influe- nces of this triplet. The table of values of,,andare presented in Table 2. In addition, Figs.2-5 present the results showing few representati- ve figures of the velocity distributions and temperatu- re profiles across the pipe, for different values of the governing parameters.
Table 2 Effects of , and in Reynolds’ model when
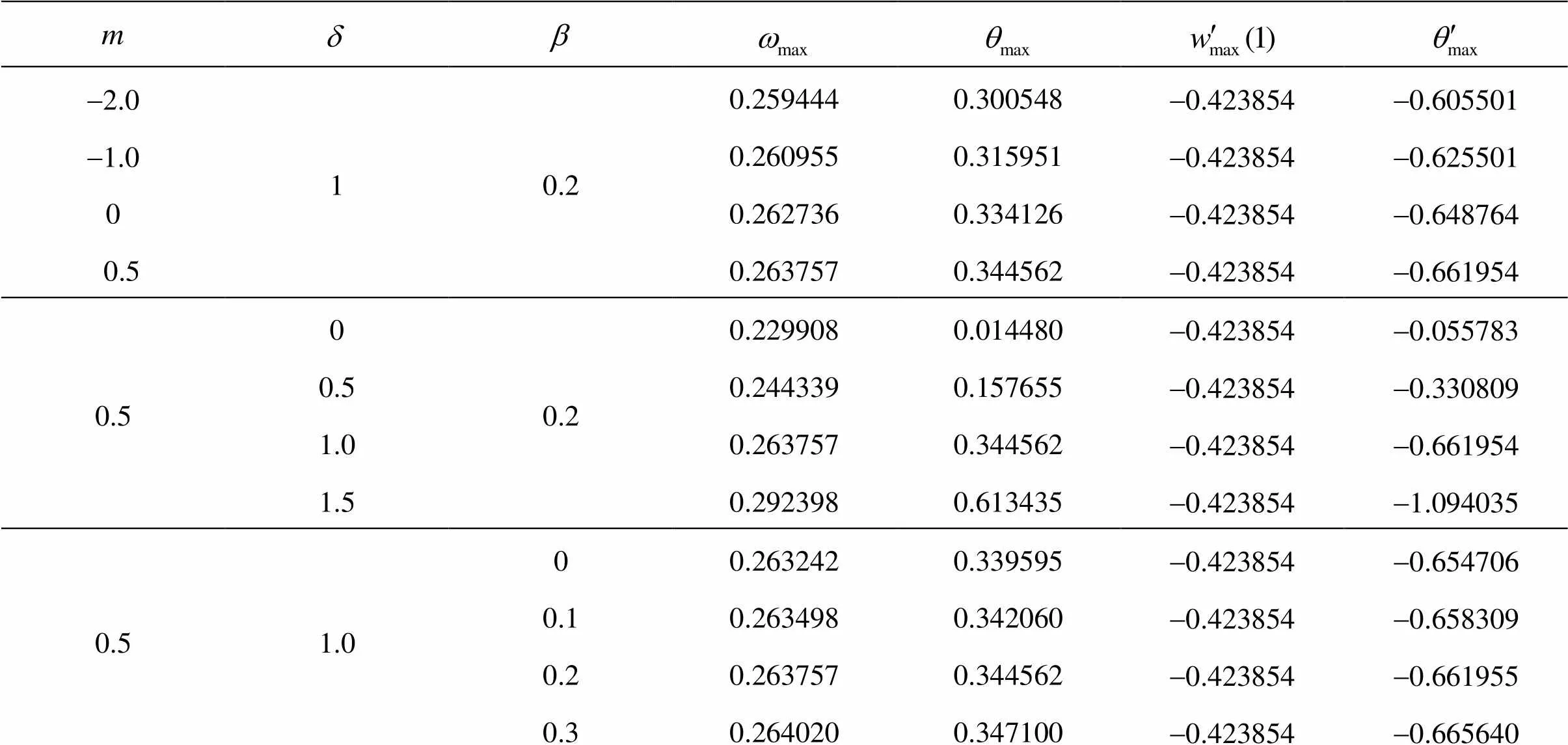
Table 2 Effects of , and in Reynolds’ model when
-2.010.20.2594440.300548-0.423854-0.605501 -1.00.2609550.315951-0.423854-0.625501 00.2627360.334126-0.423854-0.648764 0.50.2637570.344562-0.423854-0.661954 0.500.20.2299080.014480-0.423854-0.055783 0.50.2443390.157655-0.423854-0.330809 1.00.2637570.344562-0.423854-0.661954 1.50.2923980.613435-0.423854-1.094035 0.51.000.2632420.339595-0.423854-0.654706 0.10.2634980.342060-0.423854-0.658309 0.20.2637570.344562-0.423854-0.661955 0.30.2640200.347100-0.423854-0.665640

Fig.2 Velocity field for various non-Newtonian parameter when , , and
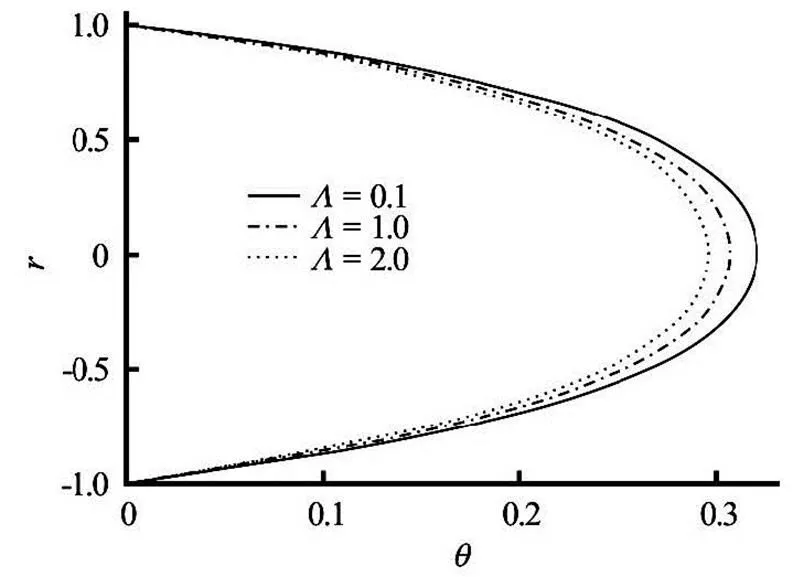
Fig.3 Temperature profile for various non-Newtonian parame- ter when when , , and
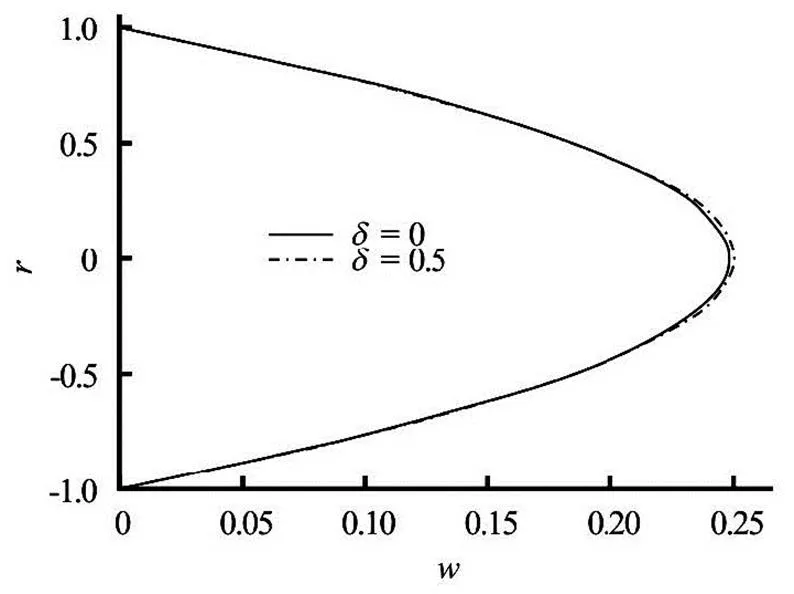
Fig.4 Velocity field for various Frank-Kamenetskii parameter when , , and
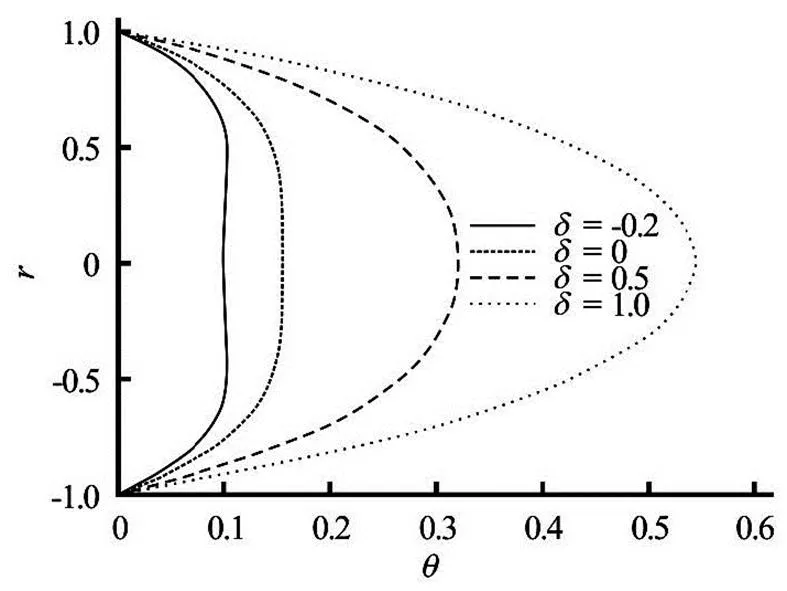
Fig.5 Temperature distribution for various Frank-Kamenetskii parameter when , , 0.1 and
It is worth noting that the steady state velocity and temperature distributions in Figs.2-5 may only de- pend on certain physical parameter range. Conseque- ntly, the reaction term, will need to be carefully controlled as “large” values can lead to disappearance of steady solution, as illustrated in Fig.6.
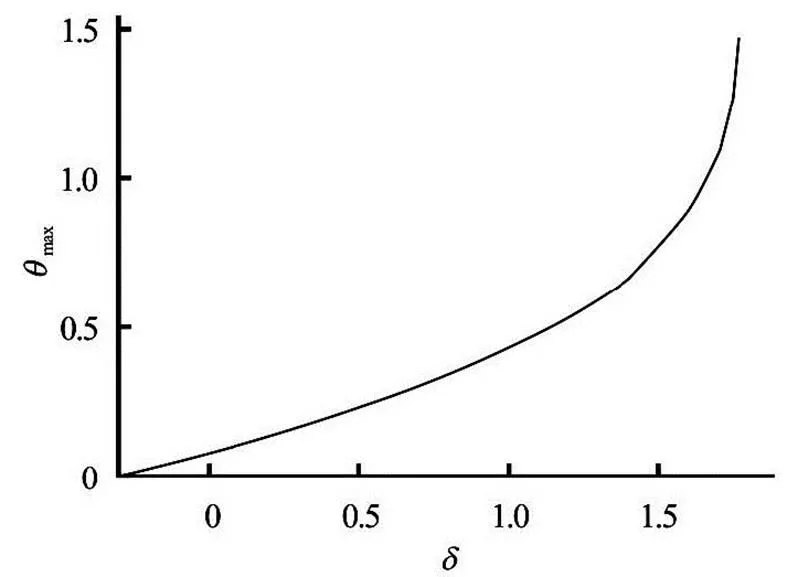
Fig.6 Disappearance of fluid steady state temperature at large
We next solve the systems of non-linear differe- ntial equations together with the boundary conditions (i.e. Eqs.(16)-(19), (21), (22)) by the method based on the Maple shooting method strategy, modified to some extent to cope with singularity and non-linearity, with the unknown parameter taken to be. Forthere are solutions only for, the critical modified Frank-Kamenetskii parameter, and in this range there exist two solutions for the steady state. Criticality sig- nifies the onset of the nonexistence of a steady state solution. Whenforthere are three so- lutions of the problem corresponding to a maximum and a minimum (i.e. explosion and extinction, respe- ctively). As a result of the disappearance of criticality (i.e. transition), the three solutions merge into one. The mathematical expression for criticality corre- sponds to, while the disappearance of criticality corresponds to.
To see if the program runs correctly for critical values, and to make quantitative comparisons between this and other established methods, we consider the following simplified problems. The important findings are highlighted in Tables 3, 4 below.
Table 3 Values of for different values of and are compared with results obtained by Makinde[12] when , , Ref.[12]OursRef.[12]Ours DifferenceDifference 01.9454361.9461947.58´10-42.2068382.2076818.43´10-4 0.11.9460711.9467787.07´10-42.2074762.2082687.92´10-4 0.21.9467551.9473225.67´10-42.2081612.2088126.51´10-4 0.31.9474821.9478283.46´10-42.2088892.2093194.29´10-4
Table 4 Comparison of different numerical solutions for transition when

Table 3 Values of for different values of and are compared with results obtained by Makinde[12] when , ,
Model 1Model 2Model 3 and and Ref.[7]OursRef.[9]OursRef.[7]Ours 0.2421070.2421090.242110.242110.3315610.331566 3.0091223.0076903.006303.008882.6999152.699664 5.9433545.9367565.943255.932366.2593286.247736 1.4390001.4370001.439001.436002.0750002.072000
For illustration of the results of criticality and disappearance of criticality, numerical values are plo- tted in Fig.7 for Reynoldsʼ case and various.
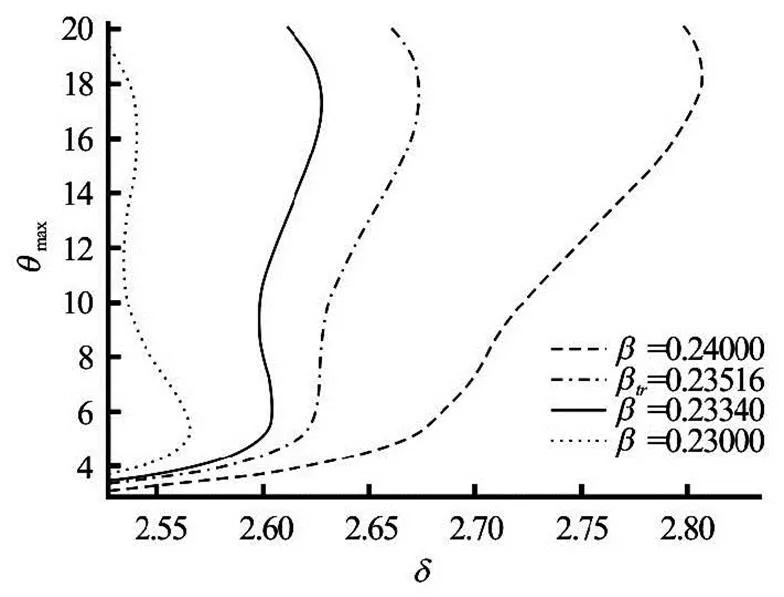
Fig.7 Understanding thermal transition with variable viscosity when , , and
It is worthy of mention that the velocity Eq.(16) and the energy Eq.(17) are different from Eqs.(1), (2) in Makinde[12]due to the terms associated with varia- ble viscosity parameter and the reaction order. Since the effects of,andon the distribu- tion of dimensionless velocity and energy have been discussed in Makinde[12], in our present work, we will only investigate the effect ofandon the flow equations. To perform this, we keep,,and. Figures 8, 9 show the effect of variable viscosity parameter and reaction order on the dimensionless velocity and temperature profiles obtai- ned using the standard Maple routine.
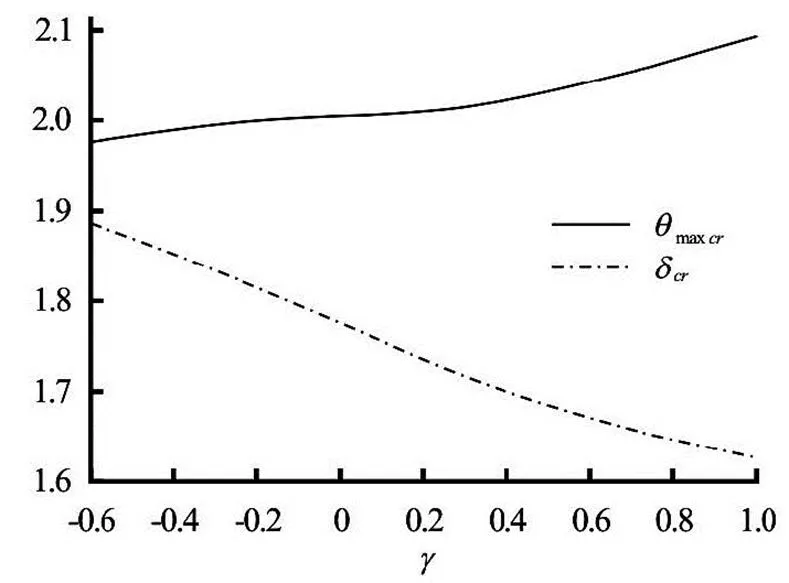
Fig.8 Plots of thermal critical values against γ when

Fig.9 Profiles of thermal critical values versus m when 0.2
Furthermore, computation through employed nu- merical code has been carried out for various non-di- mensional values of non-Newtonian parameter,viscosity index, pressure gradient variation, index of the pre-exponential factorand viscous dissipation, so as to investigate the effects on the disappearance of criticality (transition). The study en- compasses within its realm both reactive third grade and first grade (Newtonian) fluids, while results are displayed graphically, and in some cases, depicted in tabular form. Also, results are presented for constant viscosity and Reynolds’ viscosity model in Figs.10-15 and Tables 5, 6.
Table 5 Illustrating transition for , and Constant viscosityReynolds’ model -2.00.130463.810756.205680.130473.806866.19972 00.241863.002325.949600.241902.999345.94172 0.50.331102.692766.275760.331172.691196.25736
Table 6 Some transitional values when , , and
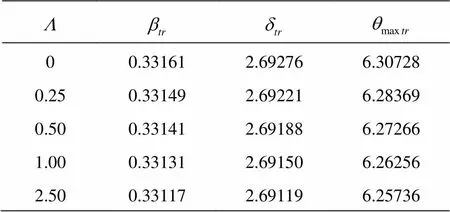
Table 5 Illustrating transition for , and
00.331612.692766.30728 0.250.331492.692216.28369 0.500.331412.691886.27266 1.000.331312.691506.26256 2.500.331172.691196.25736
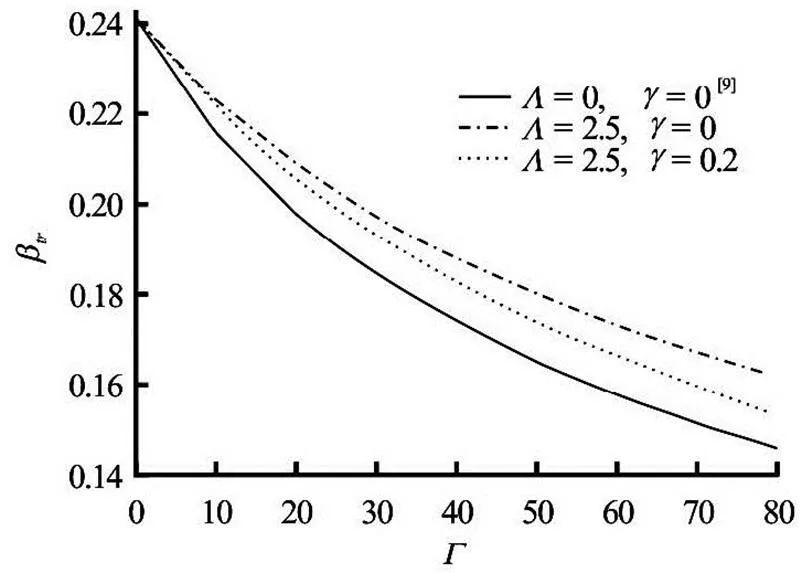
Fig.10 as a function of viscous heating parameter when and : effects of and
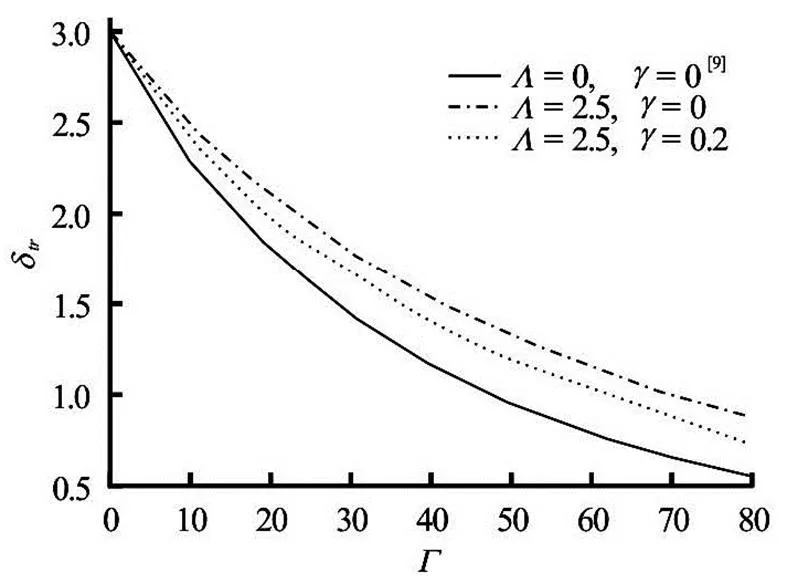
Fig.11 versus viscous heating parameter when ‒2 and : effects of and

Fig.12 versus viscous heating parameter when ‒2 and : effects of and
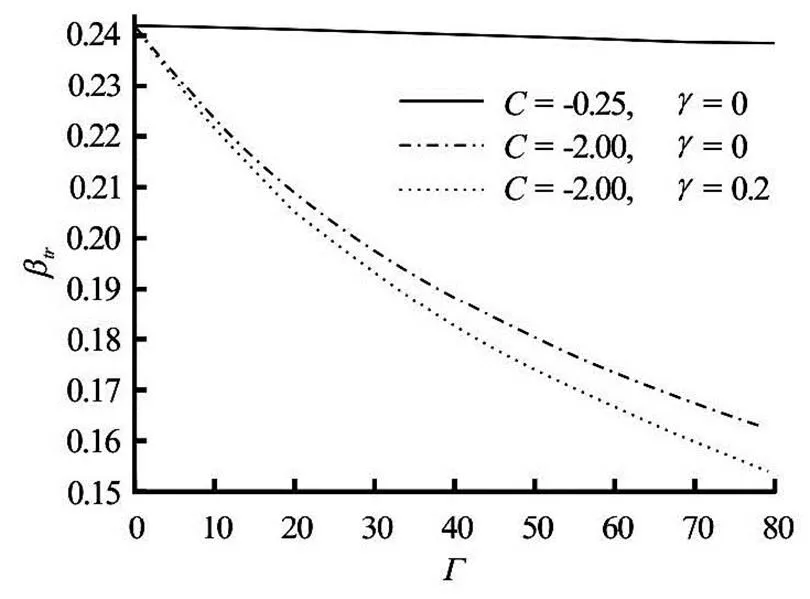
Fig.13 as a function of viscous heating parameter when and : effects of and

Fig.14 as a function of viscous heating parameter when and : effects of and
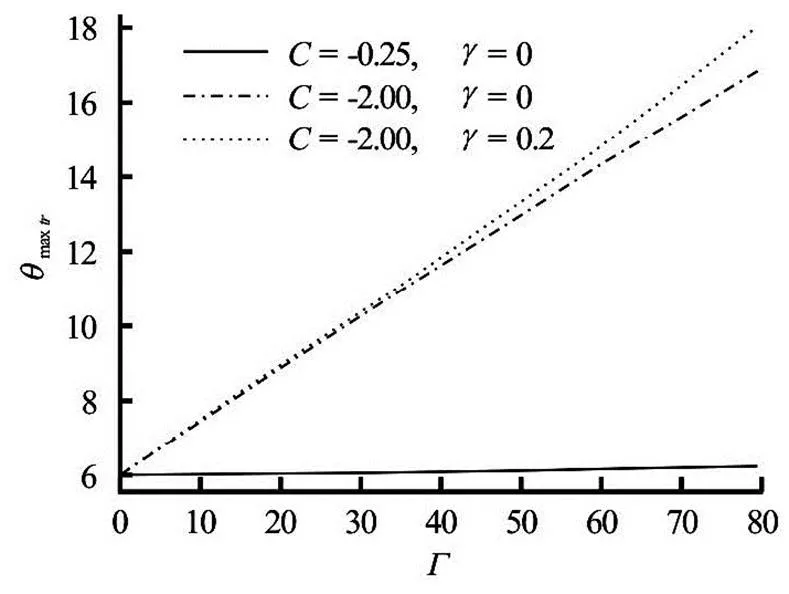
Fig.15 versus viscous heating parameter when 2.5 and : effects of and
4. Analysis of results
Table 2 shows the influences of,andon the velocity and temperature at the axis of the cy- linder, as well as velocity and temperature gradients at the wall. We observed that as each of the triplet in- creases, the velocity gradient remains constant. It can be seen that whenandincrease there is no sig- nificant incremental change in the values ofandabsolute values of the temperature gradient, whereas whenincreases, there are tremendous in- creases in the values of,and absolute va- lues of the temperature gradient. The latter happens generally in heating systems. When the studies with heat flow problem in absence of activation energy pa- rameter,, are compared, one finds that the heat flow is slightly stronger in the present case.
The influence of non-Newtonian parameteron the flow distribution is displayed in Figs.2, 3. It is evident from Figs.2, 3 that the fluid velocity and tem- perature generally decrease due to increase in. In- variably the solution for the Newtonian casecorresponds to the upper solution. Also, the effect of Frank-Kamenetskii parameter, due to the genera- lized Arrhenius kinetics on the fluid velocity and tem- perature, is displayed in Figs.4, 5. It is shown that fluid velocity and temperature increase due to increase in. The effect ofis more pronounced for the temperature field than the velocity distribution, as ex- pected on physical grounds. It is worth noting that non-Newtonian parameterhas opposed behaviour, as compared to the Frank-Kamenetskii parameter.
In Fig.10 (or Fig.11), we have plotted(or) profiles, showing the effects of non-Newtonian para- meter, viscous heatingand the viscosity para- meter(in the case of Arrhenius reaction model when the pressure is kept constant) on the flow setup. In the former, it can be seen thatdecreases when the viscous heating parameter(or viscosity para- meter) increases, but increases with increase in the non-Newtonian parameter. Similar behavior was observed forin the latter. It is evident that for,andare lower limits ofand.
In addition, comparing the results of transitional values of Shonhiwa and Zaturska[9]for reactive Newtonian fluid, the triplet reaction parameters (in Figs.10-12) have exactly the same pattern, thoughandin the case of reactive non-Newtonian fluid are higher except for.
It is expedient to note from Figs.2, 3 (or Figs.10- 12) that the influence ofon velocity and tempera- ture (or,and) is similar to that of Newtonian model qualitatively, but differs quantitati- vely with Refs.[10] (or [16]).
The influence of pressure gradient variation, the viscous heating parameterand the viscosity pa- rameter, on the triplet (,and) is shown in Figs.13-15 for Arrhenius reaction model in the non-Newtonian case. For given values of, it is clearly seen thatand(or) increase (or decreases) with an increase in pressure gradient para- meter, while for a given, the variation ofandhave opposite effects on the triplet parameters.
Table 5 (see in particular the first four blocks) shows the variation of,andwith index of the pre-exponential factorfor. For a significant practical case, we focus our attention on. It is evident that(or) is in- creasing (decreasing) with, whileis a con- cave function of. Also, we observed that the para- metersand(orare monotonically de- creasing (or slightly increasing) with the viscosity pa- rameter. In addition, for given values of(in the non-Newtonian reactive flow),(or) for the case of Sensitized reaction is smallest (or biggest) when compared with the Arrhenius and Bimolecular, while, for the Arrhenius case is smallest when compared with the others.
In order to illustrate the effects on the triplet pa- rameters for Bimolecular model reaction, see Table 6. It can be noted from the table that an augment inyields a diminution in the triplet (,and).
5. Conclusions
This parametric study investigates the heat tran- sfer characteristics for pipe flow of a reactive third- grade fluid with Reynoldsʼ model viscosity with appli- cations in processing industries. The independent di- mensionless numbers which are varied are,,,and. The following concluding remarks emerge from this study.
(2) Fluid velocity and temperature decrease due to increase in, while the reverse effect is observed with respect to.
(3) In general, there are two critical values (ex- plosion and extinction) and with the disappearance of criticality (transition), the critical values merge, corre- sponding to a point of inflexion, and thereafter the graph grows continuously. But in our model, we see a minor exception to this general rule in the Reynoldsʼ viscosity model with respect to the viscous dissipation parameter,. In theplane, we found that the curve has a third critical value atandwhen. However, at tran- sitionand larger values of, the new critical value persists.
(4) It is found that the investigated third-grade non-Newtonian fluid transition shows a larger appare- nt viscosity than the corresponding Newtonian fluid transition. In fact, as the non-Newtonian property in- creases (or deceases), the transitional values ofandincrease (ordecreases), for both constant and variable viscosity models.
(5) It should be pointed out that as the pressure gradienttends to zero for the Newtonian case, the triplet, as a function of, tends to be parallel to the axis. However, this is not the case for the non- Newtonian scenario. These results and observations may have interesting implications for the experime- ntalist studying (non)-Newtonian reactive flows.
(6) It is clearly evident that non-Newtonian mate- rial parameter appears to be a relevant phenomenon and cannot be ignored.
(7) The results on the triplet parameters, as a fun- ction of, for the Bimolecular reactionis also fascinating. Asincreases from 0 to 0.3, the triplet decreases gradually, whereas the reverse is the case in the Arrhenius reaction foronly.
(8) The influence of the viscosity parameteron the transitional values of the triplet is more pronou- nced asbecomes larger, and the opposite is true for increasing the exponent.
Acknowledgments
This work was supported by Pastor E. A. Adeboye endowed Professorial Chair and conducted at the Department of Mathematics, University of Lagos, Lagos, Nigeria while on leave from Obafemi Awolowo University, Ile-Ife, Nigeria. Also, the author appreciates the helpful comments of two reviewers which led to the improvement of the paper.
References
[1] ERDOGAN M. E., IMRAK C. E. On the flow in a uni- formly porous pipe[J]. International Journal of Non- Linear Mechanics, 2008, 43(4): 292-301.
[2] MOTSA S. S., MAKINDE O. D. and SHATEYI S. On the successive linearisation approach to the flow of reactive third-grade liquid in a channel with isothermal walls[J]. Mathematical Problems in Engineering, 2013, Article ID 635392.
[3] ANANTHASWAMY V., CHOWMIYA C. and SUBHA M. Approximate analytical solution of thermal criticality for a reactive third-grade liquid in a channel with isothe- rmal walls: homotopy analysis method[J]. Discovery, 2014, 21(67): 53-70.
[4] MASSOUDI M., CHRISTE I. Effects of variable viscosity and viscous dissipation on the flow of third grade fluid in a pipe[J]. International Journal of Non-Linear Mecha- nics, 1995, 30(5): 687-699.
[5] YÜRÜSOY M., PAKDEMIRLI M. Approximate analytic- cal solutions for the flow of a third-grade fluid in a pipe[J]. International Journal of Non-Linear Mechanics, 2002, 37(2): 187-195.
[6] ELLAHI R., HAYAT T. and MAHOMED F. M. et al. Effects of slip on the nonlinear flows of a third grade fluid[J]. Nonlinear Analysis Real World Applications, 2010, 11(1): 139-146.
[7] BODDINGTON T., FENG C. G. and GRAY P. Thermal explosions, criticality and the disappearance of criticality in systems with distributed temperatures I. Arbitrary Biot number and general reaction-rate laws[J]. Proceedings of the Royal Society A Mathematical Physical and Engi- neering Sciences, 1983, 390: 247-264.
[8] ZATURSKA M. B. Critical conditions for thermal explo- sion in reactive viscous flows[J]. Combustion and Flame, 1981, 41(2): 201-211.
[9] SHONHIWA T., ZATURSKA M. B. Disappearance of criticality in thermal explosion for reactive viscous flows[J]. Combustion and Flame, 1987, 67(2): 175-177.
[10] BRITZ D., STRUTWOLF J. and ØSTERBY O. Digital simulation of thermal reactions[J]. Applied Mathematics and Computation, 2011, 218(4): 1280-1290.
[11] BRIDGES C., RAJAGOPAL K. R. Pulsatile flow of a che- mically-reacting non linear fluid[J]. Computers and Ma- thematics with Applications, 2006, 52(6-7): 1131-1144.
[12] MAKINDE O. D. Thermal stability of a reactive third grade fluid in a cylindrical pipe: An exploitation of Hermite-Pade Hermite-Padé approximation technique[J]. Applied Mathematics and Computation, 2007, 189(1): 690-697.
[13] MASSOUDI M., PHUOC T. X. Flow of a non-linear (den- sity 430-gradient-dependent) viscous fluid with heat gene- ration, viscous dissipation and radiation[J]. Mathematical Methods in the Applied Sciences, 2008, 31(14): 1685- 1703.
[14] AJADI S. O. A note on the thermal stability of a reactive non-Newtonian flow in a cylindrical pipe[J]. Internatio- nal Communications in Heat and Mass Transfer, 2009, 36(1): 63-68.
[15] CHINYOKA T., MAKINDE O. D. Computational dyna- mics of unsteady flow of a variable viscosity reactive fluid in a porous pipe[J]. Mechanics Research Communica- tions, 2010, 37(3): 347-353.
[16] CHINYOKA T., MAKINDE O. D. On transient flow of a reactive variable viscosity third-grade fluid through a cyli- ndrical pipe with convective cooling[J]. Meccanica, 2012, 47(3): 667-685.
[17] IREKA I. E., CHINYOKA T. Non-isothermal flow of a Johnson-Segalman liquid in a lubricated pipe with wall slip[J]. Journal of Non-Newtonian Fluid Mechanics, 2013, 192(2): 20-28.
[18] ADEGBIE K. S. Thermal explosion in a combustible gas mixture with general Arrhenius reaction-rate laws: Critica- lity and its disappearance[J]. Afrika Matematika, 2013, 24(2): 195-208.
[19] OKOYA S. S. On criticality and disappearance of critica- lity for a branched-chain thermal reaction with distributed temperature[J]. Afrika Matematika, 2013, 24(4): 465- 476.
[20] JAYEOBA O. J., OKOYA S. S. Approximate analytical solutions for pipe flow of a third grade fluid with variable models of viscosities and heat generation/absorption[J]. Journal of the Nigerian Mathematical Society, 2012, 31: 207-227.
* Biography: Samuel S. OKOYA (1958-), Male, Ph. D.,Professor
10.1016/S1001-6058(16)60610-8 2016,28(1):84-94
水动力学研究与进展 B辑2016年1期
- 水动力学研究与进展 B辑的其它文章
- Investigation of the effects of platform motion on the aerodynamics of a floating offshore wind turbine*
- Mixing of two different electrolyte solutions in electromagnetic rectangular mixers*
- A new biomimicry marine current turbine: Study of hydrodynamic performan- ce and wake using software OpenFOAM*
- Study of bedload transport in backwater flow*
- Experimental study of water and dissolved pollutant runoffs on impervious surfaces*
- A numerical model for pipelaying on nonlinear soil stiffness seabed*
