OFDM低压电力线噪声抑制仿真研究

罗君卿，谭周文

(湖南人文科技学院 信息学院，湖南 娄底 417000)



OFDM低压电力线噪声抑制仿真研究

罗君卿，谭周文

(湖南人文科技学院 信息学院，湖南 娄底 417000)

电力线信道中存在的脉冲噪声是引起信号衰减的主要因素,电力线信道中的噪声不可以简单地描述为加性高斯白噪声。消除脉冲噪声最常用的的方法是通过在OFDM接收器之前采用限幅或者消隐的非线性处理器来进行处理。通过仿真验证了传统的非线性消隐对电力线信道中的脉冲噪声的抑制作用，采用一种新的脉冲噪声抑制方法——自适应阈值区间消隐技术，可在传统消隐的基础上进一步降低系统的误码率。

电力线通信；消隐；脉冲噪声抑制；自适应阈值区间

OFDM是多载波传输的一种特殊情况，单个的数据流在许多较低速率的子载波中进行传输。OFDM不仅是一种调制技术，同时它也是一种复用技术。使用OFDM技术最重要的一个原因就是，它能够增加抗频率选择性衰落和窄带干扰的稳定性。在单个载波系统中，单个的衰落或者干扰，都会造成整个链路的失效。但是在多载波系统中，只有少数的子载波会受到影响，纠错码可以用来纠正那些少数的错误的子载波。使用并行数据传输和频分复用技术的概念在1960年代中期提出,一些更早的研究可以追溯到1950年代。

正交这个词揭示了OFDM系统中各个载波之间精确的数学关系。在一般的频分复用系统(FDM)中，许多载波都以一定的间隔隔开，这样就可以使用传统的滤波器和解调器接收信号。在接收器中，不同的载波之间使用保护带宽，可是在频域中，这会导致频谱利用率的下降。所以，我们可以排列OFDM信号中的载波，让各个载波的旁带相互重叠，而且这些信号被接收时会没有相邻的载波的干扰,要想做到这一点，载波必须是正交的。

影响电力线传输的最主要的因素是衰减、多径衰落和噪声。在电力线中总共发现有5种类型的噪声：彩色背景噪声、窄带噪声、与主频异步的周期性脉冲噪声、与主频同步的周期性脉冲噪声、异步脉冲噪声。

一　电力线通信系统模型

(一)OFDM系统

正交频分复用技术是一种多载波传输技术，它能够很好地抑制电力线信道中的多径衰落和频率选择性衰落。在正交频分复用技术中，一行高速的数据流被分成多个并行的低速的数据流，这些数据流通过离散傅里叶逆变换携带在复用的正交子载波上。正交频分复用较长的符号周期使得信号的多径传播造成的符号间干扰所产生的影响降低到最小。离散时间的正交频分复用信号的数学表达式如式(1)：

(1)

式(1)中：N是子载波的总数，Sk是一个正交调幅的符号序列。为了消除信道间干扰和符号间干扰，正交频分复用采用循环前缀加在OFDM信号的最前面。

(二)电力线信道模型

为了在电力线信道中成功传输数据，实际和实用的电力线信道传输数据的模型是必不可少的。Zimmermann和Dostert提出了适合描述电力线信道传输的具有实际意义的信道模型,这种模型基于真实的电力线网络的实际测量数据提出。它由信道传输的功能函数所给出[1]，见式(2)。

(2)

式(2)中：Mw是多径的总数，Ck和Yk分别是权重因素和kth路的长度,与频率相关的衰减是由参数b0、b1和u来模拟的。在该模型中，第一个指数代表在电力线信道中的衰减,而第二个指数用传输速度vw来描述回声情形,4径模型的衰减参数包含在使用的实际测量数据中。我们采用该模型来仿真和研究消隐，减轻在实际的电力线系统中的脉冲噪声。

(三)脉冲噪声

我们知道要想用一种确定的数学模型来描述电力线噪声是很困难的。本文利用加性高斯白噪声的模型模拟背景噪声，利用一个以一定概率出现噪声的泊松过程乘以一个高斯过程，来得到脉冲噪声。因为脉冲噪声是随机出现的，在整个传输信号上，脉冲噪声就会以一定的概率出现，分为轻度、中度、重度3种情况。由于脉冲噪声的幅值符合高斯噪声的特点，再将脉冲噪声与加性高斯白噪声相加，得到信道的噪声模型。在电力线环境中，数据传输可能包含不同种噪声,它们是彩色背景噪声、窄带噪声、与主频异步的周期性脉冲噪声、与主频同步的周期性脉冲噪声和异步脉冲噪声，这5种噪声可以进一步归纳成2种主要类型：背景噪声和脉冲噪声。为了分析它们在基于OFDM的低压电力线系统的影响，背景噪声(ωk)用均值为0，方差为σω2的加性高斯白噪声来表示，脉冲噪声(bk)由式(3)给出[2]：

bk=ckdk

(3)

式(3)中：Ck是指根据泊松过程生成的脉冲噪声，dk是均值为0，方差为σi2的白噪声过程。该白噪声的过程代表脉冲噪声的幅度，这就意味着脉冲噪声的到来服从一个速率为每秒u个单元的泊松分布。这样在1秒钟内脉冲噪声i次到达的概率是：

(4)

另一方面，脉冲噪声的幅度还服从均值为0，方差为σω2的高斯分布，脉冲幅度也被认为是高斯的。

泊松-高斯分布[3]是一种简单、有效的脉冲噪声模型,在本文中采用泊松-高斯分布模型对脉冲噪声建模。在泊松-高斯分布模型中，脉冲噪声的出现由泊松过程给出，脉冲噪声的幅度根据一个均值为0，方差为σω2的高斯过程建模。这个泊松-高斯模型在物理上可以被看作每一个传输的符号都被一个有着概率为Ck，随机高斯幅度为dk的脉冲所干扰。

图1表示的就是脉冲噪声与加性高斯白噪声混合的MATLAB仿真图,其中电力线信道中的背景噪声用加性高斯白噪声来替代。

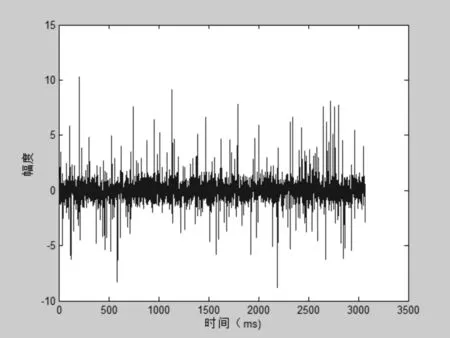
图1　脉冲噪声与加性高斯白噪声混合

二　电力线噪声抑制

对于脉冲噪声的消除方法，一般采用固定门限值限幅或者消隐技术(限幅、消隐和限幅/消隐)来消除脉冲噪声，这些方法虽然简单，但是十分有效。在传输的一端，一个随机信号被映射成QPSK/BPSK信号，然后使用有64个子载波的OFDM系统进行调制；调制后的信号再通过一个给定参数的4径电力线信道，电力线信道中的脉冲噪声被假定服从给定的泊松分布，脉冲噪声和背景噪声被加到OFDM信号上。在接收的另一端，收到的信号rk首先被剪切掉；再使用一个FFT单元进行处理；信号再接着解调，最终保留BER的性能(见图2)。

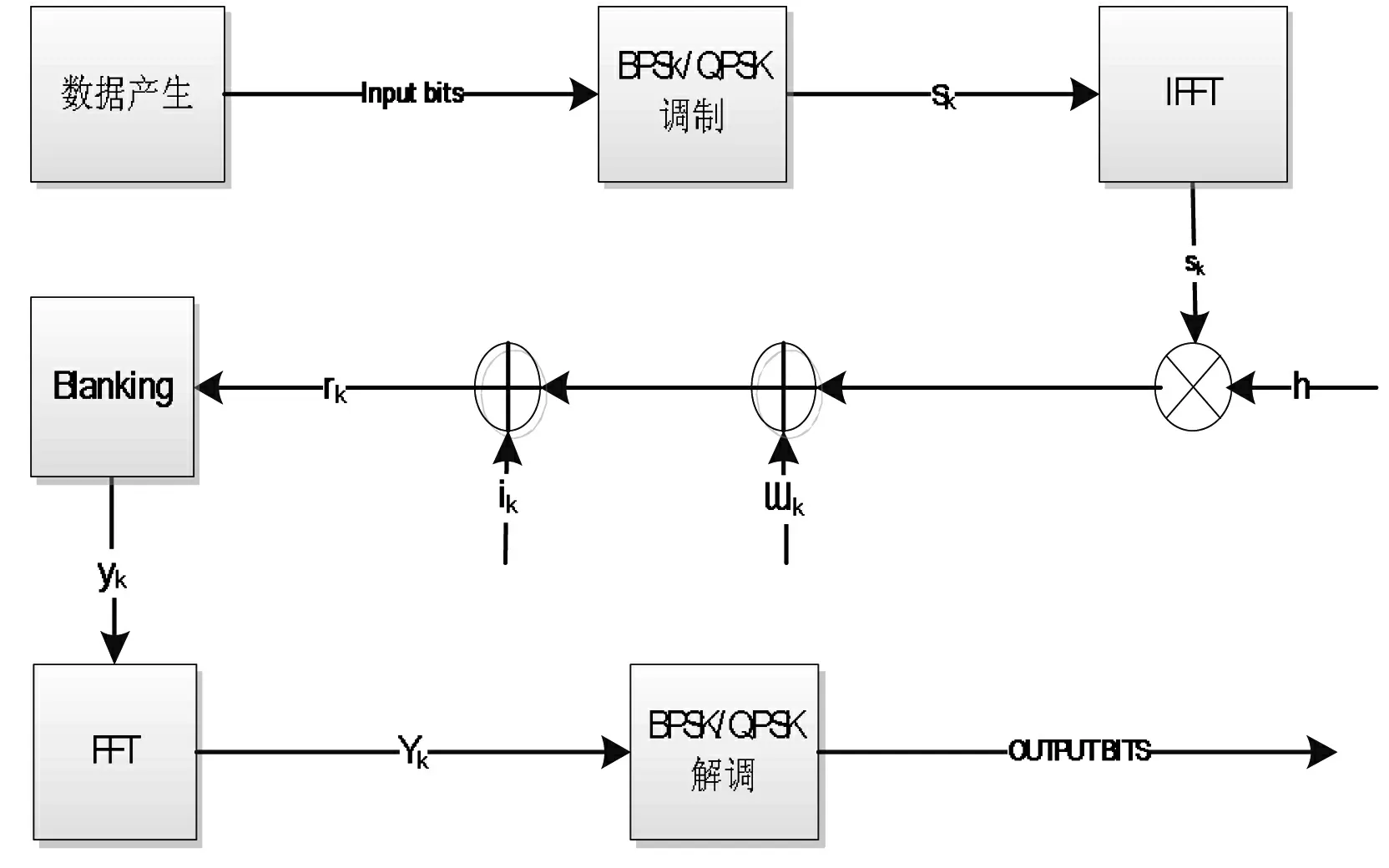
图2　采用消隐模块的电力线系统流程图

图2中Sk是传输的OFDM信号，接收信号在假设有很好的同步的情况下，经过下变频变换，模数转换可以表示如下：

rk=Sk*h+ωk+ikk=0,1,2...N-1

(5)

式(5)中h是电力线信道的快速傅里叶逆变换脉冲响应，*表示卷积。

接下来的仿真均是在轻度、中度、重度等3种不同程度的脉冲噪声情况下进行的。我们是通过控制脉冲噪声概率大小来决定脉冲噪声的轻度、中度、重度情况。

采用抑制脉冲噪声的方法是时域方法，脉冲噪声对于多载波信号的影响可以通过在接收器之前使用非线性消隐或限幅的方法来预处理时域信号，从而降低脉冲噪声对系统的影响。传统意义上的脉冲噪声的幅值很大，因而采用这种时域方法很有效。由于非线性技术非常简便，因此在实际的应用中通常有blanking、clipping、hybrid 3种方法。这些技术是基于这样一种设想提出的，那就是脉冲噪声的幅度比信号的幅度要大到可以分辨出来。而且用于剪切的门限值是固定的，如果有信号的幅值超过了门限值，那么就认为这个信号是受到了脉冲噪声的影响。因此，可根据非线性技术进行调整。

采用固定门限值消隐技术消除脉冲噪声对电力线载波通信系统的影响，消隐模块被放于OFDM接收机之前，也就是一定要保证在FFT之前进行消隐处理，所以本文采用的消隐技术处理是在时域中进行的。固定门限值消隐的方法只改变信道传输信号的幅值，而不改变其相位，数学公式如下[4]：

(6)

式(6)中：Tb是消隐的门限值。我们使用MATLAB来研究在3种不同程度的噪声环境下，OFDM电力线系统消隐后的性能。如果接收到的离散信号的某些点的幅值超过了给定的门限值，那么我们就将这些点重新赋值为0，即消掉这些点的幅值。如果离散信号的某些点的幅值并没有超过给定的门限值，那么我们就保留这些点的值，不做任何处理。

图3—5表示的是受到背景噪声和脉冲噪声干扰的OFDM低压电力线系统采用传统非线性消隐技术后，系统的误码率性能的变化。我们可以明显地观察到在BPSK调制下，分别在轻度、中度、重度3种噪声的情况下，采用传统非线性消隐，系统的误码率都得到了比较大的改善。

图3　轻度噪声下的系统误码率性能对比

图4　中度噪声下的系统误码率性能对比

图5　重度噪声下的系统误码率性能对比

三　自适应阈值区间消隐研究

事实上，最佳门限值在消隐的整个过程中是不断变化的，也就是说最佳门限值随着信噪比的不同而不同，因而传统的固定门限值消隐并不是十分精确，这种抑制脉冲噪声的方法还有很大的改进空间。所以本文基于此提出一种更加精确地抑制脉冲噪声且效果更好的新的自适应阈值区间消隐算法。自适应阈值区间消隐算法通过编程，让计算机根据不同的信噪比情况从一个给定的阈值区间中自动寻找到该信噪比情况下所对应的最佳门限值，然后每次都可以找到一个最佳的门限值用来消隐，使得系统的误码率得到进一步的下降。

图6表示的是中度脉冲噪声下，误码率随着门限值的改变而改变的情形。我们可以看到，对于非线性消隐来说，始终存在着一个最佳门限值，并且这个最佳门限值随着信噪比的不同而不同[5]。

图6　中度脉冲噪声下,不同信噪比下不同门限值所对应的误码率性能

因此我们提出一种新的自适应阈值区间消隐的算法，使得系统总有最小的误码率。图7-9分别表示的是在BPSK调制下，轻度、中度、重度3种噪声情况下，OFDM低压电力线系统均采用自适应阈值区间消隐后，系统的误码率性能的变化。我们可以明显地观察到在轻度、中度、重度3种噪声的情况下，采用自适应阈值区间消隐后，系统的误码率比采用传统消隐，得到了进一步改善。

图7　轻度噪声下系统的误码率性能的变化

图8　中度噪声下系统的误码率性能的变化

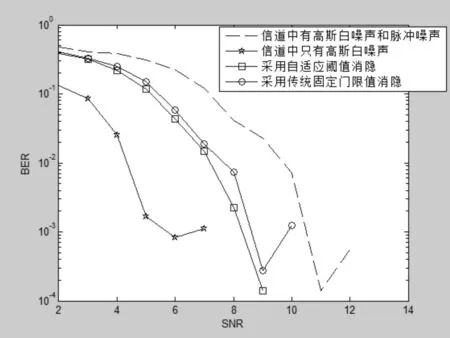
图9　重度噪声下系统的误码率性能的变化

四　不同调制方式下自适应阈值区间消隐误码率性能对比

前面我们仿真出在BPSK调制下，采用自适应阈值区间消隐后，OFDM低压电力线系统的误码率比采用传统的固定门限值消隐，得到了进一步的改善，抑制电力线信道中脉冲噪声的效果更好。下面我们将在采用自适应阈值区间消隐的情况下,列举出在重度脉冲噪声情况下,同时仿真在BPSK、QPSK以及16QAM这3种调制方式下的OFDM低压电力线系统的误码率情况，并把这3种调制方式下的曲线绘制到同一个仿真图里加以比较。最后得出在BPSK调制下，采用自适应阈值区间消隐，OFDM低压电力线系统具有最好的误码率性能,此时系统的误码率是最低的。

图10表示的是OFDM低压电力线系统分别在BPSK、QPSK、16QAM调制下，均采用自适应阈值区间消隐的系统误码率性能对比。我们可以观察到在重度噪声情况下，BPSK调制下的误码率性能好于QPSK调制下，而且QPSK调制下误码率性能好于16QAM调制下。

在重度脉冲噪声的情况下，取一个相同的误码率10-2观察这3条曲线。我们可以得出，当误码率都为10-2的时候，在BPSK调制下，采用自适应阈值区间消隐曲线的信噪比的值为6dB左右；在QPSK调制下，采用自适应阈值区间消隐曲线的信噪比的值为12dB左右；在16QAM调制下，采用自适应阈值区间消隐曲线的信噪比的值为26dB左右。

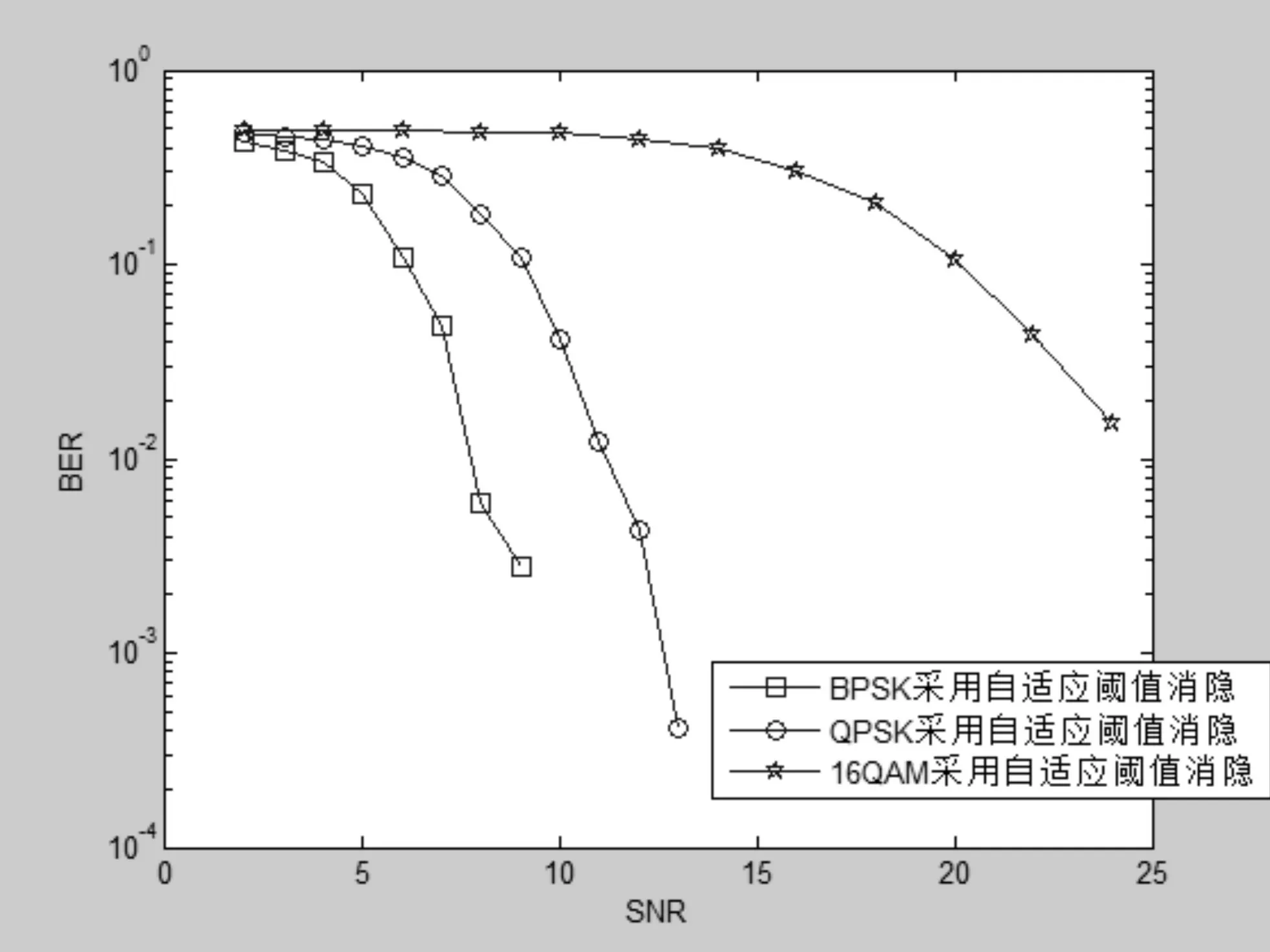
图10　重度噪声下，自适应阈值区间消隐后系统误码率性能对比

五　结论

我们仿真并验证了传统的非线性消隐对电力线信道中脉冲噪声的抑制作用，并且提出了一种新的自适应阈值区间消隐的算法。我们通过计算机仿真，在BPSK调制方式下，分别在轻度、中度、重度3种不同程度的噪声下，对比了自适应阈值区间消隐和传统固定门限值消隐这2种算法，得出自适应阈值区间消隐能够在传统消隐的基础上进一步降低系统的误码率；而要想系统的消隐效果最好，系统应当采用BPSK调制。

[1]KIM Y C,BAE J N.Novel noise reduction scheme for power line communication systems with smart grid applications[J].IEEE International Conference on Consumer Electronics, 2011,10(11): 791-792.

[2]AL-MAWALI K S.Adaptive-threshold clipping for impulsive noise reduction in OFDM-Based power line communications[C].International Conference on Advanced Technologies for Communications, 2009: 43-48.

[3]ZIMMERMANN M，DOSTERT K.Analysis and modeling of impulse noise in Broad-Band powerline communications[J].IEEE Transactions on Electromagnetic Compatibility,2002,44(1):249-258.

[4]MAWALI A.Techniques for broadband power line communications: impulsive noise mitigation and adaptive modulation[J].Power Line Communications,2011:90-92.

[5]ZHIDKOV S V.On the analysis of OFDM receiver with blanking nonlinearity in impusive noise channels[C].International Symposium on Intelligent Signal Processing and Communication Systems, 2004:492-496.

(责任编校：杨丽英)

A Simulation Study of Impulse Noise Reduction in OFDM-Based Low-voltage Power Line Communications

LUOJun-qing,TANZhou-wen

(School of Information Science, Hunan University of Humanities, Science and Technology, Loudi 417000, China)

Impulsive noise in the PLC channel is the major factor that causes signal degradation, and it cannot be simply described as AWGN. The most common technique to remove impulsive noise is preceding the OFDM receiver with clipping or blanking nonlinear preprocessors. Having verified through simulations that the traditional nonlinear blanking method can reduce impulsive noise in the PLC channel, the authors of this paper propose an adaptive-threshold blanking technique for noise reduction, which enhances the performance of PLC systems by reducing bit error rate.

PLC; blanking; impulsive noise reduction; adaptive-threshold values

2016-03-19.

罗君卿(1994—)，男，湖南冷水江人，湖南人文科技学院信息学院2016届本科毕业生；谭周文(1981—)，男，湖南涟源人，湖南人文科技学院信息学院讲师，博士，本文指导老师，研究方向：电力线通信。

TN915.853

A

1673-0712(2016)04-0118-06