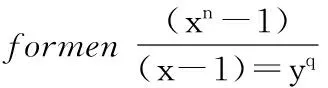关于奇完全数素因数的指标

权双燕

(陕西理工大学 数学与计算机科学学院, 陕西 汉中　723000)



【数理科学·数论专栏研究】

关于奇完全数素因数的指标

权双燕

(陕西理工大学 数学与计算机科学学院, 陕西 汉中723000)

对于正整数a, 设δ(a)是a的所有约数之和。如果正整数n满足δ(n)=2n,则称n是完全数。设n是奇完全数,p是n的素因数,r是p在n的标准分解式中的次数。此时,I(p)=δ(n/pr)/pr称为奇完全数n的素因数p的指标。设q是奇素数,s是正整数。文中运用初等数论方法证明了:如果I(p)=qs,则s是适合s≥22的偶数。

奇完全数;素因数;指标

1　预备知识

设N是全体正整数的集合。对于正整数a,设δ(a)是a的所有约数之和。如果正整数n满足

δ(n)=2n,

(1)

则称n是完全数。由于奇完全数的存在性是数论中长期未能解决的著名难题,所以有关奇完全数的性质一直是引人关注的研究课题[1]。

设n是奇完全数。已知n的标准分解式必为以下形式

n=παp12β1…pk2βk。

(2)

其中π,p1,…,pk是不同的奇素数,α,β1,…,βk是正整数,而且π≡α≡1(mod 4)。这里的π称为奇完全数n的Euler因子。设p是奇完全数n的素因数,r是p在n的标准分解式中的次数。此时

(3)

由于δ(a)是积性函数[2],所以从式(1)和式(3)可得

(4)

(5)

2008年,J. A. B. Dris[3]首先将I(p)称为奇完全数n的素因数p的指标,并且证明了I(p)≥3。此后,文献[4-7]分别给出了I(p)较好的下界。

设q是奇素数,s是正整数。2012年,陈凤娟和陈永高[5]证明了:如果I(p)可表成

I(p)=qs,

(6)

则必有s≥5。最近,付瑞琴和杨海[8]证明了:如果I(p)满足式(6),则s必为适合s≥8的偶数。本文根据高次Diophantine方程的经典结果,运用初等数论方法进一步证明了以下结果:

定 理如果I(p)满足式(6),则s必为适合s≥22的偶数。

2　定理的证明

首先引入两个有关奇完全数和高次Diophantine方程的已知结果:

引理1[9]奇完全数n的标准分解式(2)中的k适合k≥9。

引理2[10]方程

仅有解(X,Y,m)=(3,11,5)和(7,20,4)。

从文献[8]中定理的证明过程可知:如果I(p)满足式(6),则必有

p=π,r=α=1,q=pk,s=2βk,

(7)

其中π是奇完全数n的Euler因子,pk和2βk分别是n的标准分解式(2)中的某个不等于π的素因数及其次数;而且

π+1=2p12β1…pk-12βk-1,

(8)

(9)

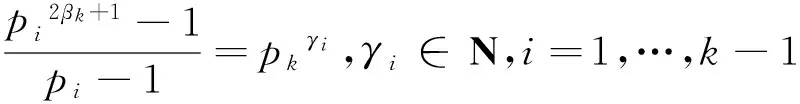
(10)

γ1+…+γk-1=2βk。

(11)

根据上述结果可得以下两个引理。

引理3 式(10)中γi(i=1,…,k-1)都是奇数。

证 明如果式(10)中的某个γj(1≤j≤k-1)是偶数,则从引理2可知

pj=3,βj=2,pk=11,γj=2。

(12)

于是,从式(8)和式(12)可得

(13)

同时,因为pk=11,所以从式(9)可知

1(mod3),

(14)

与式(13)矛盾。由此可知式(10)中的γi(i=1,…,k-1)都是奇数。

引理4如果γj=1(1≤j≤k-1),则βk+1≡0(modpj)。

证 明如果γj=1,则从式(10)可知

所以

pk≡1(modpj)。

(15)

又从式(9)和式(15)可得

2βk+1(modpj)。

(16)

另外,从式(8)可知

π≡-1(modpj)。

(17)

结合式(16)和式(17)可得2βk+2≡0(modpj);又因pj是奇素数,故有βk+1≡0(modpj)。

定理的证明现假定I(p)满足式(6)。已知此时式(7)～(11)成立。

如果γ1,…,γk-1中至少有两个数,设为γj1和γj2(1≤j1

βk+1≡0(modpj1),βk+1≡0(modpj2)。

(18)

因为pj1和pj2是不同的奇素数,所以gcd(pj1,pj2)=1,故从式(18)可得

βk+1≡0(modpj1pj2)。由此可知

βk+1≥pj1pj2≥3×5=15。

(19)

因此,βk≥14,并且从式(7)中最后一个等式可知此时s≥28。

如果γ1,…,γk-1中至多有一个数等于1,则因从引理3可知γ1,…,γk-1都是奇数,所以从式(7)和式(11)可得

s=2βk=γ1+…+γk-1≥1+3(k-2)。

(20)

又因从引理1可知k≥9,故从式(20)可知s≥22。综上所述即得本定理。

[1]GUYRK.UnsolvedProblemsinNumberTheory,thirdedition[M].Beijing:SciencePress, 2007.

[2]华罗庚.数论导引 [M].北京:科学出版社,1979.

[3]DRISJAB.Solvedtheoddperfectnumberproblem:someoldandnewapproaches[D].DeLaSalleUniversity, 2008.

[4]DRISJAB,LUCAF.Anoteonoddperfectnumbers[EB/OL].ArXiv: 1103.1437v3 [math.NT], 2012.

[5]CHENFJ,CHENYG.Onoddperfectnumbers[J].BulletinoftheAustralianMathematicalSoc, 2012, 86(3):510-514.

[6]BROUGHANKA,DELBOURGOD,ZHOUQZ.ImprovingtheChenandChenresultforoddperfectnumbers[J].Integers, 2013,13(A39): 1-8.

[7]CHENFJ,CHENYG.Ontheindexofanoddperfectnumber[J].ColloqMath, 2014, 136(1):41-49.

[8]付瑞琴，杨海.奇完全数素因数的一个性质 [J].西北大学学报(自然科学版),2015,45(1): 14-16.

[9]NIELSONPP.Oddperfectnumbers,diophantineequations,andupperbounds[J].MathComp, 2015, 84(295): 2549-2567.

(编辑亢小玉)

On the index of prime divisors of odd perfect numbers

QUAN Shuang-yan

(School of Mathematics and Computer Science, Shaanxi University of Technology, Hanzhong 723000，China)

For any positive integera, Letδ(a) denote the sum of all divisors ofa. A positive integernis called a perfect number ifδ(n)=2n. Letnbe an odd perfect number, further letpbe a prime divisor ofnandrbe the degree ofpin the factorization ofn. Then,I(p)=δ(n/pr)/pris called the index of prime divisorpof odd perfect numbern. Letqbe an odd prime andsbe a positive integer. By some elementary number theory methods, it is proved that ifI(p)=qs, thensis an even integer withs≥22.

odd perfect number; prime divisor; index

2016-03-11

国家自然科学基金项目(11371291)；陕西省自然科学基金资助项目(2016JQ1041)

权双燕，女，陕西西安人，西北大学数学学院访问学者，从事基础数学的教学与研究。

O156.2

A

10.16152/j.cnki.xdxbzr.2016-03-004