高含水油田含水率预测灰色Verhulst模型优化

管 错　石成方　王继强

(中国石油勘探开发研究院， 北京 100083)



高含水油田含水率预测灰色Verhulst模型优化

管 错石成方王继强

(中国石油勘探开发研究院， 北京 100083)

针对原始含水率数据波动性较大时出现的状况，对灰色Verhulst模型进行优化。改进白化方程初始值选取方法，提高灰色Verhulst模型的预测精度。优化后灰色Verhulst模型预测效果良好，预测高含水阶段含水上升规律时的小误差概率达到100%。

水驱油田； 含水率； 灰色Verhulst模型

含水率上升受多种因素的共同影响，特别是在高含水后期，在储层物性、注采连通状况、储层中流体特征等复杂因素的影响下，含水率随时间的变化规律与各种因素之间的耦合关系变得异常复杂[1-3]。在含水率随时间变化规律的研究中，常用模型有Gompertz[4]、Logistic[5]、Usher[6]等。这些模型均是借鉴经济、信息增产数学模型等理论对含水率进行预测。

本次研究引入灰色理论对含水率进行预测。根据灰色系统理论，以“小样本”、“贫信息”的不确定性系统为研究对象，对“有限”的已知信息进行挖掘开发，提取相关内容，最终实现对系统行为特征、运行规律的有效描述和预测[7-8]。灰色Verhulst模型是一种常用的灰色理论模型，本次研究将对灰色Verhulst模型进行优化，并用于高含水油田含水率随时间变化规律的预测。

1　Verhulst模型机理及优化

Verhulst模型最初由德国生物学家Verhulst提出，在描述生物繁殖规律时，该模型可以用来描述具有饱和状态的“S”形过程。

在油田不同的开发阶段，油田含水率上升特征也不相同。油田见水初期，由于水未形成连续的流动相，因而含水率上升较慢；在中高含水时期含水上升，含水率上升较快；在高含水后期，油相由连续相变为部分连续，再进一步变为非连续相，使得油相渗流能力骤减[9]，含水率上升达到一定水平后，上升速度逐渐趋缓，具有近似于“S”形的发展特征。Verhulst模型适用于含水率预测。

1.1灰色Verhulst模型建模原理

设X(0)为非负序列：

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

其中，x0(k)≥0，k=1,2,…,n。

X(1)为X(0)的1-AGO序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

Z(1)为X(1)的紧邻均值生成序列：

Z(1)=(z(1)(2),z(1)(3),…，z(1)(n),)

其中，z(1)(k)=0.5(z(1)(k)+z(1)(k-1))，k=2,3,…,n。

GM(1，1)幂模型为：

x(0)(k)+az(1)(k)=b(z(1)(k))α

GM(1，1)幂模型的白化方程为：

当α=2时，即可得到Verhulst模型及其白化方程[10]：

x(0)(k)+az(1)(k)=b(z(1)(k))2

由此可知，其白化方程为一阶非线性微分方程。计算模型中参数a、b[11]：

式中：

yN=[x(0)(2),x(0)(3),…,x(0)(n)]T

给定初值[12]：

Verhulst模型白化方程的解为：

1.2灰色Verhulst模型优化

由此得到灰色Verhulst模型的改进形式：

改进后的模型既符合新信息优先的原则，又避免了由于数据误差导致的预测结果失真。

1.3预测精度检验

常用的灰色模型预测精度检验方法有相对误差检验法、关联度检验法、后验差检验法。本次研究选用相对误差检验法与后验差检验法来检验改进后灰色Verhulst模型的预测精度。

(1)相对误差检验法。相对误差检验法是一种逐个进行直观比较的算术检验方法，先将实际数据与预测数据之残差和实际数据相除得到平均相对误差，再根据平均相对误差的大小判断预测结果的精度。

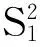
其中：

计算后验差比值C和小概率误差P：

C=S1S2

模型的精度等级可据表1来确定。

表1 模型精度等级表

2　优化后Verhulst模型的实例应用

利用优化后的Verhulst模型预测某油田年综合含水率，取某油田20a间的年综合含水率数据来检验模型预测的精度。

首先对原始序列数据进行初始化，得到原始序列的1—AGO序列，进而得到紧邻均值生成序列，利用紧邻均值生成序列求出相应的Verhulst模型及其白化方程，再运用相关公式计算发展系数和灰色作用量的值。在白化方程求解过程中，运用优化后的模型，分别从紧邻均值生成序列中选取不同的数作为初始值，将其代入相应的白化方程求解。用前述方法对所求结果的预测精度进行检验，可知当初始值为z(1)(3)时模型的精度最高，此时所得到的灰色Verhulst模型为：

以往研究中常用灰色GM(1，1)模型及传统灰色Verhulst模型对油田含水率进行预测。本次研究应用的是优化后的灰色Verhulst模型。

灰色GM(1,1)模型、灰色Verhulst模型、优化后灰色Verhulst模型的含水率预测结果，平均相对误差分别为13.19%、7.88%、3.24%。优化后灰色Verhulst模型的后验差C为0.105 5，小误差概率P为100%，表明该模型精度等级为好。

根据3种模型预测数据绘制图1所示含水率预测状况图。传统Verhulst模型和优化后Verhulst模型所预测的含水率在进入高含水后期后呈“S”形，但优化后Verhulst模型的拟合度更高。优化后Verhulst模型既可避免数据随机性波动带来的影响，又可避免由于数据本身误差所导致的预测结果失真。

图1　3种预测模型的含水率预测状况图

3　结　语

本次研究中，通过对灰色Verhulst模型初始值的优化改进了灰色Verhulst模型的预测精度，并用优化的灰色Verhulst模型进行了油田含水率预测。

与其他灰色系统预测模型结果进行对比，优化后的灰色Verhulst模型预测精度更高。通过改进优化，使模型既符合新信息优先的原则，又避免了由于数据本身的误差导致的预测结果失真。

[1] 俞启泰.水驱特征曲线(5)[J].新疆石油地质，1998，19(3)：233-236.

[2] 林志芳，俞启泰，赵明.水驱特征曲线应用中的问题研究[J].石油勘探与开发，1986(5)：37-44.

[3] 史玉成，盛国强，赵为永，等.水驱开发油田高含水期综合含水率灰色理论预测[J].内蒙古石油化工，2010(10)：60-61.

[4] 王炜，刘鹏程.预测水驱油田含水率的Gompertz模型[J].新疆石油学院学报，2001，12(4)：30-32.

[5] 洪楚侨，杨志兴，苏崇华，等.Logistic曲线在涠洲油田群含水规律研究中的应用[J].海洋石油，2011，31(1)：68-72.

[6] 张居增，张烈辉，张红梅，等.预测水驱油田含水率的Usher模型[J].新疆石油地质，2004，25(2)：191-192.

[7] 张岐山，李志清，肖艳玲.油田含水率的灰色预测方法[J]. 大庆石油学院学报，1997，21(2)：191-192.

[8] 杨华龙，刘金霞，郑斌，等.灰色预测GM(1，1)模型的改进与应用[J].数学的实践与认识，2011，41(23)：39-46.

[9] 刘世华，谷建伟，杨仁锋.高含水期油藏特有水驱渗流规律研究[J].水动力学研究与进展，2011，26(6)：660-666.

[10] 刘思峰，党耀国，方志耕，等.灰色系统及其应用[M].北京：科学出版社，2005：30-35.

[11] 易德生，郭萍.灰色理论与方法：提要·题解·程序·应用[M].北京：石油工业出版社，1992：40-55.

[12] 张大海，江世方，史开泉，等.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002，22(8)：140-142.

OptimizationofGreyVerhulstModelforHighWaterCutOilfield

GUAN CuoSHI ChengfangWANG Jiqiang

(Research Institute of Petroleum Exploration and Development, Beijing 100083, China)

Inthelightoftheinitialwatercut′sfluctuation,animprovedgreyVerhulstmodelmethodisproposed.Byimprovingthechoiceofthewhiteningequationinitialvalue,thepredictionaccuracyofgreyVerhulstmodelisimproved.TheimprovedgreyVerhulstmodelhasgoodeffectonthepredictionofwatercut,andthesmallerrorprobabilityofthewatercutrisingrulecanreach100%inthehighwatercutstage.

waterdriveoilfield;watercut;grayVerhulstmodel

2015-12-08

国家科技重大专项“剩余油分布综合预测与精细注采结构调整技术”(2011ZX05010-002)

管错(1989- )，男，硕士研究生，研究方向为油藏数值模拟。

TE155

A

1673-1980(2016)04-0039-03