基于CGCS2000椭球的城市坐标系建立及应用

兰志武

(福州市勘测院　福建福州　350001)



基于CGCS2000椭球的城市坐标系建立及应用

兰志武

(福州市勘测院福建福州350001)

简要介绍了建立独立坐标系的常用方法，提出了采用“平移、旋转、无缩放”方法，建立基于CGCS2000椭球的城市地方坐标系。同时，描述了新坐标系统的应用以及新坐标系统与国家(地方)坐标系的相互转换关系，实现现有测绘成果与新坐标系统的准确转换。

CGCS2000；地方坐标系；转换精度

0　引言

为了统一城市规划建设布局，需要统一的测绘基准，特别是平面坐标系统。根据文献[1]规定：城市平面坐标系统投影长度变形值不应大于25mm/km，即相对误差小于1/40 000，才能满足大比例尺测图、精密工程建设等需求。本文将以福州市永泰县为例讨论城市地方坐标系的建立方法。

永泰县位于福建省东部，介于北纬25°39′～26°05′，东经118°23′～119°12′，东西长84km，南北宽46km，总面积2 243km2。城区中心距离120°中央子午线约117km，最东边距120°中央子午线约80km,最西边距120°中央子午线约162km；若直接采用120°中央经线作为永泰县区域3°带投影的中央经线，长度变形最大值约32cm/km，最小变形值约8cm/km，超出文献[1]中规定的投影变形不大于2.5cm/km。因此，为了减小投影变形影响、满足国土报批需要等要求，有必要建立新的地方独立坐标系。根据国测国发[2013]11号《关于加快2000国家大地坐标系推广使用的通知》。本文将讨论基于CGCS2000参考椭球的城市地方独立坐标系建立方法及其应用。

1　建立独立坐标系的方法

由文献[2]中相关内容可知，独立坐标系的建立方法大致可以归纳为以下3种：

(1)采用具有高程抵偿面的国家统一3°带高斯投影平面直角坐标系统，其中央子午线与国家坐标系采用的3°带相同，投影面采用高程抵偿面，高程抵偿面一般选择为当地的平均高程面。此种方法保持中央子午线不变，选择某一高程面作为归化高程面，使高程归化改正和高斯投影变形改正相互抵消，使得测区中央的两项投影改正接近于零；

(2)采用自定义中央子午线高斯投影平面直角坐标系统，其投影面采用国家坐标系参考椭球面。此种方法保持高程归化面不变，只移动中央子午线的方法，使得测区中央的两项投影改正接近于零；

(3)采用具有高程抵偿面的自定义中央子午线高斯投影平面直角坐标系统，其投影面一般选择为当地的平均高程面，中央子午线位于城市中心。此种方法以测区中央为中央子午线，归化高程面提高到测区的平均高程面上，建立任意带高斯正形投影平面直角坐标系，这样可以保证测区的两项改正在测区中央几乎为零。

此外，还有采用椭球变换的方法即运用椭球膨胀法、椭球平移法、椭球变形法等建立独立坐标系[5]。各种独立坐标系的建立方法各有其优点、缺点，在实际的应用过程中有其特殊要求。

本文将采用“平移、旋转、无缩放”的方法建立城市地方坐标系，并对其在实际的生产应用中加以介绍。

2　城市地方坐标系的建立

2.1坐标系统的定义

由文献[2]相关规范可知：建立城市平面坐标系统涉及到参考椭球的选择、中央子午线的选择、投影面高程的选择以及坐标系原点和定向的选择等内容。

根据此规范要求，通过对永泰县地理位置、城市建设中长期规划发展状况、以及经济建设状况等因素，综合考虑采用自定义中央子午线高斯正形投影方式建立城市地方独立坐标系，以在城区中央的118°50′为坐标系的中央子午线，投影后平移旋转至中央子午线为120°的1980西安坐标系(尺度比为1)，参考椭球采用CGCS2000坐标椭球，投影面采用CGCS2000坐标系参考椭球面，坐标系原点和定向同CGCS2000坐标系，高程系统采用1985国家高程基准。此方法可以确保长度投影变形不大于2.5cm/km，满足城市测量和城镇地籍调查精度要求等；此外，新建立的城市地方坐标系统即CGCS2000(Y)坐标系采用CGCS2000国家坐标系，坐标形式为中央经线120°的，真正的投影方式为118°50′。

2.2CGCS2000(Y)坐标系控制点成果的获取

在坐标系定义完成后，需要获取在CGCS2000(Y)坐标系下相应的控制点成果，为后续的相关工作提供基础数据(如计算与1980西安坐标系、WGS-84坐标系、CGCS2000坐标系等之间的转换参数)。

按照如下流程获取控制点在新坐标系下的成果：

(1)获取控制点的CGCS2000-118.50和XA80-120坐标，求取CGCS2000-118.50至XA80-120的首次四参数，并解算拟建坐标系初次成果；

(2)将四参数中尺度比设置为1后反复迭代计算择优选取转换参数，解算拟建坐标系CGCS2000(Y)坐标系的最终成果；

(3)计算其他控制点的CGCS2000(Y)坐标系成果用于与其他坐标系转换参数的求解。

2.3CGCS2000(Y)坐标系下投影变形分析

根据上述方法获取了已有控制点成果的CGCS2000(Y)坐标系坐标成果，为了检核投影长度变形是否满足不大于2.5cm/km的要求，采用RTK测量方式实地采集部分控制点的坐标，比较已知控制点间的距离与实测已知控制点间的距离，判断新建坐标系的测量成果是否满足精度要求。投影长度变形实地检核较差统计见表1。

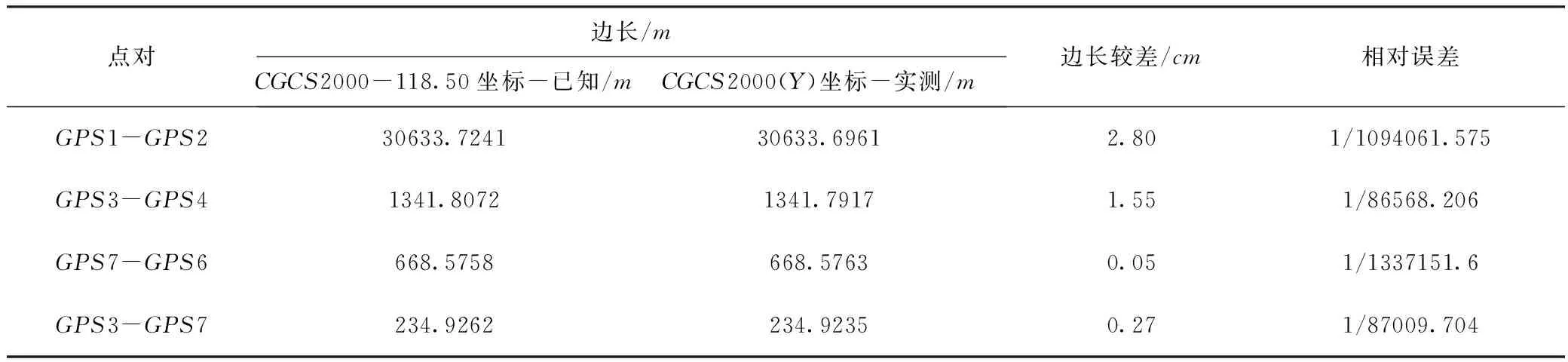
表1　实测(RTK)边长检核较差统计表

由表1可知：边长较差最大值为2.80cm，最小值为0.05cm，相对误差小于1/14000,符合文献[3]中RTK平面控制点检核测量技术要求。

3　CGCS2000(Y)坐标系与国家(地方)坐标系之间的联系

根据文献[2]中相关规范要求，新建立的坐标系应实现与现行的国家坐标系(如CGCS2000坐标系、1980西安坐标系、1954北京坐标系)之间的相互转换，以及城市平面坐标系新、旧网之间的相互转换。

坐标转换工作非常复杂又重要，应本着“最匹配本区域原有平面控制点坐标系统和转换后成果精度损失最小”为原则，对各阶段转换结果进行严格检查和反复验算，每一阶段成果都合格后，成果才能提交使用。

3.1坐标转换数学模型

常用的坐标转换一般包括各种空间直角坐标系与大地坐标系，地心空间直角坐标系与参心空间直角坐标系，以及不同参心空间直角坐标系之间的相互转换。当不同坐标系之间存在严密的数学转换模型时，可以采用相应的模型之间进行坐标转换，目前常采用转换模型有布尔沙模型、三维七参数转换模型、二维七参数转换模型、二维四参数转换模型、三维四参数转换模型等众多转换模型。本文以采用二维四参数转换模型求解CGCS2000(Y)坐标系与CGCS2000坐标系之间的转换参数。

将CGCS2000坐标系坐标按118°50′3度带高斯投影后与CGCS2000(Y)坐标系通过二维四参数转换模型进行转换。

二维四参数转换的模型如下：

式中：

x1，x2——源坐标系坐标，单位为m

x2,y2——目标坐标系坐标，单位为m

Δx，Δy——为平移参数，单位为m

α——为旋转参数，单位为rad

m——尺度参数，无量纲

1980西安坐标系、WGS-84坐标系、1954北京坐标系与CGCS2000(Y)坐标系转换四参数均可按照图2计算流程求解。

3.2精度评定

为了科学、客观地评价计算转换参数的可靠性和准确性，将用于参数计算的重合点代入转换模型，用得到的转换参数计算重合点坐标残差，剔除残差大于3倍点位中误差的重合点，再以剩下的点重新计算转换参数，直到所有参与计算转换参数的点都满足精度要求为止[6]。根据已有点位分布情况，最终选择了等级较高、精度可靠的28个控制点作为求解参数重合点(其中GPSA级点2个、GPSC级点8个、城市三等点18个)，如图4.2所示；以及参数验算重合点分布略图，如图4.3所示。根据图2计算流程，计算CGCS2000(Y)坐标系至CGCS2000坐标系二维转换四参数。鉴于转换参数的保密性，本文没有列举4个转换参数的具体数值。

根据转换前后的坐标数据，进行转换参数的精度评定。具体方法如下：

V(转换残差)=重合点转换坐标值-重合点已知坐标值

式(1)

利用式(4.2)计算各平面点转换误差M点：

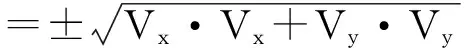
式(2)

同时，利用式(4.3)评定转换参数转换精度：

式(3)

式中，MX为X方向转换中误差，MY为Y方向转换中误差，

则可以利用式(4.4)计算转换中误差M：

式(4)

根据上式计算、统计采用二维转换四参数的X方向转换中误差、Y方向转换中误差以及转换中误差等精度指标。限于篇幅，文中只列举了部分参数验算重合点的转换误差，具体见表2和表3。

表2　二维四参数转换误差(部分)

表3　二维四参数转换精度统计表

由表2、表3统计结果可知，二维转换四参数转换结果中，求解参数重合点点位误差最小值为0mm，点位误差最大值为1.1mm，点位中误差为0.5mm，满足规范要求的参数计算重合点的点位误差小于3倍点位中误差；对于参数验算重合点点位误差最小值为0.3mm，点位误差最大值为1.1mm，点位中误差为0.4mm，转换精度较高。

此外，结合表2和图5、图6曲线走势可以看出，求解参数重合点在x方向转换误差均在1mm以内，96%的点在y方向的转换误差及转换中误差均在1mm以内；参数验算重合点在x方向转换误差均在1mm以内，99%的点在y方向的转换误差均在1mm内，98%的点转换中误差均在1mm以内，转换精度比较高。

3.3CGCS2000(Y)坐标系的应用

在新坐标系统建立完成后，不但要建立新坐标系统与原有坐标系统的转换关系，实现现有测绘成果与新坐标系统之间相互精确转换，而且还要规范新坐标系统的使用。因此，在新坐标系使用过程中要注意以下四点：

(1)除国土用地报批特殊要求外，城市规划、工程建设、勘测定界等工作均在新的坐标系统下实施完成；

(2)工程放样：利用相应的转换参数(如1980西安坐标系至CGCS2000(Y)坐标系转换四参数)将设计坐标转换至CGCS2000(Y)坐标系，采用CGCS2000(Y)坐标进行放样；

(3)日常控制测量平差计算(用于GPS静态解算)：平差计算应放在投影经线为118度50分下进行，投影高为0；无约束平差后，输入已知平面控制点时，已知点东西方向加上*米后参与计算，投影设置选择118度50分，待平差后东西方向坐标成果减去*米；

(4)针对国土用地报批的地块，建立新坐标系统与西安80坐标系的转换关系，实现用地红线由新坐标系统向西安80坐标系的转换(面积不变)，满足国土用地报批需求。

4　结语

本文以永泰县为例，讨论了基于CGCS2000椭球建立城市地方坐标系统的过程，根据永泰县的具体情况确定了相应的建立方案，并建立了新坐标系统与国家(地方)坐标系统联系。根据转换精度可知，转换结果准确、可靠，可以用来实现已有测绘成果与新坐标系统之间相互转换，而且不会造成精度的损失。

此外，新坐标系统的建立解决了长度变形问题带来的困扰，有利于提高测绘成果的精度，更加简单方便地获取可靠的高精度成果。同时，将已有各种坐标系统的测绘成果统一到新坐标系统下，解决了多种坐标成果资料混乱问题，为日常工作中测绘成果的使用提供了方便。

[1]CJJ/T8-2011 城市测量规范 [S]

[2]GB/T28584-2012 城市坐标系统建设规范 [S]

[3]CJJ/T73-2010卫星定位城市测量技术规范[S]

[4]李东,毛之琳.基于CGCS2000的地方坐标系统建立方法的研究[J].测绘技术装备，2009(4):3～5

[5]海清.通过椭球变换建立区域独立坐标系的方法[J].海洋测绘，2007(9)：31～34

[6]大地测量控制点坐标转换技术规程[M].北京：国家测绘地理信息局，2013.

兰志武(1967.1-)，高级工程师，主要从事测绘与地理信息工程。

OntheEstablishmentandApplicationofCityCoordinateSystemBasedonCGCS2000Ellipsoid

LAN Zhiwu

(FuZhouInvestigationandSurveyingInstitute,Fuzhou350001)

Inviewoftheexistingproblemsofurbancoordinatesystem,thispaperbrieflyintroducesthecommonmethodsofestablishingindependentcoordinatesystemandputforwardthe"translation,rotation,noscaling"methods,andestablishesurbanlocalcoordinatesystembasedonCGCS2000ellipsoid.Atthesametime,thispaperdescribestheapplicationofthenewcoordinatesystem,andthemutualchangerelationofnewcoordinatesystemwiththenational(local)coordinatesystem,achievesaccurateconversionofexistingsurveyingandmappingresultsandthenewcoordinatesystem.

CGCS2000；localcoordinatesystem；TransformationAccuracy

兰志武(1967.1-)，高级工程师。

E-mail:610428934@qq.com

2016-02-10

TU198

A

1004-6135(2016)03-0109-05