基于NNIA的工程项目工期-成本-质量综合优化

金　成

(深圳市东方银座集团有限公司　广东深圳　518040)



基于NNIA的工程项目工期-成本-质量综合优化

金成

(深圳市东方银座集团有限公司广东深圳518040)

工期、成本、质量是工程建设项目的三大控制目标。当前工程管理人员对三大目标的控制相对独立，不能高效地对三大目标进行综合控制。为了更好地解决三大目标之间的协调问题，结合系统可靠性原理，利用二元决策图(Binary Decision Diagram，BDD)对工程项目的整体质量水平进行评价。同时，考虑工程实际的奖罚制度，构建工期-成本-质量综合优化模型并运用非支配近邻免疫算法(Non-dominated Neighbor Immune Algorithm，NNIA)进行求解。运算结果得到了一系列Pareto最优解，验证了所构建模型的可行性及NNIA对求解该模型的有效性。

工程项目；工期-成本-质量综合优化；质量可靠性；非支配近邻免疫算法(NNIA)；二元决策图(BDD)

0　引言

工期、成本、质量三大目标之间是相互影响相互制约的，改善其中一个目标将会以其他目标为代价。随着工程项目的大型化、复杂化，工期、成本和质量的综合优化研究也越来越被关注。当前对于工期-成本-质量综合优化问题的研究主要集中在以下三个方面：

(1)质量的量化

Babu等[1]以0至1之间的数值表示各工序的质量水平，并将各工序质量水平的算数平均值作为工程项目的整体质量水平。El-Rayes等[2]对每项工序设定相应的质量评定指标，通过加权平均得到各工序的质量水平。Pollack-Johnson等[3]运用层次分析法对各个工序的质量水平进行评价。张连营等[4]结合混联系统可靠度理论对工程项目的整体质量水平进行评价。

(2)综合优化模型的构建

对于工期-成本-质量综合优化模型的构建，Babu等[1]提出了三者之间的线性规划模型。Pollack-Johnson等[3]提出了离散型模型。王健等[5]结合多属性效用函数构建了工期-成本-质量综合优化模型。杨耀红等[6]利用模糊多属性群决策效用函数理论，构建模糊综合优化模型。Ghodsi等[7]为了将模型更好运用于工程实际，提出了连续非线性综合优化模型。

(3)模型的求解方法

运用智能优化算法来对综合优化模型进行求解是当前的一个研究热点。随着计算机技术与智能优化算法的发展，研究人员已经将遗传算法[2]、蚁群算法[8]、微粒群算法[9]、Pareto蚁群算法[10]等运用于工程多目标问题的求解。

当前对工程项目质量水平的评价方法大多没有充分考虑各工序之间的逻辑关系，本文基于系统可靠性理论，结合二元决策图(BDD)对工程项目的整体质量水平进行评价，同时引入对求解高维多目标问题有较大优势的非支配近邻免疫算法(NNIA)，对所构建的综合优化模型进行求解，从而使得模型求解能够更高效。

1　模型构建

1.1工期目标

对于工期的计算，可以依据关键路径法来求得，工期目标的函数可由式(1)表示：

(1)

其中，T表示工程项目的总工期，Lk表示施工网络图中第k条路径，L表示施工网络图中的所有路径。

1.2质量目标

工程项目的整体质量水平是由工程项目所包含的各个工序的质量水平决定。通常情况下，工序作业时间在正常完工时间的基础上缩短，工序的质量水平将会降低；而工序作业时间在正常完工时间的基础上延长，工序的质量水平并不会明显提高。为了便于对工序质量水平进行评价，在此以0～1之间的任意实数来表示每道工序的质量水平。

由此，得到工序作业时间与质量水平之间的关系图，如图1所示：

假设最长完工时间tlij下工序的质量水平为1。在此借鉴赵瑞等[11]所提出的工序作业时间与质量之间的关系模型，如式(2)所示：

Qij=ln(aij*tij+bij)

(2)

s.t.tsij≤tij≤tlij(i,j)∈A

系数aij和bij可以由以下两个式子计算得到：

其中，Qij表示工序(i，j)在作业时间为tij时的质量水平，qij表示工序(i，j)的最低质量要求水平，公式中其他字母和符号意义同前。

获得各个工序的质量水平之后，本文依据可靠性理论，将工程项目视为一个系统，根据网络系统可靠性的计算方法，引入二元决策图(BDD)来计算工程项目的整体质量水平。BDD是布尔函数的一种图形表达方式，可以直观地反映出函数的逻辑结构，具有很高的计算效率，并方便计算机实现。

运用BDD算法对网络系统可靠度的求解可以由以下几个步骤进行[12]：

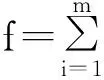
(2)将f用BDD表示；

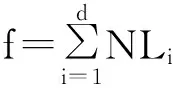
(4)网络系统的可靠度可以依据各边的概率由式(3)计算得到：

(3)

其中，Li表示第i条最小路集各边的乘积形式，Prob表示求概率值。

为了描述方便，在此用函数R=F(xi)作为BDD算法计算系统可靠度的函数表达式，即因变量R表示系统可靠度，自变量xi表示网络系统中各工作单元(子系统)的可靠度。则基于BDD算法改进后的质量目标的函数可由式(4)表示：

Q=RQ=F(Qij)=F[ln(aij*tij+bij)]

(4)

其中，Q表示工程项目整体质量水平，RQ表示质量可靠性，公式中其他字母和符号意义同前。

1.3成本目标

工程成本包括直接成本和间接成本。在施工条件不变的情况下，工序的直接成本会随着工序作业时间的缩短而增加。由于工序作业时间的压缩将会使得工程资源如劳动力、施工机械以及周转材料等投入量的相应增加。当工序作业时间延长时，工序的总资源投入量并不会减少，反而可能造成工人窝工以及施工机具闲置，从而使得工序直接成本增加。另一方面，如果工序作业时间压缩，现场固定资产使用费、管理人员的工资等工程间接费将会减少。因此缩短工序作业时间将会降低工序的间接成本，相应地延长工序作业时间也将会增加工序的间接成本。

基于上述分析，工序作业时间与成本之间的近似关系可用图2进行表示。

假设每道工序都有一个最长完工时间tlij和最短完工时间tsij。在此引入张连营等[4]所提出的带成本递增因子的工序时间与成本之间的二次函数模型，如式(5)所示：

Cij=Cnij+αij(tij-tnij)2

(5)

其中，Cij表示工序(i，j)的实际成本，Cnij表示工序(i，j)在正常作业时间下的完工成本，tij表示工序(i，j)的实际作业时间，αij表示工序(i，j)边际成本递增因子。

在工程实际中，建设单位会设定相应的合同工期Tc。对于延期完工的项目，建设单位往往会对施工单位进行罚款。而有些项目如果缩短工期，将使项目提前投入使用，及早发挥效益并收回投资，施工单位也可能因为工程提前完工而受到奖励。同时，对于能够实现质量评优目标的工程，施工单位往往会受到相应的奖励。当工程未能实现质量评优目标，施工单位也可能受到相应的惩罚。工程项目的总成本可以由项目所有工序的成本求和所得。由此，以施工单位的角度，考虑了奖罚制度的成本目标函数可由式(6)表示：

(6)

其中，C表示工程项目总成本，Cij表示工序(i，j)的实际成本，Cnij表示工序(i，j)在正常作业时间下的完工成本， A表示工程项目所有工序的集合，δ表示工程延期的惩罚系数，ε表示提前完工的奖励系数，Td表示工程延期天数，Ts表示工程提前完工天数，ω为质量惩罚系数，τ为质量奖励系数，q表示工程项目评优要求的质量水平，公式中其他字母和符号意义同前。

1.4工期-成本-质量综合优化模型

基于上述分析，将公式(1)、(4)和(6)综合起来，即可得到工程项目工期-成本-质量综合优化模型，如式(7)：

(7)

式中

s.t.tsij≤tij≤tlij(i,j)∈A

公式(7)表示以工程各工序的作业时间为自变量对工程的工期、成本和质量目标进行权衡考虑，寻求最优决策组合。

2　NNIA对模型的求解

Gong等[13]所提出的非支配近邻免疫算法(Non-dominatedNeighborImmuneAlgorithm，NNIA)对求解高维多目标优化问题具有较大的优势[14]。本文采用MATLAB软件实现算法编程，模型的求解主要有以下几个步骤。

2.1初始参数的确定

在模型的求解中，以各工序的实际作业时间tij为决策变量Tij。设定模型的变量维数E=m，m表示工程项目所包含的所有工序的数目，则可行域为[bd，bu]E。其中bd =[ts12,…,tsij]为决策变量的下限，表示各个工序的最短完工时间，bu=[tl12,…,tsij]为决策变量的上限，表示各个工序的最长完工时间。

2.2抗体种群初始化

NNIA是在既定空间内和相关约束条件下对最优解自动搜索的算法。在此，需要给算法设置一个初始抗体种群。初始抗体种群的抗体是依据优势种群规模上限nd在可行域的空间内随机产生的。在工期-成本-质量综合优化模型中，初始抗体种群中的解所表示的是在可行域的范围内随机产生的各个工序的作业时间。

2.3免疫操作

这部分的操作包括拥挤距离计算、比例克隆、重组和超变异以及非支配近邻选择。拥挤距离是对在目标空间中以最近邻个体作为顶点构成的矩形的周长的衡量，是区分优势种群中抗体的优劣的标准。比例克隆是指具有较大拥挤距离值的个体将会更多次地被复制，从而使前端上的个体分布较稀疏的区域将有更多的机会被搜索。基于拥挤距离计算及比例克隆使得优势种群得以更新。重组和超变异操作是为了防止算法出现“早熟”问题，陷入局部最优解。对于非支配近邻选择，在NNIA中，优势种群作为外部种群实现了精英保留策略。选择操作倾向于具有高拥挤距离的个体。只有部分具有高拥挤距离值的非支配个体被选中。克隆、重组、变异只适用于被选中的个体。由此，在一代内，只有部分拥挤距离较大的个体进行启发式搜索，从而获得更多位于较稀疏区域的解。

2.4终止及输出

通过上述几个步骤后，当迭代次数g达到所设定的最大迭代次数Gmax，算法终止，输出结果。根据所设的优势种群规模，运算结果将会输出与其对应数量的Pareto最优解，即包含工期、成本和质量目标的决策组合。同时，算法将运算结果得到的Pareto最优解集以图形的形式输出，即可得到工期-成本-质量综合优化的Pareto三维散点图。通过三维坐标图能够直观地观察到所得到的Pareto最优解的分布情况。

3　算例分析

3.1工程概况

以某项目的主体结构工程为例。合同工期105d，合同规定，工程若延期，则每天索赔1.5万元；如果工程被评为省级优良工程(假设项目的总体质量水平达到0.8以上)，则奖励该工程造价的2.0%。案例中含有13个工序，各个工序之间的相互关系和相关参数如表1所示，项目的网络计划图如图3所示。

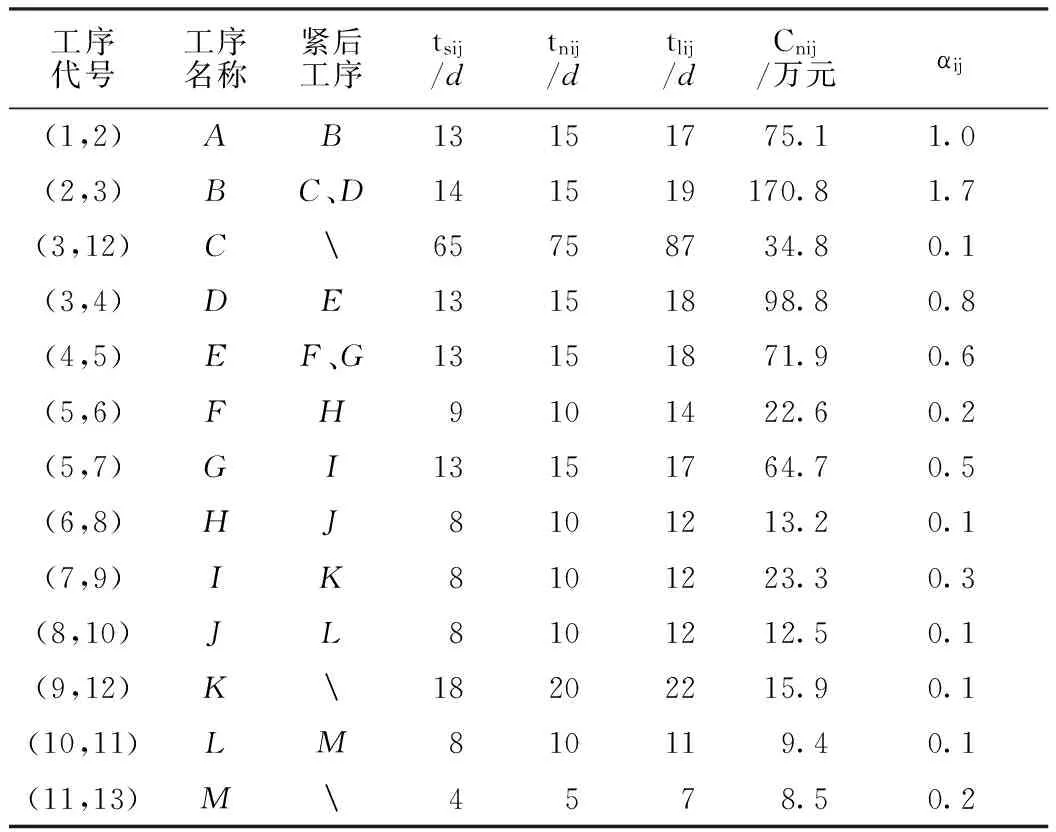
表1　工序相互关系及各参数值

表中的数据是项目部进行网络优化时所使用的数据，αij可以通过分包商的投标标价统计得出。假设各工序在正常完工时间下的质量水平为0.87。

对工程项目进行优化的有效方法是通过组织措施的改进，从而改善工程的控制目标。若要对本工程进行综合优化，则可以先合理安排流水组织作业、采取技术措施、改变施工方法等，进而安排各工序的作业时间及资源投入。但这些组织措施只有通过人为制定才能实现，而所构建的工期-成本-质量综合优化模型的优化结果只能在不改变组织关系的前提下得到。因此，在假设工程项目各工序的组织关系及措施不变的情况下，将本项目的优化问题转化为如何合理安排各工序的作业时间使工程尽可能得实现质量最高与成本最低。

3.2模型求解及分析

运用NNIA对模型进行求解，NNIA算法参数设置如下：优势种群规模上限nd为100；活性种群规模上限na为20；克隆种群规模nc为100；重组概率pc=0.8；模拟二元交叉的分布指数ηc=15；变异概率pm=1/m，其中m为变量的维数，在算例中，工程项目有13道工序，故在该模型中m取13。模型通过MATLAB软件编程，当函数迭代1 000次时，算法停止运行，得到100组Pareto最优解，每个最优解都代表一个工期、成本和质量目标的决策组合，选取其中8个样本，如表2所示。工期-成本-质量综合优化的Pareto前沿的三维散点图如图4所示。

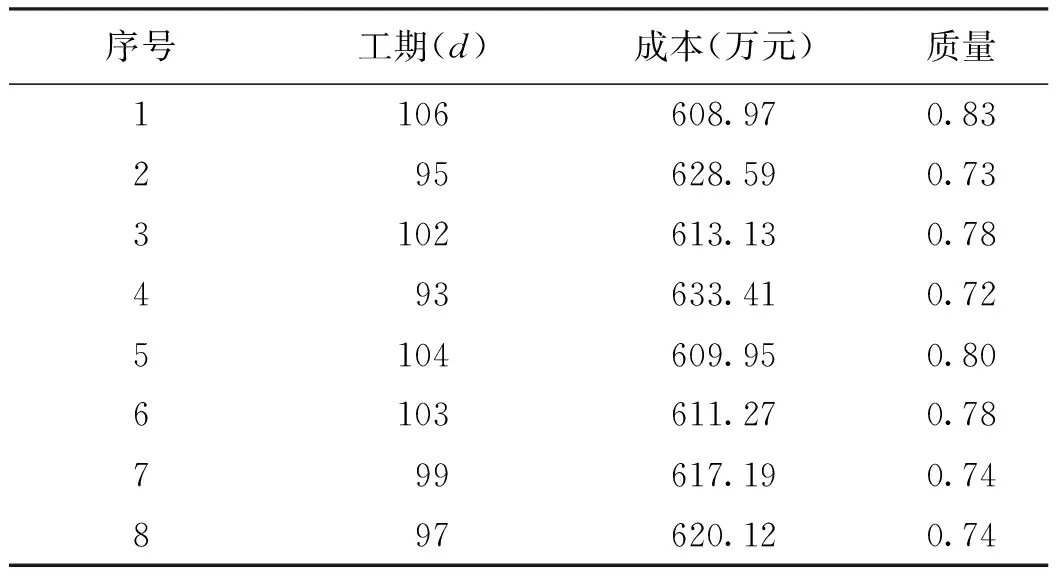
表2　工期-成本-质量综合优化Pareto解示例

如图4所示，所求得的Pareto解的分布近似为一个曲面，趋向于工期最短，成本最低和质量最优的最高目标，在三个目标值权衡中获得综合优化效果。在所得到综合优化结果中，项目决策者可以依据工程实际考虑对三个目标的偏好，选取最符合实际需要的，同时能保证工程正常有序进行的优化组合作为项目管理的参考方案。

例如，通过模型优化，项目管理人员希望质量目标最优，则可在优化结果中选择质量最优的优化组合。通过排序选择，优化结果中的最高质量水平为0.83，相应的优化组合为(T，C，Q)=(106，608.97，0.83)，即工程质量水平为0.83，与之对应的工期和成本分别为106d和608.97万元。

确定优化组合之后，可以依据MATLAB软件从模型的优化结果中提取所选取优化组合对应的每道工序的作业时间。优化组合(T，C，Q)=(106，608.97，0.83)所对应的每道工序的作业时间依次为(15，15，75，15，20，15，15，10，11，10，20，10，5)。工程管理人员可以以此为参考依据来对工程项目的各工序作业时间进行合理安排，以便于更好地开展接下来的项目管理工作。

在工程实际中，项目决策者对于工程各个目标的控制可能会有相应的目标及偏好。为此，可以为各个控制目标添加相应的约束条件以便更加准确地为项目管理者提供决策参考。此外，案例中选取的工程规模较小，而现实中大多数工程项目的工程规模将会庞大得多，项目也更为复杂，项目管理人员可以对大型工程项目进行相应地分解，从而使得模型更好地被运用。

总之，项目管理人员可以依据不同的工程实际情况对工期-成本-质量综合优化模型进行调整使用，从而最终提高模型的使用效率及效果。

4　结语

本文引入二元决策图(BDD)来对工程项目的整体质量水平进行评价，使得所构建的综合优化模型能够更加充分地考虑工程项目各工序之间的逻辑关系。同时，在前人研究成果的基础上，考虑工程实际对工期以及质量目标的奖罚制度，构建工期-成本-质量综合优化模型，并引入非支配近邻免疫算法(NNIA)来对所构建的综合优化模型进行求解。最后，通过一个工程实例对所模型和算法应用的可行性进行验证，利用MATLAB软件编程求解。运算结果得到了一系列Pareto最优解，从而为项目管理人员提供一定的决策依据。

此外，安全、环境等目标也是工程建设过程中需要考虑的重要指标，在之后的研究工作中可以将安全和环境等目标纳入工程多目标综合优化模型中，从而使得模型更加全面、准确。另外，在构建模型时设置了很多假设条件，未将资源供应情况、风险等影响因素考虑进去。今后的研究应在模型中多考虑项目目标的影响因素，使得模型更加贴合工程实际。

[1]BabuAJG,SureshN.Projectmanagementwithtime,cost,andqualityconsiderations[J].EuropeanJournalofOperationalResearch,1996,88(2):320-327

[2]El-RayesK,KandilA.Time-cost-qualitytrade-offanalysisforhighwayconstruction[J].JournalofConstructionEngineeringandManagement,2005, 131(4): 477-486

[3]Pollack-JohnsonB,LiberatoreMJ.Incorporatingqualityconsiderationsintoprojecttime/costtradeoffanalysisanddecisionmaking[J].IEEETransactionsonEngineeringManagement,2006,53(4):534-542

[4]张连营，岳岩.工期—成本—质量的模糊均衡优化及其Pareto解[J].同济大学学报(自然科学版),2013(02):303-308

[5]王健，刘尔烈，骆刚.工程项目管理中工期—成本—质量综合均衡优化[J].系统工程学报.2004(2):148-153

[6]杨耀红，汪应洛，王能民.工程项目工期成本质量模糊均衡优化研究[J].系统工程理论与实践,2006(7):112-117

[7]GhodsiR,SkandariMR,AllahverdilooM,etal.Anewpracticalmodeltotrade-offtime,cost,andqualityofaproject[J].AustralianJournalofBasicandAppliedSciences,2009,3(4):3741-3756

[8]AfsharA,KavehA,ShoghliOR.Multi-objectiveoptimizationoftime-cost-qualityusingmulti-colonyantalgorithm[J].AsianJournalofCivilEngineering(BuildingandHousing),2007,8(2):113-124

[9]RahimiM,IranmaneshH.Multiobjectiveparticleswarmoptimizationforadiscretetime,costandqualitytrade-offproblem[J].WorldAppliedSciencesJournal.2008,4(2):270-276

[10]刘吉成，常昊，王素花.基于Pareto蚁群算法的风电项目工期-成本-质量均衡优化[J].电力建设，2014(04):127-131

[11]赵瑞，刘晓君，申金山.建设项目多目标优化方法研究[J].西安建筑科技大学学报(自然科学版),2008,40(6):858-862

[12]武小悦，沙基昌.网络系统可靠度的BDD算法[J].系统工程与电子技术，1999(07):75-76

[13]GongM,JiaoL,DuH,etal.Multiobjectiveimmunealgorithmwithnondominatedneighbor-basedselection[J].EvolComput,2008,16(2):225-255

[14]雷德明.多目标智能优化算法及其应用[M].北京：科学出版社,2009

金成(1990.01-)，男，主要从事工程项目管理方面的工作。

Analysis of Time-cost-quality Trade-off Optimization In Engineering Project Based on Non-dominated Neighbor Immune Algorithm

JINCheng

(Shenzhen Oriental Ginza Group Co.,Ltd, Shenzhen 518040)

Project duration, cost and quality are three main objectives of engineering projects. The current controls of the three aspects are relatively independent, which produce the effect in practice is limited. In order to address the issue of coordination among the three objectives better and provide effective decision support for managers, a time-cost-quality trade-off model has been built. In addition the Non-dominated Neighbor Immune Algorithm (NNIA) has been used to solve the model. The computational result obtained a series of Pareto optimal solution, verifying the feasibility of the model and the effectiveness of NNIA to solve the model.

Engineering project; Time-Cost-Quality trade-off; Quality reliability; Non-dominated neighbor immune algorithm; Binary decision diagram

金成(1990. 1-)，男。

E-mail:sunnybanana@yeah.net

2016-01-23

TU71

A

1004-6135(2016)03-0084-05